算法基础——复杂度
前言
算法是解决问题的一系列操作的集合。著名的计算机科学家Niklaus Wirth曾提出:算法+数据结构=程序,由此可见算法在编程中的重要地位。本篇主要讨论算法性能好坏的标准之一——复杂度。
1 复杂度概述
1.1 什么是复杂度
本文所讨论的复杂度是指通过事先估算法计算出的用来衡量算法效率的值。因此并不是说代码的长度越长复杂度就越高,或者代码中的数据越多复杂度就越高。
1.2 为什么会有复杂度
关于复杂度的产生,我们通过下图的问题来引入。假设现在有一个人要从A地前往E地,那么他共有ABE、ADE、ABCE三种路径可以选择,但是我们可以看出,ABE的路程是最短的(假设图中距离与实际距离成比例),经过的地区也是最少的,相较于其它两条路径,ABE的优势非常明显。
算法是用来解决问题的操作步骤的集合,而我们解决同一个问题可能会如上例一样,有多种路径,这时我们需要一个标准来评判每条路径的好坏。这样一来,算法的复杂度就被提出了。
1.3 复杂度分类
算法的复杂度分为时间复杂度和空间复杂度两种。
时间复杂度用来衡量算法消耗时间的多少,空间复杂度用来衡量算法所需开辟新空间的多少。
2 时间复杂度
2.1 什么是时间复杂度
首先我们要明白,程序运行的绝对时间并不是衡量算法效率的标准。举个不太恰当的例子,使用“ENIAC”计算机(世界上第一台电子数字式计算机)与“天河一号”超级计算机执行相同的算法(死循环除外),它们的绝对时间必然有所不同。
从中我们得出,当我们评判一个算法的好坏时,不能附带有硬件条件的影响,而应关注算法本身。算法的执行时间的长度可以由每条语句的执行时间乘以该语句的执行次数,再加和得到。而每条语句的单次执行时间对现代计算机来说几乎可以忽略不计,那么对于一个程序的执行时间影响最大的因素就是单条语句的执行次数了。
因此,时间复杂度主要是用来渐进表示执行次数最多的单条语句的执行次数。
2.2 时间复杂度的计算
时间复杂度通常用"O"表示。对于任意输入量n(这里的输入量不一定是数字,也可能为数组或结构变量等,根据具体情况而定),算法的时间复杂度可记作"O(f(n))",其中f(n)为n的函数,表示算法中的语句的执行次数。但是我们通常会使用渐进表示法来表示时间复杂度,即取f(n)中次数最高的项来表示(当n足够大时,最高次项对整个数值的影响最大)。
如果仅仅通过这些文字来理解时间复杂度可能较为抽象,我们通过几个简单的例子来理解一下。
int main()
{int a;int i;for(i=0;i<10;i++)a=i;return 0;
}我们来看这段代码,这其中代码执行的总次数(即执行的语句数量)为13,为一个常数,我们计这段代码的时间复杂度为"O(1)"。
这可能与大家的理解有些偏差,明明执行次数为13,为什么不计作"O(13)"呢?我们来观察这段代码,由于这段代码的输入量n对程序的运行次数不会产生影响,那么无论输入量n的大小为多少,这段代码的执行次数都是13。当输入量n趋向于无穷大时,执行次数13与1的区别并不大,可以忽略不计。为方便起见,将这些执行次数为常数的算法的时间复杂度计为"O(1)"。
也就是说,无论算法的语句执行次数为10,20,30还是一亿,十亿,一百亿,只要它是常数,那么当输入量n趋向于无穷大时,这些常数均可忽略不计,则时间复杂度计为"O(1)"。
int main()
{int a;int n;int i;scanf("%d",&n);for(i=0;i<n;i++)a=i;return 0;
}我们再来看这段代码,这段代码与之前的代码相比的不同之处在于其有一个输入量n,并且输入量n会对代码的执行次数产生影响,例如,当输入2时,代码执行次数为7;输入量为10时,代码执行次数为15。可以推出,这段代码的执行次数与输入量n的关系为f(n)=n+5。
在这个关系中,当n趋向于无穷大时,5这个常量可忽略不计,因此我们将这个算法的时间复杂度计为"O(n)"。
通过对上面两段代码的分析,我们可以总结出一些规律,对比可以发现,影响时间复杂度的主要因素就是循环语句的循环次数与输入量n的关系。在第二段代码中,输入量为n时,循环语句执行n次,则时间复杂度为"O(n)"。
int main()
{int i,j,n;scanf("%d",&n);for(i=0;i<n;i++){for(j=0;j<n;j++){printf("%d ",i*j);}}while(i--){j--;}return 0;
}我们继续来看,这段代码中存在嵌套循环语句,当输入量为n时,对于任意一次外层循环,内层循环都进行n次。而外层循环也进行n次,因此总共可认为进行n*n次,即n^2。
除此之外,这段代码中还存在另一段while循环语句,不难得出循环进行n次,因此这段代码执行的总次数可以计为n^2+n+2。当输入量n趋向于无穷大时,相对于n^2,n+2的值对总次数的影响并不大,可以忽略不计。
因此,这段代码的时间复杂度计为"O(n^2)"。
2.3 一些经典算法的时间复杂度分析
2.3.1 冒泡排序
冒泡排序是一种简单的交换排序,通过比较相邻两个元素的大小,若它们的大小顺序与所需顺序不同,则交换这两个元素。这里先不讨论冒泡排序的原理,直接来分析代码。
void BubbleSort(int* a,int sz)
{int i,j;for(i=0;i<sz-1;i++) //排序次数{for(j=0;j<sz-i-1;j++) //比较次数{if(arr[j]<arr[j+1]) //判断相邻两数据大小{int tmp = arr[j];arr[j] = arr[j+1];arr[j+1] = tmp;}}}
}上面为一段最简单的冒泡排序算法,其中参数a为所需排序的数组的地址,sz为所需排序的元素个数,当给定数组大小为n时,该算法的循环总共进行[(n-1)+(n-2)+...+1]次,化简可得(n^2-n)/2次,因此该算法的时间复杂度计为"O(n^2)"。
2.3.2 二分查找
二分查找是一种非常高效的查找算法,可以在一串有序数据中快速查找出所需数据。
int BinarySearch(int* a,int sz,int x)
{int left=0,right = sz-1;while(left<=right){int mid = (left+right)/2; //取中间值if(a[mid] == x) return mid; //找到与x相等的元素,返回下标else if(x > a[mid])left = mid; //中间值偏小elseright = mid; //中间值偏大}return -1; //查找失败
}二分查找算法的最好情况是第一次就找到目标值,此时时间复杂度为"O(1)"。但是我们评判一个算法的好坏不可能凭其处理问题的最好情况时的复杂度作为参考,这是没有意义的。一般来讲,我们会以算法的处理最坏情况的时间复杂度作为该算法的时间复杂度。
在最坏的情况下,在整个数组中无法找到目标元素。由于二分查找每次取中间值即可排除一半的元素,因此可得当输入量为n时,二分查找总共需要进行大约为以二为底n的对数次,当对数的底数为2时,在表示算法的时间复杂度时,可计为"O(logn)"。
因此,二分查找的时间复杂度为"O(logn)"。
3 空间复杂度
3.1 什么是空间复杂度
我们知道,程序运行时需要调用内存空间,而算法作为程序的一部分,同样也需要调用空间。
而空间复杂度就是衡量一个算法执行所需调用空间的大小的标准。
在很多情况下,在评判算法的性能好坏时,空间复杂度的参考权重比时间复杂度要低得多,因此有些算法可能会采取牺牲空间复杂度的方式来换取更低的时间复杂度。但这并不代表空间复杂度不重要。
3.2 空间复杂度的计算
空间复杂度的计算和时间复杂度的计算较为相似,在理解了时间复杂度的计算规则后,理解空间复杂度的计算应该会比较轻松。我们还是通过例子来分析。
int main()
{int a;return 0;
}上面这段代码可以说非常简单了,总共开辟了两块内存空间,一块用来调用main函数,另一块存储变量a。由于开辟的空间大小为常数,因此该段代码的空间复杂度为"O(1)"。
int* copy(int* a,int sz)
{int* ret = (int*)malloc(sizeof(int)*sz);return ret;
}这是一个复制函数,用来将给定的数组复制。在这个函数中,当给定数组的大小为n时,该函数会开辟一个大小为n的空间用来复制数组,因此其空间复杂度为"O(n)"。
结束语
了解复杂度是学习算法的基础,它让我们明白如何判断一个算法的好坏。学会判断复杂度后,我们将会知道如何优化算法,并学会在不同情景下使用最合适的算法。
以上就是我对复杂度的理解了,如内容有误欢迎各位大佬指正。
相关文章:

算法基础——复杂度
前言 算法是解决问题的一系列操作的集合。著名的计算机科学家Niklaus Wirth曾提出:算法数据结构程序,由此可见算法在编程中的重要地位。本篇主要讨论算法性能好坏的标准之一——复杂度。 1 复杂度概述 1.1 什么是复杂度 本文所讨论的复杂度是指通过事先…...

基类与派生类对象的关系 派生类的构造函数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
【算法】生成分布式 ID 的雪花算法
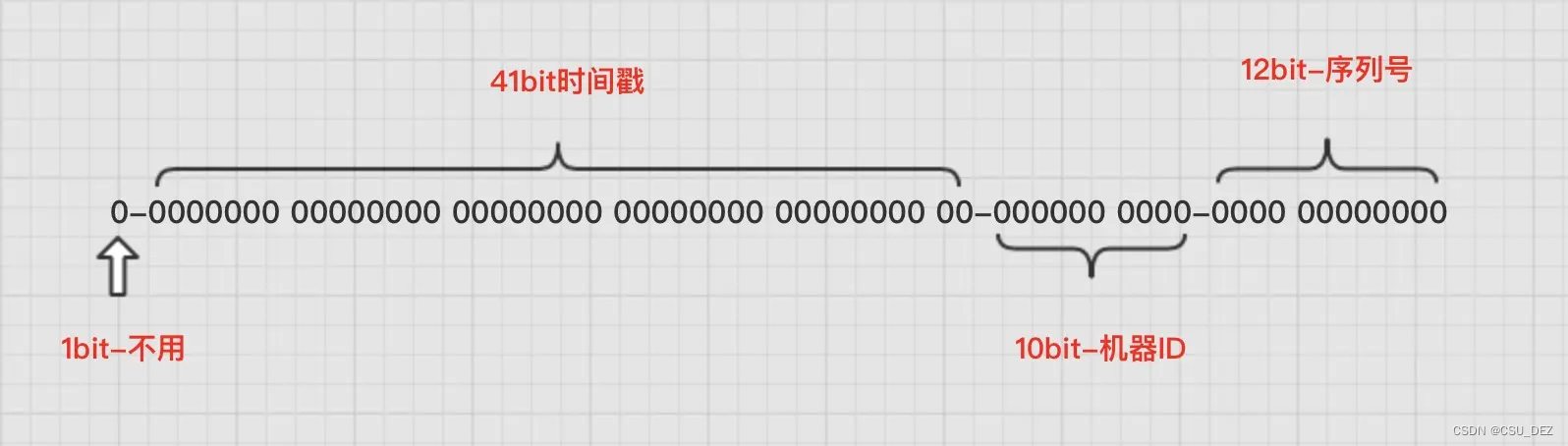
ID 是数据的唯一、不变且不重复的标识,在查询数据库的数据时必须通过 ID 查询,在分布式环境下生成全局唯一的 ID 是一个重要问题。 雪花算法(snowflake)是一种生成分布式环境下全局唯一 ID 的算法,该算法由 Twitter 发…...
Linux系统编程 - 基础IO(IO操作)
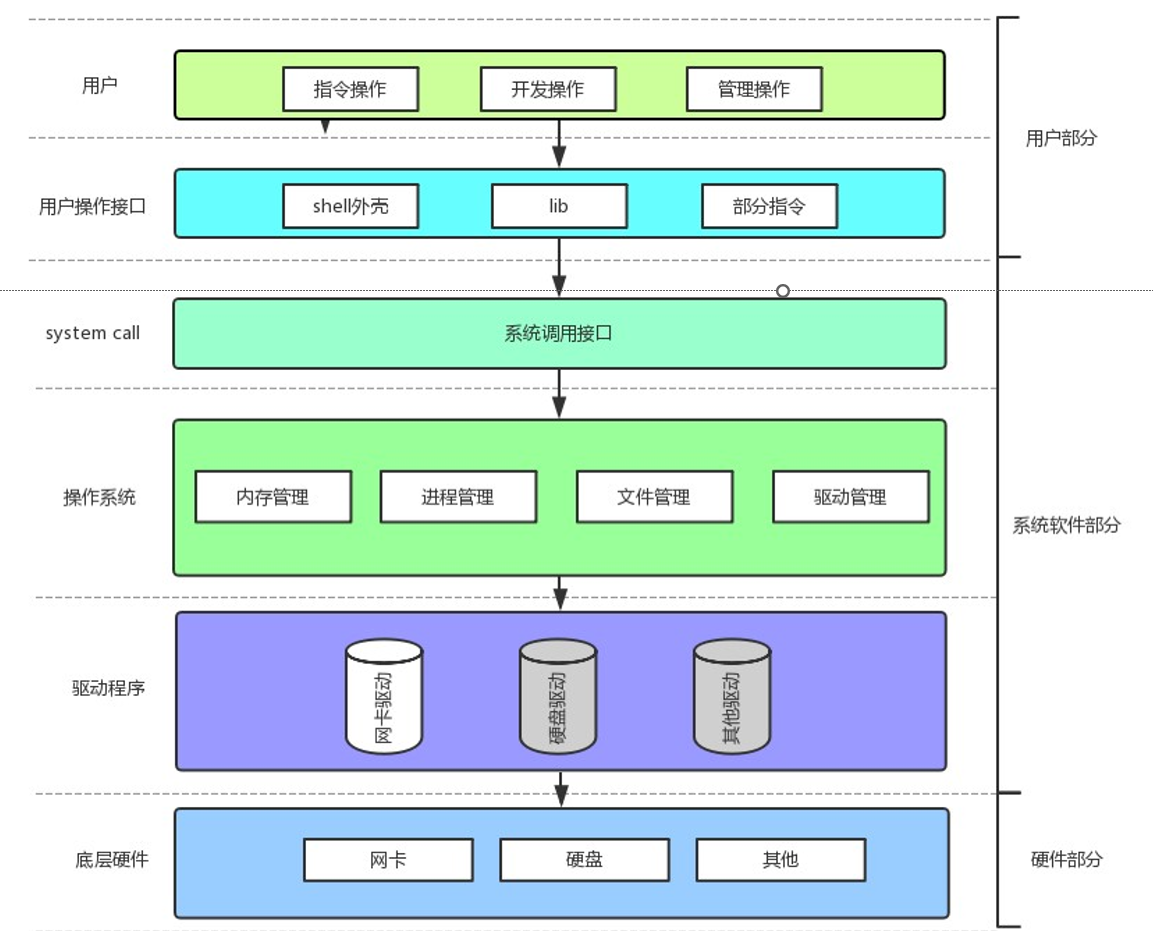
目录 预备知识 复习C文件IO相关操作 printf相关函数 fprintf snprintf 读取文件 系统文件IO操作 open函数 umask()函数 open函数返回值 预备知识 1.你真的理解文件原理和操作了吗?不是语言问题,是系统问题2.是不是只有C/C有文件操作呢&#x…...

基于 Avue 的 CRUD 表格组件封装
在 components 文件夹中,创建一个新的 .vue 文件,例如:AvueCrudTable.vue。 透传父组件传递的属性和事件 : 1、利用v-bind=“ a t t r s " 支持所有 a v u e 的使用方法并在其基础上进行封装 2 、使用 v − o n = " attrs"支持所有 avue 的使用方法并在其基…...
基于框架编写驱动代码)
树莓派学习笔记(十三)基于框架编写驱动代码
文章目录一、代码分析:二、源码一、代码分析: 在内核中由于代码文件多,避免函数名重复,使用static将函数的作用域限制在该文件内 内核的打印函数printk和printf类似 file_operations结构体使用符号“ . ”指定参数,省…...
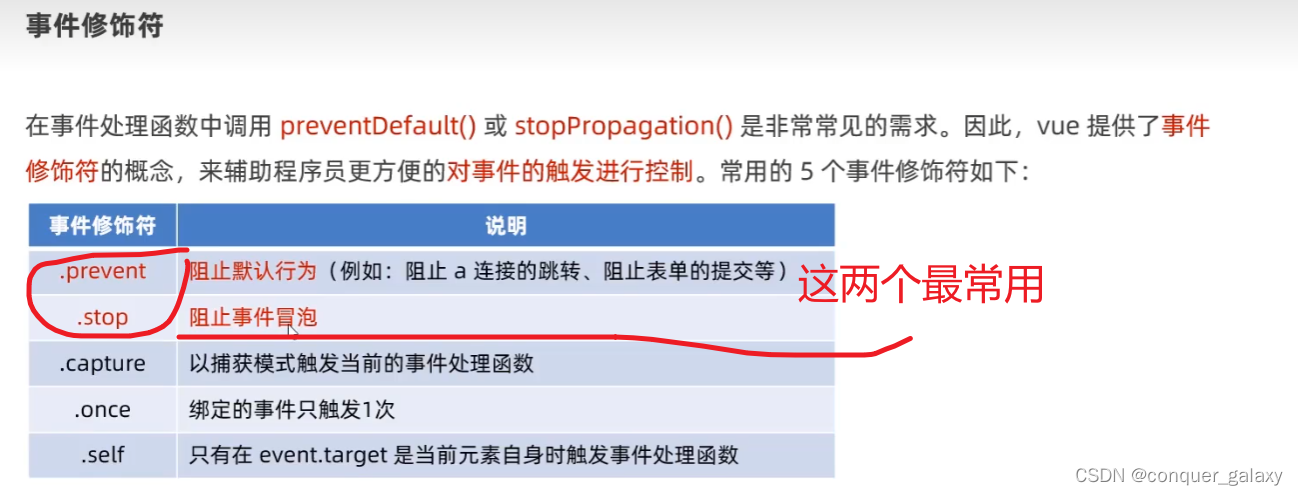
vue事件修饰符之.prevent
.prevent 事件修饰符只是阻止默认事件,不会自动触发任何事件处理函数。因此,在使用 .prevent 事件修饰符时,需要自己编写相应的事件处理函数来处理事件。 例如,在上面的例子中,我们通过在表单上绑定 submit.prevent&q…...

【SpringCloud AlibabaSentinel实现熔断与限流】
本笔记内容为尚硅谷SpringCloud AlibabaSentinel部分 目录 一、Sentinel 1、官网 2、Sentinel是什么 3、下载 4、特性 5、使用 二、安装Sentinel控制台 1、sentinel组件由2部分构成 2、安装步骤 1.下载 2.运行命令 3.访问sentinel管理界面 三、初始化演示工程 …...

类与对象-封装
一、封装的意义封装是C面向对象三大特性之一语法: class name { 访问权限:属性行为 };注意:类中的属性和行为 统称为成员属性 又称 成员属性 / 成员变量行为 又称 成员函数 / 成员方法封装将属性和行为作为一个整体,表现生活中的事物例①&…...

【回忆杀】2012年拥有第一台电脑【致逝去的青春】
高中说起 在2012年的时候吧,高考过后,那个时候一门心思的想当一名体育老师【现在居然还有这个想法,哈哈】,最后没有考上自己希望的大学我记得好像是2012年7月的时候就去重庆投靠朋友,他教我做模具,2012年做…...

PointNeXt: Revisiting PointNet++ with Improved Training and Scaling Strategies
Abstract PointNet 是点云理解领域最有影响力的神经网络架构之一。虽然近期出现了 PointMLP 和 Point Transformer 等新型网络,它们的精度已经大大超过了 PointNet,但我们发现大部分性能提升是由于改进的训练策略,例如数据增强和优化技术以及…...
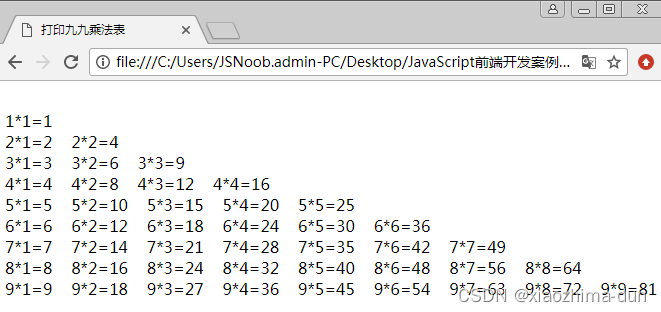
打印九九乘法表-课后程序(JavaScript前端开发案例教程-黑马程序员编著-第2章-课后作业)
【案例2-9】打印九九乘法表 一、案例描述 考核知识点 for双重循环 练习目标 掌握for循环应用。实现九九乘法表。 需求分析 九九乘法表相信大家一点也不陌生,之前见到的乘法表是印刷在课程本之上的。而在本案例中我们将用JavaScript代码来实现九九乘法表。 案例分…...
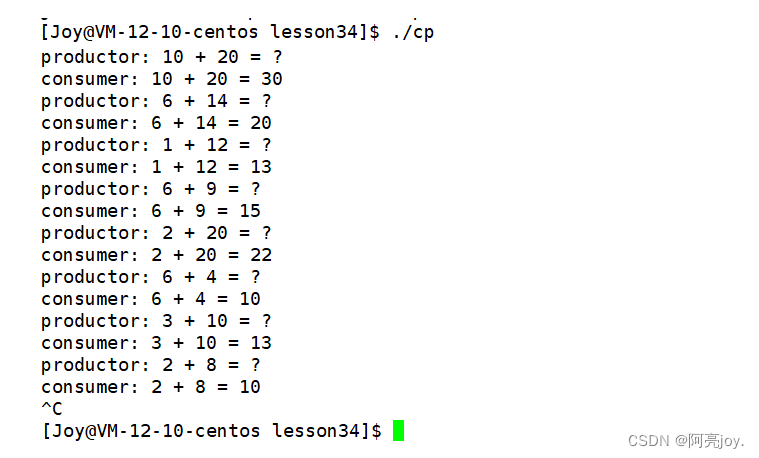
【Linux】基于阻塞队列的生产者消费者模型
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉为何要使用…...
)
【华为OD机试 2023最新 】 真正的密码(C++)
文章目录 题目描述输入描述输出描述用例题目解析C++题目描述 在一行中输入一个字符串数组,如果其中一个字符串的所有以索引0开头的子串在数组中都有,那么这个字符串就是潜在密码, 在所有潜在密码中最长的是真正的密码,如果有多个长度相同的真正的密码,那么取字典序最大的…...
)
差分算法(蓝桥杯复习+例题讲解+模板c++)
文章目录差分介绍差分应用区间加区间求和总结3729. 改变数组元素100. 增减序列文章首发于:My Blog 欢迎大佬们前来逛逛 差分介绍 差分是一种常见的算法,用于快速修改数组中某一段区间的值。 差分的思想就是预处理出数组的差分数组,然后修改…...

CSS+ JS 实现手电筒效果
前言概述 JavaScript 结合 CSS 打造的一款图片特效,当鼠标拖拽滑块时,让本该置灰的图片局部恢复本来的颜色。且该效果随着你的鼠标的按下时的移动而移动。 核心功能 图片置灰 拖拽功能 让滑块位置处的图片恢复本来的颜色 实现原理 这个的实现原理并不…...

2021地理设计组二等奖:基于InSAR和指数分析的地面沉降风
作品简介 一、作品背景 地面沉降是指地面高程的降低, 又称地面下沉或地沉, 是以缓慢、难以察觉的向下垂直运动为主, 是指在自然和人为因素作用下, 由于地壳表层土体压缩而导致区域性地面标高降低的一种环境现象。目前, 地面沉降己成为城市化进程中普遍存在的生态环境问题, 成为…...
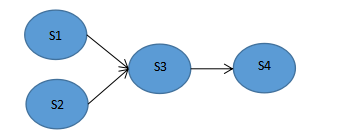
计算机操作系统(第四版)第二章进程的描述与控制—课后习题答案
1.什么是前趋图?为什么要引入前趋图? 前趋图是一个有向无循环图,记为DAG,用于描述进程之间执行的先后关系。 2.试画出下面四条语句的前趋图: S1:axy; S2:bz1; S3:ca-b; S4:wc1; 3.为什么程序并发执行会产生间断性特征&…...
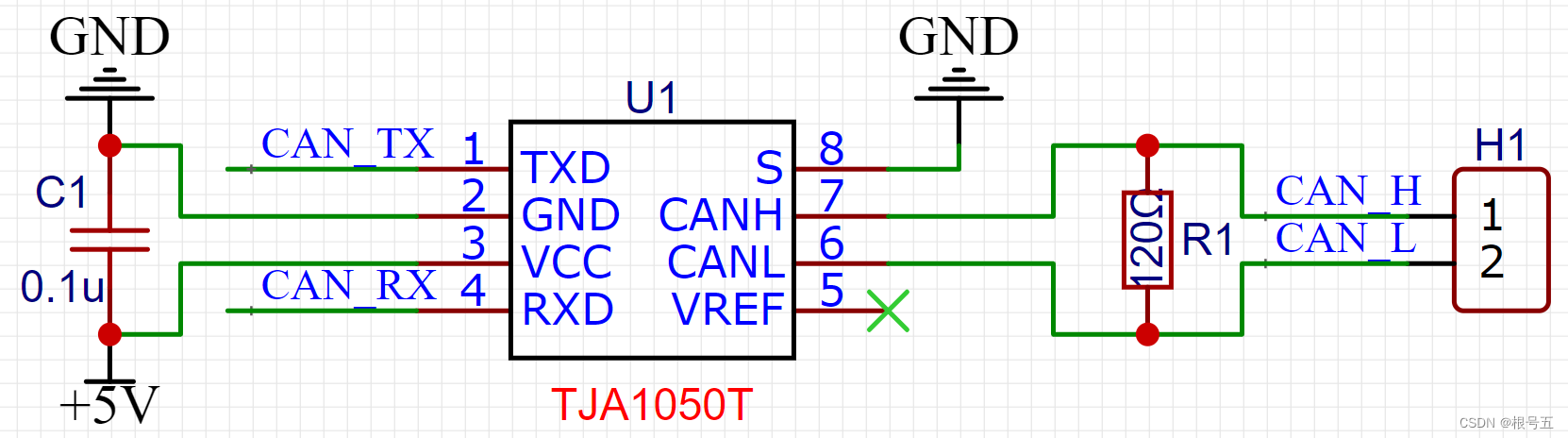
CAN通信----电路图
CAN通信----基本原理 一、CAN总线网络连接 1.闭环总线网络----ISO11898 闭环总线网络高速、短距离,它的总线最大长度为 40m,通信速度最高为 1Mbps,总线的两端各要求有一个120 欧的电阻。 2.开环总线网络----ISO11519 开环总线网络低速、…...

Windows系统安装ElasticSearch(一)
一 ES介绍Elasticsearch 是一个分布式可扩展的实时搜索和分析引擎,一个建立在全文搜索引擎 Apache Lucene(TM) 基础上的搜索引擎.当然 Elasticsearch 并不仅仅是 Lucene 那么简单,它不仅包括了全文搜索功能,还可以进行以下工作:分布式实时文件存储&#…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
