差分算法(蓝桥杯复习+例题讲解+模板c++)
文章目录
- 差分介绍
- 差分应用
- 区间加
- 区间求和
- 总结
- 3729. 改变数组元素
- 100. 增减序列
文章首发于:My Blog 欢迎大佬们前来逛逛
差分介绍
差分是一种常见的算法,用于快速修改数组中某一段区间的值。
差分的思想就是预处理出数组的差分数组,然后修改区间时,只需要修改两个位置的值,即可快速完成区间修改。最后再通过差分数组求出原数组。 差分数组 did_idi 表示原数组中相邻两个元素之间的差值,即 di=ai−ai−1d_i=a_i-a_{i-1}di=ai−ai−1,其中 aia_iai 表示原数组中第 iii 个元素的值。则对于区间 [l,r][l,r][l,r] 的加上 kkk 的操作,可以表示为: dl=dl+k,dr+1=dr+1−kd_l=d_l+k,\quad d_{r+1}=d_{r+1}-kdl=dl+k,dr+1=dr+1−k 这样就完成了区间加 kkk 的操作。最后只需要用差分数组求出原数组即可。 ai=∑j=1idja_i=\sum_{j=1}^{i} d_jai=j=1∑idj
差分应用
区间加
以区间加为例,设 aia_iai 表示原数组中第 iii 个元素的值,did_idi 表示差分数组中第 iii 个元素的值,则对于区间 [l,r][l,r][l,r] 的加上 kkk 的操作,可以表示为: dl=dl+k,dr+1=dr+1−kd_l=d_l+k,\quad d_{r+1}=d_{r+1}-kdl=dl+k,dr+1=dr+1−k 最后只需要用差分数组求出原数组即可: ai=∑j=1idja_i=\sum_{j=1}^{i} d_jai=j=1∑idj 以下是区间加的代码实现:
vector<int> a; // 原数组
vector<int> d(a.size(), 0); // 差分数组
// 区间加 k
int l = 2, r = 5, k = 3;
d[l] += k;
d[r+1] -= k;
// 求出原数组
for (int i = 1; i < a.size(); i++) {d[i] += d[i-1];
}
区间求和
另一种常见的操作是区间求和。设 aia_iai 表示原数组中第 iii 个元素的值,did_idi 表示差分数组中第 iii 个元素的值,则对于区间 [l,r][l,r][l,r] 的求和操作,可以表示为: ∑i=lrai=∑i=lr(∑j=1idj)=∑j=1rdj−∑j=1l−1dj\sum_{i=l}^{r} a_i = \sum_{i=l}^{r} (\sum_{j=1}^{i} d_j) = \sum_{j=1}^{r} d_j - \sum_{j=1}^{l-1} d_ji=l∑rai=i=l∑r(j=1∑idj)=j=1∑rdj−j=1∑l−1dj 这样就能用差分数组快速求出区间和了。 以下是区间求和的代码实现:
cppCopy codevector<int> a; // 原数组
vector<int> d(a.size(), 0); // 差分数组
// 区间加 k
int l = 2, r = 5, k = 3;
d[l] += k;
d[r+1] -= k;
// 求出原数组
for (int i = 1; i < a.size(); i++) {d[i] += d[i-1];
}
// 区间求和
l = 3, r = 7;
int ans = d[r] - d[l-1];
总结
差分是一种常见的算法,用于快速修改数组中某一段区间的值。差分的思想就是预处理出数组的差分数组,然后修改区间时,只需要修改两个位置的值,即可快速完成区间修改。最后再通过差分数组求出原数组。差分算法在区间加、区间求和等问题中都有广泛的应用。
3729. 改变数组元素
3729. 改变数组元素
题目要求:初始给你一个全为0的序列,给你一组数据,其中每一个数组a[i]=n表示对自 i 开始的的前面n个元素全都都变为1,已经是1的不予理会,求得操作完成后的数列的值。
示例:
6
0 3 0 0 1 3
操作后:
1 1 0 1 1 1
对于【2】位置,它的值为3,意味着自位置 2开始,前3个元素全部都变为1,则:
差分数组:[0]=1,[3]=-1。
我们根据差分数组转换为原数组:1到3的元素就是 1 1 0,这样我们就成功的利用差分数组改变了原数组的值。
因此对于每一个位置的值,我们对差分进行操作,b[l]+=1,b[r]-=1,最后利用差分数组转换为原数组。
注意几个地方:
- 如果根据所给的值得到对差分数组操作的 l 与r? 假设我们的值为x,则左端点为 i-x+1,右端点为 i
- x必须取 i 和 x 的最小者,原因是即使 x大于i,则 i-x会得到一个负值,我们使得x=i,那么这样的话就是默认左端点为1开始
- 只需对差分数组进行操作:b[l]+=1,b[r]-=1
- 根据差分数组反推出原数组
- 我们只需要得到每一个位置的值是0还是1即可,对于原数组我们根据其值进行两次 !!的操作,这个操作可以使得 0值仍然是0值,任意非零值都是1
- 注意清空差分数组的元素值。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
using namespace std;
const int N=2e5+10;
int nums[N],b[N];
int t,n;
int main(){cin>>t;while (t--){cin>>n;memset(b,0,(n+1)*4);for (int i=1;i<=n;i++){int x;cin>>x;x=min(x,i);int l=i-x+1,r=i;b[l]+=1;b[r+1]-=1;}for (int i=1;i<=n;i++){b[i]+=b[i-1];}for (int i=1;i<=n;i++){cout<<!!b[i]<<' ';}cout<<endl;}return 0;
}
100. 增减序列
100. 增减序列 - AcWing题库
题目要求:每次对某个区间进行操作可以选择整体加1,或者整体减1,使得整个数列的值全部相等,求得最少操作次数与最少操作次数对应的整个数列值的不同方案。
4
1 1 2 2
操作后得:
1 1 1 1
2 2 2 2
-----
0 0 0 0 //非最少操作次数,因此不计
最少操作次数为2,即我们把 1到2的1整体加1,即可得到全部为2;把3到4的2整体减1,可以得到全部为1,这两种操作的最少操作次数都是1次,对应的方案数有两种
如果我们要想把全部的数列的值都变为唯一的值,则它对应的差分数组的值一定是:
num 0 0 0 0...
即b[1]=num,往后每一个 b的值都为0,这样我们就得到了一个全部值都相同的原数组。
因此我们该如何构造一个这样的差分数组呢?
- 只有首元素不为零
- 差分数组中 2到n的全部元素都为0
可以发现:
-
最少操作次数:把差分数组变为上面的情况的最少操作次数
-
对应的方案数:因此就是求 b[1] 有多少种方案,就是数列中不同的值的种类
则在区间【2,n】中:
由于差分数组中值有正有负,因此我们根据贪心的思路:
每次选择两个符号不同的数值,一个加1,一个减1,这样就能用最少的次数将正负两个符号不同的数字相消
我们规定pos为差分数组中所有正数的和,neg为所有负数的绝对值的和。
则min(pos,neg)就是正数与负数进行相消的方案数,然后使得数列中所有的值都是相同符号:
假设差分数组为:
2 5 -2 3 -1
pos=8,neg=3,则我们经过 min(8,3)=3,即经过了三次操作使得所有的负数都消失:
2 3 0 2 0 (两个负数一个加2,一个加1,对应其他位置一个减2,一个减1)
然后我们得到了全部都是符号相同的序列,下一步我们就是把【2,n】中所有的符号相同的数相消,使得数列中只留下【1】位置的值,则对于【2,n】中的数字可以有两种方案进行相消:
- 与【1】位置的值进行相消,此时会改变【1】的值
- 与【n+1】位置的值进行相消,此时不会改变【1】的值,【n+1】位置的值无意义。
因此我们再经过 |pos-neg|次操作使得所有的【2,n】位置的元素全部变为0,对于最少操作次数,选择两种方案都是一样的,因此最少操作次数为:min(pos,neg)+abs(pos-neg)
如果要统计对应的最少操作次数的方案数:则一定是 |pos-neg|+1。
上面相同符号进行相消配对的时候,选择 |pos-neg| 个与[1]匹配,则[1]改变,可以造成|pos-neg|个[1]的不同情况;另外选择[n+1],则[1]不变,可以造成1种[1]的情况。
因此最终的组合数就是 |pos-neg|+1
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
using namespace std;
#define int long long
const int N=1e5+10;
int nums[N];
int n;
signed main(){cin>>n;for (int i=1;i<=n;i++){cin>>nums[i];}for (int i=n;i>1;i--){nums[i]-=nums[i-1];}int pos=0,neg=0;for (int i=2;i<=n;i++){if (nums[i]>0) pos+=nums[i];else neg-=nums[i];}cout<<min(pos,neg)+abs(pos-neg)<<endl;cout<<abs(pos-neg)+1<<endl;return 0;
}
相关文章:
)
差分算法(蓝桥杯复习+例题讲解+模板c++)
文章目录差分介绍差分应用区间加区间求和总结3729. 改变数组元素100. 增减序列文章首发于:My Blog 欢迎大佬们前来逛逛 差分介绍 差分是一种常见的算法,用于快速修改数组中某一段区间的值。 差分的思想就是预处理出数组的差分数组,然后修改…...

CSS+ JS 实现手电筒效果
前言概述 JavaScript 结合 CSS 打造的一款图片特效,当鼠标拖拽滑块时,让本该置灰的图片局部恢复本来的颜色。且该效果随着你的鼠标的按下时的移动而移动。 核心功能 图片置灰 拖拽功能 让滑块位置处的图片恢复本来的颜色 实现原理 这个的实现原理并不…...

2021地理设计组二等奖:基于InSAR和指数分析的地面沉降风
作品简介 一、作品背景 地面沉降是指地面高程的降低, 又称地面下沉或地沉, 是以缓慢、难以察觉的向下垂直运动为主, 是指在自然和人为因素作用下, 由于地壳表层土体压缩而导致区域性地面标高降低的一种环境现象。目前, 地面沉降己成为城市化进程中普遍存在的生态环境问题, 成为…...
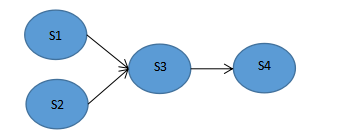
计算机操作系统(第四版)第二章进程的描述与控制—课后习题答案
1.什么是前趋图?为什么要引入前趋图? 前趋图是一个有向无循环图,记为DAG,用于描述进程之间执行的先后关系。 2.试画出下面四条语句的前趋图: S1:axy; S2:bz1; S3:ca-b; S4:wc1; 3.为什么程序并发执行会产生间断性特征&…...
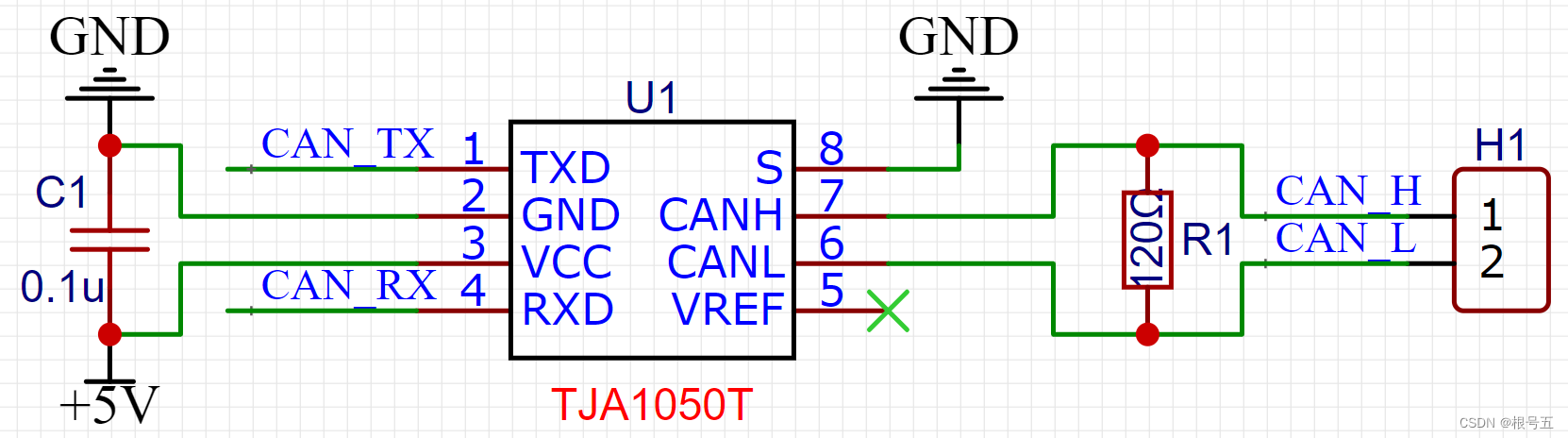
CAN通信----电路图
CAN通信----基本原理 一、CAN总线网络连接 1.闭环总线网络----ISO11898 闭环总线网络高速、短距离,它的总线最大长度为 40m,通信速度最高为 1Mbps,总线的两端各要求有一个120 欧的电阻。 2.开环总线网络----ISO11519 开环总线网络低速、…...

Windows系统安装ElasticSearch(一)
一 ES介绍Elasticsearch 是一个分布式可扩展的实时搜索和分析引擎,一个建立在全文搜索引擎 Apache Lucene(TM) 基础上的搜索引擎.当然 Elasticsearch 并不仅仅是 Lucene 那么简单,它不仅包括了全文搜索功能,还可以进行以下工作:分布式实时文件存储&#…...

linux 产生随机数 并遍历
1、产生随机数 varRANDOMvarRANDOM varRANDOMvar[ $var % 150 ] 2、产生不重复的随机数 $ entries($(shuf -i 0-149 -n 15)) $ echo “${entries[]}” 3、对随机数排序 $ entries($(shuf -i 0-149 -n 15 | sort -n)) $ echo “entries[]"12224549546678798393118119124140…...

【3.24】Mybatis常见面试题
Mybatis常见面试题 #{}和¥{}的区别是什么? 【#】:底层执行SQL使用PreparedStatement对象,预编译SQL,相对安全。入参使用占位符的方式。 【$】:底层执行SQL使用Statement对象,入参使用SQL拼接的…...
IDEA 热部署,修改代码不用重启项目
热部署指在修改项目代码的时候不重启服务器让修改生效。安装JRebel and XRebelFile->Settings,然后Plugins-> Marketplace,输入JRebel,安装如下插件——JRebel and XRebel ,重启idea激活JRebel and XRebel第一行输入网址&am…...
将 XLS 转换为 EXE:xlCompiler Crack
只需单击几下即可将Excel文件转换为应用程序 xl编译器无需编程即可将您的Excel电子表格转换为软件应用程序 将 XLS 转换为 EXE 将Excel文件转换为具有保护选项的应用程序。Excel 到 EXE 转换器为您提供了分发 Excel 模型的竞争优势和灵活性。将 Excel 的功能丰富的环境保存在应…...
【百面成神】spring基础12问,你能坚持到第几问
前 言 🍉 作者简介:半旧518,长跑型选手,立志坚持写10年博客,专注于java后端 ☕专栏简介:java面试宝典,特点:全、精、深、简,力求每个核心知识点1分钟回答好。 dz…...
javaSE类和对象(下)
目录君1.封装2.访问限定符3.包的定义及使用4.static成员变量5.static成员方法6.代码块及其分类实例代码块静态代码块静态代码块与实例代码块的执行顺序static成员变量(类变量)初始化1.封装 面向对象程序三大特性:封装、继承、多态。而类和对象阶段,主要…...

【数据结构】第四站:单链表力扣题(二)
目录 一、链表的回文结构 二、相交链表 三、环形链表 四、环形链表Ⅱ 五、复制带随机指针的链表 一、链表的回文结构 题目描述:链表的回文结构_牛客题霸_牛客网 对于这道题,如果没有前面的一些题的基础,是非常难做的,我们的思…...

KafKa知识汇总
前言 汇总相关知识 Kafka快速实战与基本原理详解...

【RV1126】调试GT911,1024x600 7寸 MIPI 电容触摸屏
文章目录一、驱动注册失败二、触摸屏可以触摸,但是x轴数据反了三、可以触摸了,但是Y轴数据跳变,几乎只有一半的屏幕是可以正常滑动的三、汇顶触摸屏配置文件解析四、使用新的配置文件4.1 新配置解决问题4.2 测试触摸的方法在kernel增加frame …...
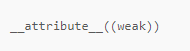
C的强符号/弱符号
首先上代码和结果: 代码: #include <stdio.h> int k; int k; int main() {printf("addr of k %p\n", &k);printf("value of k %d\n", k);return 0; }结果: addr of k 00408074 value of k 0问题&…...
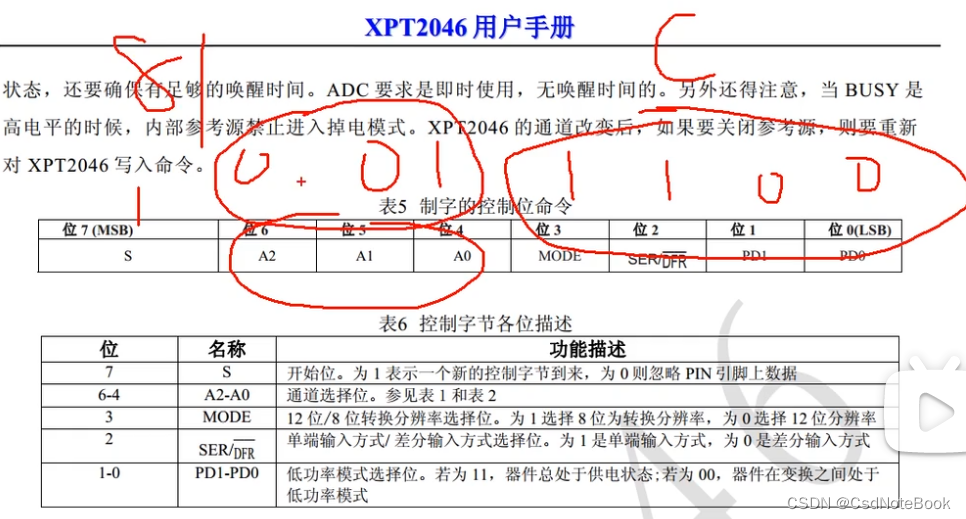
AD/DA转换(XPT2046)
AD/DA介绍AD(Analog to Digital):模拟-数字转换,将模拟信号转换为计算机可操作的数字信号DA(Digital to Analog):数字-模拟转换,将计算机输出的数字信号转换为模拟信号AD/DA转换打开…...

乐观锁和悲观锁 面试题
Mysql的乐观锁和悲观锁 实现方式加锁时机常见的调用方式优势不足适用场景乐观锁开发自定义更新数据的时候sql语句中进行version的判断高并发容易出现不一致的问题高并发读,少写悲观锁Mysql内置查询数据的开始select * for update保证一致性低并发互联网高并发场景极…...
【Autoware规控】mpc_follower模型预测控制节点
文章目录1. 技术原理2. 代码实现1. 技术原理 MPC,即Model Predictive Control(模型预测控制),是一种基于动态模型的控制算法。MPC算法通过建立系统的数学模型,根据当前状态和一定时间内的预测,优化未来的控…...

成果VR虚拟3D展厅让内容更丰富饱满
随着数字技术的不断发展和普及,数字化展厅成为了一种重要的展示形式。线上虚拟展厅作为数字化展示的一种新形式,采用虚拟现实技术,能够克服时空限制,打破传统展览业的展示模式,为用户提供更加丰富、立体、沉浸式的展览…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
