java编程 斐波拉契数列算法集锦【斐波拉契数列】【下】【集合类】【Stream函数式编程】
斐波那契数列(Fibonacci sequence),又称黄金分割数列,是一个非常经典的递归问题。斐波那契数列的算法描述:

斐波那契数列,一个令人着迷而又充满神秘色彩的数字序列,它以0和1作为起始,后续的每一个数字都是前两个数字的和。这个看似简单的数列,却蕴藏着自然界中无数令人惊叹的奥秘。

在自然界中,斐波那契数列无处不在,它像是一个隐形的脉络,贯穿于万物生长的每一个细节之中。你是否注意到,菠萝的果鳞排列呈现出一种特定的规律?那就是斐波那契数列!再看向日葵的种子排列,同样是斐波那契数列的完美展现。这种数列不仅在植物中有所体现,动物界也同样留下了它的足迹。比如,鹦鹉螺的螺旋生长模式,就是斐波那契数列在三维空间中的绝佳例证。下图左边图形是斐波那契数列互相镜像的螺旋线。

上一篇博客:java编程 斐波拉契数列算法集锦【斐波拉契数列】【上】
好了言归正传,上一篇博客我们已经介绍了不少斐波拉契数列的算法,本文我们再来补充一点。
- 算法7:利用集合框架中的Map实现斐波拉契数列的算法。
这个算法版本利用 Map 的 computeIfAbsent() 方法高效计算斐波那契数列。避免对较小的序列的重复计算。这个算法版本的思想其实与上一篇博客中【算法4: 借助一个数组列表ArrayList,前两项是0和1,从n=2项起,每一项是之前两项之和。实际上也是一种迭代算法】相似。所谓的高效是针对于上篇博客【算法1: 斐波那契数列的递归算法版本】而言的,因为这个算法在计算数列后面的项时需要多次重复计算前面所有的项。
package fibonacci;
/**** @author QiuGen* @description 斐波那契数列的递归算法* *** 使用 Map 的 computeIfAbsent() 方法高效计算* *** 斐波那契数列。避免对较小的序列的重复计算。* @date 2024/8/20* ***/
import java.util.HashMap;
import java.util.Map;
/*** 使用 Map 的 computeIfAbsent() 方法高效计算* 斐波那契数列。避免对较小的序列的重复计算。***/
public class FibonacciMap {private final Map<Integer,Long> map;public FibonacciMap() {map = new HashMap<>();map.put(0, 0L);map.put(1, 1L);} public long addValue(int x) {return map.computeIfAbsent(x, k -> addValue(k-1) + addValue(k-2));} public void printMap() {map.forEach((k,v)->System.out.println(v));}public static void main(String[] args) {System.out.println("***利用集合computeIfAbsent方法的递归算法***");FibonacciMap fibonacci = new FibonacciMap();for (int i = 0; i < 20; i++) {fibonacci.addValue(i);}fibonacci.printMap();}
}例程测试结果。例程的前20项结果,也是一样的:

- 算法8:函数式编程实现斐波拉契数列算法
首先迭代生成一个包含斐波拉契数列的两项元素Stream<long[]>流
/***迭代生成斐波那契数列的无限流***/public static Stream<long[]> fibStream( ) {Stream<long[]> fibStream = Stream.iterate(new long[]{0, 1},fib -> new long[]{fib[1], fib[0] + fib[1]});return fibStream;}
用Collect收集结果,结果保存在List列表中,然后遍历打印结果。
/**用Collect收集结果**/public static void fibStreamA( ) {List<Long> lst = fibStream().map(fib -> fib[0]).limit(30) //前30项.collect(ArrayList::new, ArrayList::add,ArrayList::addAll);lst.forEach(System.out::println);}
- 算法9:函数式编程转换为LongStream用forEach打印结果的算法
前面部分产生Stream<long[]>流与算法8相同。
然后,转换为LongStream用forEach打印结果。
/**转换为LongStream用forEach打印结果**/public static void fibStreamB( ) {LongStream fibLongStream = fibStream().map(fib -> fib[0]).mapToLong(k->k).limit(30); //前30项fibLongStream.forEach(System.out::println);}
最后,是算法8和算法9,函数式编程实现斐波拉契数列算法的测试程序的完整源码:
package fibonacci;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.LongStream;
import java.util.stream.Stream;/**** @author QiuGen* @description 斐波那契数列的函数式编程的算法* @date 2024/8/20* ***/
public class FibonacciStream {/***迭代生成斐波那契数列的无限流***/public static Stream<long[]> fibStream( ) {Stream<long[]> fibStream = Stream.iterate(new long[]{0, 1},fib -> new long[]{fib[1], fib[0] + fib[1]});return fibStream;}/**用Collect收集结果**/public static void fibStreamA( ) {List<Long> lst = fibStream().map(fib -> fib[0]).limit(30) //前30项.collect(ArrayList::new, ArrayList::add,ArrayList::addAll);lst.forEach(System.out::println);}/**转换为LongStream用forEach打印结果**/public static void fibStreamB( ) {LongStream fibLongStream = fibStream().map(fib -> fib[0]).mapToLong(k->k).limit(30); //前30项fibLongStream.forEach(System.out::println);}public static void main(String[] args) {fibStreamA();fibStreamB();}
}相关文章:

java编程 斐波拉契数列算法集锦【斐波拉契数列】【下】【集合类】【Stream函数式编程】
斐波那契数列(Fibonacci sequence),又称黄金分割数列,是一个非常经典的递归问题。斐波那契数列的算法描述: 斐波那契数列,一个令人着迷而又充满神秘色彩的数字序列,它以0和1作为起始ÿ…...

智慧园区三维可视化平台
背景 随着物联网、人工智能等新一代信息技术的发展,数字孪生技术逐渐成为实现这一目标的关键工具。数字孪生技术能够对物理世界进行高精度、全要素的映射,并实时动态反映其变化情况,从而为园区提供精准的管理和服务。 方案简介 智慧园区数字…...

Redis 有序集合【实现排行榜】
使用 Redis 的 Sorted Set 数据结构可以非常高效地实现实时排行榜功能。Sorted Set 允许将元素按分数进行排序,同时支持插入、删除和查询操作,且这些操作的时间复杂度较低,非常适合处理高并发的场景。 实现思路 插入操作:当用户…...

ORACLE数据库管理系统介绍
1.ORACLE的特点: 可移植性 ORACLE采用C语言开发而成,故产品与硬件和操作系统具有很强的独立性。从大型机到微机上都可运行ORACLE的产品。可在UNIX、DOS、Windows等操作系统上运行。可兼容性 由于采用了国际标准的数据查询语言SQL,与IBM的SQL/DS、DB2等均兼容。并提供读取其它…...

C# 中Linq探讨 Or条件拼接
在C#中,没有直接内置于.NET Core或.NET Framework中的NuGet包能够直接“拼接”LINQ的OR条件,因为LINQ本身设计为一种声明式编程模型,用于查询数据集合。然而,你可以通过一些方式来实现多个条件以OR逻辑组合的效果,而不…...

有关应用层面试题有关库的思维导体
面试题目: TCP通信中3次握手和四次挥手? 答: 第一次握手:客户端发送SYN包(SYN1, seq0)给服务器,并进入SYN_SENT状态,等待服务器返回确认包。第二次握手:服务器接收到S…...

记一次 SAP BP 编号范围错误引发的一个问题 GET_NRIV_LINE
本来想着循着错误提示去排查,但是还是想看看业务发生了什么,他们的操作是否有问题,不经意间发现 号码段是有问题的,由此大概可以判断是他们编号范围和类型之间的问题 角色和分组是否一致的,如果不一致就发生了以上错误…...

(17)ELK大型储存库的搭建
前言: els是大型数据储存体系,类似于一种分片式存储方式。elasticsearch有强大的查询功能,基于java开发的工具,结合logstash收集工具,收集数据。kibana图形化展示数据,可以很好在大量的消息中准确的找到符…...
)
每日一问:Kafka消息丢失与堆积问题分析(简化版)
Kafka 消息系统问题解析 在本篇博客中,我们将深入探讨 Kafka 中常见的两大问题:消息丢失和消息堆积。首先,我们将简要介绍 Kafka 的基本工作原理,随后分别分析消息丢失和堆积的原因,并提供针对性的解决方案。 关于其详…...

C语言中函数sizeof和strlen区别
sizeof和strlen是C语言中的两个常用函数,它们的作用和使用方式有所不同。 sizeof sizeof是一个运算符而非函数,用于计算数据类型或变量占用的字节数。它可以计算任意数据类型(包括基本类型、自定义结构体、数组等)的大小。例如&…...
---- Python + MinIO + Kafka进阶)
RAG与LLM原理及实践(14)---- Python + MinIO + Kafka进阶
目录 背景 根因分析 配置 构造 创建 network 构造 zookeeper 构造 kafka 参数构造 原理解析 图解 全过程解析 工具使用 kafkacat 查看 broker python 实现 python send + kafka recv python 代码 kafka recv 运行效果 python recv + kafka send python 代…...

接口自动化-代码实现
接口自动化基础 1、接口自动化测试 接口自动化:使用工具或代码代替人对接口进行测试的技术测试目的: 防止开发修改代码时引入新的问题测试时机: 开发进行系统测试转测前,可以先进行接口自动化脚本的编写开发进行系统测试转测后&…...

如何查看linux大文件
文章目录 一、查看存储情况二、查看指定路径下的文件大小查看临时文件和日志的大小 三、查找home目录下文件大小大于100M的大文件四、查看INNODE使用情况五、查看进程使用情况查看所有进程查看特定进程杀死相关进程 六、清除缓存操作七、 查看docker的硬盘占用情况详细查看 一、…...

生成式人工智能服务大模型备案答疑
问:大模型备案范围 答:利用生成式人工智能技术向中华人民共和国境内公众提供生成文本、图片、音频、视频等内容的服务,适用本办法。 未向境内公众提供生成式人工智能服务的,不适用本办法的规定。 ps:生成式人工智能…...
QT-贪吃蛇小游戏
QT-贪吃蛇小游戏 一、演示效果二、核心代码三、下载链接 一、演示效果 二、核心代码 #include "Food.h" #include <QTime> #include <time.h> #include "Snake.h"Food::Food(int foodSize):foodSize(foodSize) {coordinate.x -1;coordinate.…...

虚幻5|AI视力系统,听力系统,预测系统(1)视力系统
继宠物伴随系统初步篇后续 虚幻5|AI巡逻宠物伴随及定点巡逻—初步篇-CSDN博客 一,听力系统 1.打开宠物ai的角色蓝图 2.选中ai感知组件 右侧细节,找到ai感知,添加感知配置,我们需要的是ai视力配置 3.选中左侧创建的ai感知组件&…...

IC rankIC
IC IC衡量的是预测值和实际值之间的相关系数 计算公式为:IC Pearson(R(predicted),R(actual)) 取值范围:[-1, 1],其中1表示完全相关,也就是预测值和实际值完全一样。0表示完全不相关,-1表示,反向相关 ra…...

Windows服务器IIS7下如何查看真实报错原因
背景 IIS7默认为友好报错,或只报错代码。如500错误,401错误等。根据这些错误无法定位真实原因,故而需要显示真实的错误信息。 解决方案 以500错误为例说明。 1、打开IIS,点全局设置中的"错误页"(注意必须是全局网站)。 2、右击50…...

深度学习设计模式之策略模式
文章目录 前言一、介绍二、特点三、详细介绍1.核心组成2.代码示例3.优缺点优点缺点 4.使用场景 总结 前言 策略模式定义一系列算法,封装每个算法,并使它们可以互换。 一、介绍 策略模式(Strategy Pattern)是一种行为型设计模式&…...
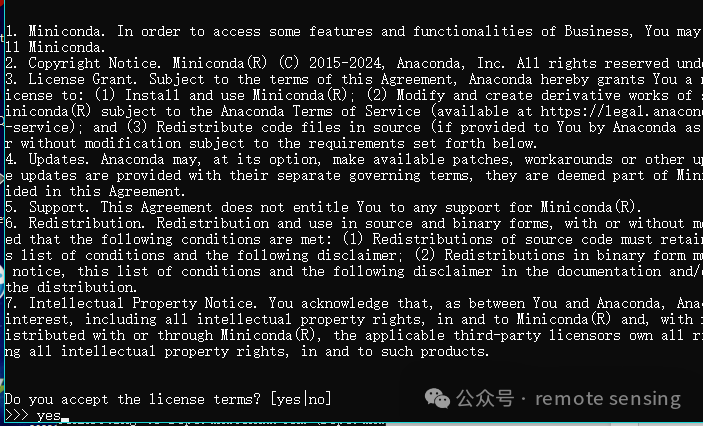
Linux 下安装miniconda(少走弯路)
Miniconda 和 Conda 都是用于管理 Python(及其他语言)环境和包的工具。 conda对于我来说是太臃肿了,很多的包我不会使用,所以选择安装miniconda是一个较好的选择。 下面是linux安装miniconda的实际操作。 在以下的网站…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
