数据结构——顺序栈和链式栈
目录
引言
栈的定义
栈的分类
栈的功能
栈的声明
1.顺序栈
2.链式栈
栈的功能实现
1.栈的初始化
(1)顺序栈
(2)链式栈
(3)复杂度分析
2.判断栈是否为空
(1)顺序栈
(2)链式栈
(3)复杂度分析
3.返回栈顶元素
(1)顺序栈
(2)链式栈
(3)复杂度分析
4.返回栈的大小
(1)顺序栈
(2)链式栈
(3)复杂度分析
5.元素入栈
(1)顺序栈
(2)链式栈
(3)复杂度分析
6.元素出栈
(1)顺序栈
(2)链式栈
(3)复杂度分析
7.打印栈的元素
(1)顺序栈
(2)链式栈
(3)复杂度分析
8.销毁栈
(1)顺序栈
(2)链式栈
(3)复杂度分析
顺序栈和链式栈的对比
完整代码
1.顺序表
2.链式表
结束语
引言
在学习完链表之后,我们接下来学习数据结构——栈的内容。
栈的定义
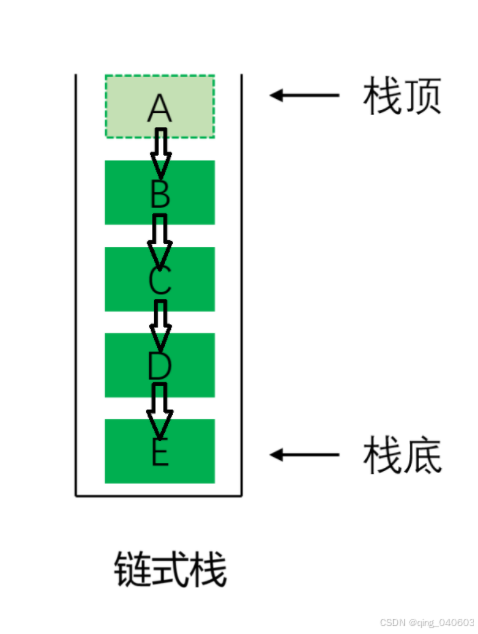
栈(Stack)是一种遵循后进先出(LIFO, Last In First Out)原则的有序集合。这种数据结构只允许在栈顶进行添加(push)或删除(pop)元素的操作。换句话说,最后添加到栈中的元素将是第一个被移除的,就像一叠盘子那样,我们只能从上面开始取放盘子。
如图所示:

栈顶(Top):栈顶是栈中最后添加(push)元素的位置,也是最先被移除(pop)或查看(peek/top)的元素所在的位置。在栈的所有操作中,无论是添加、删除还是查看元素,都是针对栈顶进行的。因此,栈顶是栈中最活跃、最频繁被访问的位置。
栈底(Bottom):栈底是栈中最早被添加进去的元素所在的位置,也是栈中唯一一个固定不变的位置(除非整个栈被清空)。在栈的常规操作中,栈底元素不会被直接访问,除非是将整个栈的内容倒序输出或者栈被完全清空。因此,栈底在栈的操作中扮演的是一个相对静态的角色。
栈的分类
栈可以分为顺序栈与链式栈。
如下图所示:
顺序栈:

链式栈:
栈的功能
我们要实现的栈的功能如下所示:
1.栈的初始化。
2.判断栈是否为空。
3.返回队头元素。
4.返回栈的大小。
5.元素入栈。6.元素出栈。
7.打印栈的元素。
8.销毁栈。
栈的声明
1.顺序栈
顺序栈的声明需要一个指向一块空间的指针a,指向栈顶下一个元素的top,以及标志栈空间大小的capacity。
声明如下:
typedef int STDataType;typedef struct STDataType
{STDataType* a;int top;int capacity;
}ST;2.链式栈
链式栈的声明只需要一个top指针,以及栈的容量capacity。
当然这里需要链表的声明。
代码如下:
typedef int STDataType;typedef struct SListNode
{STDataType data;struct SListNode* next;
}SLTNode;typedef struct Stack
{// 指向栈顶节点的指针SLTNode* top;int size;
}ST;栈的功能实现
1.栈的初始化
顺序栈和链式栈都可以先初始为NULL。
(1)顺序栈
顺序栈可以将top设置为-1,capacity设置为0。
代码如下:
//栈的初始化
void STInit(ST* st)
{assert(st);st->a = NULL;st->top = -1;st->capacity = 0;
}
(2)链式栈
链式栈将size设置为0,top设置为NULL。
代码如下:
//栈的初始化
void STInit(ST* st)
{assert(st);st->size = 0;st->top = NULL;
}
(3)复杂度分析
时间复杂度:由于顺序栈和链式栈花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
2.判断栈是否为空
判断栈是否为空只需要判断top的指向。
(1)顺序栈
当top=-1则为空。
代码如下:
//判空
bool STEmpty(ST* st)
{assert(st);return st->top == -1;
}
(2)链式栈
判断top是否指向NULL。
代码如下:
//判空
bool STEmpty(ST* st)
{return (st->top == NULL);
}(3)复杂度分析
时间复杂度:由于顺序栈和链式栈花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
3.返回栈顶元素
(1)顺序栈
//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);// 断言确保栈不为空(即栈顶索引不小于0)assert(st->top >= 0);return st->a[st->top];
}(2)链式栈
//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);assert(!STEmpty(st));return st->top->data;
}(3)复杂度分析
时间复杂度:由于顺序栈和链式栈花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
4.返回栈的大小
(1)顺序栈
由于在一开始将top设置为-1,需要top+1才能符合需要。
代码如下:
//获取数据个数
STDataType STSize(ST* st)
{assert(st);return st->top + 1;
}(2)链式栈
//获取数据个数
STDataType STSize(ST* st)
{return st->size;
}(3)复杂度分析
时间复杂度:由于顺序栈和链式栈花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
5.元素入栈
注意:入栈需要检查空间是否足够。
(1)顺序栈
由于top设置的是-1,因此需要先腾出空间然后再将新元素x放在栈顶。
代码如下:
//入栈
void STPush(ST* st, STDataType x)
{assert(st);// 注意:由于top初始化为-1,所以满的条件是top == capacity - 1if (st->top == st->capacity - 1){// 如果栈已满,则扩展栈的容量int newcapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->a, newcapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail:");return;}st->a = tmp;st->capacity = newcapacity;}// 增加栈顶索引,为新元素腾出空间st->top++;// 将新元素x存储在栈顶位置st->a[st->top] = x;
}(2)链式栈
//入栈
void STPush(ST* st, STDataType x)
{SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));if (newnode == NULL){perror("malloc fail:");return;}// 新节点的next指向原来的栈顶newnode->next = st->top;// 设置新节点的数据newnode->data = x;// 更新栈顶为新节点st->top = newnode;st->size++;
}(3)复杂度分析
时间复杂度:由于顺序栈支持下标的随机访问并且我们以单链表的头作为栈顶,因此时间复杂度为O(1)。
空间复杂度:顺序表又可能需要进行扩容处理,最坏的情况是空间复杂度为O(n)。链式表每次入栈固定为一个节点,因此空间复杂度为O(1)。
6.元素出栈
(1)顺序栈
//出栈
void STPop(ST* st)
{assert(st);assert(st->top >= 0);st->top--;
}(2)链式栈
//出栈
void STPop(ST* st)
{assert(st);assert(!STEmpty(st));// 获取栈顶节点的下一个节点SLTNode* next = st->top->next;free(st->top);// 更新栈顶指针,使其指向新的栈顶节点st->top = next;st->size--;
}(3)复杂度分析
时间复杂度:由于顺序栈还是链式栈花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
7.打印栈的元素
(1)顺序栈
//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));// 从栈顶开始打印,直到栈底(但不包括索引-1)for (int i = st->top; i >= 0; i--){printf("%d ", st->a[i]);}
}(2)链式栈
//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));for (SLTNode* top = st->top; top != NULL; top = top->next){printf("%d ", top->data);}
}(3)复杂度分析
时间复杂度:由于顺序栈和链式栈打印都需要遍历整个栈,因此时间复杂度为O(N)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
8.销毁栈
(1)顺序栈
//栈的销毁
void STDestory(ST* st)
{assert(st);free(st->a);st->a = NULL;st->capacity = 0;st->top = -1;
}
(2)链式栈
//栈的销毁
void STDestory(ST* st)
{assert(st);SLTNode* top = st->top;while (top != NULL){SLTNode* next = top->next;free(top);top = next;}st->size = 0;
}(3)复杂度分析
时间复杂度:由于顺序栈还是链式栈花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于顺序栈和链式栈花费空间都是一个固定大小的空间,因此空间复杂度为O(1)。
顺序栈和链式栈的对比
| 顺序栈 | 链式栈 | |
| 数据结构 | 使用动态数组实现,元素在物理内存中连续存储 | 使用链表实现,元素通过节点和指针连接,内存空间不连续 |
| 内存管理 | 栈空间不足时可动态扩容,释放整个栈时一次性释放内存 | 节点内存单独分配和释放,需要遍历链表以释放所有节点内存 |
| 时间效率 | 可以通过数组下标直接访问栈内任意位置的元素,但是这不符合栈的定义 | 由于每次都需要扩容操作,所以效率略比顺序栈低 |
| 空间效率 | 顺序栈的扩容较大可能会造成空间的浪费 | 内存使用相对灵活,但每个节点需要额外存储指针 |
完整代码
1.顺序表
Stack.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;typedef struct STDataType
{STDataType* a;int top;int capacity;
}ST;//栈的初始化
void STInit(ST* st);//栈的销毁
void STDestory(ST* st);//入栈
void STPush(ST* st, STDataType x);
//出栈
void STPop(ST* st);//取出栈顶数据
STDataType STTop(ST* st);//判空
bool STEmpty(ST* st);//获取数据个数
STDataType STSize(ST* st);//栈的打印
void STPrint(ST* st);Stack.c
#include"Stack.h"//栈的初始化
void STInit(ST* st)
{assert(st);st->a = NULL;st->top = -1;st->capacity = 0;
}//栈的销毁
void STDestory(ST* st)
{assert(st);free(st->a);st->a = NULL;st->capacity = 0;st->top = -1;
}//入栈
void STPush(ST* st, STDataType x)
{assert(st);// 注意:由于top初始化为-1,所以满的条件是top == capacity - 1if (st->top == st->capacity - 1){// 如果栈已满,则扩展栈的容量int newcapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->a, newcapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail");return;}st->a = tmp;st->capacity = newcapacity;}// 增加栈顶索引,为新元素腾出空间st->top++;// 将新元素x存储在栈顶位置st->a[st->top] = x;
}//出栈
void STPop(ST* st)
{assert(st);assert(st->top >= 0);st->top--;
}//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);assert(st->top >= 0);return st->a[st->top];
}//判空
bool STEmpty(ST* st)
{assert(st);return st->top == -1;
}//获取数据个数
STDataType STSize(ST* st)
{assert(st);return st->top + 1;
}//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));// 从栈顶开始打印,直到栈底(但不包括索引-1)for (int i = st->top; i >= 0; i--){printf("%d ", st->a[i]);}
}2.链式表
Stack.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;typedef struct SListNode
{STDataType data;struct SListNode* next;
}SLTNode;typedef struct Stack
{// 指向栈顶节点的指针SLTNode* top;int size;
}ST;//栈的初始化
void STInit(ST* st);//栈的销毁
void STDestory(ST* st);//入栈
void STPush(ST* st, STDataType x);//出栈
void STPop(ST* st);//取出栈顶数据
STDataType STTop(ST* st);//判空
bool STEmpty(ST* st);//获取数据个数
STDataType STSize(ST* st);//栈的打印
void STPrint(ST* st);Stack.c
#include"Stack.h"//栈的初始化
void STInit(ST* st)
{assert(st);st->size = 0;st->top = NULL;
}//栈的销毁
void STDestory(ST* st)
{assert(st);SLTNode* top = st->top;while (top != NULL){SLTNode* next = top->next;free(top);top = next;}st->size = 0;
}//入栈
void STPush(ST* st, STDataType x)
{SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));if (newnode == NULL){perror("malloc fail:");return;}// 新节点的next指向原来的栈顶newnode->next = st->top;// 设置新节点的数据newnode->data = x;// 更新栈顶为新节点st->top = newnode;st->size++;
}//出栈
void STPop(ST* st)
{assert(st);assert(!STEmpty(st));// 获取栈顶节点的下一个节点SLTNode* next = st->top->next;free(st->top);// 更新栈顶指针,使其指向新的栈顶节点st->top = next;st->size--;
}//取出栈顶数据
STDataType STTop(ST* st)
{assert(st);assert(!STEmpty(st));return st->top->data;
}//判空
bool STEmpty(ST* st)
{return (st->top == NULL);
}//获取数据个数
STDataType STSize(ST* st)
{return st->size;
}//栈的打印
void STPrint(ST* st)
{assert(st);assert(!STEmpty(st));for (SLTNode* top = st->top; top != NULL; top = top->next){printf("%d ", top->data);}
}结束语
本篇博客简要介绍了一下栈,接下来我们将接着学习与栈有些类似的另一个数据结构——队列。
数据结构——链式队列和循环队列
感谢各位大佬们的支持!!!
求点赞收藏关注!!!
十分感谢!!!
相关文章:

数据结构——顺序栈和链式栈
目录 引言 栈的定义 栈的分类 栈的功能 栈的声明 1.顺序栈 2.链式栈 栈的功能实现 1.栈的初始化 (1)顺序栈 (2)链式栈 (3)复杂度分析 2.判断栈是否为空 (1)顺序栈 (2)链式栈 (3)复杂度分析 3.返回栈顶元素 (1)顺序栈 (2)链式栈 (3)复杂度分析 4.返回栈的大…...

PHP轻创推客集淘客地推任务平台于一体的综合营销平台系统源码
🚀轻创推客,营销新纪元 —— 集淘客与地推任务于一体的全能平台🌐 🌈【开篇:营销新潮流,轻创推客引领未来】 在瞬息万变的营销世界里,你还在为寻找高效、全面的营销渠道而烦恼吗?&…...

three.js实现 加载3dtiles ,瓦片 ,倾斜摄影,功能
预览:https://z2586300277.github.io/three-cesium-examples/#/codeMirror?navigationThreeJS&classifyexpand&idloadTiles 部署站点预览:http://threehub.cn/ 开源地址:https://z2586300277.github.io/three-cesium-examples/#/e…...

Qt QTextEdit调用append数据重复的问题
使用QTextEdit写了个串口工具, 当串口有数据时通过一个signal传给slot,在 slot中调用QTextEdit的append(text)来增量显示串口数据,当串口关闭时调用clear()来清空显示。 结果发现append调用后显示的数据会有重复。 分析 分析代码࿰…...

数学基础(二)
一、导数 导数计算: 偏导数: 方向导数: 梯度: 函数在某点的梯度是一个向量,它的方向余方向导数最大值取得的方向一致。其大小正好是最大的方向导数 二、微积分 面积由来: 切线: 定积分&#x…...

Java设计模式原则及中介者模式研究
在软件开发过程中,设计模式作为解决常见设计问题的有效工具,对于提升代码质量、促进团队协作具有重要意义。本文系统地阐述了Java设计模式的六大基本原则——单一职责原则、开放封闭原则、里氏替换原则、依赖倒置原则、接口隔离原则以及迪米特法则&#…...

logstash入门学习
1、入门示例 1.1、安装 Redhat 平台 rpm --import http://packages.elasticsearch.org/GPG-KEY-elasticsearch cat > /etc/yum.repos.d/logstash.repo <<EOF [logstash-5.0] namelogstash repository for 5.0.x packages baseurlhttp://packages.elasticsearch.org…...

【代码】Swan-Transformer 代码详解(待完成)
1. 局部注意力 Window Attention (W-MSA Module) class WindowAttention(nn.Module):r""" Window based multi-head self attention (W-MSA) module with relative position bias.It supports both of shifted and non-shifted window.Args:dim (int): Number…...

iframe.contentDocument 和document.documentElement的区别
iframe.contentDocument 和 document.documentElement 是用于访问不同内容的两个不同的对象或属性。 1. iframe.contentDocument 内容: iframe.contentDocument 代表的是 <iframe> 元素所嵌入的文档的 Document 对象。它允许你访问和操作嵌入的文档(即 ifram…...
)
计算机操作员试题(中篇)
计算机操作员试题(中篇) 335.在 Excel中,把鼠标指向被选中单元格边框,当指变成箭头时,拖动鼠标到目标单 元格时,将完成( )操作。 (A)删除 (B)移动 ©自动填充 (D)复制 336.在 Excel 工作表的单元格中,如想输入数字字符串 070615 (例如学号),则应输 入()。 (A) 0007…...
车规级MCU「换道」竞赛
汽车芯片,尤其是MCU市场正在进入拐点期。 本周,总部位于荷兰的汽车芯片制造商—恩智浦(NXP)半导体总裁兼首席执行官Kurt Sievers在公司第二季度财报电话会议上告诉投资者,由于汽车需求停滞不前,该公司正在努…...

数学生物学-2-离散时间模型(Discrete Time Models)
上一篇介绍了一个指数增长模型。然而,我们也看到,在现实情况下,细菌培养的增长是在离散的时间(在这种情况下是小时)进行测量的,种群并没有无限增长,而是趋于以S形曲线趋于平稳,称为“…...
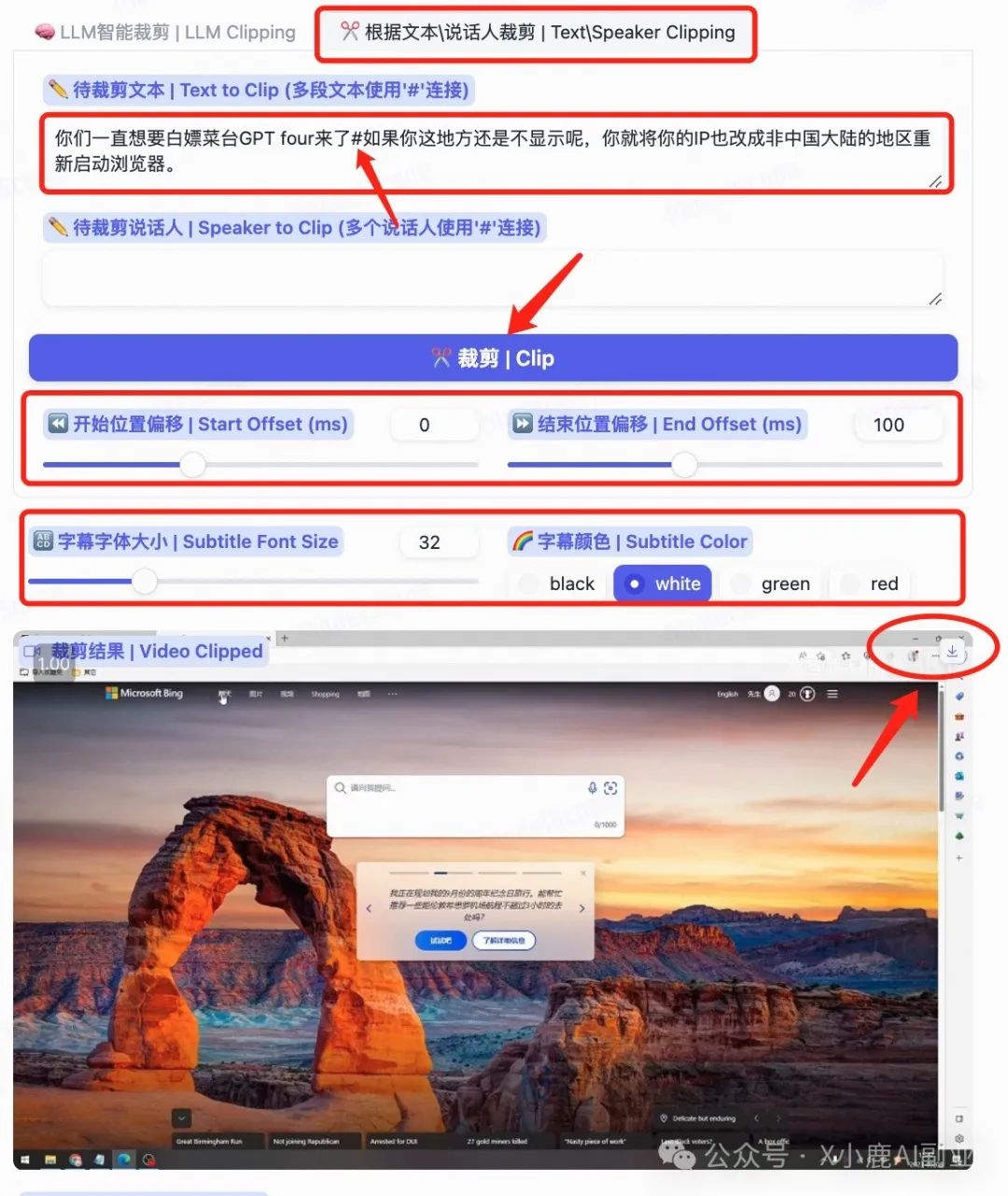
免费开源!AI视频自动剪辑已成现实!效率提升80%,打工人福音!(附详细教程)
大家好,我是程序员X小鹿,前互联网大厂程序员,自由职业2年,也一名 AIGC 爱好者,持续分享更多前沿的「AI 工具」和「AI副业玩法」,欢迎一起交流~ 想象一下,假设老板给你布置了一项任务:…...

NtripShare全站仪自动化监测之气象改正
最近有幸和自动化监测领域权威专家进行交流,讨论到全站仪气象改正的问题,因为有些观点与专家不太一致,所以再次温习了一下全站仪气象改正的技术细节。 气象改正的概念 全站仪一般利用光波进行测距,首先仪器会处理测距光波的相位漂…...

【人工智能】项目案例分析:使用自动编码器进行信用卡欺诈检测
一、项目背景 信用卡欺诈是金融行业面临的一个重要问题,快速且准确的欺诈检测对于保护消费者和金融机构的利益至关重要。本项目旨在通过利用自动编码器(Autoencoder)这一无监督学习算法,来检测信用卡交易中的欺诈行为,…...

【工控】线扫相机小结
背景简介 我目前接触到的线扫相机有两种形式: 无采集卡,数据通过网线传输。 配备采集卡,使用PCIe接口。 第一种形式的数据通过网线传输,速度较慢,因此扫描和生成图像的速度都较慢,参数设置主要集中在相机本身。第二种形式的相机配备采集卡,通常速度更快,但由于相机和…...

将Web应用部署到Tomcat根目录的三种方法
将应用部署到Tomcat根目录的三种方法 将应用部署到Tomcat根目录的目的是可以通过"http://[ip]:[port]"直接访问应用,而不是使用"http://[ip]:[port]/[appName]"上下文路径进行访问。 方法一:(最简单直接的方法࿰…...

工业和信息化部教育与考试中心计算机相关专业介绍
国家工信部的认证证书在行业内享有较高声誉。 此外,还设有专门的工业和信息化技术技能人才数据库查询服务,进一步方便了个人和企业对相关职业能力证书的查询需求。 序号 专业工种 级别 备注 1 JAVA程序员 初级 职业技术 2 电子…...

第二证券:生物天然气线上交易达成 创新探索互联互通、气证合一
8月20日,上海石油天然气生意中心在国内立异推出生物天然气线上生意。当日,绿气新动力(北京)有限公司(简称“绿气新动力”)挂单的1500万立方米生物天然气被百事食物(我国)有限公司&am…...

重磅!RISC-V+OpenHarmony平板电脑发布
仟江水商业电讯(8月18日 北京 委托发布)RISC-V作为历史上全球发展速度最快、创新最为活跃的开放指令架构,正在不断拓展高性能计算领域的边界。OpenHarmony是由开放原子开源基金会孵化并运营的开源项目,已成为发展速度最快的智能终…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
