了解 K-Means 聚类的工作原理（详细指南）

一、说明

        K-means 的目标是将一组观测值划分为 k 个聚类，每个观测值分配给均值（聚类中心或质心）最接近的聚类，从而充当该聚类的代表。

        在本文中，我们将全面介绍 k 均值聚类（最常用的聚类方法之一）及其组成部分的所有内容。我们将了解聚类，为什么它很重要，以及它的应用。

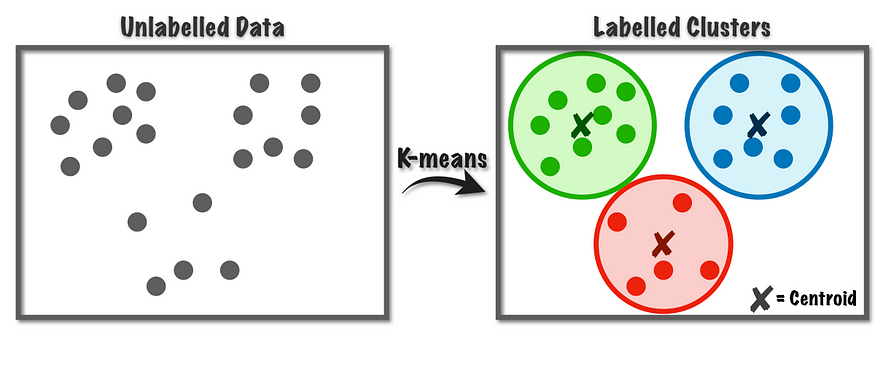
二、什么是 K-means 聚类？

        K-Means 聚类是一种流行的无监督机器学习算法，用于将数据集划分为一组不同的、不重叠的组或聚类。目标是以这样一种方式对数据点进行分组，即同一聚类中的点彼此之间比与其他聚类中的点更相似。该技术广泛应用于数据挖掘、市场细分、图像压缩以及其他需要模式识别的领域。

2.1 K-means 中使用的数学概念

        在我们开始计算 k 均值之前，我们将讨论 K 均值中使用的数学概念。

• 质心：这些是聚类的中心点，在每次迭代中都会重新计算，以作为分配给聚类的点的平均值。
• 欧几里得距离：这是 K-Means 中最常用的距离度量。它计算欧几里得空间中两点之间的直线距离。

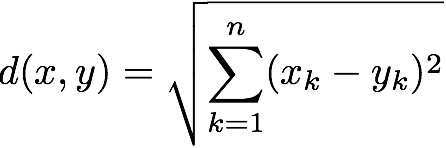
对于 n 维的 X（x1，x2,...,xn） 和 Y（y1，y2,...,yn） 2 个点，使用此公式测量欧几里得距离。

• 惯性：它衡量集群的分布程度。它是每个数据点与其分配的质心之间的平方距离之和。目标是将惯性降至最低。

WCSS = d1² + d2²+ d3² + ...........+ dn²

2.2 K-means是如何工作的？

# Generating Data
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs# Parameters
n_samples = 300
n_features = 2
centers = 4# Generate data
X, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=centers, cluster_std=3, random_state=42)# Visualize the data
plt.scatter(X[:, 0], X[:, 1], s=50, cmap='viridis')
plt.title("Initial Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

from sklearn.cluster import KMeanskmeans = KMeans(n_init = 10, n_clusters = 4, verbose=100)
kmeans.fit(X)y_kmeans = kmeans.predict(X)plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c = 'red', label = 'Cluster1')
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c = 'blue', label = 'Cluster2')
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c = 'green', label = 'Cluster3')
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c = 'yellow', label = 'Cluster4')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c = 'black', label = 'Centroids')plt.legend()plt.show()

1. 初始化：

• 选择簇数 K。
• 随机初始化 K 个质心，它们是数据集中表示每个聚类中心的点。

2. 分配步骤：

• 根据欧几里得距离将每个数据点分配给最近的质心。这将创建 K 个聚类。

我们计算一个点到每个质心的欧几里得距离，并将其放入距离最小的聚类中。

3. 更新步骤：

• 通过取分配给每个聚类的所有数据点的平均值来计算新的质心。

我们计算聚类中所有点的平均值，以获得新的质心。

4.重复：

• 使用新的质心重复分配和更新步骤，直到质心不再更改或更改低于预定义的阈值。

生成上述图像的代码在此处。

三、如何确定质心的数量？

3.1 弯头法

肘部方法是一种用于确定 K-Means 聚类中最佳聚类数的技术。这个想法是对 K 的值范围运行 K-Means，并计算从每个点到其分配的质心的距离平方和（称为惯性或簇内平方和）。随着 K 的增加，惯性减小，因为点更接近它们的质心。

目标是找到“肘点”，其中下降速度急剧减慢，表明随着 K 的增加，回报递减，即在肘点之后增加 K 的值没有多大好处。

WCSS = d1² + d2² + d3² + ...........+ dn²

我们通常计算前 10 个聚类的惯性。对于 K = 数据点数，惯性将为零。

from sklearn.cluster import KMeanswcss = []
for i in range(1, 11):kmeans = KMeans(n_init = 10, n_clusters = i)kmeans.fit(X)wcss.append(kmeans.inertia_)plt.title("Elbow Method")
plt.xlabel("Number of Clusters(k)")
plt.ylabel("WCSS")
plt.plot(range(1,11),wcss)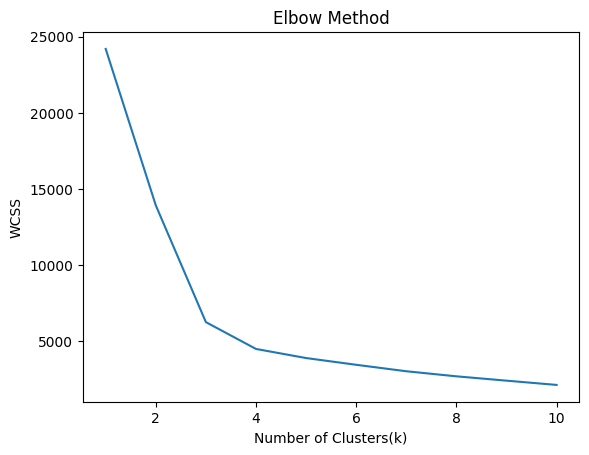

因此，集群的数量可以是 3 个或 4 个。

肘部方法有一些限制，例如：

1. 肘点的选择是主观的。
2. 它不适用于所有数据集，例如当聚类具有不规则形状或大量特征时。

3.2 剪影分数

Silhouette 分数是一个指标，用于量化集群的质量。它适用于任何聚类算法。

剪影分数的值从 -1 到 +1 不等。

• +1 ： 良好（集群分离良好）
• 0 ： 集群彼此靠近
• -1 ： 错误（错误的聚类）

内聚力： 同一聚类中元素彼此接近的程度。（它衡量集群的紧凑性。

分离： 它指的是不同的集群彼此之间有多么不同或分辨得多么好。

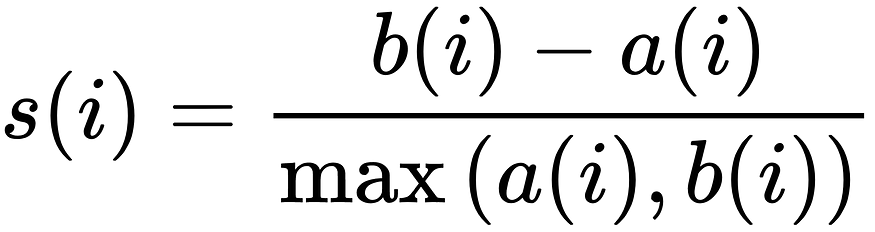
S（i） 是剪影分数。

a（i） 是所取点与其自身聚类中所有点的平均距离。它代表着凝聚力。

b（i） 是所取点与剩余最近聚类的所有点之间的平均聚类距离。它代表分离。

from sklearn.metrics import silhouette_score
sil = []
for i in range(2, 11):kmeans = KMeans(n_clusters=i)cluster_labels = kmeans.fit_predict(X)silhouette_avg = silhouette_score(X, cluster_labels)sil.append(silhouette_avg)plt.xlabel("Number of Clusters(k)")
plt.ylabel("Silhouette Score")
plt.plot(range(2,11),sil)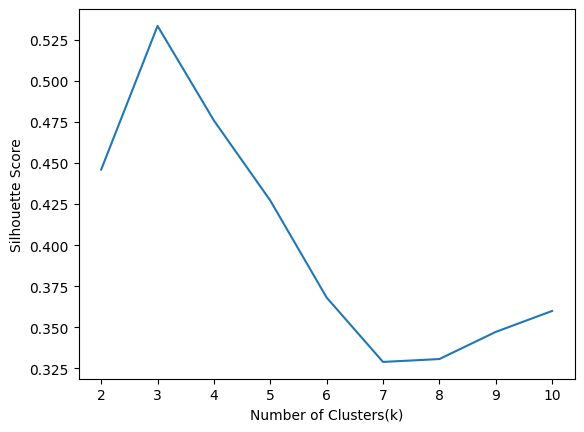

根据轮廓分数，我们应该假设 k=3，因为对于 3 个聚类，分数是最大的。

四、如何初始化质心？

4.1 K-均值++

K-Means++ 是 K-Means 聚类算法的高级版本，它改进了质心的初始选择，旨在提高聚类结果和收敛速度。标准的 K-Means 算法对质心的初始放置很敏感，初始化不良会导致聚类次优和收敛速度变慢。K-Means++ 通过使用更智能的初始化策略来解决这个问题。

4.2 K-Means++ 初始化的步骤

1. 选择第一个质心：
• 从数据集中随机选择第一个质心。
2. 选择后续质心：
• 对于每个后续质心，计算从每个
数据点 x 到最近的已选质心的距离 D（x）。
• 从数据点中选择下一个质心，其概率与 D（x）² 成正比。概率最大的点作为质心。（我们采用概率而不是距离本身来减少异常值的影响。
3. 重复：
• 重复该过程，直到选择 K 个质心。
4. 继续使用标准 K-Means：
• 使用这些 K 质心作为初始起点，并运行标准 K-Means 算法

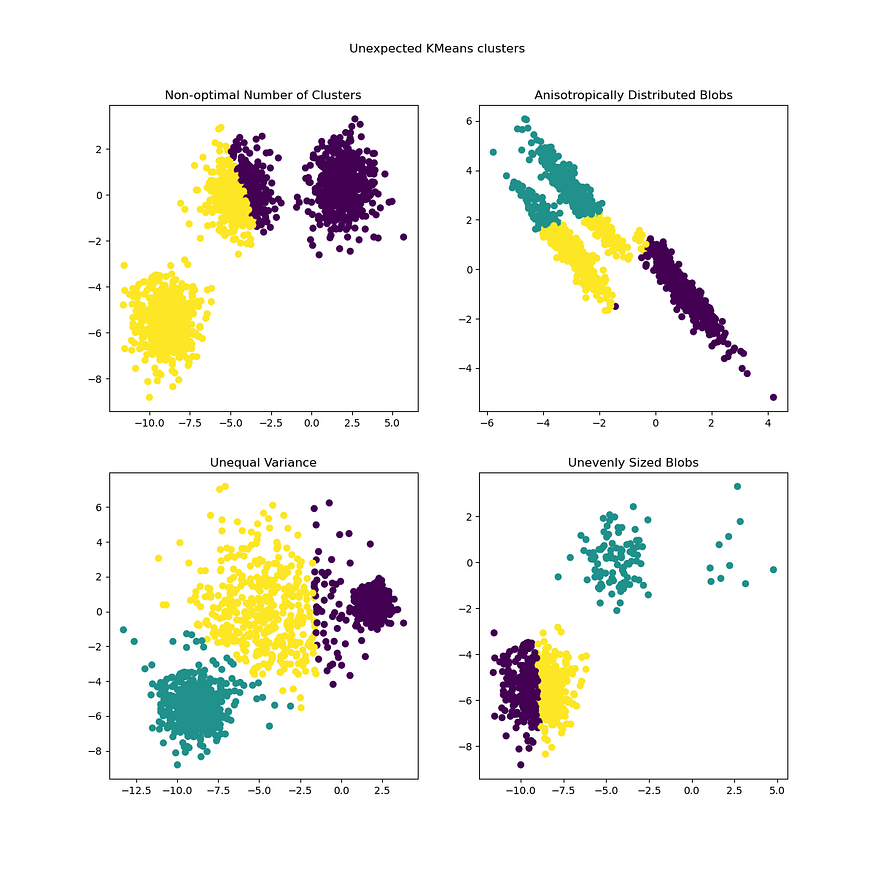
五、K-means的假设和局限性

1. 假设簇是球形和各向同性（不是不规则形状）。
2. 假定聚类具有相似的大小。
3. 假设所有聚类都具有相似的方差。
4. 集群的数量是预定义的。
5. 当聚类分离良好时，此算法效果最佳。
6. K 均值不能在存在异常值的情况下应用（因为质心会移动太多并且无法正确分配）

六、结论

K-Means 简单性和效率使其成为各种应用的热门选择，包括图像分割、市场分割和模式识别。尽管它很简单，但它为各个领域的许多应用程序提供了坚实的基础。但是，它对质心的初始放置很敏感，这可能导致次优聚类。尽管存在一些局限性，例如对 K 选择的敏感性以及卡在局部最小值中的可能性，但 K-Means 仍然是数据分析和机器学习中一种基本且高效的聚类技术。

K-Means 有其局限性，其他聚类算法（如 DBSCAN 和 GMM）可以克服这些局限性。

K 表示

聚类