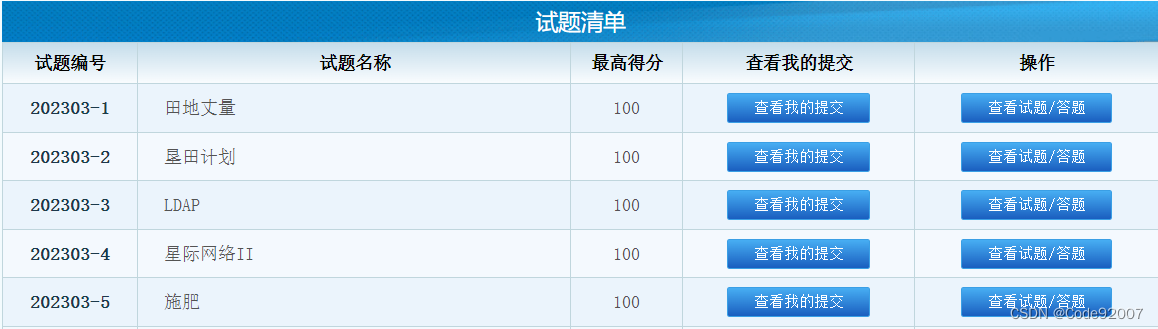
CCF-CSP认证 202303 500分题解
202303-1 田地丈量(矩阵面积交)
矩阵面积交=x轴线段交长度*y轴线段交长度
线段交长度,相交的时候是min右端点-max左端点,不相交的时候是0
#include<bits/stdc++.h>
using namespace std;
int n,a,b,ans,x,y,x2,y2;
int f(int l1,int r1,int l,int r){return max(0,min(r1,r)-max(l1,l));
}
int main(){cin>>n>>a>>b;for(int i=1;i<=n;++i){cin>>x>>y>>x2>>y2;ans+=f(0,a,x,x2)*f(0,b,y,y2);}cout<<ans<<endl;return 0;
}202303-2 垦田计划(二分)
二分最终答案x(x>=k),判断降到x天资源是否够
够的话就往小里二分,否则往大里二分,
当然贪心也可以做,排序之后,把最耗时的天数逐个压低,使得后缀和前面持平
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,m,k,t[N],c[N],mx;
bool ok(int x){ll sum=0;for(int i=1;i<=n;++i){if(t[i]<=x)continue;sum+=1ll*(t[i]-x)*c[i];if(sum>m)return 0;}return 1;
}
int main(){cin>>n>>m>>k;for(int i=1;i<=n;++i){cin>>t[i]>>c[i];mx=max(mx,t[i]);}int l=k,r=mx;while(l<=r){int mid=(l+r)/2;if(ok(mid))r=mid-1;else l=mid+1;}cout<<l<<endl;return 0;
}202303-3 LDAP(模拟+栈+bitset)
主要是要解决表达式嵌套的问题,
与栈实现计算器时维护一个符号栈、一个数值栈类似
这里维护了两个栈,一个符号栈op,一个bitset集合栈stk,集合求交、或,由bitset完成
当遇到&或|时,将符号压栈;当遇到)时,将bitset压栈;()内正常读取,求bitset即可
当同一个符号对应两个bitset在栈内(num[c]=2)时,将两个bitset运算为一个bitset
其余部分map乱搞,q[i][j]表示DN=i用户的j属性值,
p(i,j)表示i属性值为j的有哪些用户,has[i]表示i属性有哪些用户,
i:j操作时,p[i][j]即为所求;i~j操作时,has[i]内去掉p[i][j]即为所求
to[i]记录了第i个用户对应的DN值,输出时按DN从小到大排序即可
实际耗时3s多,12s绰绰有余
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
const int N=2502;
int n,m,sz,id,k,c,d,x,y,num[N],to[N],f[N];
map<int,int>q[N];
map<P,vector<int>>p;
map<int,vector<int>>has;
char s[N],op[N];
bitset<N>stk[N*2],res;
bitset<N>cal(int l,char x,int r){bitset<N>ans;for(auto &v:p[P(l,r)]){ans.set(v);}if(x=='~'){for(auto &v:has[l]){ans.flip(v);}}return ans;
}
int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d%d",&id,&k);to[i]=id;for(int j=1;j<=k;++j){scanf("%d%d",&x,&y);q[i][x]=y;has[x].push_back(i);p[P(x,y)].push_back(i);}}scanf("%d",&m);for(int i=1;i<=m;++i){scanf("%s",s);sz=strlen(s);c=d=0;for(int j=0;j<sz;){if(s[j]=='&' || s[j]=='|'){op[++c]=s[j++];}else if(s[j]=='('){j++;}else if(s[j]==')'){num[c]++;if(num[c]==2){d--;if(op[c]=='&')stk[d]=stk[d]&stk[d+1];else stk[d]=stk[d]|stk[d+1];num[c--]=0;}j++;}else{int cur=j,l=0,r=0;while(cur<sz && (s[cur]!=':' && s[cur]!='~')){l=l*10+(s[cur]-'0');cur++;}char x=s[cur++];while(cur<sz && s[cur]!=')'){r=r*10+(s[cur]-'0');cur++;}stk[++d]=cal(l,x,r);j=cur;}}int e=0;for(int j=1;j<=n;++j){if(stk[d].test(j)){f[++e]=to[j];}}sort(f+1,f+e+1);for(int j=1;j<=e;++j){printf("%d%c",f[j]," \n"[j==e]);}if(!e)puts("");}return 0;
}202303-4 星际网络II(线段树)
线段树(离散化、单点询问、区间求和、区间最值),经典题了
线段树维护区间和,用于记录对应区间几个值被用过
线段树维护最大最小值,用于记录被哪个用户id用过,
当最小值=最大值时,表示恰被一个用户用过
首先,将最大32维的数转10进制,压成长为32的array,
离散化去重后,找到每个ip地址对应下标映射
操作1:若[l,r]是否没被用户用过,或[l,r]仅被当前用户用过且没占满,则可行,否则不可行
线段树先查一下这段区间和,等于0表示没被用过,则可行
否则,判一下当前区间最大最小值,若最大最小值相等且区间和小于区间长度,则可行
操作2:单点询问,查单点最大/最小值即可知道被哪个用户用过,或没用过
操作3:区间询问,若[l,r]仅被一个用户全用过,则区间和为区间长度,区间最大最小值相等
注意离散化时,需要给右端点+1的值也离散化进去,并考虑+1带来的进位问题
否则,可能会出现[1,2][4,5]在离散化前不相邻,离散化后变为[1,2][3,4]相邻的情形
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=15e4+10,M=5e4+10,K=170,B=32,INF=0x3f3f3f3f;
struct segtree{int n;struct node{int l,r,v,c,mn,mx;}e[N<<2];#define l(p) e[p].l#define r(p) e[p].r#define v(p) e[p].v#define c(p) e[p].c#define mn(p) e[p].mn#define mx(p) e[p].mxvoid up(int p){v(p)=v(p<<1)+v(p<<1|1);mn(p)=min(mn(p<<1),mn(p<<1|1));mx(p)=max(mx(p<<1),mx(p<<1|1));}void bld(int p,int l,int r){l(p)=l;r(p)=r;c(p)=0;if(l==r){v(p)=0;mn(p)=INF;mx(p)=-INF;return;}int mid=l+r>>1;bld(p<<1,l,mid);bld(p<<1|1,mid+1,r);up(p);}void psd(int p){if(c(p)){v(p<<1)=r(p<<1)-l(p<<1)+1;mn(p<<1)=min(mn(p<<1),c(p));mx(p<<1)=max(mx(p<<1),c(p));c(p<<1)=c(p);v(p<<1|1)=r(p<<1|1)-l(p<<1|1)+1; mn(p<<1|1)=min(mn(p<<1|1),c(p));mx(p<<1|1)=max(mx(p<<1|1),c(p));c(p<<1|1)=c(p);c(p)=0; }}void init(int _n){n=_n;bld(1,1,n);}void chg(int p,int ql,int qr,int v){if(ql>qr)return;if(ql<=l(p)&&r(p)<=qr){v(p)=r(p)-l(p)+1;mn(p)=min(mn(p),v);mx(p)=max(mx(p),v);c(p)=v;return;}psd(p);int mid=l(p)+r(p)>>1;if(ql<=mid)chg(p<<1,ql,qr,v);if(qr>mid)chg(p<<1|1,ql,qr,v);up(p);}int cnt(int p,int ql,int qr){if(ql<=l(p)&&r(p)<=qr)return v(p);int mid=l(p)+r(p)>>1,res=0;psd(p);if(ql<=mid)res+=cnt(p<<1,ql,qr);if(qr>mid)res+=cnt(p<<1|1,ql,qr);return res;}int amn(int p,int ql,int qr){if(ql<=l(p)&&r(p)<=qr)return mn(p);int mid=l(p)+r(p)>>1,res=INF;psd(p);if(ql<=mid)res=min(res,amn(p<<1,ql,qr));if(qr>mid)res=min(res,amn(p<<1|1,ql,qr));return res;}int amx(int p,int ql,int qr){if(ql<=l(p)&&r(p)<=qr)return mx(p);int mid=l(p)+r(p)>>1,res=-INF;psd(p);if(ql<=mid)res=max(res,amx(p<<1,ql,qr));if(qr>mid)res=max(res,amx(p<<1|1,ql,qr));return res;}
}seg;
int n,m,q,op,c;
array<int,B>f[N];
auto cal(string s){int d=0;array<int,B>ans={0};for(auto &y:s){if(y==':'){d++;continue;}int &v=ans[d];if('a'<=y && y<='f')v=v*16+(y-'a')+10;else v=v*16+(y-'0');}return ans;
}
auto add_one(array<int,B>y){y[n/16-1]++;for(int i=B-1;i;--i){if(y[i]>=65536){y[i]-=65536;y[i-1]++;}}return y;
}
int g(array<int,B>v){int x=lower_bound(f,f+c,v)-f;return x+1;
}
struct ask{int op,x;string s,t;void rd(){cin>>op;if(op==1)cin>>x;cin>>s;f[c++]=cal(s);if(op==2)t=s;else{cin>>t;f[c++]=cal(t);f[c]=add_one(f[c-1]);c++;}}void sol(){int l=g(cal(s)),r=g(cal(t)),w=seg.cnt(1,l,r);int mn=seg.amn(1,l,r),mx=seg.amx(1,l,r);if(op==1){if(!w || (w<r-l+1 && mn==mx && mn==x)){seg.chg(1,l,r,x);cout<<"YES"<<endl;}else{cout<<"NO"<<endl;}}else if(op==2){cout<<(mn==INF?0:mn)<<endl;}else{cout<<(w==r-l+1 && mn==mx?mn:0)<<endl;}}
}e[M];
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>q;for(int i=1;i<=q;++i){e[i].rd();}sort(f,f+c);c=unique(f,f+c)-f;seg.init(c+5);for(int i=1;i<=q;++i){e[i].sol();}return 0;
}202303-5 施肥(分治+线段树+树状数组)
n,m<=3000乱搞一下就ok,数据范围再小的就不提了
虽然事后发现,n,m<=3000的暴力,我是用的O(nmlogn),而官解是O(n^2+nm)
特殊性质的分也比较好判断,这样75分就到手了,然后就不会了,就去嫖了官解
这个做法本质是对O(n^2+nm)的暴力套了个分治,
虽然出题人说,两个满分,分别是用李超树和分块过的,感觉很神秘
理解了好久,花若干时间写完代码之后,交上去wa成sb,
对拍拍出来问题之后,交上去又T了,把回收改成区间删除才过
复杂度O((n+m)logm)也就是一个log,但是貌似被我实现成了两个log,感谢出题人不杀之恩
开了四棵线段树,树状数组常数比较小,最后也过了,讲一下中间遇到的各个做法
60分题解(O(n^2+nm)暴力)
按右端点增序枚举,假设当前枚举到的右端点为R,此时只能选右端点<=R的线段
记a[i]为对于i来说,只能选右端点<=R的线段时,能覆盖i的最大的左端点
那么,固定右端点R时,若[L,R]是一组解,一定有对于任意L<=i<=R,L<=a[i]
换言之,为了覆盖[L,R]中间的值,采用的线段,其左端点不能比L更靠左
所以,就可以一边枚举右端点,一边将线段插入,
插入一条线段[i,R]时,涉及到一段区间a值的动态修改,本质是区间[i,R]的a值和i取max
若i<j<=R,a[j]<a[i],那么,为了覆盖区间[i,R],实际左端点也需至少取到a[j]的位置
所以,实际计算贡献的时候,需要考虑后缀对当前值的影响,
维护后缀最小值,可以搞个单调栈,也可以逐项维护
后缀的数组,实际是形如1 1 1 3 3 10 10 10 10的分段阶梯数组,
值即为左端点的值,贡献为左端点出现的种类数
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
typedef long long ll;
const int N=2e5+10;
int n,m,l,r,a[N],suf[N];
ll ans;
vector<int>f[N];
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;++i){scanf("%d%d",&l,&r);f[r].push_back(l);}for(int i=1;i<=n;++i){for(auto &v:f[i]){for(int j=v;j<=i;++j){a[j]=max(a[j],v);}}suf[i]=a[i];ans+=(suf[i]>0);for(int j=i-1;j>=1;--j){suf[j]=min(suf[j+1],a[j]);if(suf[j]!=suf[j+1] && suf[j])ans++;}}printf("%lld\n",ans);return 0;
}75分题解(特殊性质)
特殊性质:不存在区间的相互包含关系
就是一堆相交区间,如果把两两相交的区间合并成一个连通块,
则组成若干个连通块,且连通块内是偏序的,
一定可以选一段连续的区间,取到左区间的左端点和右区间的右端点
所以,连通块内有x个区间时,对答案的贡献是x*(x+1)/2
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
typedef long long ll;
const int N=2e5+10;
int n,m,c,mx;
vector<int>f[N],st[N];
set<int>cur;
map<P,bool>vis;
ll ans,now[N];
struct node{int l,r;
}e[N],x;
bool operator<(node a,node b){return a.r<b.r;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;++i){scanf("%d%d",&x.l,&x.r);//e[++c]=x;if(!vis[P(x.l,x.r)])e[++c]=x;vis[P(x.l,x.r)]=1;}m=c;sort(e+1,e+m+1);if(n>3000){for(int i=1;i<=m;){int j=i,mx=e[j].r;while(j+1<=m && e[j+1].l<=mx+1){j++;mx=max(mx,e[j].r);}int sz=j-i+1;ans+=1ll*sz*(sz+1)/2;i=j+1;}printf("%lld\n",ans);}else{for(int i=1;i<=m;++i){st[e[i].l].push_back(e[i].r);}for(int i=1;i<=n;++i){if(st[i].empty())continue;cur.clear();for(auto &v:st[i])cur.insert(v);for(int j=1;j<=m;++j){if(e[j].l<i)continue;if(cur.lower_bound(e[j].l-1)!=cur.end()){int x=*cur.lower_bound(e[j].l-1);if(x<=e[j].r)cur.insert(e[j].r);}}ans+=cur.size();}printf("%lld\n",ans);}return 0;
}100分题解(分治+线段树+树状数组)
官解里有提到并查集维护区间并,没太想明白,所以开了四棵线段树
分治之后,左区间[l,mid],右区间[mid+1,r],
考虑如何统计跨左右区间的答案,即满足l<=L<=mid且mid+1<=R<=r的(L,R)答案
先定义点术语,方便下面描述:
左半区间:[l,mid]
右半区间:[mid+1,r]
左内区间:被完整包含于[l,mid]内的区间
右内区间:被完整包含于[mid+1,r]内的区间
跨域区间:左端点位于[l,mid],右端点位于[mid+1,r]的区间
从x走到y:存在一个区间[x,y],或存在若干个区间覆盖在一起,使得左端点是x,右端点y
若(L,R)合法, 换言之,从左端点L走到右端点R,有两种情况,
1. 存在跨域区间[L,R],一步从L走到R
2. ①L通过左内区间走若干步,走到[l,mid]内最靠右的位置,记为a[L]
②对称后,是相遇问题,R通过右内区间走若干步,走到[mid+1,r]最靠左的位置,记为a[R]
③L通过一个跨域区间(跨域区间左端点在[L,a[L]+1]内),走到[mid+1,r]内最靠左位置,记为b[L]
④R通过一个跨域区间(跨域区间右端点在[a[R]-1,R]内),走到[l,mid]内最靠右位置,记为b[R]
⑤[L,b[L]]和[b[R],R]两个区间,需要满足覆盖在一起后是[L,R],
因为,b[L]<=mid<mid+1<=b[R],所以,区间相交是自然满足的
还需满足b[L]<=R且L<=b[R],这是一个静态二维数点问题,可用树状数组或cdq分治解决
①-②步用了一棵线段树seg,区间查询,单点更新
左半边递减遍历维护最大值,右半边递增遍历维护最小值
③用了一棵线段树lseg,单点更新,维护左端点在[l,mid+1]内,右端点在右半区间的右端点最小值
④用了一棵线段树rseg,单点更新,维护右端点在[mid,r]内,左端点在左半区间的左端点最大值
[l,mid+1]是因为[L,a[L]+1],比如,[1,2]和[3,4]也可以覆盖[1,4];[mid,r]同理
因为③④区间有交集,且和①②维护的信息不同,所以各开了一棵线段树
外层已经是分治了,内层就不cdq分治了,⑤这里采用树状数组的方式解决
形如(L,b[L])和(b[R],R)的二维点对,按第一维排增序,
第一维相同时,先插入再查询,左半边插入到b[L]位置,右半边查询区间[b[R],R]
由于b[R]<=mid<b[L]恒成立,所以直接查sum(R)就可以
此外,注意到1和2的①②③④的情况,都不一定存在,所以需要分别判一下不存在的情况,
当然,如果用INF和-INF配合max min之后,能统一写法的话最好
分治为了使复杂度正确,每次使用完线段树之后需要手动回收,
对树状数组手动-1,撤销操作;对线段树[l,r]段区间删除打标记,
由于维护的是最大最小值,删除后,最大值为-INF,最小值为INF
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define SZ(x) (int)x.size()
#define fi first
#define se second
const int N=2e5+10,INF=0x3f3f3f3f;
int n,m,l,r,a[N],b[N];
vector<int>L[N],R[N];
ll ans;
struct segtree{int n;struct node{int l,r,c,mn,mx;}e[N<<2];#define l(p) e[p].l#define r(p) e[p].r#define c(p) e[p].c#define mn(p) e[p].mn#define mx(p) e[p].mxvoid up(int p){mn(p)=min(mn(p<<1),mn(p<<1|1));mx(p)=max(mx(p<<1),mx(p<<1|1));}void bld(int p,int l,int r){l(p)=l;r(p)=r;c(p)=0;if(l==r){mn(p)=INF;mx(p)=-INF;return;}int mid=l+r>>1;bld(p<<1,l,mid);bld(p<<1|1,mid+1,r);up(p);}void init(int _n){n=_n;bld(1,1,n);}void chg(int p,int x,int v){if(l(p)==r(p)){mn(p)=min(mn(p),v);mx(p)=max(mx(p),v);return;}int mid=l(p)+r(p)>>1;psd(p);chg(p<<1|(x>mid),x,v);up(p);}void psd(int p){if(c(p)){mn(p<<1)=INF;mx(p<<1)=-INF;c(p<<1)=c(p);mn(p<<1|1)=INF;mx(p<<1|1)=-INF;c(p<<1|1)=c(p);c(p)=0; }}void del(int p,int ql,int qr){if(ql<=l(p)&&r(p)<=qr){mn(p)=INF;mx(p)=-INF;c(p)=1;return;}psd(p);int mid=l(p)+r(p)>>1;if(ql<=mid)del(p<<1,ql,qr);if(qr>mid)del(p<<1|1,ql,qr);up(p);}int amn(int p,int ql,int qr){if(ql<=l(p)&&r(p)<=qr)return mn(p);int mid=l(p)+r(p)>>1,res=INF;psd(p);if(ql<=mid)res=min(res,amn(p<<1,ql,qr));if(qr>mid)res=min(res,amn(p<<1|1,ql,qr));return res;}int amx(int p,int ql,int qr){if(ql<=l(p)&&r(p)<=qr)return mx(p);int mid=l(p)+r(p)>>1,res=-INF;psd(p);if(ql<=mid)res=max(res,amx(p<<1,ql,qr));if(qr>mid)res=max(res,amx(p<<1|1,ql,qr));return res;}
}seg,lseg,rseg;
struct BitPre{int n,tr[N];void init(int _n){n=_n;memset(tr,0,(n+1)*sizeof(*tr));}void add(int x,int v){for(int i=x;i<=n;i+=i&-i)tr[i]+=v;}int ask(int x){if(x<0)return 0;int ans=0; for(int i=x;i;i-=i&-i)ans+=tr[i];return ans;}
}tr;
bool ok(int x){return x!=INF && x!=-INF;
}
bool in(int x,int l,int r){return l<=x && x<=r;
}
void cdq(int l,int r){if(l==r)return;int mid=(l+r)/2;cdq(l,mid);cdq(mid+1,r);for(int i=mid;i>=l;--i){a[i]=-INF;b[i]=INF;for(auto &v:L[i]){if(v>r)continue;if(v<=mid)a[i]=max(a[i],v);else b[i]=min(b[i],v);//有无需本侧的情况if(v>=mid)rseg.chg(1,v,i);}if(ok(a[i])){a[i]=max(a[i],seg.amx(1,i,min(mid,a[i]+1)));seg.chg(1,i,a[i]);}}for(int i=mid+1;i<=r;++i){a[i]=INF;b[i]=-INF;for(auto &v:R[i]){if(v<l)continue;if(v>=mid+1)a[i]=min(a[i],v);else b[i]=max(b[i],v);if(v<=mid+1)lseg.chg(1,v,i);}if(ok(a[i])){a[i]=min(a[i],seg.amn(1,max(mid+1,a[i]-1),i));seg.chg(1,i,a[i]);}}vector<array<int,3>>all;for(int i=mid;i>=l;--i){if(ok(a[i])){ // [i,a[i]+1]int v=lseg.amn(1,i,a[i]+1);if(in(v,mid+1,r)){b[i]=min(b[i],v);}}if(in(b[i],mid+1,r))all.push_back({i,0,b[i]});}for(int i=mid+1;i<=r;++i){if(ok(a[i])){ // [a[i]-1,i]int v=rseg.amx(1,a[i]-1,i);if(in(v,l,mid)){b[i]=max(b[i],v);}}if(in(b[i],l,mid))all.push_back({b[i],1,i});}sort(all.begin(),all.end());for(auto &w:all){int op=w[1],ub=w[2];if(op==0)tr.add(ub,1);else ans+=tr.ask(ub);//左[l,a[l]]右[a[r],r],满足l<=a[r]<=a[l]+1且a[r]-1<=a[l]<=r,a[l]<=mid<mid+1<=a[r]显然成立}seg.del(1,l,r);lseg.del(1,l,r);rseg.del(1,l,r);for(auto &w:all){int op=w[1],ub=w[2];if(op==0)tr.add(ub,-1);}
}
int main(){scanf("%d%d",&n,&m);seg.init(n);lseg.init(n);rseg.init(n);tr.init(n);for(int i=1;i<=m;++i){scanf("%d%d",&l,&r);//重复无所谓L[l].push_back(r);R[r].push_back(l);}cdq(1,n);printf("%lld\n",ans);return 0;
}
/*
9 4
1 4
1 8
3 9
2 5
*/写在最后
感觉数据结构有点多了,写起来比较疲惫
四五题连放两个数据结构,有点不太像之前csp的风格
反观之前的第三题大模拟,本次变成中模拟了
anyway,完结, 撒花!
相关文章:

CCF-CSP认证 202303 500分题解
202303-1 田地丈量(矩阵面积交) 矩阵面积交x轴线段交长度*y轴线段交长度 线段交长度,相交的时候是min右端点-max左端点,不相交的时候是0 #include<bits/stdc.h> using namespace std; int n,a,b,ans,x,y,x2,y2; int f(in…...

板内盘中孔设计狂飙,细密间距线路中招
一博高速先生成员:王辉东大风起兮云飞扬,投板兮人心舒畅。赵理工打了哈欠,伸了个懒腰,看了看窗外,对林如烟说道:“春天虽美,但是容易让人沉醉。如烟,快女神节了,要不今晚…...
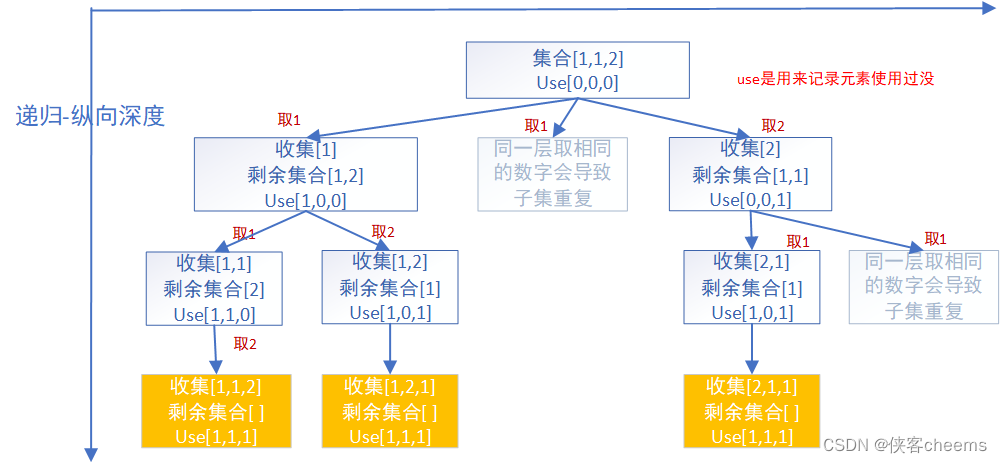
面试热点题:回溯算法 递增子序列与全排列 II
前言: 如果你一点也不了解什么叫做回溯算法,那么推荐你看看这一篇回溯入门,让你快速了解回溯算法的基本原理及框架 递增子序列 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两…...

怎么找回回收站删除的文件
我们都知道,电脑文件都是放在桌面上的,单独存放或者一起存放在文件夹里。但总会有已用完或者是没用的文件,这让我们不得不对其进行清理。而清空回收站也是不可避免的。如果出现了清空文件中还有我们需要的文件,怎么找回回收站删除…...

dp-打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非…...

C++预处理连接
目录定义常量字符串前缀定义枚举类型Boost C库中常常使用预处理连接来定义宏和模板类Google开源的C单元测试框架gtest,使用预处理连接技术创建测试用例和测试方法C预处理连接(Preprocessor Concatenation)是一种宏定义技巧,用于将…...

3、DRF实战总结:基于类的视图APIView, GenericAPIView和GenericViewSet视图集(附源码)
前面介绍了什么是符合RESTful规范的API接口,以及使用了基于函数的视图(FBV)编写了对文章进行增删查改的API。在本篇文章将使用基于类的视图(Class-based View, CBV)重写之前的接口。 参考: 1、Django开发总结:Django MVT与MVC设计模式&…...

AutoSAR PduR -AutoSAR PDU常用的使用方式【发送,接收,网关】
总目录链接==>> AutoSAR入门和实战系列总目录 @学前问答: AutoSAR PDU在哪里全局定义的? AutoSAR PDU涉及到哪些模块? AutoSAR PDU网关怎么使用? 文章目录 1 AutoSAR PDU发送2 AutoSAR PDU接收3 AutoSAR PDU网关转发4 答疑解析AutoSAR PDU 怎么样通过PduR 实现与其…...

瑟瑟发抖吧~OpenAI刚刚推出王炸——引入ChatGPT插件,开启AI新生态
5分钟学会使用ChatGPT 插件(ChatGPT plugins)——ChatGPT生态建设的开端ChatGPT插件是什么OpenAI最新官方blog资料表示,已经在ChatGPT中实现了对插件的初步支持。插件是专门为以安全为核心原则的语言模型设计的工具,可帮助ChatGPT…...

脉诊(切脉、诊脉、按脉、持脉)之法——入门篇
认识脉诊何谓脉诊?脉诊的渊源脉诊重要吗?脉诊确有其事,还是故弄玄虚?中医科学吗?如何脉诊?寸口脉诊法何谓脉诊? 所谓脉诊,就是通过把脉来诊断身体健康状况的一种必要手段。 …...

【十二天学java】day09常用api介绍
1.API 1.1API概述 什么是API API (Application Programming Interface) :应用程序编程接口 java中的API 指的就是 JDK 中提供的各种功能的 Java类,这些类将底层的实现封装了起来,我们不需要关心这些类是如何实现的,只需要学习这…...
软件测试 - 测试用例常见面试题
1.测试用例的要素测试用例是为了实施测试而向被测试的系统提供的一组集合, 这组集合包含 : 测试环境, 操作步骤, 测试数据, 预期结果等要素.例如 : 在 B 站输入框输入一个空格, 检查结果测试用例标题 : 输入框输入空格测试环境 : Windows 系统, 谷歌浏览器-版本 111.0.5563.65&…...

几种常见的API接口分页方案
文章目录1 概述2 分页方案2.1 基于偏移量2.2 基于游标3 重复数据处理3.1 基于时间3.2 基于热度3.3 基于推荐1 概述 列表是互联网产品中很常见的一种内容排列形式,而且列表的数据集往往成千上万,一次性返回全量数据集的场景几乎不存在,所以出…...

【Object 类的方法】
在 Java 中,所有类都继承了 Object 类,因此 Object 类中的方法可以在所有 Java 对象中使用。下面是 Object 类中的一些常用方法介绍: equals(Object obj): 用于判断两个对象是否相等。默认情况下,该方法比较的是两个对象的地址是…...

留用户、补内容,在线音乐暗战不停
在线音乐在人们的日常生活中扮演着愈发重要的角色,尤其是在面临巨大压力时,人们往往更倾向于通过倾听一段音乐来缓解内心的紧张与焦虑。而随着在线音乐用户数量的增长以及付费意愿的增强,在线音乐行业也实现了稳步发展。 经过多年的发展&…...

python--exec
在Python中,eval和exec都是用来执行动态代码的内置函数,但它们的作用和使用方式有所不同。 eval(): 将字符串作为Python表达式进行求值,并返回结果。 exec(): 将字符串作为Python语句进行执行,没有返回值。 eval()的使用范围通常限…...

干货分享!这6个高效率办公软件,总有一个值得你收藏!
分享6款高效办公软件,可以解决你很多需求,职场人一定要知道。每一款都是精挑细的,可能有的已经很大众了,但肯定还有小伙伴不知道,废话不多说,直接看!! 1、Flomo笔记:记录…...
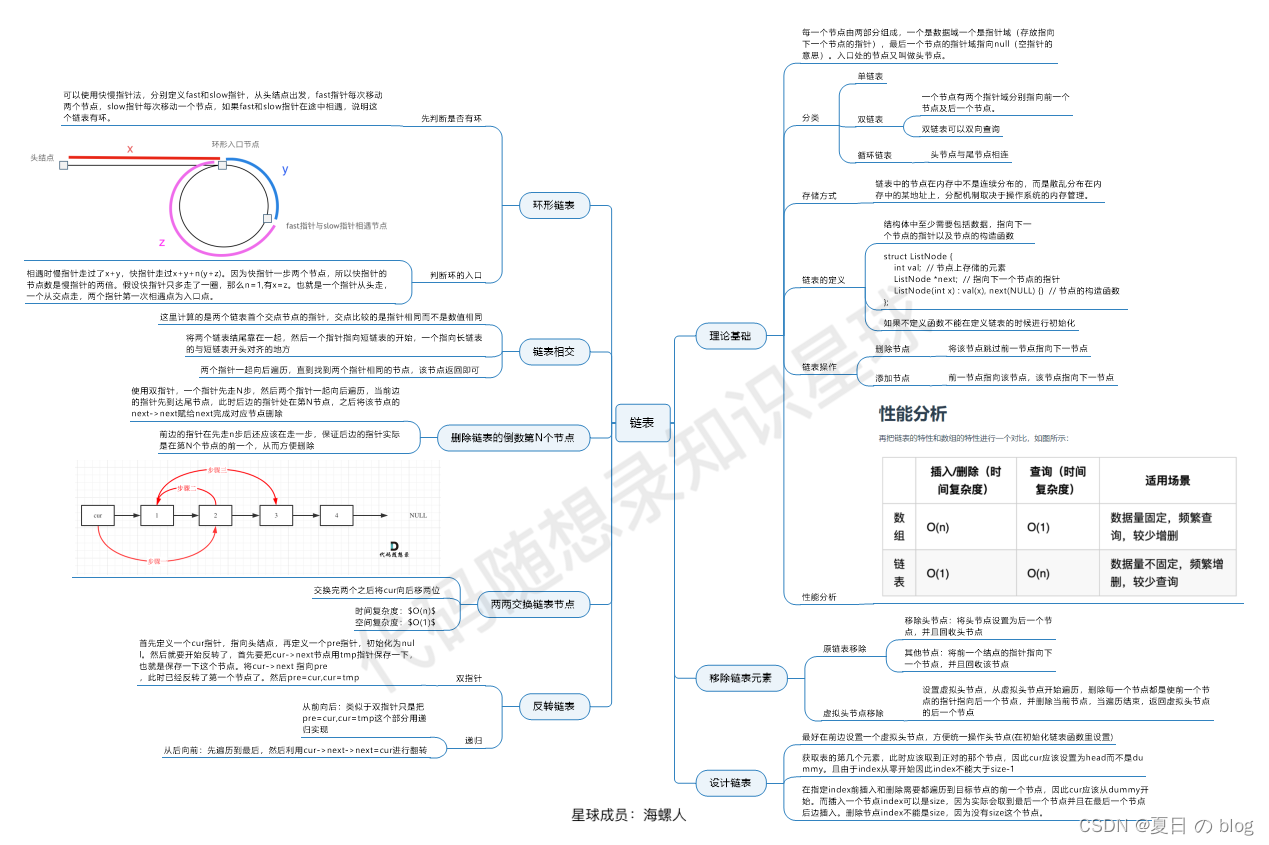
代码随想录刷题-链表总结篇
文章目录链表理论基础单链表双链表循环链表其余知识点链表理论基础单链表双链表循环链表其余知识点移除链表元素习题我的解法虚拟头结点解法设计链表习题我的解法代码随想录代码反转链表习题双指针递归两两交换链表中的节点习题我的解法代码随想录解法删除链表的倒数第N个节点习…...

C++:指针:什么是野指针
野指针目录1:定义2:野指针常见情形2.1 :未初始化的野指针2.2 所指的对象已经消亡2.3 指针释放之后未置空3:避免野指针1:定义 指向非法的内存地址的指针叫做野指针(Wild Pointer),也…...
一线大厂高并发Redis缓存架构
文章目录高并发缓存架构设计架构设计思路完整代码开发规范与优化建议键值设计命令使用客户端的使用扩展布隆过滤器redis的过期键的清除策略高并发缓存架构设计 架构设计思路 首先是一个基础的缓存架构,对于新增、修改操作set会对缓存更新,对于查询操作…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
