机器学习笔记之前馈神经网络(四)反向传播算法[数学推导过程]
机器学习笔记之前馈神经网络——反向传播算法[数学推导过程]
- 引言
- 回顾:感知机算法
- 非线性问题与多层感知机
- 反向传播算法(BackPropagation,BP\text{BackPropagation,BP}BackPropagation,BP)
- 场景构建
- 求解各权重更新量
- 图示描述反向传播过程
- 总结
引言
上一节介绍了M-P\text{M-P}M-P神经元模型,并介绍了感知机算法(Perceptron)(\text{Perceptron})(Perceptron)的参数调整过程。本节将介绍多层前馈神经网络,并介绍反向传播算法。
回顾:感知机算法
关于感知机算法,它本质上是一个仅包含一个M-P\text{M-P}M-P神经元的神经网络模型。以基本逻辑运算与为例,它们对应感知机算法的网络模型表示如下:
需要注意的是,这里的x1,x2x_1,x_2x1,x2是输入层,它们均表示‘样本特征的随机变量’,因而它们仅是‘接收外部信号的载体’,并不是M-P\text{M-P}M-P神经元模型。

对应计算流程表示如下:
Yout=f(W1⋅x1+W2⋅x2−θ)\mathcal Y_{out} = f \left(\mathcal W_1 \cdot x_1 + \mathcal W_2 \cdot x_2 - \theta \right)Yout=f(W1⋅x1+W2⋅x2−θ)
对于上述计算流程中的权重W1,W2\mathcal W_1,\mathcal W_2W1,W2和阈值θ\thetaθ,可将阈值θ\thetaθ视作一个固定输入的哑结点(Dummy Node\text{Dummy Node}Dummy Node)与对应权重的线性组合,从而使学习过程可统一为权重的学习过程:
Yout=f(W1⋅x1+W2⋅x2+WDum⋅xDum⏟Fixed)\mathcal Y_{out} = f(\mathcal W_1 \cdot x_1 + \mathcal W_2 \cdot x_2 + \mathcal W_{\text{Dum}} \cdot \underbrace{x_{\text{Dum}}}_{\text{Fixed}})Yout=f(W1⋅x1+W2⋅x2+WDum⋅FixedxDum)
关于感知机算法权重学习过程的参数调整使用梯度下降法。针对逻辑计算与,本质上是二分类问题。感知机算法关于策略的构建动机是策略驱动:
{LTrue(W)=∑(x(i),y(i))∈Dy^(i)(WTx(i))argmaxWLTrue(W){LFalse(W)=−∑(x(i),y(i))∈Dy(i)(WTx(i))argminWLFalse(W)\begin{aligned} & \begin{cases} \mathcal L_{\text{True}}(\mathcal W) = \sum_{(x^{(i)},y^{(i)}) \in \mathcal D} \hat y^{(i)} \left(\mathcal W^Tx^{(i)}\right) \\ \mathop{\arg\max}\limits_{\mathcal W} \mathcal L_{\text{True}}(\mathcal W) \end{cases} \\ & \begin{cases} \mathcal L_{\text{False}}(\mathcal W) = -\sum_{(x^{(i)},y^{(i)}) \in \mathcal D} y^{(i)} \left(\mathcal W^Tx^{(i)}\right) \\ \mathop{\arg\min}\limits_{\mathcal W} \mathcal L_{\text{False}}(\mathcal W) \end{cases} \\ \end{aligned}⎩⎨⎧LTrue(W)=∑(x(i),y(i))∈Dy^(i)(WTx(i))WargmaxLTrue(W)⎩⎨⎧LFalse(W)=−∑(x(i),y(i))∈Dy(i)(WTx(i))WargminLFalse(W)
关于感知机权重的调整过程可表示为:
W(t+1)⇐W(t)−η⋅∇WL(W)=W(t)−η⋅[∂LFalse(W)∂W+∂LTrue(W)∂W]=W(t)−η⋅∑(x(i),y(i))∈D(y^(i)−y(i))x(i)=W(t)+η⋅∑(x(i),y(i))∈D(y(i)−y^(i))x(i)\begin{aligned} \mathcal W^{(t+1)} & \Leftarrow \mathcal W^{(t)} - \eta \cdot \nabla_{\mathcal W} \mathcal L(\mathcal W) \\ & = \mathcal W^{(t)} - \eta \cdot \left[\frac{\partial \mathcal L_{\text{False}}(\mathcal W)}{\partial \mathcal W} + \frac{\partial \mathcal L_{\text{True}}(\mathcal W)}{\partial \mathcal W}\right] \\ & = \mathcal W^{(t)} - \eta \cdot \sum_{(x^{(i)},y^{(i)}) \in \mathcal D} \left(\hat y^{(i)} - y^{(i)}\right) x^{(i)} \\ & = \mathcal W^{(t)} + \eta \cdot \sum_{(x^{(i)},y^{(i)}) \in \mathcal D} \left(y^{(i)} - \hat y^{(i)}\right) x^{(i)} \end{aligned}W(t+1)⇐W(t)−η⋅∇WL(W)=W(t)−η⋅[∂W∂LFalse(W)+∂W∂LTrue(W)]=W(t)−η⋅(x(i),y(i))∈D∑(y^(i)−y(i))x(i)=W(t)+η⋅(x(i),y(i))∈D∑(y(i)−y^(i))x(i)
其中η\etaη表示学习率(Learning Rate\text{Learning Rate}Learning Rate)。关于迭代结束的标志:当关于样本特征x(i)x^{(i)}x(i)的预测结果y^(i)\hat y^{(i)}y^(i)与真实标签y(i)y^{(i)}y(i)相等,此时W(t)⇒W(t+1)\mathcal W^{(t)} \Rightarrow \mathcal W^{(t+1)}W(t)⇒W(t+1)不会发生变化,迭代可以停止。
非线性问题与多层感知机
在前馈神经网络——非线性问题中已经对解决非线性问题的方式进行了介绍,这里不再赘述。这里仅从M-P\text{M-P}M-P神经元模型的角度重温一下处理亦或问题的多层感知机结构:

很明显,这是一个两层感知机,其中包含输入层结点x1,x2x_1,x_2x1,x2,输出层结点Y\mathcal YY以及隐含层(Hidden Layer\text{Hidden Layer}Hidden Layer)结点h1,h2h_1,h_2h1,h2。
相比于感知机算法,上述多层感知机明显由333个M-P\text{M-P}M-P神经元模型嵌套组合的结构。并且神经元之间不存在同层连接,也不存在跨层连接。这种神经网络结构被称作多层前馈神经网络(Multi-Layer Feed-Forward Neural Network\text{Multi-Layer Feed-Forward Neural Network}Multi-Layer Feed-Forward Neural Network)。
以上述结构为例,输入层不算网络层数,因而上述结构被称作‘两层网络’。但如果将隐藏层、输出层区分开,也可以将其称作:单隐层网络。
上述模型需要学习的权重参数有:
Θ={W11,W12,W21,W22,θ1,θ2,θ3}\Theta = \{\mathcal W_{11},\mathcal W_{12},\mathcal W_{21},\mathcal W_{22},\theta_1,\theta_2,\theta_3\}Θ={W11,W12,W21,W22,θ1,θ2,θ3}
反向传播算法(BackPropagation,BP\text{BackPropagation,BP}BackPropagation,BP)
虽然上述的神经网络结构能够处理非线性问题,但关于权重参数Θ\ThetaΘ的学习过程,仅使用如错误驱动这种简单策略是不够的。
由于M-P\text{M-P}M-P神经元的嵌套,使得网络结构变得更加复杂,仅通过随机调整参数去观察y(i)−y^(i)y^{(i)} - \hat y^{(i)}y(i)−y^(i)的计算代价是极大的。
针对于多层神经网络,反向传播算法就是其中最杰出的代表。下面通过示例对梯度的反向传播过程进行描述。
场景构建
关于数据集合D\mathcal DD的描述表示如下:
这里为了泛化起见,并没有将标签y(i)(i=1,2,⋯,N)y^{(i)}(i=1,2,\cdots,N)y(i)(i=1,2,⋯,N)约束为标量,而是一个包含lll个随机变量的向量形式。
D={x(i),y(i)}i=1Nx(i)∈Rd;y(i)∈Rl\mathcal D = \{x^{(i)},y^{(i)}\}_{i=1}^N \quad x^{(i)} \in \mathbb R^{d};y^{(i)} \in \mathbb R^lD={x(i),y(i)}i=1Nx(i)∈Rd;y(i)∈Rl
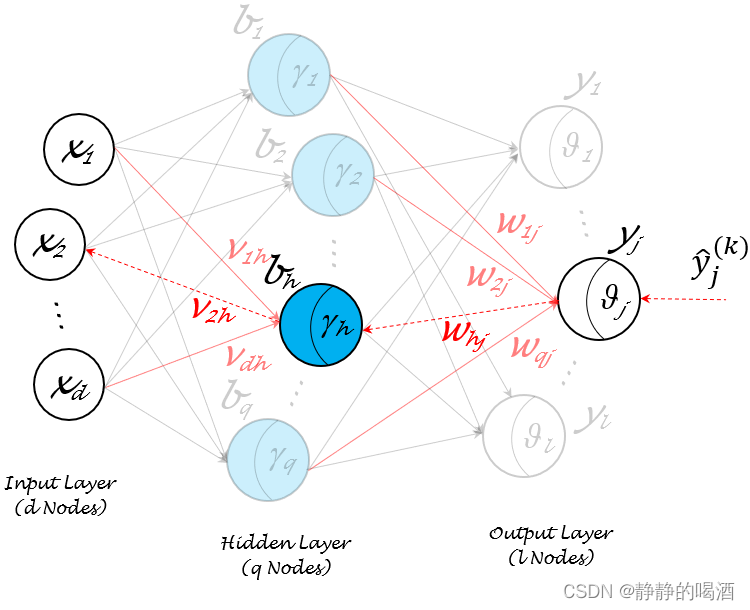
上述条件已经给出了输入层、输出层的规模分别是d,ld,ld,l,基于此构建一个含一个隐藏层的、隐藏层内神经元个数为qqq的单隐层前馈神经网络:

观察上图,除了输入层,隐藏层、输出层的结点均是M-P\text{M-P}M-P神经元模型:
- 其中隐藏层神经元的阈值分别表示为:{γ1,γ2,⋯,γq}\{\gamma_1,\gamma_2,\cdots,\gamma_q\}{γ1,γ2,⋯,γq};输出层神经元的阈值分别表示为:{θ1,θ2,⋯,θl}\{\theta_1,\theta_2,\cdots,\theta_l\}{θ1,θ2,⋯,θl};
- 输入层结点{x1,x2,⋯,xd}\{x_1,x_2,\cdots,x_d\}{x1,x2,⋯,xd}指向隐藏层第hhh个神经元bhb_hbh的权重分别表示为:{v1h,v2h,⋯,vdh}\{v_{1h},v_{2h},\cdots,v_{dh}\}{v1h,v2h,⋯,vdh};同理,隐藏层神经元{b1,b2,⋯,bq}\{b_1,b_2,\cdots,b_q\}{b1,b2,⋯,bq}指向输出层第jjj个神经元yjy_jyj的权重分别表示为:{w1j,w2j,⋯,wqj}\{w_{1j},w_{2j},\cdots,w_{qj}\}{w1j,w2j,⋯,wqj};
- 关于隐藏层神经元bhb_hbh接收到的输入αh\alpha_hαh可表示为:
αh=v1h⋅x1+⋯+vdh⋅xd=∑i=1dvih⋅xi\alpha_h = v_{1h} \cdot x_1 + \cdots + v_{dh} \cdot x_d = \sum_{i=1}^d v_{ih} \cdot x_iαh=v1h⋅x1+⋯+vdh⋅xd=i=1∑dvih⋅xi - 关于输出层神经元yjy_jyj接收到的输入βj\beta_jβj可表示为:
βj=w1j⋅b1+⋯+wqj⋅bq=∑i=1qwij⋅bi\beta_j = w_{1j} \cdot b_1 + \cdots + w_{qj} \cdot b_q = \sum_{i=1}^q w_{ij} \cdot b_iβj=w1j⋅b1+⋯+wqj⋅bq=i=1∑qwij⋅bi
这里假设隐藏层、输出层神经元使用Sigmoid\text{Sigmoid}Sigmoid函数作为激活函数。并以回归任务为例,针对某一具体样本(x(k),y(k))∈D(x^{(k)},y^{(k)}) \in \mathcal D(x(k),y(k))∈D进行计算。
求解各权重更新量
针对具体样本(x(k),y(k))(x^{(k)},y^{(k)})(x(k),y(k)),将样本特征x(k)=(x1(k),x2(k),⋯,xd(k))Tx^{(k)} = (x_1^{(k)},x_2^{(k)},\cdots,x_d^{(k)})^Tx(k)=(x1(k),x2(k),⋯,xd(k))T带入到神经网络中,从M-P\text{M-P}M-P神经元的角度观察,对应神经网络的输出y^(k)=(y^1(k),y^2(k),⋯,y^l(k))T\hat y^{(k)} = (\hat y_1^{(k)},\hat y_2^{(k)},\cdots,\hat y_l^{(k)})^Ty^(k)=(y^1(k),y^2(k),⋯,y^l(k))T表示为:
这里实际上描述的并不准确,因为βj,θj\beta_j,\theta_jβj,θj仅表示泛化的样本xxx作为输入层的输入,对应的接收结果和阈值。如果针对真实样本(x(k),y(k))(x^{(k)},y^{(k)})(x(k),y(k)),应该写作βj(k),θj(k)\beta_j^{(k)},\theta_j^{(k)}βj(k),θj(k),这里为了节约符号,直接用βj,θj\beta_j,\theta_jβj,θj替代。这里仅描述了神经元yjy_jyj的输出信息。
y^j(k)=f(βj−θj)=f(∑i=1qwij⋅bi−θj)j=1,2,⋯,l\hat y_j^{(k)} = f(\beta_j - \theta_j) = f \left(\sum_{i=1}^q w_{ij} \cdot b_i - \theta_j\right) \quad j=1,2,\cdots,ly^j(k)=f(βj−θj)=f(i=1∑qwij⋅bi−θj)j=1,2,⋯,l
由于是回归任务,因而这里使用 均方误差(Mean-Square Error,MSE\text{Mean-Square Error,MSE}Mean-Square Error,MSE)来描述神经网络输出y^(k)\hat y^{(k)}y^(k)与真实标签y(k)y^{(k)}y(k)之间的误差关系。关于(x(k),y(k))(x^{(k)},y^{(k)})(x(k),y(k))的误差结果E(k)\mathcal E^{(k)}E(k)表示如下:
这里由于只有111个样本,均值部分11\frac{1}{1}11就直接省略掉了。系数12\frac{1}{2}21仅是为后续求导便利使用。对其求解梯度过程中,仅改变梯度大小,梯度方向不会发生变化。
E(k)=12(y(k)−y^(k))2=12∑j=1l(yj(k)−y^j(k))2\begin{aligned} \mathcal E^{(k)} & = \frac{1}{2} (y^{(k)} - \hat y^{(k)})^2 \\ & = \frac{1}{2} \sum_{j=1}^l (y_j^{(k)} - \hat y_j^{(k)})^2 \end{aligned}E(k)=21(y(k)−y^(k))2=21j=1∑l(yj(k)−y^j(k))2
重新观察y^(k)\hat y^{(k)}y^(k),想通过上述神经网络得到一个具体预测结果,需要学习的权重有:
这里说的权重,包含阈值。
- 输入层与隐藏层之间所有连接的权重信息:一共q×dq \times dq×d个;
- 隐藏层与输出层之间所有连接的权重信息:一共q×lq \times lq×l个;
- 隐藏层自身的阈值数量:qqq个;
- 输出层自身的阈值数量:lll个;
总共包含(d+l+1)×q+l(d + l + 1) \times q + l(d+l+1)×q+l个权重需要学习。这里以输出层某神经元yjy_jyj与隐藏层某神经元bhb_hbh之间的连接权重Whj\mathcal W_{h_j}Whj为例,计算该权重的更新量:
需要注意的是,该操作仅仅是梯度下降的操作,而不是反向传播算法。
{Whj(t+1)=Whj(t)+△Whj(t)△Whj(t)=−η⋅∂E(k)∂Whj(t)\begin{cases} \mathcal W_{hj}^{(t+1)} = \mathcal W_{hj}^{(t)} + \triangle \mathcal W_{hj}^{(t)} \\ \triangle \mathcal W_{hj}^{(t)} = - \eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \mathcal W_{hj}^{(t)}} \end{cases}⎩⎨⎧Whj(t+1)=Whj(t)+△Whj(t)△Whj(t)=−η⋅∂Whj(t)∂E(k)
观察上图,Whj\mathcal W_{hj}Whj首先影响的是输出层的第jjj个M-P\text{M-P}M-P神经元yjy_jyj,基于神经元yjy_jyj接收到的输入是βj\beta_jβj,对应输出特征是y^j(k)\hat y_j^{(k)}y^j(k)。使用链式求导法则,将∂E(k)∂Whj(t)\frac{\partial \mathcal E^{(k)}}{\partial \mathcal W_{hj}^{(t)}}∂Whj(t)∂E(k)表示为如下形式:
∂E(k)∂Whj(t)=∂E(k)∂y^j(k)⋅∂y^j(k)∂βj⋅∂βj∂Whj(t)\frac{\partial \mathcal E^{(k)}}{\partial \mathcal W_{hj}^{(t)}} = \frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}} \cdot \frac{\partial \hat y_j^{(k)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial \mathcal W_{hj}^{(t)}}∂Whj(t)∂E(k)=∂y^j(k)∂E(k)⋅∂βj∂y^j(k)⋅∂Whj(t)∂βj
插一句,由于激活函数是Sigmoid\text{Sigmoid}Sigmoid函数,关于它的导数可以表示为如下形式:
f′(x)=[11+e−x]′=1+e−x−1[1+e−x]2=11+e−x⋅[1−11+e−x]=f(x)⋅[1−f(x)]\begin{aligned} f'(x) & = \left[\frac{1}{1 + e^{-x}}\right]' \\ & = \frac{1 + e^{-x} - 1}{\left[1 + e^{-x}\right]^2} \\ & = \frac{1}{1 + e^{-x}} \cdot \left[1 - \frac{1}{1 + e^{-x}}\right] \\ & = f(x) \cdot [1 - f(x)] \end{aligned}f′(x)=[1+e−x1]′=[1+e−x]21+e−x−1=1+e−x1⋅[1−1+e−x1]=f(x)⋅[1−f(x)]
因而关于链式求导法则中的各项表示如下:
- 第一项∂E(k)∂y^j(k)\begin{aligned}\frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}}\end{aligned}∂y^j(k)∂E(k):
将不含y^j(k)\hat y_j^{(k)}y^j(k)的项,视作常数。
∂E(k)∂y^j(k)=∂∂y^j(k)[12∑j=1l(yj(k)−y^j(k))2]=∂∂y^j(k){12[∑≠jl(yj(k)−y^j(k))2⏟=0+(yj(k)−y^j(k))2]}=∂∂y^j(k)[12(yj(k)−y^j(k))2]=−(yj(k)−y^j(k))\begin{aligned} \frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}} & = \frac{\partial}{\partial \hat y_j^{(k)}} \left[\frac{1}{2} \sum_{j=1}^l \left(y_j^{(k)} - \hat y_j^{(k)}\right)^2\right] \\ & = \frac{\partial}{\partial \hat y_j^{(k)}} \left\{\frac{1}{2} \left[\underbrace{\sum_{\neq j}^l \left(y_j^{(k)} - \hat y_j^{(k)}\right)^2}_{=0} + \left(y_j^{(k)} - \hat y_j^{(k)}\right)^2\right]\right\} \\ & = \frac{\partial}{\partial \hat y_j^{(k)}} \left[\frac{1}{2} \left(y_j^{(k)} - \hat y_j^{(k)}\right)^2\right] \\ & = -(y_j^{(k)} - \hat y_j^{(k)}) \end{aligned}∂y^j(k)∂E(k)=∂y^j(k)∂[21j=1∑l(yj(k)−y^j(k))2]=∂y^j(k)∂⎩⎨⎧21=0=j∑l(yj(k)−y^j(k))2+(yj(k)−y^j(k))2⎭⎬⎫=∂y^j(k)∂[21(yj(k)−y^j(k))2]=−(yj(k)−y^j(k)) - 第二项∂y^j(k)∂βj\begin{aligned}\frac{\partial \hat y_j^{(k)}}{\partial \beta_j}\end{aligned}∂βj∂y^j(k):
需要注意的点,不要将阈值忘掉,并且y^j(k)=Sigmoid(βj−θj)\hat y_j^{(k)} = \text{Sigmoid}(\beta_j - \theta_j)y^j(k)=Sigmoid(βj−θj)
∂y^j(k)∂βj=∂∂βj[Sigmoid(βj−θj)]=y^j(k)⋅[1−y^j(k)]\begin{aligned} \frac{\partial \hat y_j^{(k)}}{\partial \beta_j} & = \frac{\partial}{\partial \beta_j} \left[\text{Sigmoid}(\beta_j - \theta_j)\right] \\ & = \hat y_j^{(k)} \cdot \left[1 - \hat y_j^{(k)}\right] \end{aligned}∂βj∂y^j(k)=∂βj∂[Sigmoid(βj−θj)]=y^j(k)⋅[1−y^j(k)] - 第三项∂βj∂Whj\begin{aligned}\frac{\partial \beta_j}{\partial \mathcal W_{hj}}\end{aligned}∂Whj∂βj。根据βj\beta_jβj与Whj\mathcal W_{hj}Whj之间的关系:
其中只有一项Whj⋅bh\mathcal W_{hj} \cdot b_hWhj⋅bh和Whj\mathcal W_{hj}Whj相关.
βj=∑i=1qWij⋅bi=W1j⋅b1+⋯+Whj⋅bh+⋯+Wqj⋅bq\begin{aligned} \beta_j & = \sum_{i=1}^q \mathcal W_{ij} \cdot b_i \\ & = \mathcal W_{1j}\cdot b_1 + \cdots + \mathcal W_{hj} \cdot b_h + \cdots + \mathcal W_{qj} \cdot b_q \end{aligned}βj=i=1∑qWij⋅bi=W1j⋅b1+⋯+Whj⋅bh+⋯+Wqj⋅bq
因而有:
∂βj∂Whj=bh\begin{aligned} \frac{\partial \beta_j}{\partial \mathcal W_{hj}} = b_h \end{aligned}∂Whj∂βj=bh
至此,关于Whj\mathcal W_{hj}Whj的更新量△Whj\triangle \mathcal W_{hj}△Whj可表示为:
△Whj=−η⋅∂E(k)∂Whj=−η⋅∂E(k)∂y^j(k)⋅∂y^j(k)∂βj⋅∂βj∂Whj(t)=−η⋅[−(yj(k)−y^j(k))]⋅y^j(k)⋅[1−y^j(k)]⋅bh=η⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))⋅bh\begin{aligned} \triangle \mathcal W_{hj} & = - \eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \mathcal W_{hj}} \\ & = -\eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}} \cdot \frac{\partial \hat y_j^{(k)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial \mathcal W_{hj}^{(t)}} \\ & = - \eta \cdot \left[-(y_j^{(k)} - \hat y_j^{(k)})\right] \cdot \hat y_j^{(k)} \cdot \left[1 - \hat y_j^{(k)}\right] \cdot b_h \\ & = \eta \cdot \hat y_j^{(k)} \cdot (1 - \hat y_j^{(k)})\cdot(y_j^{(k)} - \hat y_j^{(k)}) \cdot b_h \end{aligned}△Whj=−η⋅∂Whj∂E(k)=−η⋅∂y^j(k)∂E(k)⋅∂βj∂y^j(k)⋅∂Whj(t)∂βj=−η⋅[−(yj(k)−y^j(k))]⋅y^j(k)⋅[1−y^j(k)]⋅bh=η⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))⋅bh
同理,其他权重更新量△θj,△γh,△vih(k)\triangle \theta_j,\triangle \gamma_h,\triangle v_{ih}^{(k)}△θj,△γh,△vih(k)的求解过程分别表示为:
- θj\theta_jθj的权重更新量△θj\triangle \theta_j△θj:
θj\theta_jθj和△Whj\triangle \mathcal W_{hj}△Whj仅相差一个−bh-b_h−bh项.
△θj=−η⋅∂E(k)∂θj=−η⋅∂E(k)∂y^j(k)⋅∂y^j(k)∂θj=−η⋅[−(yj(k)−y^j(k))]⋅y^j(k)⋅(1−y^j(k))⋅(0−1)=−η⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))\begin{aligned} \triangle\theta_j & = -\eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \theta_j} \\ & = -\eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}} \cdot \frac{\partial \hat y_j^{(k)}}{\partial \theta_j} \\ & = - \eta \cdot \left[-(y_j^{(k)} - \hat y_j^{(k)})\right] \cdot \hat y_j^{(k)} \cdot \left(1 - \hat y_j^{(k)}\right) \cdot (0-1) \\ & = - \eta \cdot \hat y_j^{(k)} \cdot (1 - \hat y_j^{(k)})\cdot(y_j^{(k)} - \hat y_j^{(k)}) \\ \end{aligned}△θj=−η⋅∂θj∂E(k)=−η⋅∂y^j(k)∂E(k)⋅∂θj∂y^j(k)=−η⋅[−(yj(k)−y^j(k))]⋅y^j(k)⋅(1−y^j(k))⋅(0−1)=−η⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k)) - γh\gamma_hγh的权重更新量△γh\triangle \gamma_h△γh:
其中bh(k)b_h^{(k)}bh(k)表示隐藏层的输出,其与αh,γh\alpha_h,\gamma_hαh,γh之间的关系如下:
bh(k)=Sigmoid(αh−γh)=Sigmoid(∑i=1dvih(k)⋅xi(k))\begin{aligned} b_h^{(k)} & = \text{Sigmoid}(\alpha_h - \gamma_h) \\ & = \text{Sigmoid} \left(\sum_{i=1}^d v_{ih}^{(k)} \cdot x_i^{(k)}\right) \end{aligned}bh(k)=Sigmoid(αh−γh)=Sigmoid(i=1∑dvih(k)⋅xi(k))
同上,关于隐藏层第hhh个神经元的阈值γh\gamma_hγh具体是指γh(k)\gamma_h^{(k)}γh(k),这里为简化符号,不做修改.
并且隐藏层神经元输出bhb_hbh与输出层的所有神经元之间均存在关联关系,因此需要加上∑j=1l\sum_{j=1}^l∑j=1l.
△γh=−η⋅∂E(k)∂γh=−η⋅∂E(k)∂bh(k)⋅∂bh(k)∂γh=−η⋅∑j=1l(∂E(k)∂y^j(k)⋅∂y^j(k)∂βj⋅∂βj∂bh(k))⋅∂bh(k)∂γh=−η⋅∑j=1ly^j(k)⋅(1−y^j(k))⋅[−(yj(k)−y^j(k))]⋅Whj⋅[−bh⋅(1−bh)]=−η⋅[bh⋅(1−bh)]⋅∑j=1l[Whj⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))]\begin{aligned} \triangle \gamma_h &= -\eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \gamma_h} \\ & = -\eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial b_h^{(k)}} \cdot \frac{\partial b_h^{(k)}}{\partial \gamma_h} \\ & = -\eta \cdot \sum_{j=1}^l\left(\frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}} \cdot \frac{\partial \hat y_j^{(k)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h^{(k)}}\right) \cdot \frac{\partial b_h^{(k)}}{\partial \gamma_h} \\ & = -\eta \cdot \sum_{j=1}^l \hat y_j^{(k)} \cdot \left(1 - \hat y_j^{(k)}\right)\cdot \left[-(y_j^{(k)} - \hat y_j^{(k)})\right] \cdot \mathcal W_{hj} \cdot \left[-b_h \cdot (1 - b_h)\right] \\ & = - \eta \cdot [b_h \cdot(1 -b_h)] \cdot \sum_{j=1}^l \left[\mathcal W_{hj} \cdot \hat y_j^{(k)} \cdot (1 - \hat y_j^{(k)})\cdot (y_j^{(k)} - \hat y_j^{(k)})\right] \end{aligned}△γh=−η⋅∂γh∂E(k)=−η⋅∂bh(k)∂E(k)⋅∂γh∂bh(k)=−η⋅j=1∑l(∂y^j(k)∂E(k)⋅∂βj∂y^j(k)⋅∂bh(k)∂βj)⋅∂γh∂bh(k)=−η⋅j=1∑ly^j(k)⋅(1−y^j(k))⋅[−(yj(k)−y^j(k))]⋅Whj⋅[−bh⋅(1−bh)]=−η⋅[bh⋅(1−bh)]⋅j=1∑l[Whj⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))] - vih(k)v_{ih}^{(k)}vih(k)的权重更新量△vih(k)\triangle v_{ih}^{(k)}△vih(k):
需要注意的点:∂bh(k)∂αh\begin{aligned}\frac{\partial b_h^{(k)}}{\partial \alpha_h}\end{aligned}∂αh∂bh(k)与∂bh(k)∂γh\begin{aligned}\frac{\partial b_h^{(k)}}{\partial \gamma_h}\end{aligned}∂γh∂bh(k)都是Sigmoid\text{Sigmoid}Sigmoid函数的导数,只不过差一个负号;∂y^j(k)∂βj\begin{aligned}\frac{\partial \hat y_j^{(k)}}{\partial \beta_j}\end{aligned}∂βj∂y^j(k)和∂y^j(k)∂θj\begin{aligned}\frac{\partial \hat y_j^{(k)}}{\partial \theta_j}\end{aligned}∂θj∂y^j(k)也是如此。
△vih(k)=−η⋅∂E(k)∂vih(k)=−η⋅∂E(k)∂αh⋅∂αh∂vih(k)=−η⋅∑j=1l(∂E(k)∂y^j(k)⋅∂y^j(k)∂βj⋅∂βj∂bh(k)⋅∂bh(k)∂αh)⋅∂αh∂vih(k)=η⋅[bh⋅(1−bh)]⋅∑j=1l[Whj⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))]⋅xi(k)\begin{aligned} \triangle v_{ih}^{(k)} & = - \eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial v_{ih}^{(k)}} \\ & = -\eta \cdot \frac{\partial \mathcal E^{(k)}}{\partial \alpha_h} \cdot \frac{\partial \alpha_h}{\partial v_{ih}^{(k)}} \\ & = -\eta \cdot \sum_{j=1}^l \left( \frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}} \cdot \frac{\partial \hat y_{j}^{(k)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h^{(k)}} \cdot \frac{\partial b_h^{(k)}}{\partial \alpha_h}\right) \cdot \frac{\partial \alpha_h}{\partial v_{ih}^{(k)}} \\ & = \eta \cdot [b_h \cdot(1 -b_h)] \cdot \sum_{j=1}^l \left[\mathcal W_{hj} \cdot \hat y_j^{(k)} \cdot (1 - \hat y_j^{(k)})\cdot (y_j^{(k)} - \hat y_j^{(k)})\right] \cdot x_i^{(k)} \end{aligned}△vih(k)=−η⋅∂vih(k)∂E(k)=−η⋅∂αh∂E(k)⋅∂vih(k)∂αh=−η⋅j=1∑l(∂y^j(k)∂E(k)⋅∂βj∂y^j(k)⋅∂bh(k)∂βj⋅∂αh∂bh(k))⋅∂vih(k)∂αh=η⋅[bh⋅(1−bh)]⋅j=1∑l[Whj⋅y^j(k)⋅(1−y^j(k))⋅(yj(k)−y^j(k))]⋅xi(k)
图示描述反向传播过程
假设第ttt次迭代隐藏层神经元bhb_hbh、输出层神经元yjy_jyj的正向执行过程表示如下:
依然以某一具体样本(x(k),y(k))∈D(x^{(k)},y^{(k)}) \in \mathcal D(x(k),y(k))∈D,并以预测结果的第jjj个分量yj(k)y_j^{(k)}yj(k)的反向传播作为示例进行描述.
{αh=∑i=1dvih(k)⋅xi(k)bh(k)=Sigmoid(αh−γh)βj=∑h=1qWhj⋅bhy^j(k)=Sigmoid(βj−θj)\begin{aligned} \begin{cases} \alpha_h = \sum_{i=1}^d v_{ih}^{(k)} \cdot x_i^{(k)} \\ b_h^{(k)} = \text{Sigmoid}(\alpha_h - \gamma_h) \\ \beta_j = \sum_{h=1}^q \mathcal W_{hj} \cdot b_h \\ \hat y_j^{(k)} = \text{Sigmoid}(\beta_j - \theta_j) \end{cases} \end{aligned}⎩⎨⎧αh=∑i=1dvih(k)⋅xi(k)bh(k)=Sigmoid(αh−γh)βj=∑h=1qWhj⋅bhy^j(k)=Sigmoid(βj−θj)
- 首先,针对预测结果y^j(k)\hat y_j^{(k)}y^j(k)和真实标签yj(k)y_j^{(k)}yj(k)之间的误差结果对y^j(k)\hat y_j^{(k)}y^j(k)的梯度∂E(k)∂y^j(k)\begin{aligned}\frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}}\end{aligned}∂y^j(k)∂E(k)进行计算:

- 梯度∂E(k)∂y^j(k)\begin{aligned}\frac{\partial \mathcal E^{(k)}}{\partial \hat y_j^{(k)}}\end{aligned}∂y^j(k)∂E(k)计算完成后,神经元yjy_jyj获取相应梯度,将该梯度传递给阈值θj\theta_jθj以及各隐藏层神经元与yjy_jyj的连接权重∂E(k)∂θj,∂E(k)∂Whj(k)\begin{aligned}\frac{\partial \mathcal E^{(k)}}{\partial \theta_j},\frac{\partial \mathcal E^{(k)}}{\partial \mathcal W_{hj}^{(k)}}\end{aligned}∂θj∂E(k),∂Whj(k)∂E(k):
这里以隐藏层神经元bhb_hbh为关注点描述反向传播过程,因而仅点亮一条连接权重Whj\mathcal W_{hj}Whj;但实际上与yjy_jyj相关联的权重均被点亮。

- 传递到神经元bhb_hbh后,首先对该神经元的预测结果bh(k)b_h^{(k)}bh(k)求解梯度;紧接着对神经元的阈值γh\gamma_hγh和连接权重αh\alpha_hαh求解梯度∂E(k)∂bh(k),∂E(k)∂γh,∂E(k)∂αh\begin{aligned}\frac{\partial \mathcal E^{(k)}}{\partial b_h^{(k)}},\frac{\partial \mathcal E^{(k)}}{\partial \gamma_h},\frac{\partial \mathcal E^{(k)}}{\partial \alpha_h}\end{aligned}∂bh(k)∂E(k),∂γh∂E(k),∂αh∂E(k):

最终,当梯度传递至αh\alpha_hαh后,对输入层与隐藏层的连接权重求解梯度∂E(k)∂vih(k)\begin{aligned}\frac{\partial \mathcal E^{(k)}}{\partial v_{ih}^{(k)}}\end{aligned}∂vih(k)∂E(k):
这里以i=2i=2i=2为例,实际上所有与神经元bhb_hbh相关联的权重均被点亮。
至此,经过上述过程后,所有神经元结点以及相关权重,均更新了梯度。而且该示例中每个隐藏层的神经元结点每次计算过程中均更新了lll次权重,这与下一层结点(这里是指输出层结点)数量相关。
下一次迭代(t+1t+1t+1)使用更新后的权重参数进行正向传播过程。
总结
总观反向传播算法,实际上就是一个链式求导法则的工具:
- 它自身没有具体的目标函数/策略,这里的目标函数是均方误差E(k)(k=1,2,⋯,N)\mathcal E^{(k)}(k=1,2,\cdots,N)E(k)(k=1,2,⋯,N)提供的;
- 它自身也不属于算法,这里的算法(更新量的作用,使用学习率η\etaη)是梯度下降法;
因此,反向传播算法是将传播过程的更新量计算出来,其余操作并未参与。因而,它并不算是真正意义上的算法,它的迭代次数是人为决定的;它自身也不存在收敛性。
相关参考:
机器学习(周志华著)
相关文章:

机器学习笔记之前馈神经网络(四)反向传播算法[数学推导过程]
机器学习笔记之前馈神经网络——反向传播算法[数学推导过程]引言回顾:感知机算法非线性问题与多层感知机反向传播算法(BackPropagation,BP\text{BackPropagation,BP}BackPropagation,BP)场景构建求解各权重更新量图示描述反向传播过程总结引言 上一节介绍了M-P\tex…...

vscode+elementui校园跑腿系统 nodejs+vue
本系统从用户的角度出发,结合当前的校园环境而开发的,在开发语言上是使用的Java语言,在框架上我们是使用的Vue框架,数据库方面使用的是MySQL数据库,开发工具为IDEA。 基于Vue的校园跑腿管理系统中的管理员配送用户都可…...

[蓝桥杯单片机8]定时器的简单应用
1、本实验内容 利用51单片机的定时/计数器T0的模式1实现间隔定时,每隔1秒L1指示灯闪烁一下,也就是点亮0.5秒,熄灭0.5秒;每隔2秒L8指示灯闪烁一下,即点亮1秒,熄灭1秒。2、基础知识 定时/计数器,是…...

node-HTTP协议
文章目录一. 概念二. 请求报文的组成三.HTTP请求行四.HTTP请求头五.HTTP的请求体六.响应报文的组成七.创建HTTP服务八.获取HTTP请求报文九.HTTP设置响应十.GET和POST请求的区别一. 概念 HTTP协议. 中文叫超文本传输协议; 是一种基于TCP/IP的应用层通信协议; 这个协议详细规定了…...
基于springboot+vue的地方美食分享网站
081-springboot基于vue的地方美食分享网站开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&am…...

【Android】之【Aplication】
一、Application简介 Application和Activity,Service一样是Android框架的一个系统组件,当Android程序启动时系统会创建一个Application对象,用来存储系统的一些信息。 Android系统自动会为每个程序运行时创建一个Application类的对象且只创建…...

社区之声|Grant Program支持Moonbeam生态壮大
在本次社区之声会议中,Moonbeam基金会解释生态系统Grant流程、一个由社区成员组成的圆桌讨论表达各自对此次Grant的看法,Moonbeam开发者关系工程师演示了如何在Snapshot对申请生态系统Grant项目的投票。观看视频回顾 请注意,内容仅供参考&am…...
)
GO实现Redis:GO实现Redis协议解析器(2)
本文实现Redis的协议层,协议层负责解析指令,然后将指令交给核心database执行echo database用来测试协议层的代码https://github.com/csgopher/go-redis RESP协议 RESP是客户端与服务端通信的协议,格式有五种:正常回复࿱…...
Geoserver 发布wmts服务,以及cesium加载发布的wmts服务
WMTS提供了一种采用预定义图块方法发布数字地图服务的标准化解决方案。WMTS弥补了WMS不能提供分块地图的不足。WMS针对提供可定制地图的服务,是一个动态数据或用户定制地图(需结合SLD标准)的理想解决办法。WMTS牺牲了提供定制地图的灵活性&am…...
【微信小程序】selectComponent(#id)失败得到是null分析
小程序中无法像网页中轻易的获取DOM元素,需要依靠 this.selectComponent(#id)this.selectAllComponents(#id) 本文主要针对 this.selectComponent 获取DOM元素失败的原因 下面开始正文 上图为我的业务代码,由图可知,通过for循环遍历渲染ca…...
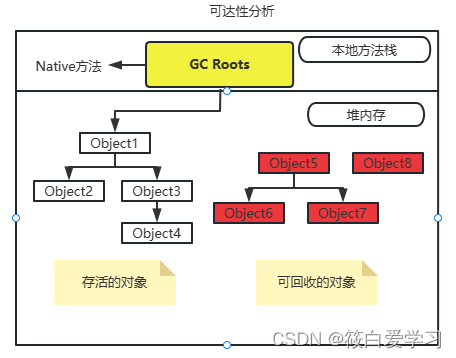
JVM中引用计数法与可达性分析
目录 概要 如何判断对象已死? 引用计数算法 优点 缺点 举例说明 可达性分析 图例说明 GC Roots的对象包括以下几种 可达性分析回收过程 四大引用 回收方法区 方法区的垃圾收集主要回收两部分内容: 1. 废弃的常量 2. 不再使用的类型。 JVM是…...

JS-对象篇
内容 简单介绍 重点介绍三个 Array,String和JSON 后面这两个不是重点 BOM-浏览器对象模型 DOM-文档对象模式(JS中每个HTML标签都封装成一个DOM对象) Array 和java不同 方式一 JS中是var 变量 new Array()(这个变量名后面没有[]这个标记&…...

【Unity】创建一个自己的AR安卓程序
目录1 环境配置2 下载官方提供的AR Starter工程3 AR Starter工程中的包以及打包设置3.1 Package Manager3.2 Player Settings4 创建一个新的AR场景5 AR场景中的物体6 在unity中运行AR场景7 在AR场景的基础上添加自己的想法7.1 修改Cube的旋转速度/方向7.2 将Cube替换为其他物体…...

游戏平台商店化的功能特点
帮助用户高效的获取游戏以及游戏相关内容是游戏平台的核心,基于这个需求在平台功能的设计上与其他类型产品也有着类似的思路。商店模式的特点诸如百货商店、超市、书店以及其他类型的商店,都会根据推荐、分类两个特点提供商品。 如果把游戏比作书籍&…...
)
最新前端面试知识点总结-2023(3w+字,长篇幅)
2023-前端面试知识点总结面试题总览javascript相关一、js 代码的常用优化手段二、es5 构造函数与继承三、new 一个对象的过程四、防抖与节流五、promise/A规范概述六、实现一个柯里函数封装七、事件队列八、微任务是哪些宏任务是哪些九、执行js代码时,同步任务、微任…...

离线安装ffmpeg
linux离线安装ffmpeg 获取安装包:[ffmpeg-release](Index of /releases (ffmpeg.org)) 下载最新版本,ffmpeg-4.4.tar.gz 然后传送到服务器上,解压安装 # 解压 tar -zxvf ffmpeg-4.4.tar.gz# 安装 cd ffmpeg-4.4 ./configure --enable-sha…...

位置编码Positional Encoding
位置编码Positional Encoding1.Transformers中的PE2.什么是Transformer位置编码2.1.表格型2.2.相对位置的关系-函数型3.为什么可以表示相对距离?4.其他参考内容全来自于网络总结。 其他参考1其他参考2 1.Transformers中的PE 摘抄自这里。 公式是初中生都看的懂, …...
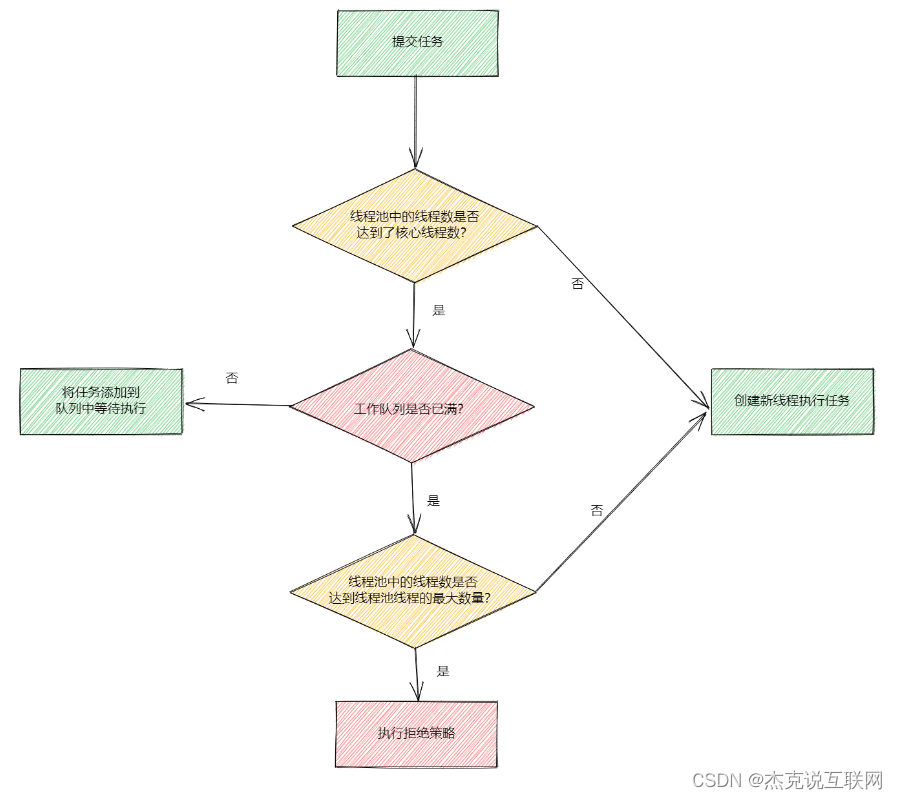
Java异步注解@Async详解
一、Async注解 Async的作用就是异步处理任务。 在方法上添加Async,表示此方法是异步方法;在类上添加Async,表示类中的所有方法都是异步方法;使用此注解的类,必须是Spring管理的类;需要在启动类或配置类中…...
macOS Big Sur 11.7.5 (20G1225) 正式版 ISO、PKG、DMG、IPSW 下载
本站提供的 macOS Big Sur 软件包,既可以拖拽到 Applications(应用程序)下直接安装,也可以制作启动 U 盘安装,或者在虚拟机中启动安装。 2023 年 3 月 27 日 (北京时间 28 日凌晨),…...

硬件语言Verilog HDL牛客刷题day02 组合逻辑部分
1.VL11 4位数值比较器电路 1.题目: 某4位数值比较器的功能表如下。请用Verilog语言采用门级描述方式,实现此4位数值比较器。 2.解题代码: timescale 1ns/1nsmodule comparator_4(input [3:0] A ,input [3:0] B ,output …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
