【统计模型】某地区土壤所含可给态磷回归分析

目录

某地区土壤所含可给态磷回归分析

一、研究目的

二、数据来源和相关说明

三、描述性分析

3.1 样本描述

3.2 数据可视化

四、数据建模

4.1 回归模型A

4.2 回归模型B

4.3 回归模型B模型诊断

4.4 回归模型C

五、结论及建议

5.1 结论

5.2 建议

六、代码

---

某地区土壤所含可给态磷回归分析

摘要： 本文建立了多个回归模型，分析土壤内可给态磷影响因素。经过分析得出土壤内可给态林浓度主要与土壤内无机磷浓度、土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷有关，且前者对可给态磷浓度影响较大。逐步回归模型满足正态性与方差齐性，且通过了显著性检验。根据土壤内无机磷浓度增加的0-1变量对土壤内可给态磷浓度不存在显著性影响。基于此，可以根据回归方程模型，对玉米的生产与产量起到指导意义。

一、研究目的

结合土壤中可给态磷的浓度，可以预测玉米体内可供态磷浓度的状态，预测玉米的生长态势，指导玉米生产；另一方面，可以求出土壤中无机磷浓度被期望的范围，从而对改善玉米的土壤条件，对提高玉米产量起到重要作用。结合此背景，本文欲分析某地区土壤所含可给态磷的影响因素，进而对提出合理化建议。

二、数据来源和相关说明

本文依据表1某地区土壤所含可给态磷的情况，建立多元线性回归方程。数据共计18条，涉及4个变量，分别是：

表 2-1  变量说明

变量	解释
X1	土壤内所含无机磷浓度
X2	土壤内溶于K2CO3溶液并受溴化物水解的有机磷
X3 X4	土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷 以变量X1中位数为分界点，将X1化为0-1变量
Y	一种在20℃土壤内的玉米中的可给态磷

三、描述性分析

为了获取对数据的直观了解，本文先对数据进行了描述性统计分析。

3.1 样本描述

表 3-1  样本描述

	MEAN	SD	MIN	MED	MAX
X1	11.94	10.15	0.40	10.50	29.90
X2	42.06	13.58	19.00	44.00	65.00
X3	123.00	45.74	37.00	123.50	202.00
Y	81.28	27.00	51.00	77.00	168.00

      从表3-1可以得出：土壤内所含无机磷浓度（X1）介于0.40-29.90之间，其平均水平约为11.94（平均值）和10.50（中位数），变异水平约为10.15（标准差）；土壤内溶于K2CO3溶液并受溴化物水解的有机磷（X2）介于19.00-65.00之间，其平均水平约为42.06（平均值）和44.00（中位数），变异水平约为13.58（标准差）；土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷（X3）介于37.00-202.00之间，其平均水平约为123.00（平均值）和123.50（中位数），变异水平约为45.74（标准差）；一种在20℃土壤内的玉米中的可给态磷（Y）介于51.00-168.00之间，其平均水平约为81.28（平均值）和77.00（中位数），变异水平约为27.00（标准差）。

3.2 数据可视化

      为了更直观分析数据分布情况与数据间的相关关系，本文绘制了各个变量的直方图与各变量的相关性热力图，结果如图3-1和3-2所示。

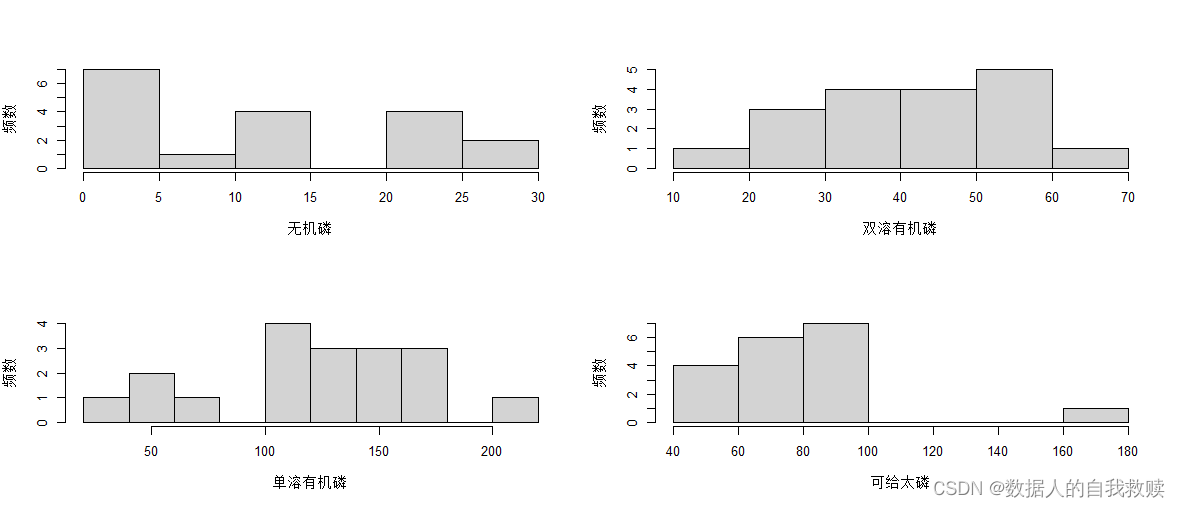
图 3-1  直方图

      从图3-1可以得出：四个均不服从正态分布，其中无机磷（X1）浓度主要集中在0~5；土壤内溶于K2CO3溶液并受溴化物水解的有机磷（X2）浓度主要集中在30-60；土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷（X3）浓度主要集中在100-175；可给态磷浓度（Y）主要集中在60-100。

图 3-2  相关性热力图

      由图3-2可以得出：变量X1与Y之间存在较强的线性相关关系，变量X2、X3与Y之间的线性相关关系较弱。

四、数据建模

4.1 回归模型A

      为了分析可给态磷浓度（Y）的影响因素，本文首先建立了全部变量的多元线性回归方程A，即以Y作为因变量，X1-X3作为自变量，建立线性回归方程：

Y=β0+β1X1+β2X2+β3X3+ϵ

模型结果如表4-1所示。

表 4-1  回归模型A结果

	Estimate	Std.Error	t value	Pr(>|t|)
(Intercept)	43.650	18.054	2.418	0.030*
X1	1.785	0.540	3.308	0.052**
X2	-0.083	0.420	-0.198	0.846
X3	0.161	0.112	1.443	0.171
R-squared	0.5493
Adjusted R-squared	0.4527
p-value	0.009227

      从表4-1可以得出：在显著性水平α=0.05 下，三个变量中，只有X1的P值<0.05，即对Y有显著影响，而变量X2和X3的P值>0.05，即对Y不存在显著性影响。模型的检验P值为0.009<0.05，即通过检验，说明方程具有统计学意义。

4.2 回归模型B

      由于模型A中X2和X3对Y不存在显著性影响，因而本文又建立了逐步回归模型B，对自变量进行选择，模型结果如表4-2所示。

表4-2 回归模型B结果

	Estimate	Std.Error	t value	Pr(>|t|)
(Intercept)	41.479	13.883	2.988	0.009**
X1	1.737	0.467	3.721	0.002**
X3	0.155	0.104	1.494	0.156
R-squared	0.5481
Adjusted R-squared	0.4878
p-value	0.002589

      由表4-2可以得出：经过逐步回归分析，剔除了变量X2，保留了变量X1和X3。模型P值为0.003<0.05，通过检验。回归方程为：

Y=41.479+1.737X1+0.155X3     (1)

即X1每增加1，因变量Y增加1.737；X3每增加1，因变量Y增加0.155，自变量X1对Y影响更大。

4.3 回归模型B模型诊断

      首先对自变量进行共线性诊断，结果如表4-3所示。X1和X3的VIF值均小于4，即变量之间不存在多重共线性。

表 4-3  共线性检验

	VIF
X1	1.023639
X3	1.023639

      其次，对模型的正态性、方差齐性与异常值进行诊断，结果如表4-1所示。由QQ图可以得出，残差项基本服从正态分布；由左下角图形可以得出，方差基本保持水平，即满足等方差性；由右下角图形可以得出，大部分点的cook距离均小于0.5，只有第17个点的cook距离>0.5，位于1.0-1.5之间，可以考虑剔除此点，以优化模型。

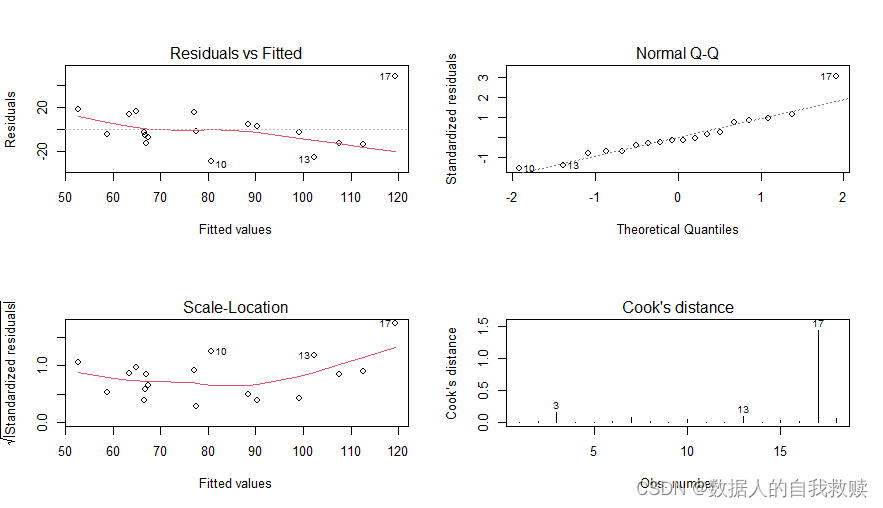
图 4-1  回归模型B诊断

4.4 回归模型C

      考虑到自变量X1对Y影响较大，本文又根据变量X1增设变量X4，具体操作是以X1中位数为分界点将X1数据分为两类，若>X1中位数，则X4=1，否则X4=0，即变量X4为0-1变量。将变量X4那个模型，建立回归模型C。模型结果如表4-4所示。

表4-4  回归模型C结果

	Estimate	Std.Error	t value	Pr(>|t|)
(Intercept)	39.069	17.687	2.209	0.04574*
X1	2.850	0.904	3.153	0.00763**
X2	-0.088	0.405	-0.218	0.83048
X3	0.200	0.111	1.802	0.09475
X4	-25.363	17.609	-1.44	0.17342
R-squared	0.6113
Adjusted R-squared	0.4918
p-value	0.01069

由表4-4可以得出：模型P值为0.01<0.05，即在显著性水平α=0.05 下，模型C具有统计学意义；自变量X1-X4中，只有变量X1通过了检验，即对因变量Y存在显著性影响，X2-X3未通过检验。下面考虑对变量X1-X4进行选择，即建立逐步回归模型，模型结果如表4-5所示。

表4-5  逐步回归模型结果

	Estimate	Std.Error	t value	Pr(>|t|)
(Intercept)	41.479	13.883	2.988	0.009**
X1	1.737	0.467	3.721	0.002**
X3	0.155	0.104	1.494	0.156
R-squared	0.5481
Adjusted R-squared	0.4878
p-value	0.002589

  由表4-5可以得出，经过逐步回归分析，剔除了变量X2和X4，保留了X1和X3，模型结果与回归模型B结果相同，模型解读与诊断与模型B相同。

五、结论及建议

5.1 结论

      通过建立多个回归模型，得出如下结论：土壤内可给态林浓度主要与土壤内无机磷浓度、土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷有关，且前者对可给态磷浓度影响较大。逐步回归模型满足正态性与方差齐性，且通过了显著性检验。根据变量X1增加的0-1变量X4对土壤内可给态磷浓度不存在显著性影响。

5.2 建议

      土壤内所含可给态磷浓度与土壤内无机磷浓度、土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷浓度存在线性回归关系。可以根据土壤内两者浓度，预测土壤内可给态磷浓度，进而预测玉米体内可供态磷浓度的状态与生长态势，指导玉米生产；另一方面，可以通过改善土壤内所含可给态磷浓度，改善玉米的土壤条件，进而提高玉米产量。

六、代码

a=read.csv("D:/个人成长/学业/课程/大三下课程/统计模型/作业/第二次作业/k2co3.csv",header=1)
a[c(1:5),]N = sapply(a,length)
MU = sapply(a,mean)
SD = sapply(a,sd)
MIN = sapply(a,min)
MED = sapply(a,median)
MAX = sapply(a,max)
result = cbind(N,MU,SD,MIN,MED,MAX)
resultpar(mfrow = c(2,2))
hist(a$X1, xlab = "无机磷", ylab = "频数",main=NULL)
hist(a$X2, xlab = "双溶有机磷", ylab = "频数",main=NULL)
hist(a$X3, xlab = "单溶有机磷", ylab = "频数",main=NULL)
hist(a$Y, xlab = "可给太磷", ylab = "频数",main=NULL)
vif(Model.AIC)
library(corrplot)
k=cor(a,use='everything',method='pearson')
par(mfrow=c(1,1))
corrplot(k,addCoef.col = "black")fit = lm(Y~X1+X2+X3, data = a)
summary(fit)Model.AIC=step(fit,trace=F)
summary(Model.AIC)#共线性检验
library(car)
vif(Model.AIC)#模型诊断
par(mfrow = c(2,2))
plot(Model.AIC,which=1)
plot(Model.AIC,which = 2)
plot(Model.AIC,which = 3)
plot(Model.AIC,which = 4)b=read.csv("D:/个人成长/学业/课程/大三下课程/统计模型/作业/第二次作业/k2c032.csv",header=1)fit2 = lm(Y~X1+X2+X3+X4, data = b)
summary(fit2)Model.AIC2=step(fit,trace=F)
summary(Model.AIC2)

---

个人见解，欢迎大家批评指正