To_Heart—总结——FWT(快速沃尔什变换)
目录
- 闲话
- 拿来求什么
- 或
- 与
- 异或
闲话
这个比FFT简单了很多呢,,大概是我可以学懂的水平!
好像是叫 快速沃尔什变换 ?
拿来求什么
以 FFT 来类比。我们 FFT 可以在 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 的复杂度下实现求解:
Ck=∑i+j=kAi×BjC_k=\sum_{i + j=k} A_i \times B_j Ck=i+j=k∑Ai×Bj
那么 FWT 的作用就是再 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 的时间复杂度下面求解:
Ck=∑i⊕j=kAi×BjC_k=\sum_{i \oplus j=k} A_i \times B_j Ck=i⊕j=k∑Ai×Bj
其中的 ⊕\oplus⊕ 是位运算异或的意思。 FWT 应该是支持 ⊕\oplus⊕、∣|∣、 &\&& 三种位运算的。
然后就准备开始讲这三种位运算分别对应的算法。
或
我们定义 FWT(A)i=∑j∣i=iAj\mathrm{FWT(A)_i}=\sum_{j|i=i} A_jFWT(A)i=∑j∣i=iAj。根据定义可以知道 FWT(A)\mathrm{FWT(A)}FWT(A) 是一个由 AAA 构造出来的多项式。先不管如何构造,我们考虑 FWT(A)\mathrm{FWT(A)}FWT(A) 有什么用。我们发现:
FWT(A)×FWT(B)\mathrm{FWT(A)} \times \mathrm{FWT(B)}FWT(A)×FWT(B)
=∑i=0FWT(A)i×FWT(B)i=\sum_{i=0} \mathrm{FWT(A)_i} \times \mathrm{FWT(B)_i}=i=0∑FWT(A)i×FWT(B)i
=∑i=0(∑j∣i=iAj×∑k∣i=iBk)=\sum_{i=0} ( \sum_{j|i=i} A_j \times \sum_{k|i=i} B_ k)=i=0∑(j∣i=i∑Aj×k∣i=i∑Bk)
=∑i=0∑(j∣k)∣i=iAj×Bk=\sum_{i=0} \sum_{(j|k)|i=i} A_j \times B_ k=i=0∑(j∣k)∣i=i∑Aj×Bk
=∑i=0∑(j∣k)∣i=iCi=\sum_{i=0} \sum_{(j|k)|i=i} C_i=i=0∑(j∣k)∣i=i∑Ci
=FWT(C)=\mathrm{FWT(C)}=FWT(C)
所以我们发现可以在 O(n)\mathrm{O(n)}O(n) 的时间复杂度下实现由 A,BA,BA,B 到 CCC 的转换。所以现在的问题就是如何在 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 及以下的时间复杂度中求出 FWT(A)\mathrm{FWT(A)}FWT(A) 。
考虑分治。假设 AAA 有 2n2^n2n 项,那么 A0A_0A0 表示 AAA 的前 2n−12^{n-1}2n−1 ,A1A_1A1 表示 AAA 的后 2n−12^{n-1}2n−1 项。
然后就可以得到一个崭新的转移:
FWT(A)={FWT(A0),FWT(A1)+FWT(A0)n≥1An=0\mathrm{FWT(A)}=\begin{cases}{\mathrm{FWT(A_0)},\mathrm{FWT(A_1)}+\mathrm{FWT(A_0)}}&{n\geq 1}\\{A}&{n=0}\end{cases}FWT(A)={FWT(A0),FWT(A1)+FWT(A0)An≥1n=0
这个 ,可以理解成把两个多项式拼起来。
如何理解这个式子呢?n=0n=0n=0 的边界很好理解,问题在上面一个式子。
你考虑 A0A_0A0 和 A1A_1A1 的区别:在 AAA 中且在 A0A_0A0中 的项的下标的最高位一定是 0 ;在 AAA 中且在 A1A_1A1中 的项的下标的最高位一定是 1 ;
所以你发现从 A0A_0A0 和 A1A_1A1 向 AAA 中只有可能是 A0A_0A0 所在的项给 A1A_1A1 所在的项做贡献。
所以就可以做到 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 的时间复杂度实现从 AAA 到 FWT(A)\mathrm{FWT(A)}FWT(A) 的转换了。
但是还需要实现从 FWT(A)\mathrm{FWT(A)}FWT(A) 到 AAA 的转换,也就是逆转换。
你感性理解一下,大概就是 A_0 会影响的两个位置,其中一个只有 A_0 ,另一个是 A_0+A_1 ,所以设 x_0 为改变的第一个位置, x_1 为改变的第二个位置,那么有 x=A0x=A_0x=A0 和 y=A0+A1y=A_0+A_1y=A0+A1 。现在是知道了 x 和 y ,所以 A0=xA_0=xA0=x,A1=y−A0=y−xA_1=y-A_0=y-xA1=y−A0=y−x
那么关于 或运算 的 FWT 就可以实现了:
void OR(ll *a,int n,int op){ //op=1是顺转换,op=-1是逆转换for(int mid=1;mid<n;mid<<=1) for(int len=mid<<1,j=0;j<n;j+=len) for(int i=j;i<j+mid;i++)a[i+mid]=(a[i+mid]+a[i]*op+Mod)%Mod;
}
与
这个和 或 差不多,但是注意到只有 A1A_1A1 可以向 A0A_0A0 贡献,所以反过来。
void AND(ll *a,int n,int op){for(int mid=1;mid<n;mid<<=1) for(int len=mid<<1,j=0;j<n;j+=len) for(int i=j;i<j+mid;i++)a[i]=(a[i]+a[i+mid]*op+Mod)%Mod;
}
异或
这个可能要麻烦一点。
异或本身并不好统一的下标之间的关联。什么意思呢?对于 或 ,我们可以很清楚的发现对于所有情况都是 A0A_0A0 向 A1A_1A1 做贡献;对于 与,所有情况都是 A1A_1A1 向 A0A_0A0 做贡献。但是异或并不满足这样的性质。所以需要考虑一种构造 FWT\mathrm{FWT}FWT 的方式使得 A0A_0A0 和 A1A_1A1 的做贡献方式是一成不变的。
那么考虑怎么找到构造方式。
相关文章:
)
To_Heart—总结——FWT(快速沃尔什变换)
目录闲话拿来求什么或与异或闲话 这个比FFT简单了很多呢,,大概是我可以学懂的水平! 好像是叫 快速沃尔什变换 ? 拿来求什么 以 FFT 来类比。我们 FFT 可以在 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 的复杂度下实现求解࿱…...

Google巨大漏洞让Win10、11翻车,小姐姐马赛克白打了
早年间电脑截图这项技能未被大多数人掌握时,许多人应该都使用过手机拍屏幕这个原始的方式。 但由于较低的画面质量极其影响其他用户的观感,常常受到大家的调侃。 但到了 Win10、11 ,预装的截图工具让门槛大幅降低。 WinShiftS 就能快速打开…...
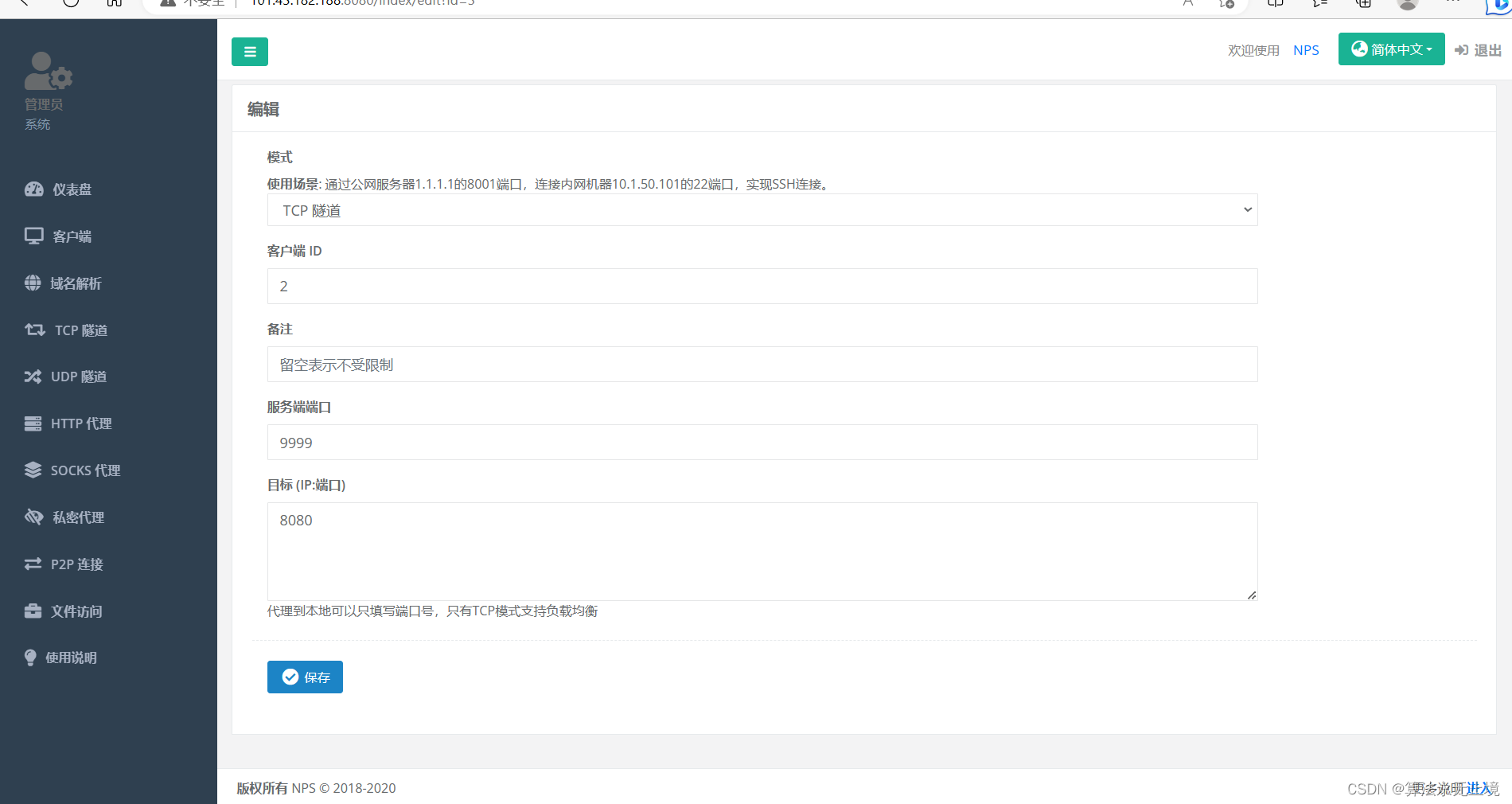
腾讯云服务器部署内网穿透(让其他人在不同ip可以访问我们localhost端口的主机项目)(nps开源项目)
首先打开shell连接我们的云服务器 然后我们再opt目录下面创建一个文件夹用来存放我们的压缩包和文件 mkdir /opt/nps 这个是它官方的安装图解.所以我们按照这个docker安装过程来: 然后我们用docker安装镜像.这样的话比较简单一点 docker pull ffdfgdfg/nps 然后我们查看docker…...

IDS、恶意软件、免杀技术、反病毒技术、APT、对称加密、非对称加密以及SSL的工作过程的技术介绍
IDS的简单介绍IDS是:入侵检测系统(intrusion detection system,简称“IDS”)是一种对网络传输进行即时监视,在发现可疑传输时发出警报或者采取主动反应措施的网络安全设备。它与其他网络安全设备的不同之处便在于&…...
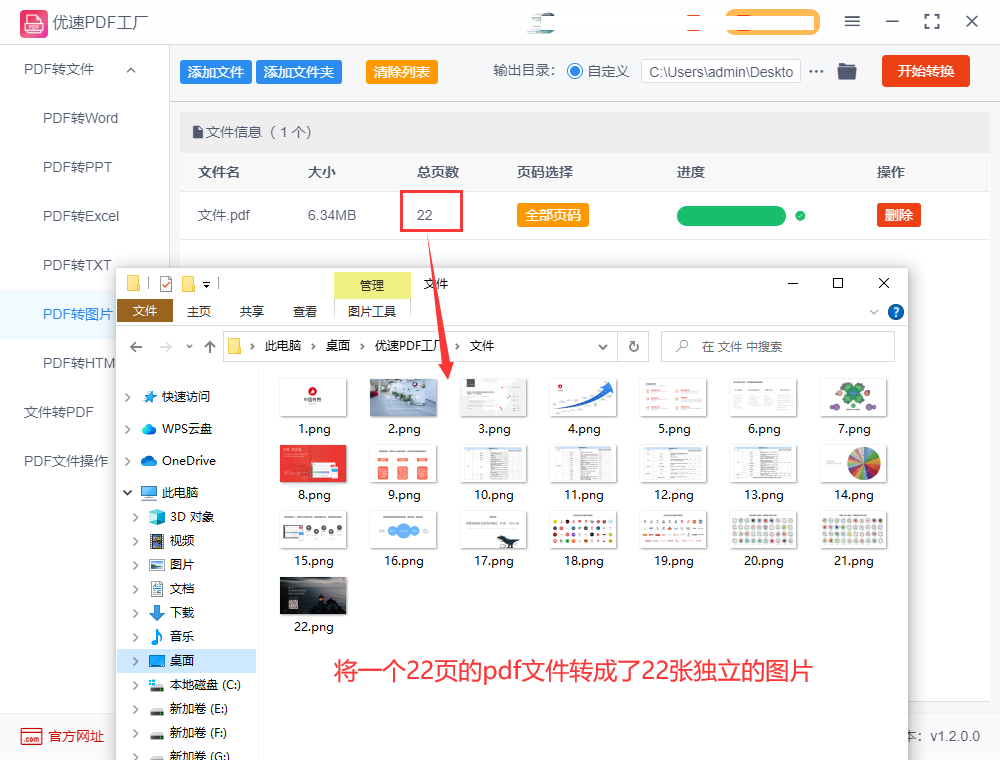
怎么把pdf转换成高清图片
怎么把pdf转换成高清图片?可以使用以下两种方法: 方法一:使用Adobe Acrobat Pro DC 1、打开需要转换的PDF文件,点击“文件”菜单中的“导出为”,在弹出的菜单中选择“图像”,然后选择“JPEG”。 2、在“…...
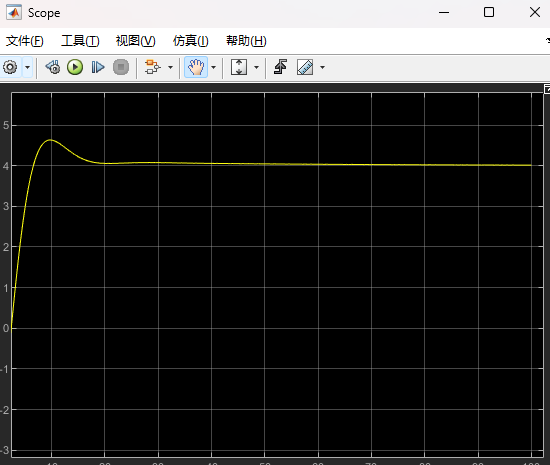
MATLAB 系统辨识 + PID 自动调参
系统辨识 PID 自动调参 文章目录系统辨识 PID 自动调参1. 导入数据1.1 从 Excel 中导入数据2. 系统辨识3. PID 自动调参1. 导入数据 1.1 从 Excel 中导入数据 如果不是从Excel中导入可以跳过该步骤 导入函数: [num,txt,raw]xlsread(xxx\xxx.xlsx);num返回的是…...

【vue3】组合式API之setup()介绍与reactive()函数的使用·上
>😉博主:初映CY的前说(前端领域) ,📒本文核心:setup()概念、 reactive()的使用 【前言】vue3作为vue2的升级版,有着很多的新特性,其中就包括了组合式API,也就是是 Composition API。学习组合…...

爬虫Day3 csv和bs4
爬虫Day3 csv和bs4 一、CSV的读和写 1. 什么是csv文件 csv文件叫做:逗号分隔值文件,像Excel文件一样以行列的形式保存数据,保存数据的时候同一行的多列数据用逗号隔开。 2. csv文件的读写操作 1) csv文件读操作 from csv import reader…...
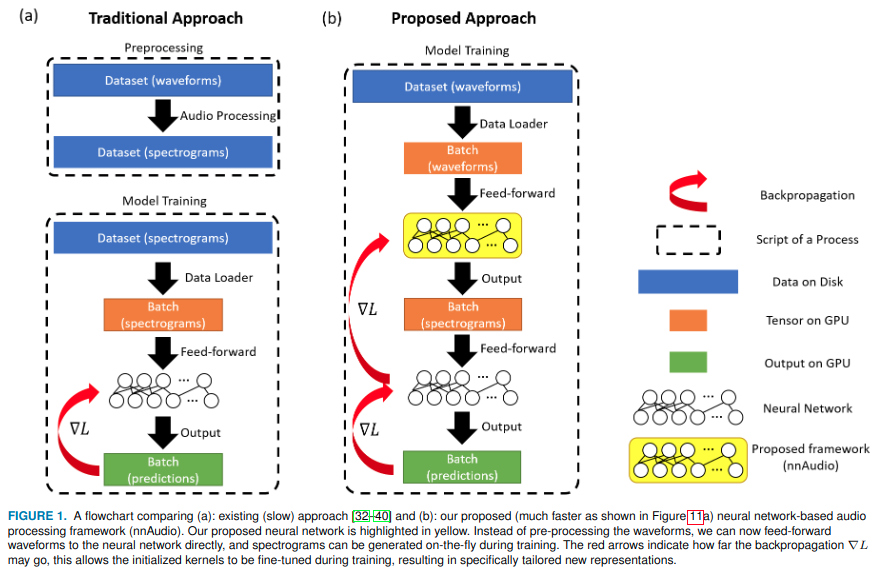
nnAudio的简单介绍
官方实现 https://github.com/KinWaiCheuk/nnAudio; 论文实现: nnAudio: An on-the-Fly GPU Audio to Spectrogram Conversion Toolbox Using 1D Convolutional Neural Networks; 以下先对文章解读: abstract 在本文中&#x…...
)
【id:134】【20分】B. 求最大值最小值(引用)
题目描述 编写函数void find(int *num,int n,int &minIndex,int &maxIndex),求数组num(元素为num[0],num[1],...,num[n-1])中取最小值、最大值的元素下标minIndex,maxIndex(若有相同最值࿰…...

Java 面向对象
一、Java 8 增强的包装类 Java是面向对象的编程语言,但它也包含了8种基本数据类型,这8种基本数据类型不支持面向对象的编程机制,基本数据类型的数据也不具备对象的特性。(没有成员变量、方法可以被调用)。Java之所以提…...
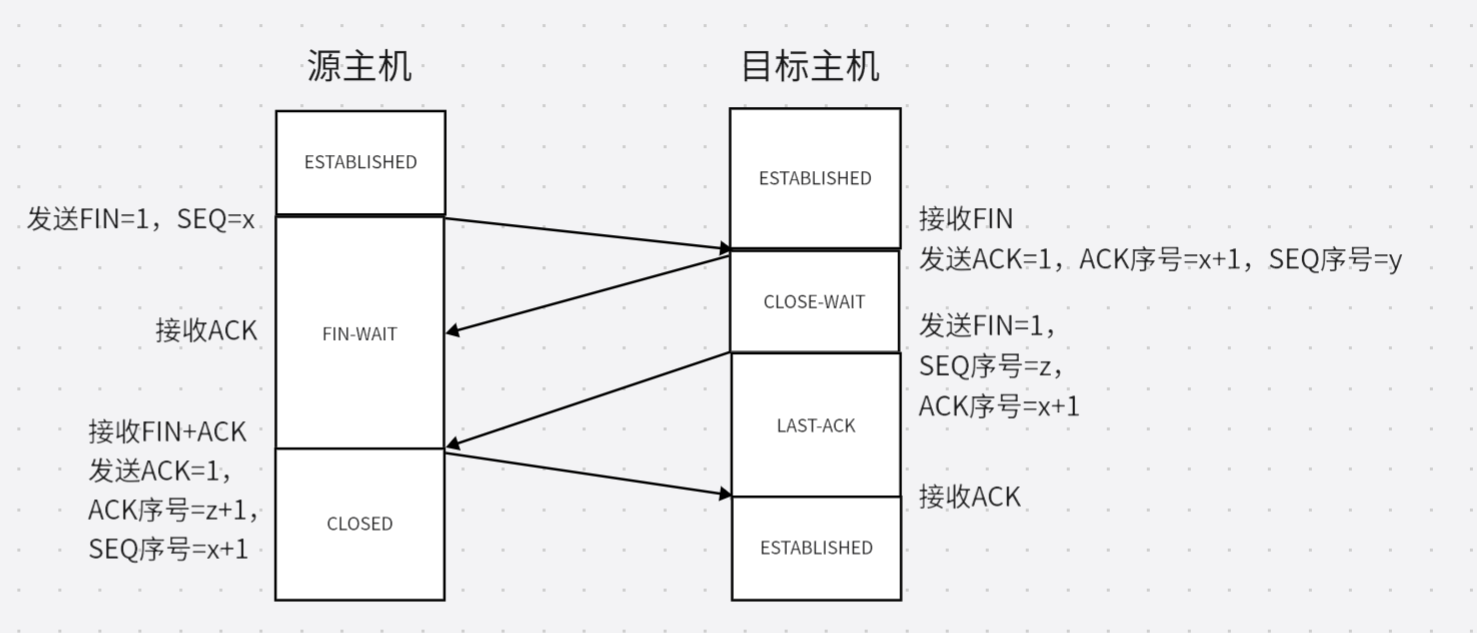
五、传输层
(一)TCP传输控制协议 可靠的、面向连接的字节流服务,全双工,有端口寻址功能 1、TCP的三种机制 1.使用序号对分段的数据进行标记,便于调整数据包 2.TCP使用确认、校验和和定时器系统提供可靠性 3.TCP使用可变大小的…...

Thinkphp 6.0一对一关联查询
本节课我们来了解关联模型中,一对一关联查询的使用方法。 一.hasOne 模式 1. hasOne 模式,适合主表关联附表,具体设置方式如下: hasOne(关联模型,[外键,主键]); return $this->hasOne(Profile::class,user_id, id); 关联模型&…...
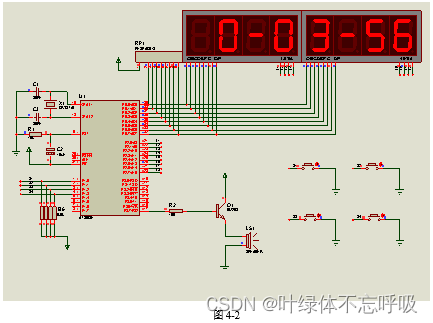
基于51单片机的自动打铃打鸣作息报时系统AT89C51数码管三极管时钟电路
wx供重浩:创享日记 对话框发送:单片机打铃 获取完整无水印论文报告说明(含源码程序、电路原理图和仿真图) 本次设计中的LED数码管电子时钟电路采用24小时制记时方式,本次设计采用AT89C51单片机的扩展芯片和6个PNP三极管做驱动&…...

算法详解-双指针算法的魅力-一种简单而高效的编程思想
文章目录双指针简介快慢指针快慢指针介绍快慢指针例题快慢指针优缺点:对撞指针对撞指针介绍:对撞指针例题对撞指针优缺点:更新中——未完总结更多宝藏双指针简介 😎🥳😎🤠😮&#x…...

网页审查元素
在讲解爬虫内容之前,我们需要先学习一项写爬虫的必备技能:审查元素(如果已掌握,可跳过此部分内容)。1、审查元素在浏览器的地址栏输入URL地址,在网页处右键单击,找到检查。(不同浏览器的叫法不同…...

gpt2 adapter finetune
1. 安装依赖: pip install -U adapter-transformers pip install datasets 2.训练代码: from datasets import load_dataset from transformers import AutoModelForCausalLM from transformers import GPT2Tokenizer from transformers import Adap…...

Day14_文件操作
一、数据存储 1.1 计算机数据存储 计算机内存分为运行内存和硬盘两种:保存在运行内存中的数据在程序运行结束后会自动释放,保存在硬盘中的数据会一直存在(除非手动删除或者硬盘损坏) 1)打开文件 open(文件路径, 文件打开方式‘r’, encod…...

leetcode 轮转数组 189
题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,1,2…...

Leetcode.1849 将字符串拆分为递减的连续值
题目链接 Leetcode.1849 将字符串拆分为递减的连续值 Rating : 1747 题目描述 给你一个仅由数字组成的字符串 s。 请你判断能否将 s拆分成 两个或者多个 非空子字符串 ,使子字符串的 数值 按 降序 排列,且每两个 相邻子字符串 的数值之 差 …...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
