2/12考试总结
时间安排
8:30–8:50 读题,T1 不知道是个啥,T2是个dp ,T3可能也是 dp 之类的。
8:50–9:30 T1,读了好几遍才理解了题意,对于部分分有爆搜。考虑正解,想到预处理后O(1) 查询,问题是如何由已知的信息得到所有可能询问的答案,想了几种 子集dp 之类的东西,都不太对。
9:30–10:20 T2,看了一眼发现有 70 分是送的。正解貌似可以前缀和优化一下什么的。仔细分析了一下发现不好维护,暴力前缀和预处理的话时间空间都不允许,尝试着化简式子看看能不能 O(1) 做,貌似做不了。
10:20–11:13 T3,分析题目可以找到一些性质,然后根据这个建图,部分分可以暴力在图上跑。考虑能不能推广,需要快速知道图上的信息,猜了好几个结论都是假的。
11:13–12:00 瞪T1,T3。
12:00–13:00 瞪T1 。
回顾反思
T1:
正解是 dfs 搜索,或者使用状压做类似过程,复杂度是 n2nn2^nn2n 的。
比赛时一开始读题理解题意耽误了一点时间。
题目中有 ∃∀\exist \forall∃∀ 两种逻辑运算,将 ∃\exist∃ 当做限制,问题是如何预处理出一个限制是否被满足。考场上,我局限于先以某种方式钦定一个限制,然后考虑在限制下的所有可能状态的解,那么这样复杂度就是枚举限制的复杂度与枚举状态复杂度的积,是不能通过的。但是实际上,根本不需要事先钦定某个限制,可以直接将限制的钦定融进状态的枚举中,考虑直接一位一位枚举状态,对于某一位,讨论是采取限制 1 还是限制 2 ,然后得到在此限制下下一位的合法状态,递归进入下一位。这样,递归进入某一位是,之前的所有位的信息都能被有效利用,而非再次搜索产生冗余。
这道题,我在最开始题意的理解上出现了一些偏差,绕了一些弯子;其次,我局限于钦定限制然后找状态,但是实际上可以枚举状态然后讨论限制,边枚举边做;再者,我对 dfs 的复杂度没有信心,没有仔细去计算 dfs的实际复杂度。
要认真分析复杂度,一般的 dfs 会有很多不必要的冗余,若能够做到最大化利用每一段递归公共的部分减少重复冗余操作,其复杂度会极大的降低。
T2:
思路基本和正解相同,考虑组产生的分界,但是角度又略有不同。正解主要考虑是 A 组先满还是 B 组先满,而我则是考虑在给定的 K 的关键点内 B 组是否满了。这两种角度对于部分分计算的复杂度是一样的,但是我涉及的组合数整体的分布不如正解的 “亲近” ,比较难以优化计算;其次,正解的式子几乎只涉及了值域为 n 的 i 以及种数为 n\sqrt nn 的 K,那么枚举 K 对 i 暴力预处理就行了,而我还涉及到另一个值域为 n 的变量 xk ,于是预处理也很困难。于是进行不下去了。
还是要尝试多种角度的思考问题,不仅是这种思路能走多远的问题,更直接的,不同的角度会对式子产生不同的影响。
对于具体的计算方法,
对于每个询问涉及到某种分布或者某段的组合数的计算,直接计算或者预处理都不好做,可以考虑优化暴力,将询问对应的区间离线下来,对相应数值跑莫队,这样可以做到根号。
对于正解,其计算难点在于出现了以 k 为参数的式子,这个 k 值域是 1->n ,若对于每个 1-> n 都预处理是不现实的。但是注意题目条件 ∑k≤2∗n\sum k\leq 2*n∑k≤2∗n ,那么不同的 k 的种数最多只有 n\sqrt nn 级别,于是将 k 离线下来只对这根号个 k 预处理就可以了。
很多题目都涉及了对 ∑k≤lim\sum k\leq lim∑k≤lim 这个条件性质的利用,如该题中 k 种类数不超过根号、虚树等。
T3:
想到建图了,建了图,但是对于图的性质没有剖析完全,模型中出现了许多冗余边。具体的,正解的建图是若干条链,相邻的链连边,而我对于一条链与许多不相邻的链也连了边,但实际上这些边即使不加,也存在相应的等价的路径。于是我的图模型不像题解那样简洁,比较乱,也没有规律可循。
这种建模题,连边时要谨慎,考虑到这条边是否有加的必要,是否不需要这条边也能表现出相应的等价关系,精简模型,透露本质。
题目有充要性质:相同的 ai 对应的 pi 递减,且对于一个 pi 大于 i 之前最近的一个满足 aj=ai-1 的 pj 。由此建图,是若干条相连的链。
这个图比较简单,信息可以直接递推处理。
三道题都没有涉及什么比较复杂的算法和数据结构,T1是暴力题,T2是经典套路题,T3难度也不算很高,其实都在个人可控范围内,T1,T2都是应该 AC 的题目,理想分数应该在 250+ 以上。
相关文章:

2/12考试总结
时间安排 8:30–8:50 读题,T1 不知道是个啥,T2是个dp ,T3可能也是 dp 之类的。 8:50–9:30 T1,读了好几遍才理解了题意,对于部分分有爆搜。考虑正解,想到预处理后O(1) 查询,问题是如何由已知的信息得到所有…...
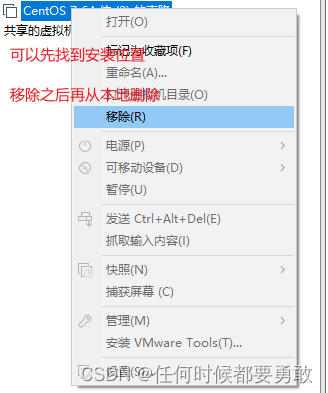
第三章虚拟机的克隆,快照,迁移删除
1.虚拟机的克隆 如果你已经安装了一台linux操作系统,你还想再更多的,没有必要再重新安装,你只需要克 隆就可以,看演示。 方式1,直接拷贝一份安装好的虚拟机文件,再用虚拟机打开这个文件方式2,使用vmware的…...
| 真题含思路)
华为OD机试 - 任务总执行时长(Python)| 真题含思路
任务总执行时长 题目 任务编排服务负责对任务进行组合调度。 参与编排的任务又两种类型, 其中一种执行时长为taskA, 另一种执行时长为taskB。 任务一旦开始执行不能被打断,且任务可连续执行。 服务每次可以编排 num 个任务。 请编写一个方法,生成每次编排后的任务所有可…...
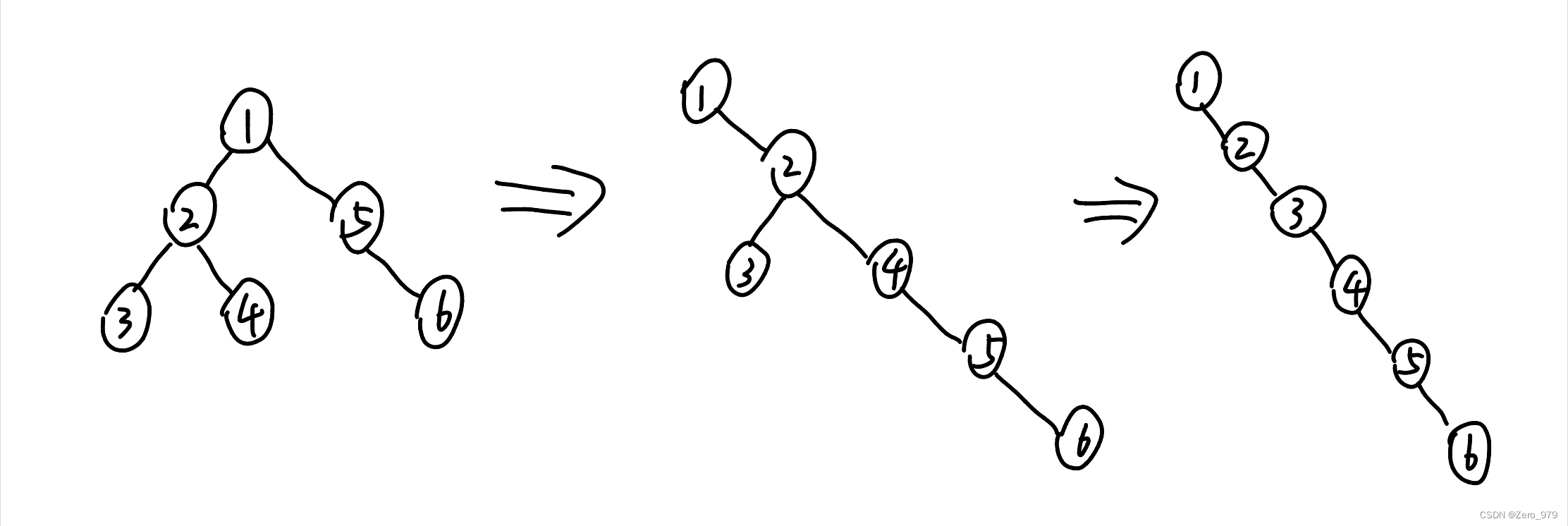
LeetCode 热题 C++ 114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。展开后的单链表应该与二叉树 先序遍历 顺序相同。 示例 1…...

Spring的事务控制-基于AOP的声明式事务控制
Spring的事务控制-基于AOP的声明式事务控制 Spring事务编程概述 事务是开发中必不可少的东西,使用JDBC开发时,我们使用connection对事务进行控制,使用MyBatis时,我们使用SqlSession对事务进行控制,缺点就是ÿ…...
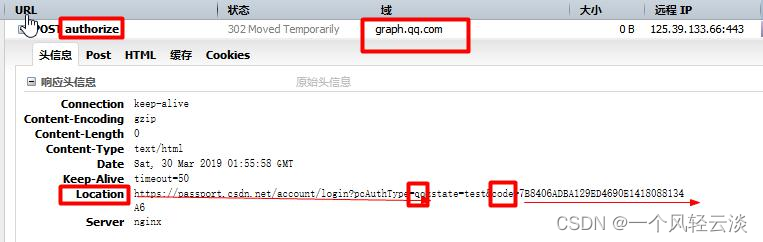
SSO(单点登陆)
Single Sign On 一处登陆、处处可用 0、前置概念: 1)、单点登录业务介绍 早期单一服务器,用户认证。 缺点:单点性能压力,无法扩展 分布式, SSO(single sign on)模式 解决 : 用户身份信息独…...
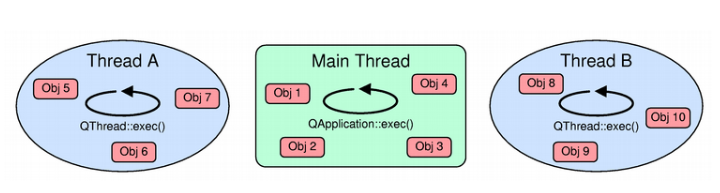
线程和QObjects
QObject的可重入性: QThread继承了QObject,它发出信号以指示线程开始或完成执行,并提供一些插槽。 QObjects可以在多个线程中使用发出调用其他线程中槽的信号,并将事件发布到在其他线程中“活动”的对象。这是可能的࿰…...

最新中文版FL Studio21水果软件下载安装图文教程
FL Studio是目前流行广泛使用人数最多音乐编曲制作软件,这款软件相信广大网友并不陌生,今天带来的是FL中文版本,所有的功能都能在线编辑,用户直接就能操作,同时因为是21水果是最新版,所以增加了新的功能&am…...

pandas数据分析35——多个数据框实现笛卡尔积
什么是笛卡尔积。就是遍历所有组合的可能性。 比如第一个盒子有[1,2,3]三个号码球,第二个盒子有[4,5]两个号码球。那么从每个盒子里面分别拿一个球共有3*2两种可能性,其集合就是{[1,4],[2,4],[3,4],[1,5],[2,5],[3,5]},这个就是笛卡尔积。 三个盒子也是…...

【C语言学习笔记】:数组倒序排列,数组倒置
数组倒置就是将数组元素中的数据倒过来! 举个例子,比如下面程序: #include <stdio.h>int main(void) { int a[5] {1, 2, 3, 4, 5}; int b[5]; //用来存放倒置后的数据 int i, j; for (i0, j4; i<5, j>0; i, --j)…...
sni+tomcat漏洞复现
sni SNI产生背景 SSL以及TLS(SSL的升级版)为客户端与服务器端进行安全连接提供了条件。但是,由于当时技术限制,SSL初期的设计顺应经典的公钥基础设施 PKI(Public Key Infrastructure)设计,PKI 认为一个服务器只为一个…...
Linux ALSA 之十:ALSA ASOC Machine Driver
ALSA ASOC Machine Driver一、Machine 简介二、ASoC Machine Driver2.1 Machine Driver 的 Platform Driver & Platform Device 驱动模型2.2 在 Probe() 中注册声卡三、snd_soc_register_card 函数3.1 bind DAIs3.2 New a sound card3.3 Create card new widgets3.4 Probe …...

Spring 面试题(一):Spring 如何处理全局异常?
❤️ 博客首页:水滴技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 🌸 订阅专栏:Spring 教程:从入门到精通 文章目录1、如何处理全局异常2、代码示例2.1、定义统一的“响应结果对象”2.2、…...
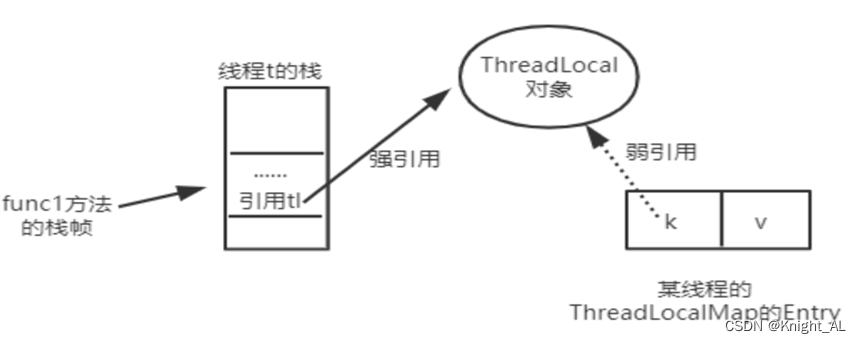
Threadlocal为何引发内存泄漏问题
首先我们要先了解什么是泄漏问题和什么是内存溢出 内存泄漏表示程序员申请了内存,但是该内存一直无法被释放 内存溢出表示申请内存不足,就会报错 为何引发内存泄漏问题 因为每个线程都有自己独立的ThreadLocalMap对象,key为ThreadLocal&…...

如何写好 Python 的 Lambda 函数?
当你需要完成一件小工作时,在本地环境中使用这个函数,可以让工作如此得心应手,它就是 Lambda 函数。 Lambda 函数是 Python 中的匿名函数。有些人将它们简称为lambdas,它们的语法如下: lambda arguments: expression…...

大数据技术架构(组件)32——Spark:Spark SQL--Execute Engine
2.2、Spark SQL2.2.1、Execute EngineSparkSql的整体提交执行流程和Hive的执行流程基本上一致。站在通用的角度,对于SparkSql来说,从Sql到Spark的RDD执行需要经历两个大的阶段:逻辑计划和物理计划逻辑计划层面会把用户提交的sql转换成树型结构…...
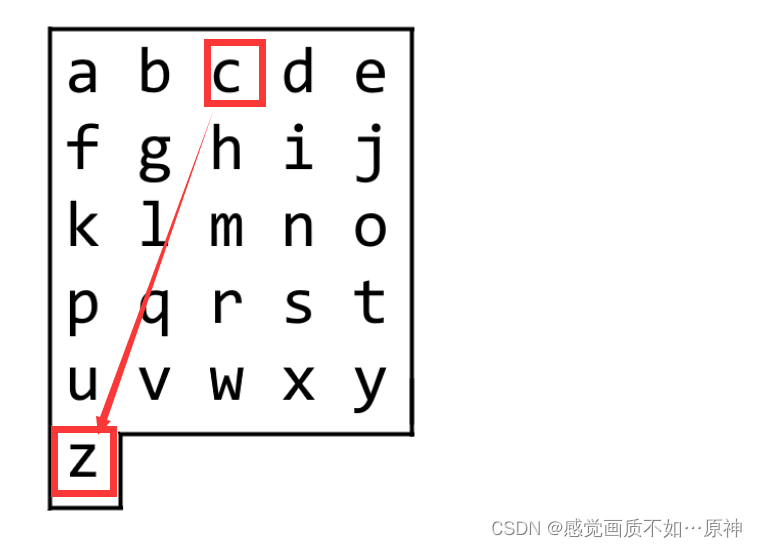
Leetcode.1138 字母板上的路径
题目链接 Leetcode.1138 字母板上的路径 Rating : 1411 题目描述 我们从一块字母板上的位置 (0, 0)出发,该坐标对应的字符为 board[0][0]。 在本题里,字母板为board ["abcde", "fghij", "klmno", "pqr…...

一个自动配置 opengrok 多项目的脚本
前段时间在服务器上配置 opengrok 阅读代码,项目有很多个,一个一个手动配置比较繁琐。 我从搭建 tomcat 和 opengrok,到配置和索引完 5 个 Android 项目,用了差不多一整天。 要是再让我手动配置几个项目,估计真要崩溃…...

JAVA同步代码块 同步方法
JAVA同步代码块 & 同步方法 为了解决多线程操作共享数据时产生的安全问题 例如以下代码 if (ticket < 0) {// 卖完了break; } else {ticket--;System.out.println(Thread.currentThread().getName() "在卖票,还剩下" ticket "张")…...

分享111个助理类简历模板,总有一款适合您
分享111个助理类简历模板,总有一款适合您 111个助理类简历模板下载链接:https://pan.baidu.com/s/1JafYuLPQMmq37K4V0wiqWA?pwd8y54 提取码:8y54 Python采集代码下载链接:https://wwgn.lanzoul.com/iKGwb0kye3wj 设计师助理…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
