神经网络损失函数分布可视化神器
论文名称和地址:
Visualizing the Loss Landscape of Neural Nets
https://arxiv.org/pdf/1712.09913.pdf
1.1 背景和动机
作者主要想研究几个问题:
为什么我们能够最小化高度非凸神经损失函数?
为什么得到的最小值这个结果具有泛化性?
不同的神经网络网络架构如何影响损失函数分布 (loss landascape),以及训练的超参数参数如何影响损失函数分布
1.2 损失函数可视化基础
一般通过最小化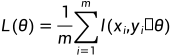 来训练神经网络。其中,
来训练神经网络。其中, 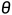 表示神经网络的参数, 函数
表示神经网络的参数, 函数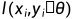 衡量神经网络对数据样本标签的预测程度, m 为数据样本的个数。神经网络包含许多参数, 因此它们的损失函数存在于一个非常高维的空间中。
衡量神经网络对数据样本标签的预测程度, m 为数据样本的个数。神经网络包含许多参数, 因此它们的损失函数存在于一个非常高维的空间中。
一维的线性插值可视化方法
一种已有的1维的可视化方法是线性插值法 (Linear interpolation), 就是选择两个参数向量  和
和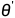 , 并沿连接这两点的直线
, 并沿连接这两点的直线 绘制损失函数的值
绘制损失函数的值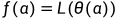 。
。
但是一维线性插值方法有几个缺点。
一维线性插值方法去可视化神经网络的非凸性 (non-convexities) 是很困难的,这就导致了损失函数在最小化轨迹上似乎缺乏局部最小值。
一些损失函数具有非凸性,而这些非凸性与不同网络架构之间的泛化差异相关。
一维线性插值方法不考虑 Batch Normalization 或者网络中的不变性对称性。因此,由一维线性插值方法产生的插值结果可能具有误导性。
二维的线性插值可视化方法
为了使用二维的线性插值可视化方法, 我们可以在图中选择首先一个中心点 , 并选择两个方向向量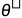
 和
和 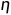 。
。
然后, 在 1D (曲线) 情况下, 绘制一个形式为 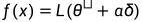 的函数, 或者在 2D (平面) 情况下, 绘制一个形式为
的函数, 或者在 2D (平面) 情况下, 绘制一个形式为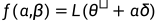 的函数。
的函数。
以上方法的问题
虽然以上这两种在随机方向移动一个小距离,并绘制函数值的绘图方法很简单,但它无法捕捉损失函数的固有几何形状,并且不能用于比较两个不同的最小化器或两个不同的神经网络模型的几何形状。这是因为网络权重的比例不变性 (scale invariance) 。当使用 ReLU 非线性激活函数时,如果将网络中某一层的权重乘以10,并将下一层的权重除以10,网络输出将保持不变。当使用 BN 时,同理也存在这种不变性。
那么网络权重的比例不变性 (scale invariance) 对于以上的一维,二维的线性插值可视化方法有哪些影响呢?
——具有较大权重的神经网络可能具有平滑且缓慢变化的损失函数:比如说,如果权重的幅值比1大得多,那么将权重扰动一个单位对网络性能的影响很小。但是如果权重远小于1,那么同样的单位扰动可能会产生很大的影响,使损失函数对权重扰动显得相当敏感。
1.3 Filter Normalization
基于以上一维和二维的线性插值可视化方法的缺点,本文提出一种叫做 Filter Normalization 的可视化方法。这种方法的思想也是基于以上的一维,二维的线性插值可视化方法。
以上方法问题的核心其实就来自于 "单位扰动" ,即:
对于权重幅值较大的神经网络而言,一个单位的扰动对它没啥作用,即使得 loss 的改变几乎可以忽略不计,那么它就更可能具有一个平滑且缓慢变化的 loss landscape。
对于权重幅值较小的神经网络而言,一个单位的扰动对它会产生很大的影响,使得 loss 发生灾难性的改变,使得 loss landscape 对权重扰动显得相当敏感。
那么为了克服这个难题, 本文作者提出一种滤波器归一化 (Filter Normalization) 的做法, 即:对于网络权重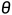 , 和一个随机的高斯方向向量d , 然后作者将d 中的每个滤波器归一化, 使其具有与
, 和一个随机的高斯方向向量d , 然后作者将d 中的每个滤波器归一化, 使其具有与 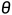 中相应滤波器相同的范数。换句话说, 进行替换, 如下式所示:
中相应滤波器相同的范数。换句话说, 进行替换, 如下式所示:
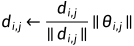
式中, d_{i,j} 代表第i 层, 第j 个滤波器的高斯方向向量, 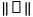 代表 Frobenius 范数。滤波器归一 化 (Filter Normalization) 并不局限于卷积 (Conv) 层, 也适用于全连接(FC) 层 (相当于
代表 Frobenius 范数。滤波器归一 化 (Filter Normalization) 并不局限于卷积 (Conv) 层, 也适用于全连接(FC) 层 (相当于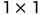 卷 积)。
卷 积)。
作者在下一节证明了经过滤波器归一化的图的锐度与泛化误差有很好的相关性,而没有滤波器归一化的图可能非常具有误导性。
1.4 可视化实验
Loss landscape 尖锐,扁平的困境
在上一节中,我们提到有的神经网络具有平滑且缓慢变化的 loss landscape (称为 sharp minimizer),而有的具有剧烈变化的 loss landscape (称为 flat minimizer)。在本节中,将通过一些实验结果阐明:sharp minimizer 和 flat minimizer 的泛化性有什么关系?
在这里呢,作者探讨了 sharp minimizer 和 flat minimizer 的区别。
作者表明:使用传统的一维线性插值方法得到的结论是:sharp minimizer 和 flat minimizer 的泛化性没什么关系
曲线的锐度与模型的泛化性之间很好地相关。大 Batch Size 产生视觉上更尖锐的最小值 (尽管不是很明显),但测试误差更高。

不同 Batch Size 使用滤波器归一化 1D 和 2D 的可视化结果
1.5 一些 Loss Surfaces 非凸结构的发现
大量经验表明,似乎有些神经结构比其他的更容易最小化。例如,使用 Skip Connection,ResNet 使得我们可以训练非常深的神经网络结构,而没有 Skip Connection 的相同的神经网络结构是不可训练的。而且,一个网络是否可以得到良好的训练很大程度上取决于训练开始时的初始参数。
作者使用可视化方法,对神经结构进行了实证研究,以探索为什么损失函数的非凸性在某些情况下似乎是有问题的
模型深度的影响
如下图所示,可以看到,当不使用残差连接时,网络深度对神经网络的 loss landscape 有显著的影响。比如当深度为20时,不使用残差连接的 ResNet-20-NS 有较好的表现,这并不太令人惊讶,因为用于 ImageNet 的原始VGG 网络有19层,也可以有效地训练。但是,随着网络深度的增加,VGG 类网络的损失面自发地从 (近) 凸过渡到混沌。ResNet-56-NS 具有显著的非凸性和大区域,其中梯度方向 (与图中描绘的等高线正常) 不指向中心的最小值。而且,随着向某些方向移动,损失函数会变得非常大。ResNet-110-NS 显示出更明显的非凸性,当我们在图中所示的各个方向移动时,它变得非常陡峭。
图中的对比很强烈——当神经网络比较浅时,不使用快捷连接(shortcut connection)对于损失分布的影响还不算大,即上图中的(a)和(d)图。
当网络达到了 56 层的深度时,无快捷连接(shortcut connection)的模型的等高线图中显示的损失函数基本是混乱的(图(e))。特别是在一些区域中,沿着梯度的方向运动并不能达到损失更小的区域。
这显然是很危险的,意味着梯度下降方法的效率被大大损害了;同时也从另一方面解释了模型的训练性,即为何有些模型的训练更容易,或者对于同一模型为何超参数的取值不同会对模型表现造成巨大影响。
假如模型初始化后落入了一个高度非凸的区域中,在整个训练过程中算法可能都无法找到一个比较好的解,因为梯度所指向的方向根本毫无意义。上图第三栏中,ResNet-110-noshort 显示了更极端的非凸性,不管向哪一个方向移动梯度都非常大。
我们特别需要注意的是在上图第一行中——即有快捷连接(shortcut connection)的 ResNet——即使模型的深度大大增加,中心的极小值的深度也并没有增加多少,即模型收敛的区域仍然是相对平坦的。而第二行中当我们去掉了 ResNet 的快捷连接(shortcut connection)时,图像中心紫线所代表的极小值的深度大大增加了。这样一个最直接的影响——上文已经提到——就是训练难度增加了。
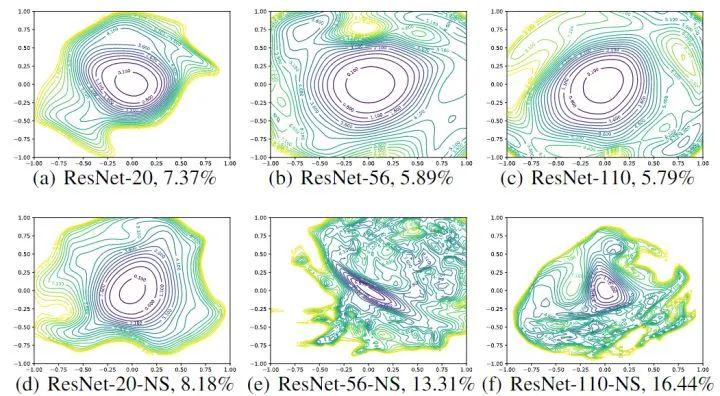
图3:Wide-ResNet-56 有残差连接 (上) 和无残差连接 (下) 的 loss landscape,k=2 意思是每层滤波器数量乘以2
有无残差连接的影响
残差连接对损失函数的 loss landscape 有显著的影响。在上图3中可以看到,随着深度的增加,残差连接阻止了向混沌行为的过渡。残差连接的影响似乎对深的网络架构最为重要。对于更浅的网络 (ResNet-20 和 ResNet-20-NS),残差连接的影响不明显。如下图4所示是 ResNet-56 有无残差连接的 loss landscape 对比,图5所示是 ResNet-110 无残差连接和 DenseNet 121 层的 loss landscape 对比。
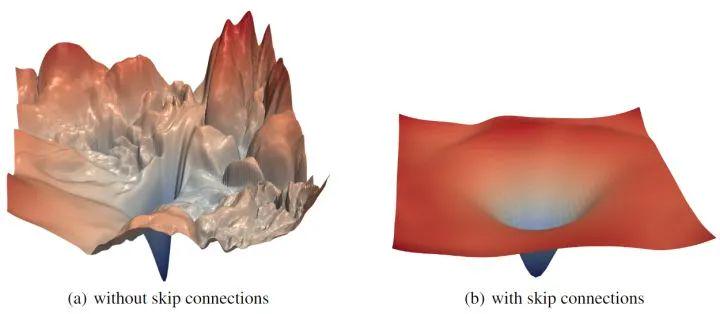
图4:ResNet-56 有无残差连接的 loss landscape 对比
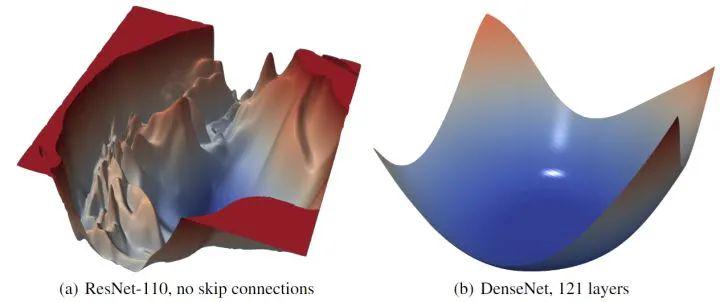
图5:ResNet-110 无残差连接和 DenseNet 121 层的 loss landscape 对比
模型宽度的影响
另一个比较有意思的发现在于,当神经网络的宽度增加——即每层的神经元个数增加——损失函数的曲面也变得更平滑了。这里作者使用了 RestNet 56 层的结构,仍然是第一行有快捷连接(shortcut connection),第二行无。其中每个子图下面的 k 表示隐藏神经元的倍数,即 k=2 为模型的宽度是 k=1 的模型的二倍。旁边的百分比数字表示模型的错误率。
可以看到更宽的模型的 loss landscape 更宽,即:增大网络宽度可以获得更宽更平坦的 loss landscape。
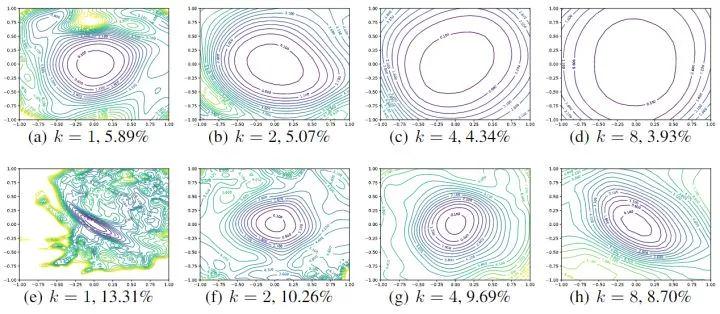
图6. Wide-ResNet-56 有残差连接 (上) 和无残差连接 (下) 的 loss landscape,k=2 意思是每层滤波器数量乘以2
[图片来源:Hao, L. et al. (2018). Visualizing the loss landscape of neural nets. NIPS.]
我们首先从上到下两两对比地讨论这些结果,可以看到有快捷连接(shortcut connection)总是比无快捷连接(shortcut connection)的损失函数曲面更平滑一些,极小值的位置也更浅。不过更重要的是当我们从左到右的进行分析时——随着模型宽度的增加,模型的损失曲面显著地变得更平缓了,也就是更浅了。
对于没有快捷连接(shortcut connection)的模型来说,增加模型宽度也许不能直接解决损失函数的分布中存在梯度混乱的问题,图(f)的四角都可以看到有很不平滑的等高线,但由于曲面变得更浅,我们可以侧面缓解这个问题。
网络初始化的影响
在图3中看到的一个有趣的性质是,网络的 loss landscape 似乎都可以分成两种区域:一种是损失函数值相对较低,loss landscape 的凸性很好;一种是损失函数值相对较高,loss landscape 的凸性很差。这种混沌和凸区域的划分可能解释了良好初始化策略的重要性。
如果一个神经网络模型的 loss landscape 很平坦,那么初始化的位置很可能位于具有 "良好表现" 的损失函数区域,可能永远不会出于非凸的部分。相反,如果一个神经网络模型的 loss landscape 很陡峭,那么初始化的位置很可能由于梯度不足导致增加优化的难度。
图3和图6都表明,loss landscape 对泛化性有显著的影响。混沌,陡峭的 loss landscape (没有残差连接的深度网络) 导致更糟糕的训练和测试误差,而更凸的景观具有更低的误差值。
总结
本文提出一种基于 "Filter Normalization" 的简单可视化方法。当使用这种归一化时,最小化的锐度与泛化误差有很高的相关性,这种展示的可视化结果非常清晰。
本文观察到,当网络变得足够深时,神经网络的 loss landscape 会迅速从接近凸的状态过渡到高度混乱的状态。这种从凸到混沌行为的转变伴随着泛化误差的急剧下降,并最终导致整个网络可训练性的下降。
本文观察到,残差连接促进了 loss landscape 更加平坦,并阻止了向混沌行为的过渡,这有助于解释为什么残差连接对于训练极深的网络是必要的。
本文通过计算在局部极小值附近 Hessian 矩阵的的最小 (最负) 特征值来定量测量非凸性,并将结果可视化为 heatmap。
本文研究了 SGD 优化轨迹的可视化,也解释了可视化这些轨迹时出现的困难。
相关文章:

神经网络损失函数分布可视化神器
论文名称和地址:Visualizing the Loss Landscape of Neural Netshttps://arxiv.org/pdf/1712.09913.pdf1.1 背景和动机作者主要想研究几个问题:为什么我们能够最小化高度非凸神经损失函数?为什么得到的最小值这个结果具有泛化性?不…...
ansible的部署与命令模块
目录 一、ansible的概述 1、ansible简介 2、ansible特点 3、官方网站 4、ansible的模块组成 5、ansible的工作机制 二、ansible部署 1、ansible的安装 三、ansible的命令行模块 1、command模块 2、shell模块 3、cron模块 4、user模块 5、group模块 6、copy模块 7…...
开发人员与测试人员关系的理解
在软件开发中都会有开发人员(以下简称开发)和测试人员(以下简称测试),在一些小型公司可能并没有测试,仅仅是开发兼任测试。在这里我仅针对于有专业的测试和专业的开发的项目。 每个公司应该都有考核机制&am…...
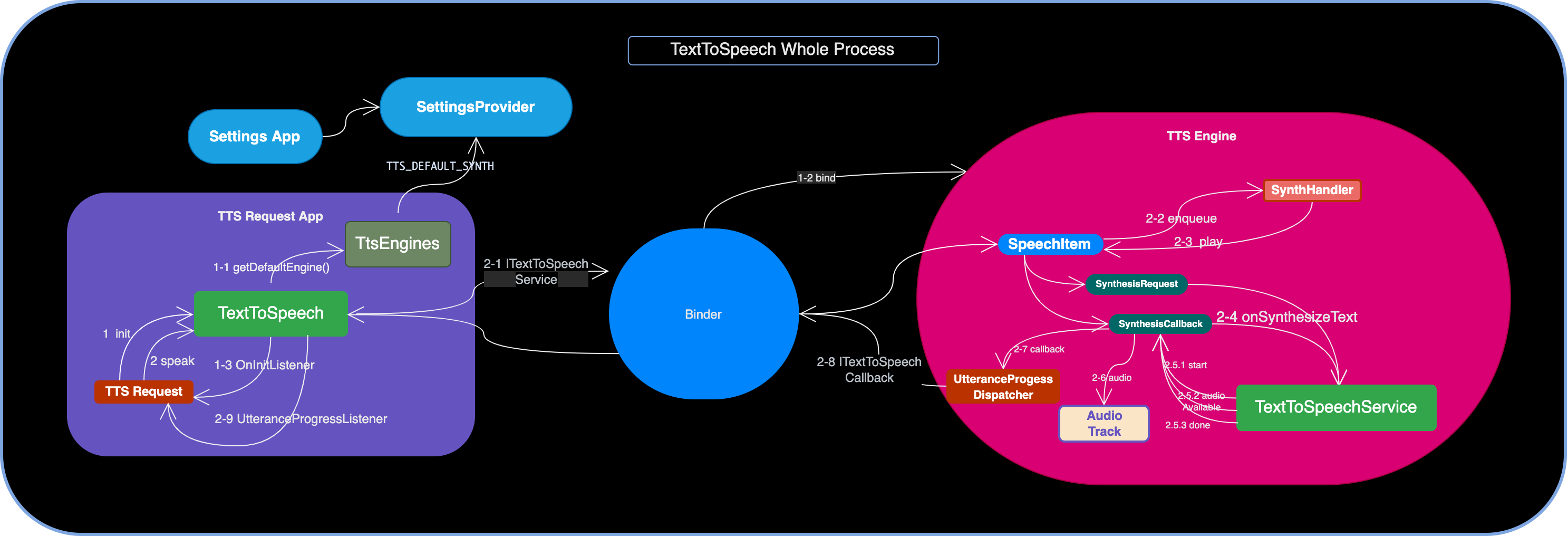
直面原理:5 张图彻底了解 Android TextToSpeech 机制
ChatGPT 如此火爆,但它的强悍在于 NLU(自然语言理解)、DM(对话管理)和 NLG (自然语言生成)这三块,而 Recognition 识别和 TTS 播报这两块是缺失的。假使你的 App 接入了 ChatGPT&…...

Ruby Socket 编程
Ruby提供了两个级别访问网络的服务,在底层你可以访问操作系统,它可以让你实现客户端和服务器为面向连接和无连接协议的基本套接字支持。 Ruby 统一支持应用程序的网络协议,如FTP、HTTP等。 不管是高层的还是底层的。ruby提供了一些基本类&a…...

Vue3+ElementPlus+koa2实现本地图片的上传
一、示例图二、实现过程利用Koa2书写提交图片的后台接口这个模块是我写的项目中的其中一个板块——上传图片,这个项目的后台接口主要是是使用了后端的Koa2框架,前端小伙伴想要试着自己书写一些增删改查的接口可以从这个入手,Koa2用来了解后端…...
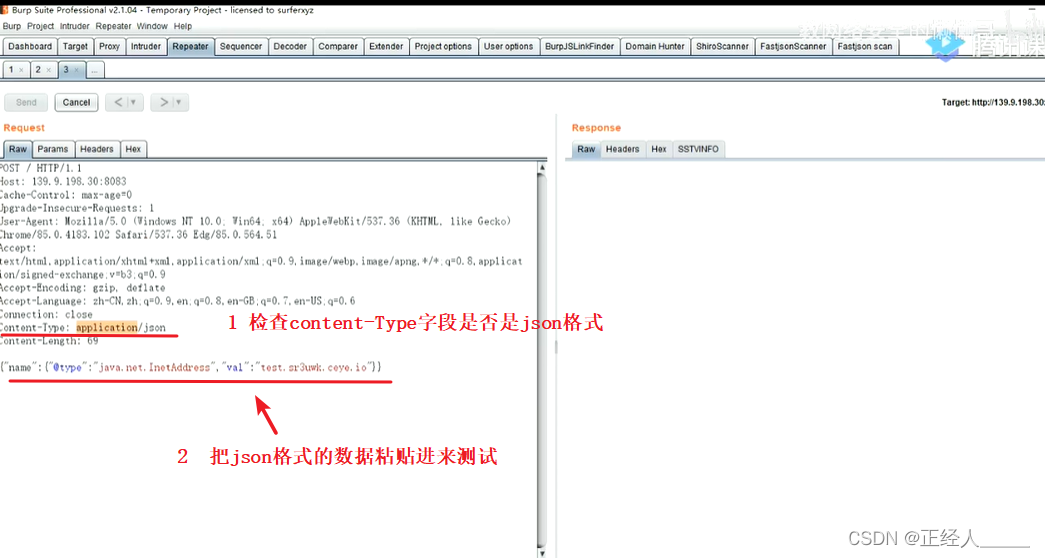
常见漏洞之 Fastjson
数据来源 01 Fastjson相关介绍 》Fastjson概述 》Fastjson历史漏洞 02 Fastson的识别与漏洞发现 》Fastjson寻找 》Fastjson漏洞发现(利用 dnslog) 03 修复建议 建议1:使用fastjson1.2.83版本; Github地址:https:…...
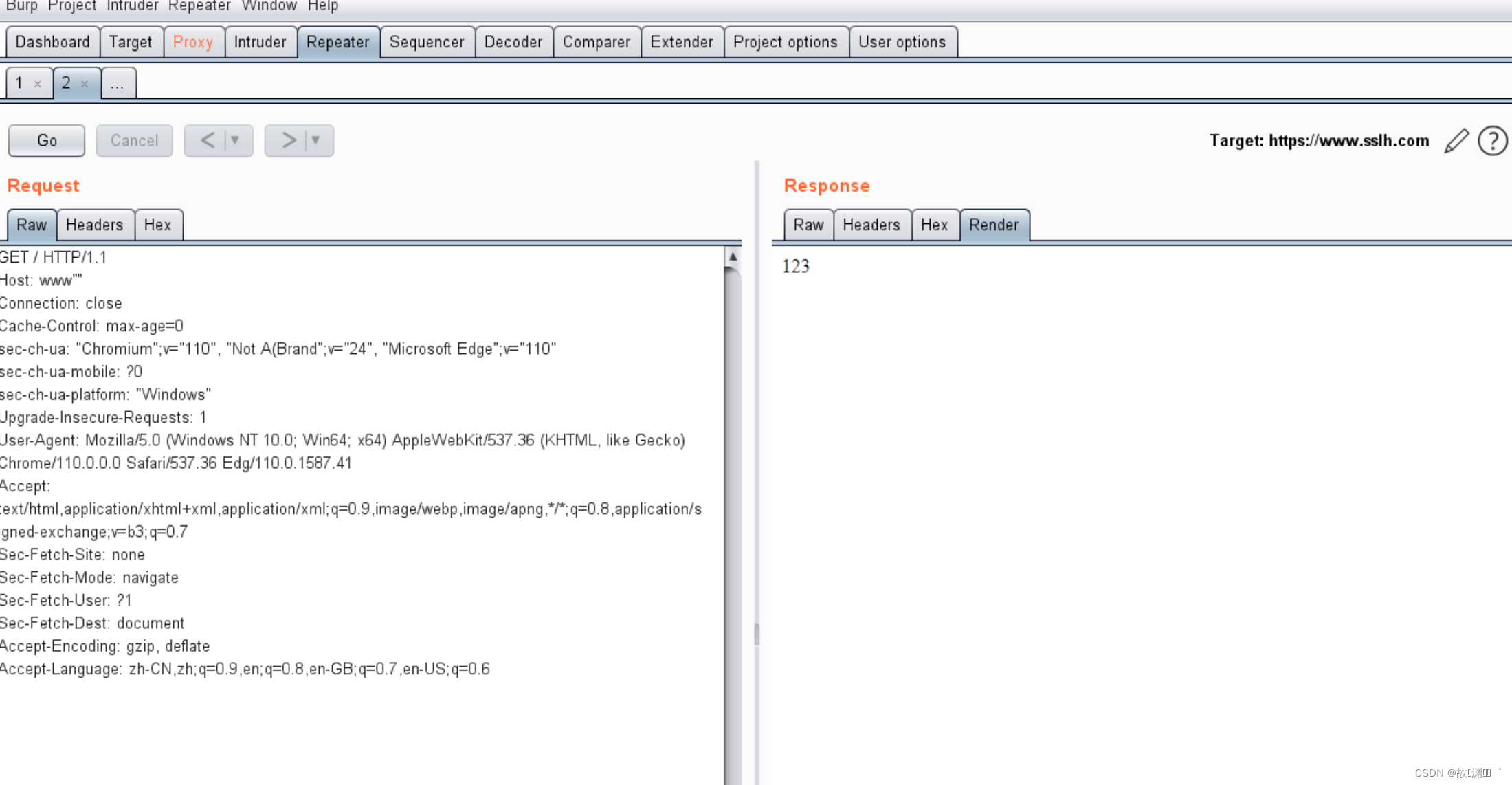
绕过Nginx Host限制
目录绕过Nginx Host限制SNI第三种方法:总结绕过Nginx Host限制 SNI SNI(Server Name Indication)是 TLS 的扩展,这允许在握手过程开始时通过客户端告诉它正在连接的服务器的主机名称。 作用:用来解决一个服务器拥有…...

Visual Studio 2022 常用快捷键,记录一下别忘记~
Visual Studio 2022 常用快捷键,记录一下别忘记~ CtrlEC 注释代码 CtrlEU 取消注释代码 CtrlED 格式化全部代码 CtrlShiftA 新建类 CtrlRG 删除无效Using CtrlH 批量替换 CtrlG 跳转到指定行 CtrlEE 在交互窗口中运行选中代码(很实用) AltEnter 快速引用 …...

软件测试回顾---重点知识
软件测试重点知识回顾 8.1.1软件测试的目的是 尽可能的发现程序中的错误并不是发现所有的错误并不是证明程序是错误的也不是为了调试程序8.1.2白盒测试根据什么设置测试用例?黑盒测试根据什么设置测试用例? 白盒测试根据内部逻辑来设计的黑盒测试根据的是…...

2D图像处理:2D Shape_Base_Matching_缩放_旋转_ICP_显示ROI
文章目录 调试结果参考调试说明问题0:并行运行问题问题1:模板+Mask大小问题问题2:组合缩放和旋转问题3:可以直接将计算边缘的代码删除问题4:如何在原始图像上显示匹配到的ROI问题5:计算的原始旋转角度不需要判断,直接可以在ICP中使用问题6:绘制坐标轴问题7:绘制ROI调试…...
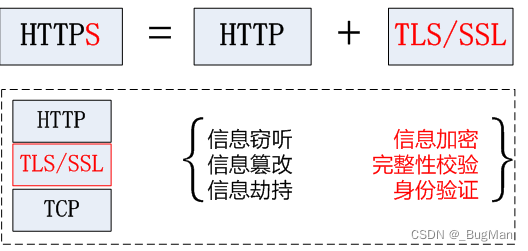
HTTP、HTTPS
目录 1.HTTP 1.1.概述 1.2.报文结构 1.2.1.请求报文 1.2.2.响应报文 1.3.方法 2.HTTPS 1.HTTP 1.1.概述 HTTP,超文本传输协议,WEB体系选用了该协议作为应用层协议。 1.2.报文结构 1.2.1.请求报文 HTTP的请求报文(request࿰…...

计算机网络之http03:HTTPS RSA握手解析
不同的秘钥交换算法,握手过程可能略有差别 上文对HTTPS四次握手的学习 SSL/TLS Secure Sockets Layer/Transport Layer Security 协议握手过程 四次通信:请求服务端公钥 2次 秘钥协商 2次 (1)ClientHello请求 客户端向服务端发送client…...
一款针对EF Core轻量级分表分库、读写分离的开源项目
更多开源项目请查看:一个专注推荐.Net开源项目的榜单 在项目开发中,如果数据量比较大,比如日志记录,我们往往会采用分表分库的方案;为了提升性能,把数据库查询与更新操作分开,这时候就要采用读写…...
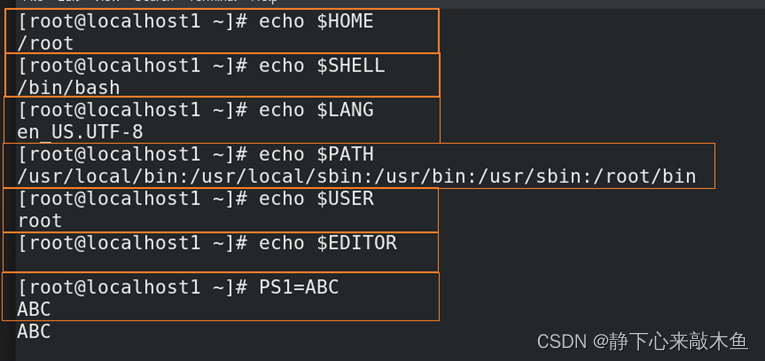
Linux环境变量讲解
目录 环境变量 alias命令 type命令 变量分类 Linux最主要的全局环境变量 环境变量 变量是计算机系统用于保存可变数值的数据类型 在Linux中,一般变量都是大写,命令是小写 在Linux中,变量直接使用,不需要定义(更快…...

iptables和nftables的使用
文章目录前言iptable简介iptable命令使用iptables的四表五链nftables简介nftables命令的时候nftables与iptables的区别iptables-legacy和iptables-nft实例将指定protocol:ip:port的流量转发到本地指定端口前言 本文展示了,iptables和nftable命令的使用。 # 实验环…...
中小学信息学相关编程比赛清单及报名网站汇总(C++类)
1、NOI系列比赛(CSP-J CSP-S NOIP NOI APIO CTSC IOI ISIJ等) NOI官网 NOI全国青少年信息学奥林匹克竞赛https://www.noi.cn/ 2、蓝桥杯青少年创意编程大赛 https://www.lanqiaoqingshao.cn/home 3、中国电子协会考评中心...

06Makefile
Makefile 1、Makefile简介 一个工程中的源文件不计其数,其按类型、功能、模块分别放在若干个目录中,makefile定义了一系列的规则来指定哪些文件需要先编译,哪些文件需要后编译,哪些文件需要重新编译,甚至于进行更复杂…...

【C++】模板初阶
🍅讨厌废话,直接上车 ☃️1.泛型编程 void Swap(int& left, int& right) { int temp left; left right; right temp; } void Swap(double& left, double& right) { double temp left; left right; right temp; } void Swap(char&…...
vue+nodejs考研资料分享系统vscode - Visual Studio Code
前端技术:nodejsvueelementui,视图层其实质就是vue页面,通过编写vue页面从而展示在浏览器中,编写完成的vue页面要能够和控制器类进行交互,从而使得用户在点击网页进行操作时能够正常。 Express 框架于Node运行环境的Web框架, 目 …...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
