基于skopt的贝叶斯优化基础实例学习实践
贝叶斯方法是非常基础且重要的方法,在前文中断断续续也有所介绍,感兴趣的话可以自行移步阅读即可:
《数学之美番外篇:平凡而又神奇的贝叶斯方法》
《贝叶斯深度学习——基于PyMC3的变分推理》
《模型优化调参利器贝叶斯优化bayesian-optimization实践》
在《模型优化调参利器贝叶斯优化bayesian-optimization实践》 一文中,我们基于bayesian-optimization库来实现了贝叶斯优化实践,本文同样是要应用实践贝叶斯优化方法,只不过这里我们使用的是skopt模块来完成对应的实践的。
对于目标函数f:
noise_level = 0.1def f(x, noise_level=noise_level):return np.sin(5 * x[0]) * (1 - np.tanh(x[0] ** 2))\+ np.random.randn() * noise_level可以先绘制f的边界轮廓,如下;
x = np.linspace(-2, 2, 400).reshape(-1, 1)
fx = [f(x_i, noise_level=0.0) for x_i in x]
plt.plot(x, fx, "r--", label="True (unknown)")
plt.fill(np.concatenate([x, x[::-1]]),np.concatenate(([fx_i - 1.9600 * noise_level for fx_i in fx],[fx_i + 1.9600 * noise_level for fx_i in fx[::-1]])),alpha=.45, fc="g", ec="None")
plt.legend()
plt.title("Function Contours")
plt.show()结果如下所示:

贝叶斯优化是建立在高斯过程之上的,如果每个函数评估都很昂贵,例如,当参数是神经网络的超参数且函数评估是十倍的平均交叉验证分数时,则使用标准优化例程优化超参数将永远花费!
其思想是使用高斯过程来近似函数。换句话说,假定函数值遵循多元高斯分布。函数值的协方差由参数之间的GP核给出。然后,利用捕获函数在高斯先验下选择下一个待评估参数,使得评估速度更快。
from skopt import gp_minimizeres = gp_minimize(f, # the function to minimize[(-2.0, 2.0)], # the bounds on each dimension of xacq_func="EI", # the acquisition functionn_calls=15, # the number of evaluations of fn_random_starts=5, # the number of random initialization pointsnoise=0.1**2, # the noise level (optional)random_state=1234) # the random seed计算过程输出如下所示:
fun: -1.0079192525206238func_vals: array([ 0.03716044, 0.00673852, 0.63515442, -0.16042062, 0.10695907,-0.24436726, -0.58630532, 0.05238726, -1.00791925, -0.98466748,-0.86259916, 0.18102445, -0.10782771, 0.00815673, -0.79756401])models: [GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5) + WhiteKernel(noise_level=0.01),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775)]random_state: RandomState(MT19937) at 0x1BC23E3DDB0space: Space([Real(low=-2.0, high=2.0, prior='uniform', transform='normalize')])specs: {'args': {'model_queue_size': None, 'n_jobs': 1, 'kappa': 1.96, 'xi': 0.01, 'n_restarts_optimizer': 5, 'n_points': 10000, 'callback': None, 'verbose': False, 'random_state': RandomState(MT19937) at 0x1BC23E3DDB0, 'y0': None, 'x0': None, 'acq_optimizer': 'auto', 'acq_func': 'EI', 'initial_point_generator': 'random', 'n_initial_points': 10, 'n_random_starts': 5, 'n_calls': 15, 'base_estimator': GaussianProcessRegressor(kernel=1**2 * Matern(length_scale=1, nu=2.5),n_restarts_optimizer=2, noise=0.010000000000000002,normalize_y=True, random_state=822569775), 'dimensions': Space([Real(low=-2.0, high=2.0, prior='uniform', transform='normalize')]), 'func': <function f at 0x000001BBC7401E18>}, 'function': 'base_minimize'}x: [-0.3551841563751006]x_iters: [[-0.009345334109402526], [1.2713537644662787], [0.4484475787090836], [1.0854396754496047], [1.4426790855107496], [0.9579248468740365], [-0.4515808656827538], [-0.6859481043867404], [-0.3551841563751006], [-0.29315378760492994], [-0.3209941584981484], [-2.0], [2.0], [-1.3373741960111043], [-0.24784229191660678]]同样可以对收敛的过程进行可视化:
from skopt.plots import plot_convergence
plot_convergence(res)结果如下所示:

接下来可以进一步检查可视化:1、拟合gp模型到原始函数的近似 2、确定下一个要查询点的采集值
接下来绘制5个随机点下的五个迭代:
def f_wo_noise(x):return f(x, noise_level=0)for n_iter in range(5):# Plot true function.plt.subplot(5, 2, 2*n_iter+1)if n_iter == 0:show_legend = Trueelse:show_legend = Falseax = plot_gaussian_process(res, n_calls=n_iter,objective=f_wo_noise,noise_level=noise_level,show_legend=show_legend, show_title=False,show_next_point=False, show_acq_func=False)ax.set_ylabel("")ax.set_xlabel("")# Plot EI(x)plt.subplot(5, 2, 2*n_iter+2)ax = plot_gaussian_process(res, n_calls=n_iter,show_legend=show_legend, show_title=False,show_mu=False, show_acq_func=True,show_observations=False,show_next_point=True)ax.set_ylabel("")ax.set_xlabel("")plt.show()可视化结果如下所示:

第一列表示:1、真实的的函数、高斯过程模型对原函数的逼近、GP逼近的确定程度。
第二列显示每个代理模型拟合后的采集函数值。我们可能不选择全局最小值,而是根据用于最小化捕获函数的最小值选择局部最小值。在更接近之前在处计算的点处,方差下降为零。最后,随着点数的增加,GP模型更接近实际函数。最后几个点聚集在最小值附近,因为GP无法通过进一步探索获得更多信息:

相关文章:

基于skopt的贝叶斯优化基础实例学习实践
贝叶斯方法是非常基础且重要的方法,在前文中断断续续也有所介绍,感兴趣的话可以自行移步阅读即可: 《数学之美番外篇:平凡而又神奇的贝叶斯方法》 《贝叶斯深度学习——基于PyMC3的变分推理》 《模型优化调参利器贝叶斯优化bay…...

OJ在线评测系统 后端 用策略模式优化判题机架构
判题机架构优化(策略模式) 思考 我们的判题策略可能会有很多种 比如 我们的代码沙箱本身执行程序需要消耗时间 这个时间可能不同的编程语言是不同的 比如沙箱执行Java要额外花费2秒 我们可以采用策略模式 针对不同的情况 定义不同独立的策略 而不是把所有情况全部放在一个i…...

element ui 精确控制日期控件 date-picker
https://github.com/element-plus/element-plus/discussions/17378 -- 某组件 xxx.vue ... <el-date-pickerv-model"timeRange"type"daterange"range-separator"-"start-placeholder"开始日期"end-placeholder"结束日期"…...

centos7安装指定版本php及扩展
安装EPEL仓库(如果尚未安装) sudo yum install epel-release导入REMI仓库的公钥: sudo rpm --import http://rpms.remirepo.net/RPM-GPG-KEY-remi启用REMI仓库(你可以选择PHP 7.0或者7.4,以下以7.0为例)&am…...

后端-对表格数据进行添加、删除和修改
一、添加 要求: 按下添加按钮出现一个板块输入添加的数据信息,点击板块的添加按钮,添加;点击取消,板块消失。 实现: 1.首先,设计页面输入框格式,表格首行 2.从数据库里调数据 3.添加…...
【学习笔记】手写 Tomcat 七
目录 一、优化 Dao 1. 设置 UserDaoImpl 为单例模式 2. 创建 Dao 工厂 3. 在 Service 层获取 UserDao 的实例 二、优化 Service 1. 设置 UserServiceImpl 为单例模式 2. 创建 Service 工厂 3. 在 Servlet 层获取 Service 实现类的对象 三、优化 Servlet 1. 使用配置…...

QT开发:详解 Qt 多线程编程核心类 QThread:基本概念与使用方法
1. 引言 在现代应用程序开发中,多线程编程是一个关键技术,能够显著提高程序的效率和响应速度。Qt 是一个跨平台的 C 框架,其中 QThread 类是实现多线程编程的核心类。本文将深入详解 QThread 的基本概念、使用方法及其在实际应用中的重要性。…...
【芋道源码】gitee很火的开源项目pig——后台管理快速开发框架使用笔记(微服务版之本地开发环境篇)
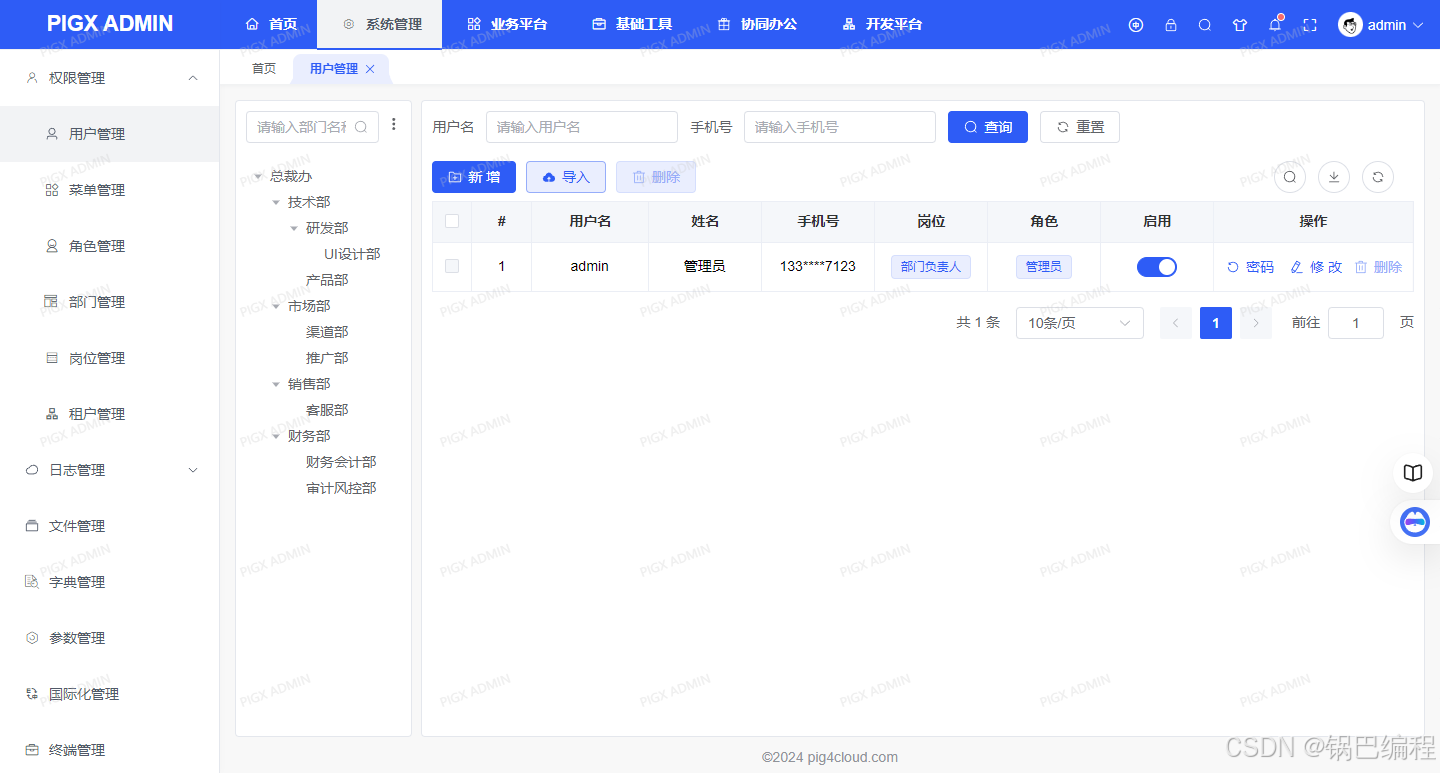
后台管理快速开发框架使用笔记(微服务版之本地开发环境篇) 后台管理快速开发框架使用笔记(微服务版之本地开发环境篇) 后台管理快速开发框架使用笔记(微服务版之本地开发环境篇)前言一、如何获取项目&#…...

设计模式、系统设计 record part01
技术路线: 工程师》设计师》分析师》架构师 管理路线: 项目经理》技术经理 工程师: 编程技术、测试技术 设计师: 工程师设计技术 分析师: 设计师分析技术 架构师: 分析师架构技术 项目经理: 时间…...

服务器与普通电脑的区别是什么?
服务器作为企业进行线上业务所使用的网络设备,大多数的用户对于服务器都有一定的了解,而普通的电脑则是人们在进行日常娱乐活动中经常会用到的设备,本文就来探讨一下服务器与普通电脑之间的区别是什么吧! 普通的电脑就是我们通常所…...

Vue3学习(六)Vue3 + ts几种写法
前言 官网提到组合式api和选项式api 选项式api其实就是vue2的写法,组合式api是vue3的新写法(组合式api可以在script中使用setup()也可以使用<script setup>,<script setup>是setup(ÿ…...

【前端】ES6:Proxy代理和Reflect对象
文章目录 1 Proxy代理1.1 get方法1.2 set方法1.3 has方法1.4 this问题 2 Reflect对象2.1 代替Object的某些方法2.2 修改某些Object方法返回结果2.3 命令式变为函数行为2.4 配合Proxy 1 Proxy代理 Proxy如其名,它的作用是在对象和和对象的属性值之间设置一个代理&am…...

基于微信开发助手企鹅音乐微信小程序的设计与实现(源码+文档+讲解)
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…...

学习Spring Boot,应该从哪里开始学起
文章目录 前言1. Java基础2. Spring框架基础3. Spring Boot入门4. 搭建Spring Boot项目5. 编写RESTful API6. 数据库操作7. 安全性和测试8. 部署和运维9. 实践和项目总结前言 学习Spring Boot,应该从哪里开始学起 学习Spring Boot,你可以从以下几个步骤开始学起: 1. Java基…...

【JavaEE初阶】深入解析死锁的产生和避免以及内存不可见问题
前言: 🌈上期博客:【后端开发】JavaEE初阶—线程安全问题与加锁原理(超详解)-CSDN博客 🔥感兴趣的小伙伴看一看小编主页:GGBondlctrl-CSDN博客 ⭐️小编会在后端开发的学习中不断更新~~~ &#…...

企微群管理软件:构建高效社群运营的新引擎
在数字化营销日益盛行的今天,企业微信(简称“企微”)群作为企业与用户直接互动的重要平台,其管理与运营效率直接关系到企业的品牌形象、用户满意度及市场影响力。企微群管理软件,作为专为企微社群设计的高效管理工具&a…...

CORE 中间件、wwwroot
ASP.NET Core中间件组件是被组装到应用程序管道中以处理HTTP请求和响应的软件组件(从技术上来说,组件只是C#类)。 ASP.NET Core应用程序中的每个中间件组件都执行以下任务。 选择是否将 HTTP 请求传递给管道中的下一个组件。这可…...

SpringBoot 与 Maven 快速上手指南
SpringBoot 与 Maven 快速上手指南 在Java开发领域,Spring Boot和Maven是两个极其重要的工具,它们极大地简化了企业级应用的开发和构建过程。Spring Boot通过自动配置和起步依赖等特性,让开发者能够快速搭建起一个Spring应用;而M…...

大觅网之自动化部署(Automated Deployment of Da Mi Network)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 本人主要分享计算机核心技…...

【C++】入门基础知识-1
🍬个人主页:Yanni.— 🌈数据结构:Data Structure. 🎂C语言笔记:C Language Notes 🏀OJ题分享: Topic Sharing 目录 前言: C关键字 命名空间 命名空间介…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
