【2024.9.28练习】青蛙的约会
题目描述

题目分析
由于两只青蛙都在跳跃导致变量多,不妨采用物理题中的相对运动思想,设青蛙A不动,青蛙B每次跳米,两只青蛙的距离为
米。正常来说,只要模拟青蛙B与青蛙A的相对运动过程,最终当青蛙B与青蛙A距离为0时即可求得总跳跃次数。但是难点在于数据量大,按部就班的模拟将会超时。
由于这是一道有关整数和环的数学题,考虑使用扩展欧几里得算法求解。现直接假设一只青蛙静止,另一只青蛙每次位移为,总跳跃次数为
,一圈长度为
,跳跃的圈数为
,青蛙间的距离为
。则题目满足方程:
。显然要使方程有整数解,必须满足的条件是:
必须是
和
的最大公约数的倍数,即
。这可以通过贝祖定理证明。
接下来的难点是求出最小跳跃次数。根据拓展欧几里得算法已经得到了方程的一组特解,但这不一定是最优解,根据线性同余方程的通解公式:
只需让该特解模除即可求出跳跃次数在
间的最小正整数解。
提交后有一处测试点有误,经检查,原来在exgcd算法中,如果两个参数存在负数,输出的最大公因数也可能是负数。这并不影响所得特解的正确性,但在求最小正解的时候,需要采取措施让取模后的结果转变为正数。
我的代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;// 扩展欧几里得算法
ll extgcd(ll a, ll b, ll& x, ll& y) {if (b == 0) {x = 1;y = 0;return a;}ll d = extgcd(b, a % b, y, x);y -= (a / b) * x;return d;
}int main() {ll x, y, m, n, L;cin >> x >> y >> m >> n >> L;ll a = n - m; // 移项后得到 a = n - mll b = x - y; // 常数项 b = x - yll l = L; // 模数为 Lll x0, y0;ll d = extgcd(a, l, x0, y0); // 使用扩展欧几里得求解if (b % d != 0) {cout << "Impossible" << endl;}else {// 存在解的情况,求最小非负整数解ll k = (x0 * (b / d)) % (l / d); //其中x0*(b/d)为一个方程的特解if (k < 0) {if (l / d > 0) {k += l / d; // 保证 k 为非负}else {k -= l / d; // 保证 k 为非负}}cout << k << endl;}return 0;
}
由于扩展欧几里得算法参数使用了引用,导致逻辑相对更难理解,我利用原本欧几里得算法的数学递推逻辑修改为一下函数,程序可以成功运行:
ll x_0;
ll y_0;
ll x_1;
ll y_1;
ll extgcd(ll a, ll b) {ll d = a;if (b != 0) {d = extgcd(b, a % b);x_0 = y_1;y_0 = x_1 - a / b * y_1;y_1 = y_0;x_1 = x_0;}else {x_1 = 1;y_1 = 0;}return d;
}相关文章:
【2024.9.28练习】青蛙的约会
题目描述 题目分析 由于两只青蛙都在跳跃导致变量多,不妨采用物理题中的相对运动思想,设青蛙A不动,青蛙B每次跳米,两只青蛙的距离为米。正常来说,只要模拟青蛙B与青蛙A的相对运动过程,最终当青蛙B与青蛙A距…...

Python入门:类的异步资源管理与回收( __del__ 方法中如何调用异步函数)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 文章内容 📒📝 使用上下文管理器📝 使用 `__del__` 方法📝 结合使用上下文管理器与 `__del__`📝 资源回收的重要性⚓️ 相关链接 ⚓️📖 介绍 📖 在编程中,资源的管理和回收至关重要,尤其是在处理网络请求时。频…...

Android开发中的ViewModel
在Android应用开发中,ViewModel作为架构组件之一,扮演着管理UI数据和生命周期的关键角色。本文将深入探讨ViewModel如何感知View的生命周期,并分析其内核原理,帮助开发者更好地利用ViewModel优化应用架构。 一、ViewModel简介 在…...

Vue 3 文件编译流程详解与 Babel 的使用
文章目录 一、背景二、结论三、vitejs/plugin-vue 插件调试前物料准备vuePlugin 入口buildStart 方法transform 方法 四、vue/compiler-sfc 核心包parse 方法compileScript、rewriteDefault 方法compileTemplate 方法 五、整体架构六、总结参考资料 一、背景 最近正在研究 rea…...

Android常用C++特性之std::chrono
声明:本文内容生成自ChatGPT,目的是为方便大家了解学习作为引用到作者的其他文章中。 std::chrono 是 C11 引入的标准库中的时间处理工具,提供了以多种精度进行时间测量、处理和操作的功能。它允许开发者处理时间点(time_point&am…...

[Oracle] ORA-04036: 实例使用的 PGA 内存超出 PGA_AGGREGATE_LIMIT
有说该问题是因为触发了Oracle的BUG导致,最直接的解决方法就是重启数据库实例; Linux下数据库实例重启...
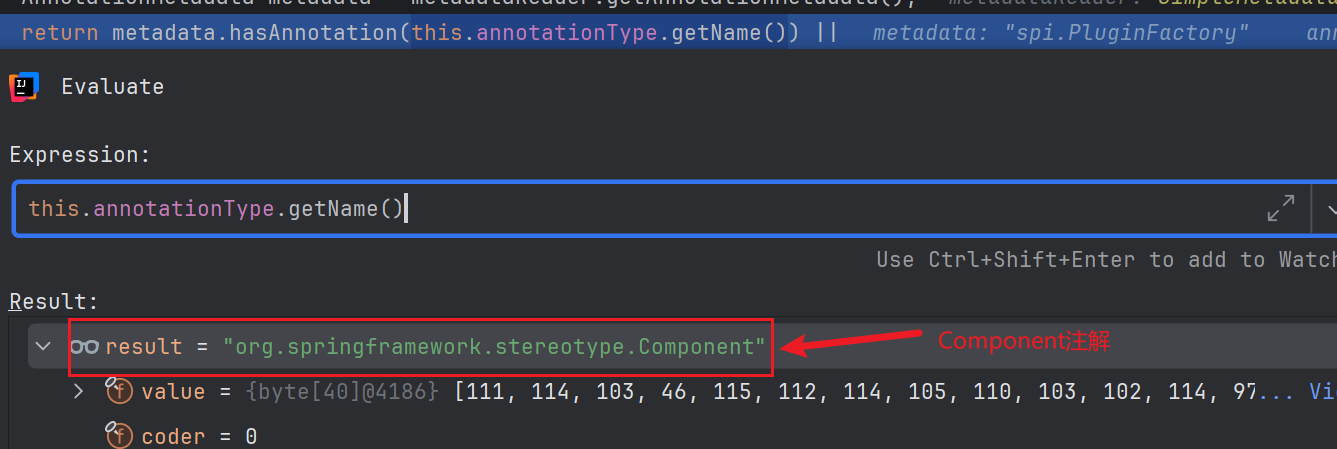
一次 Spring 扫描 @Component 注解修饰的类坑
问题现象 之前遇到过一个问题,在一个微服务的目录下有相同功能 jar 包的两个不同的版本,其中一个版本里面的类有 Component 注解,另外一个版本的类里面没有 Component 注解,且按照加载的顺序,没有 Component 注解的 j…...

深度学习:调整学习率
目录 前言 一、什么是调整学习率? 二、调整学习率的作用 三、怎么调整学习率 1.有序调整 2.自适应调整 3.自定义调整 4.调整示例 前言 在深度学习中,调整学习率是非常重要的,它对模型的训练效果和收敛速度有显著影响。 一、什么是调整…...

Java项目实战II基于Java+Spring Boot+MySQL的厨艺交流平台设计与实现(源码+数据库+文档)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。获取源码联系方式请查看文末 一、前言 在美食文化…...

第二十节:学习Redis缓存数据库实现增删改查(自学Spring boot 3.x的第五天)
这节记录下如何使用redis缓存数据库。 第一步: 先在服务器端安装redis, 下载地址:Releases tporadowski/redis GitHub。 第二步: 安装redis客户端可视化管理软件redisDesktopmanager Redis Desktop Manager - Download 第…...

Android SQLite的基本使用、生成Excel文件保存到本地
1. Android SQLite的基本使用 1.1. SQLiteOpenHelper Android 底层已经通过一个SQLiteOpenHelper的抽象类将数据库的创建,以及修改,更新等都放在了里面。 要使用它必须实现它的OnCreate(SQLiteDatabase db),onUpgrade(SQLiteDatabase db, int…...

记一次因视频编码无法在浏览器播放、编码视频报错问题
起因 ... f cv2.VideoWriter_fourcc(*h264) ...我这边使用h264编码会提示 OpenCV: FFMPEG: tag 0x34363268/h264 is not supported with codec id 27 and format mp4 / MP4 (MPEG-4 Part 14) OpenCV: FFMPEG: fallback to use tag 0x31637661/avc1 [ERROR:02.711] global /i…...
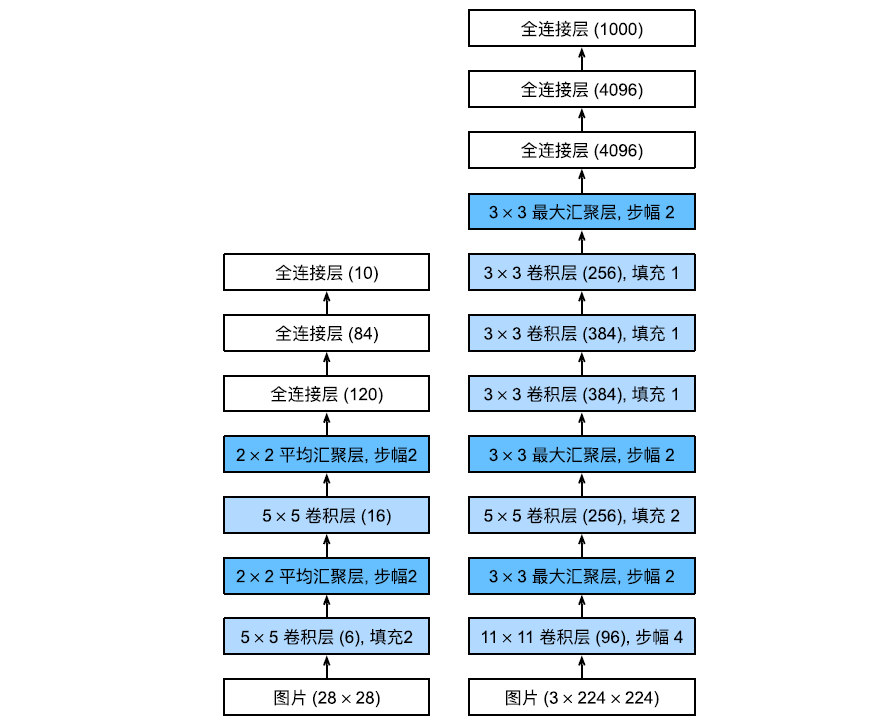
【深度学习】深度卷积神经网络(AlexNet)
在 LeNet 提出后,卷积神经网络在计算机视觉和机器学习领域中很有名气,但并未起到主导作用。 这是因为 LeNet 在更大、更真实的数据集上训练的性能和可行性还有待研究。 事实上,在 20 世纪 90 年代到 2012 年之间的大部分时间里,…...
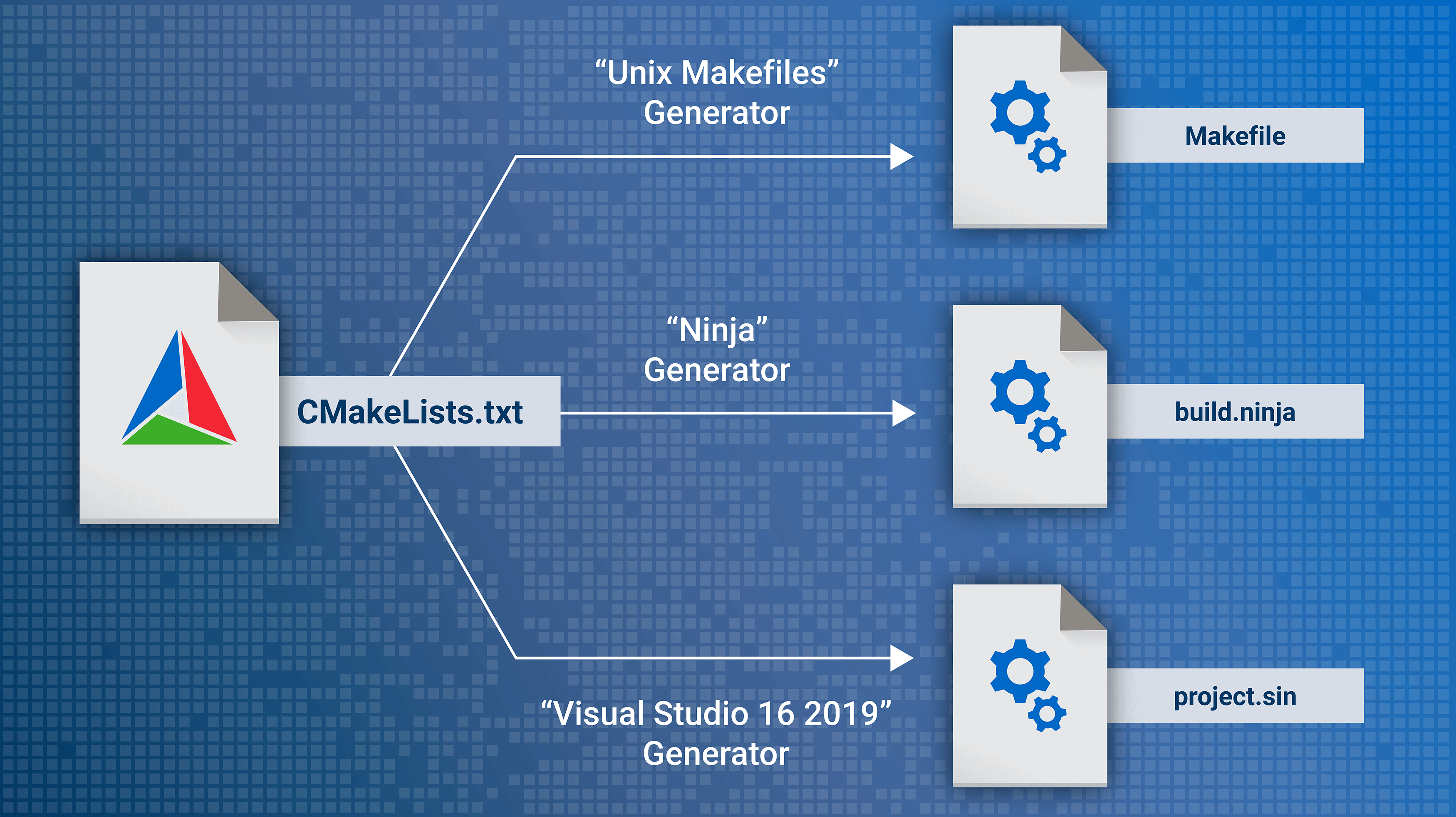
C语言扫盲
文章目录 C版本C语言特征GCCprintf数据类型函数指针内存管理void指针 Struct结构和Union结构typedef预处理器make工具cmake工具Projectintegral of sinc functionemulator embedded systeman event schedule 补充在线Linux终端安装Linux参考 建议还是国外教材学习…人家的PPT比…...
视频融合共享平台LntonAIServer视频智能分析抖动检测算法和过亮过暗检测算法
LntonAIServer作为一款智能视频监控平台,集成了多种先进的视频质量诊断功能,其中包括抖动检测和过暗检测算法。这些算法对于提升视频监控系统的稳定性和图像质量具有重要意义。 以下是对抖动检测算法和过暗检测算法的应用场景及优势的详细介绍。 一、L…...
)
【笔记篇】Davinci Configurator OS模块(上)
目录 1 简介1.1 架构概览2 功能描述2.1 特性2.2 规范偏离2.2.1 API 函数的泛型偏离2.2.2 可信函数 API 偏离2.2.3 服务保护偏离2.2.4 代码保护2.2.5 SyncScheduleTable API 偏差2.2.6 CheckTask/ISRMemoryAccess API 偏差2.2.7 中断 API 偏差2.2.8 Cross Core Getter API2.2.9 …...
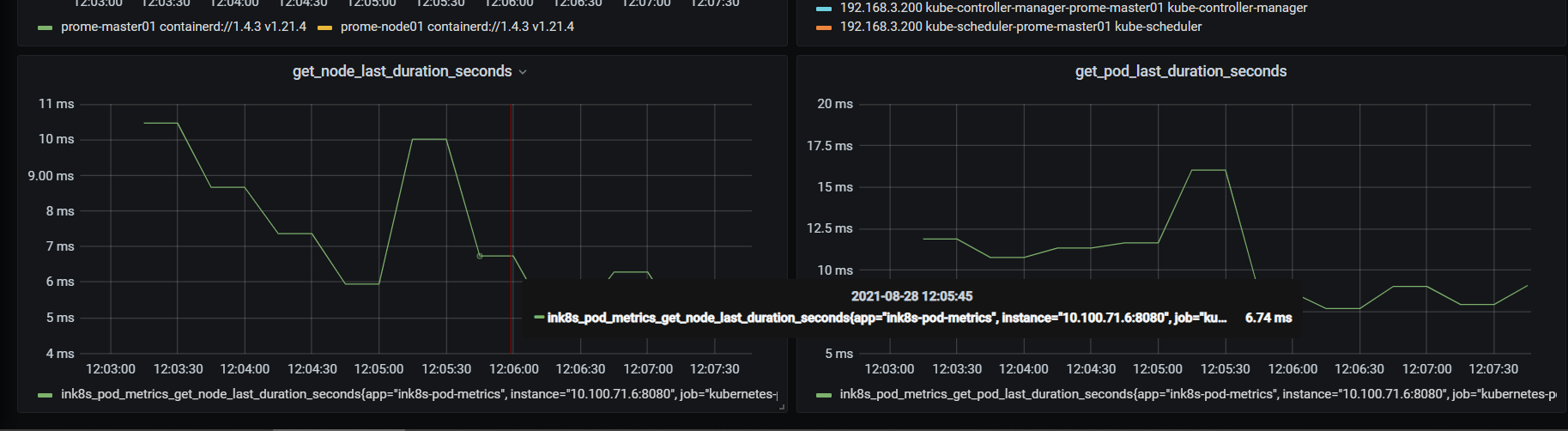
19.3 打镜像部署到k8s中,prometheus配置采集并在grafana看图
本节重点介绍 : 打镜像,导出镜像,传输到各个节点并导入运行该项目配置prometheus和grafana 打镜像 本地build docker build -t ink8s-pod-metrics:v1 .build过程 导出镜像 docker save ink8s-pod-metrics > ink8s-pod-metrics.tar 传输到各个node…...

如何让系统u盘重新可用
目录 引言开始操作遇到的错误 引言 我们将 u 盘制作为系统 U 盘后,U 盘就没法在电脑中正常识别出了。当装完系统,不再需要 u 盘充当系统 U 盘想要正常使用该 U 盘,这时候就需要有些操作,让这个 U 盘正常化。 上图就是充当系统盘的…...

14.安卓逆向-frida基础-编写hook脚本2
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于:图灵Python学院 本人写的内容纯属胡编乱造,全都是合成造假,仅仅只是为了娱乐,请不要盲目相信。 工…...

车辆零部件检测和分割数据集-车体数据集-yolo格式-yolov5-yolov10可用
这些标签是用于实例分割任务中的类别,通常在汽车图像识别或自动驾驶技术中使用。以下是这些类别: back_bumper - 后保险杠back_glass - 后挡风玻璃back_left_door - 后左车门back_left_light - 后左灯back_right_door - 后右车门back_right_light - 后右…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
