算法导论—分治法思想、动态规划思想、贪心思想
算法导论—分治法思想、动态规划思想、贪心思想
- 分治法的思想:
- 动态规划:
- 贪心算法:
- 贪心算法求解问题的条件:
- 设计贪心算法的步骤:
分治法的思想:
将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
分治模式在每层递归时都有三个步骤:
分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
解决这些子问题,递归地求解各子问题。然而,若子问题的规模足够小,则直接求解。
合并这些子问题的解成原问题的解。
归并排序算法完全遵循分治模式。直观上其操作如下:
分解:分解待排序的n个元素的序列成各具n/2个元素的两个子序列
解决:使用归并排序递归地排序两个子序列
合并:合并两个已排序的子序列以产生已排序的答案
求解递归式:
- 代入法求解
- 递归树方法
- 主方法
动态规划:
每次决策依赖于当前状态,又随即引起状态的转移。一个决策序列就是在变化的状态中产生的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。
基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一问题的解,为后一问题的求解提供了有用的信息。在求解任意子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
由于动态规划解决的问题多数有重叠子问题这个特点,为减少重复计算,对每个子问题只解一次,将其不同阶段的不同状态保存在一个二维数组中。
与分治法最大的区别是:适用于用动态规划法求解的问题,经分解后得到的子问题往往不是互相独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上)
动态规划的关键点:
1、最优化原理,也就是有最优子结构性质。这指的是一个最优化策略具有这样的性质,无论过去状态和决策如何,对前面的决策所形成的状态而言,余下的决策必须构成最优策略,简单来说就是一个最优化策略的子策略总是最优的,如果一个问题满足最优化原理,就称其具有最优子结构性质
2、无后效性,指的是某个状态下的决策的收益,只与状态和决策相关,与达到该状态的方式无关
3、子问题的重叠性,动态规划将原来指数级的暴力搜索算法改进到了具有多项式时间复杂度的算法,其中的关键在于解决了冗余、重复计算的问题
基本步骤:
- 刻画一个最优解的结构特征,如果一个问题的最优解包含其子问题的最优解,我们就称此问题具有最优子结构性质。
- 递归地定义最优解的值
- 计算最优解的值,通常采用自底向上的方法
- 利用计算出的信息构造一个最优解
多项式时间算法 (polynomial time algorithm) 表示:算法的复杂度与输入的规模呈多项式关系。
伪多项式时间算法 (pseudopolynomial time algorithm) 表示:算法的复杂度与输入规模呈指数关系,与输入的数值大小呈多项式关系。
举两个对比的例子:
冒泡排序:给定 n 个64位的数字,进行 n-1 次扫描交换,将数字从小到大排序。
素数测试:给定数字 n,通过从 2 到根号 n 的整数遍历,判断 n 是否为素数。字面上看,两者复杂度都是 O(nk)O(n^k)O(nk)( k 为整数) 。但区别在于,前者的 n 是数字个数的多少,后者的 n 是数字的大小。因此,前者输入总规模 s1 增长与数字大小无关,s1 = 64n;后者增长规模与数字大小紧密相关,输入总规模为 s2 = logn 。所以可知冒泡排序中复杂度 O(n2)=O(s12/642)O(n^2) = O(s1^2/64^2)O(n2)=O(s12/642) 为多项式算法,后者素数测试O(n)=O(2s2)O(n) = O(2^{s_2})O(n)=O(2s2)为伪多项式算法
0-1背包问题是伪多项式时间复杂度,对于具有N个项目且尺寸为W的背包的无界背包问题,运行时间为O(NW)O(NW)O(NW)。W在输入长度上不是多项式,这就是伪多项式的原因。
考虑W = 1,000,000,000,000。它仅用40位来表示该数字,因此输入大小= 40,但是计算运行时使用的因子为1,000,000,000,000,即O(240)O(2^{40})O(240)。
因此,运行时间更准确地说是O(N⋅2W)O(N·2^W)O(N⋅2W),它是指数。
贪心算法:
贪心算法求解问题的条件:
- 贪心选择性质:我们可以通过做出局部最优选择来构造全局最优解
- 最优子结构:一个问题的最优解包含其子问题的最优解
设计贪心算法的步骤:
- 将最优化问题转换形式:对其做出一次选择后,只剩下一个子问题需要求解
- 证明做出贪心选择后,原问题总是存在最优解,即贪心选择总是安全的
- 证明做出贪心选择后,剩余的子问题满足性质:其最优解与贪心选择组合即可得到原问题的最优解,这样就得到了最优子结构
相关文章:

算法导论—分治法思想、动态规划思想、贪心思想
算法导论—分治法思想、动态规划思想、贪心思想分治法的思想:动态规划:贪心算法:贪心算法求解问题的条件:设计贪心算法的步骤:分治法的思想: 将原问题分解为几个规模较小但类似于原问题的子问题࿰…...

Spring-Data-Jpa实现继承实体类
写在前面:从2018年底开始学习SpringBoot,也用SpringBoot写过一些项目。现在对学习Springboot的一些知识总结记录一下。如果你也在学习SpringBoot,可以关注我,一起学习,一起进步。 相关文章: 【Springboot系…...

多线程环境下的伪共享
今天和大家聊一聊伪共享 1.什么是伪共享? 缓存一致性协议在计算机中针对的最小单元:缓存行,每个缓存行的大小是64字节,一串连续的64字节数据都会存储到缓存行中。 假设数据A和数据B在同一缓存行中,CPU1修改了数据A&am…...

【Taylor and Francis】1/2区云计算、物联网、机器学习类,SCIEEI双检,审稿友好
机器学习类 【期刊简介】IF:6.5-7.0,JCR1/2区,中科院3区 【检索情况】SCIE&EI双检 【参考周期】2-3个月左右录用 【征稿领域】面向制造业云计算物联网应用的机器学习方法 【截稿日期】10篇版面 毕业必看-快刊 计算机科学类…...

CleanMyMac X4.12新版本下载及功能介绍
CleanMyMac X2023最新版终于迎来了又4.12,重新设计了 UI 元素,华丽的现代化风格显露无余。如今的CleanMyMac,早已不是单纯的系统清理工具。在逐渐融入系统优化、软件管理、文件管理等功能后,逐渐趋近于macOS的系统管家,…...
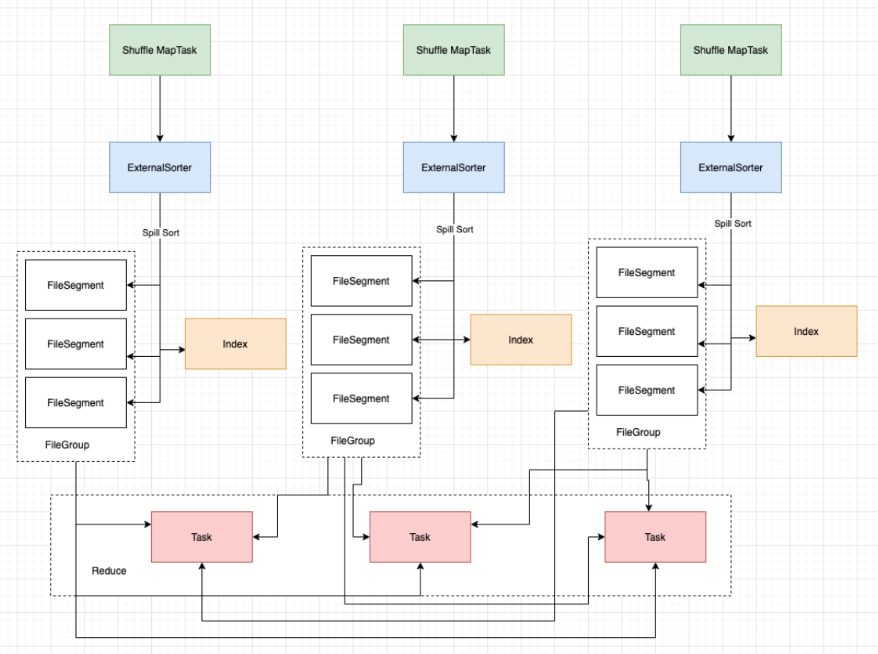
大数据技术架构(组件)26——Spark:Shuffle
2.1.6、Shuffle2.1.6.0 Shuffle Read And WriteMR框架中涉及到一个重要的流程就是shuffle,由于shuffle涉及到磁盘IO和网络IO,所以shuffle的性能直接影响着整个作业的性能。Spark其本质也是一种MR框架,所以也有自己的shuffle实现。但是和MR中的shuffle流程…...

关于Zebec生态的改进提案,即将上线的 Nautilus 链
概括 在最初作为 Solana 原生应用程序推出一年后,Zebec 团队已经能够通过在 BNB和NEAR区块链上成功部署来扩大其产品的范围。 凭借继续向尽可能多的公司/协议/基金提供薪资工具和基础设施的雄心勃勃的计划,我们决定采用最终将使 Zebec生态系统及其核心…...

Python数据可视化(三)(pyecharts)
分享一些python-pyecharts作图小技巧,用于展示汇报。 一、特点 任何元素皆可配置pyecharts只支持python原生的数据类型,包括int,float,str,bool,dict,list动态展示,炫酷的效果,给人视觉冲击力 # 安装 pip install pyecharts fr…...

【Redis面试指南】
Redis面试指南 Redis是一个开源的、基于内存的、高性能的键值对存储系统,它可以用于存储非常大量的数据,并且可以在短时间内获取数据。Redis的性能被广泛用于Web应用程序的缓存层,以提高应用程序的性能和可用性。Redis的面试是一个比较复杂的…...

大数据技术之Hadoop(生产调优手册)
第1章 HDFS—核心参数 1.1 NameNode内存生产配置 1)NameNode内存计算 每个文件块大概占用150byte,一台服务器128G内存为例,能存储多少文件块呢? 128 * 1024 * 1024 * 1024 / 150Byte ≈ 9.1亿 G MB KB Byte 2)Hadoop…...

「Vue源码学习」常见的 Vue 源码面试题,看完可以说 “精通Vue” 了吗?
Vue源码面试题一、行时(Runtime) 编译器(Compiler) vs. 只包含运行时(Runtime-only)webpackRollupBrowserify二、Vue 的初始化过程(面试关问:new Vue(options) 发生了什么࿱…...

FreeModbus RTU 移植指南
FreeModbus 简介 FreeModbus 是一个免费的软件协议栈,实现了 Modbus 从机功能: 纯 C 语言支持 Modbus RTU/ASCII支持 Modbus TCP 本文介绍 Modbus RTU 移植。 移植环境: 裸机Keil MDK 编译器Cortex-M3 内核芯片(LPC1778/88&…...
《唐诗三百首》数据源网络下载
2023年的 元宵之夜,这场以“长安”为主题的音乐会火了!在抖音,超过2300万人次观看了直播,在线同赏唐诗与交响乐的融合。许多网友惊呼,上学时那些害怕背诵的诗句,原来还可以有这么美的表达这场近80分钟的音乐…...

(深度学习快速入门)第五章第一节2:GAN经典案例之MNIST手写数字生成
获取pdf:密码7281 文章目录一:数据集介绍二:GAN简介(1)简介(2)损失函数三:代码编写(1)参数及数据预处理(2)生成器与判别器模型&#x…...
雁过留痕,竟是病毒的痕迹?
凌恩生物全新升级宏病毒组分析流程;聚焦DNA,RNA病毒组研究热点;高灵敏度检测vOTUs;多软件整合,精准鉴定病毒序列;直击地化循环关键环节,助力宏病毒组科研成功!期刊:Micro…...

Linux基本功系列之sort命令实战
文章目录前言一. sort命令介绍二. 语法格式及常用选项三. 参考案例3.1 按照文本默认排序3.2 忽略相同的行3.3 按数字大小进行排序3.4 检查文件是否已经按照顺序排序3.5 将第3列按照数字大小进行排序3.6 将排序结果输出到文件四. 探讨 -k的高级用法总结前言 大家好,…...
【笔记】移动端自动化:adb调试工具+appium+UIAutomatorViewer
学习源: https://www.bilibili.com/video/BV11p4y197HQ https://blog.csdn.net/weixin_47498728/category_11818905.html 一、移动端测试环境搭建 学习目标 1.能够搭建java 环境 2.能够搭建android 环境 (一)整体思路 我们的目标是Andr…...
面试复习题--性能检测原理
1、布局性能检测 Systrace,内存优化工具中也用到了 Systrace,这里关注 Systrace 中的 Frames 页面,正常情况下圆点为绿色,当出现黄色或者红色的圆点时,表现出现了丢帧。 Layout Inspector,是 AndroidStudio 自带工具…...

@LoadBalanced 和 @RefreshScope 同时使用,负载均衡失效分析
背景 最近引入了 Nacos Config 配置管理能力,说起来用法很简单,还是踩了三个坑。 Nacos Config 的 nacos 的帐号密码加密配置后,怎么解密而且在 NacosConfigBootstrapConfiguration 真正注入 Nacos Config 注入之前,而且不能触发…...

2023年个人计划
2023年个人计划 可能是最近太清闲,感觉生活很无聊,就胡乱做下新年的规划吧,扰乱下烦闷的心 1 二宝健健康康,活泼可爱 目前老婆已经怀孕5周左右了,二宝将在进行年中降生,希望老婆少受点罪,二宝…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
