【笔记】原子结构的近代理论
近代原子结构理论的建立是从氢原子光谱得到启示的。
一、氢原子光谱与波尔理论
1.氢原子光谱
在装有两个电极的真空玻璃管内通入极少量高纯氢气,通高压电使之放电,管中发出的光束通过分光棱镜,得到分立的谱线,称为线状光谱。
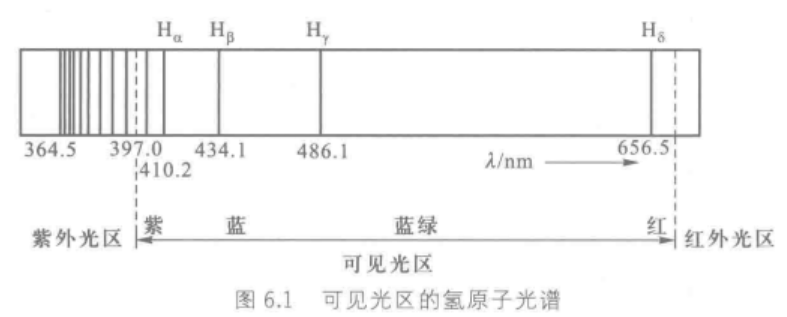
发现氢原子光谱中谱线的频率满足里德伯方程式: ν = 3.29 × 1 0 15 ( 1 n 1 2 − 1 n 2 2 ) , n 1 > n 2 \nu=3.29\times 10^{15}(\frac1{n_1^2}-\frac1{n_2^2}),n_1>n_2 ν=3.29×1015(n121−n221),n1>n2
为了解释氢原子光谱,把普朗克的量子论应用于卢瑟福的含核原子模型,得到玻尔原子模型。
2.波尔原子模型
-
电子在核外只能沿着特定的轨道而不是任意圆轨道运动,在这些轨道上运动的电子不放出也不吸收能量。
求电子绕核运动的轨道半径: r n = a 0 n 2 r_n=a_0n^2 rn=a0n2,n是主量子数, a 0 = 53 p m a_0=53pm a0=53pm,称为玻尔半径。
求电子能量: E = − 2.18 × 1 0 − 18 n 2 E=-\frac{2.18\times 10^{-18}}{n^2} E=−n22.18×10−18
在通常情况下,电子尽可能在离核最近、能量最低的n=1轨道上运动,处于“基态”;电子在其他轨道上运动,处于“激发态”; n = ∞ , E ∞ = 0 n=\infin,E_{\infin}=0 n=∞,E∞=0,电子被电离成为自由电子。
-
原子中的电子由一个轨道跃迁到另一个轨道时才会放出或吸收能量。若能量以光辐射的形式出现,其频率取决于两个轨道之间的能极差。
h ν = E n 2 − E n 1 h\nu=E_{n_2}-E_{n_1} hν=En2−En1
推出氢原子光谱的频率是 ν = 3.29 × 1 0 15 ( 1 n 1 2 − 1 n 2 2 ) \nu=3.29\times 10^{15}(\frac1{n_1^2}-\frac1{n_2^2}) ν=3.29×1015(n121−n221)
波尔理论虽然成功解释了氢原子光谱,但是不能解释多电子原子的光谱甚至不能解释氢原子光谱的精细结构。
它没有完全冲破经典物理的束缚,没有意识到电子运动的特性——波粒二象性,因此不能全面反映微观粒子的运动规律。
二、微观粒子运动的波粒二象性和统计规律
光的干涉、衍射——波动性
光电效应——粒子性
德布罗意认为电子也和光子一样具有波动性,通过德布罗意关系式计算波长: λ = h m v \lambda=\frac h{mv} λ=mvh
电子在晶体上的衍射证实了德布罗意预言,在屏幕上产生圆环衍射。
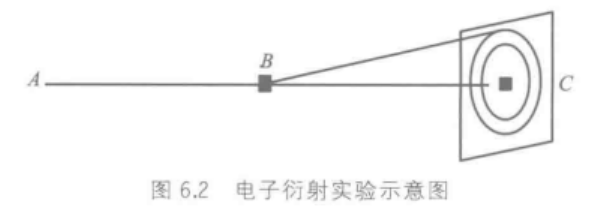
德布罗意波/物质波:微观粒子具有的波。
三、薛定谔方程和波函数
为了描述核外电子运动状态而建立的薛定谔方程,形式是一个二阶偏微分方程。
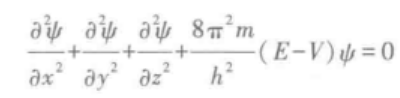
其中x、y、z表示电子的空间直角坐标;m是电子的质量;E是系统总能量;V是核对电子的吸引能,即势能;ψ是三维坐标x、y、z的函数,称为波函数。
薛定谔方程的意义:每一个合理解ψ就代表该微粒运动的某一种可能,对应的E就是该定态对应的能级。
波函数ψ近似认为核外电子可能出现的区域,被称为原子轨道,又称原子轨函(和宏观轨道区别)。
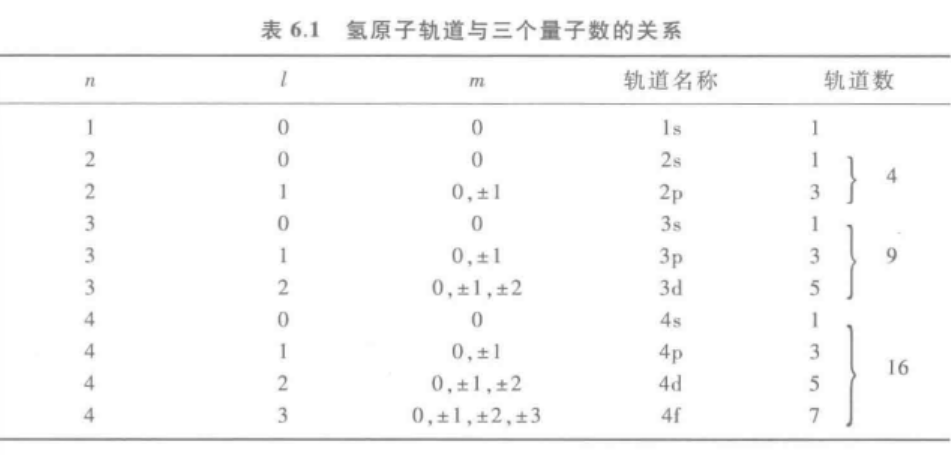
1.四个量子数及含义
求解薛定谔方程不仅可以导出E和n,还可以导出三个量子数:主量子数n、角量子数l、磁量子数m
当这三个量子数确定,波函数ψ才有合理解。故n、l、m三量子数被称为轨道量子数。
(1)主量子数n
n是决定原子轨道能级的主要参数,表示不同的电子主层。
n的数值越大,电子的能量越高,电子离核距离越远。
n=1,2,……正整数
通常用K、L、M、N、O、P表示电子层:
| 主量子数n | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|
| 电子层 | K | L | M | N | O | P | … |
能量高低顺序: K<L<M<N<O<P<…
(2)角量子数l
在高分辨分光镜下,可以观察到一些元素原子光谱的一条粗谱线由多条很靠近的细谱线构成,说明同一电子层内电子的运动状态和能量不是完全相同,这是因为不同的原子轨道,同一电子层还可以分成几个不同的亚层。
l是反映原子轨道形状的参数。
l取值受n的限制。l=0,1,2,…,n-1正整数
亚层符号为s,p,d,f
| 角量子数l | 0 | 1 | 2 | 3 | …… |
|---|---|---|---|---|---|
| 亚层符号 | s | p | d | f | … |
| 原子轨道形状 | 球形 | 哑铃形 | 梅花瓣型 | (无解) | … |
(3)磁量子数m
激发态原子在外磁场作用下,原来的一条谱线还可以分裂成若干条,这是由于同一个亚层可以有多个原子轨道(只有空间伸展方向不同的区别)。
m是用来描述原子轨道在空间伸展方向的参数。
m取值受l的制约,取值范围为:[-l,l]的整数值
简并轨道/等价轨道:亚层中具有的方向不同的轨道在没有外加磁场的情况下,具有相同的能量。
(4)自旋量子数 m s m_s ms
m s m_s ms用来描述电子运动的自旋方向。
m s m_s ms只有两种可能的取值, ± 1 2 \pm\frac12 ±21,通常用向上↑或向下↓的箭头表示。
自旋反平行:两个电子处于不同的自旋状态,可用符号"↑↓","↓↑"表示。
自旋平行:两个电子处于相同的自旋状态,用符号“↑↑”或“↓↓”表示。
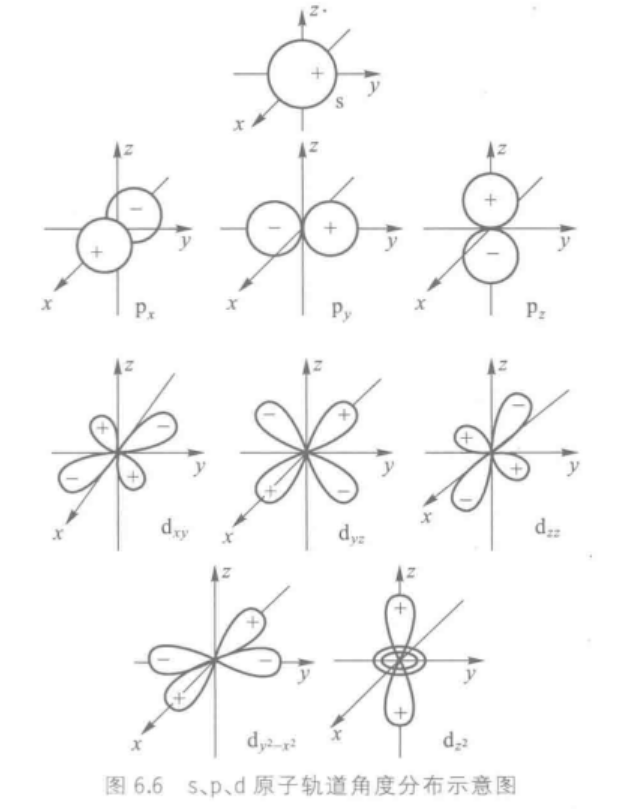
2.原子轨道的角度分布图
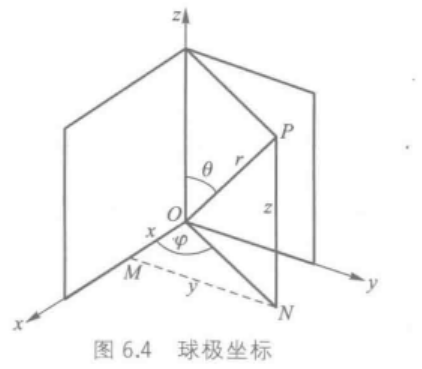
ψ既可以用直角坐标ψ(x,y,z)表示,也可以变换成球极坐标ψ(r,θ,φ)表示。
x = r s i n θ c o s ϕ y = r s i n θ s i n ϕ z = r c o s θ ψ ( r , θ , ϕ ) = R ( r ) ⋅ Y ( θ , ϕ ) x=rsin\theta cos\phi\\ y=rsin\theta sin\phi\\ z=rcos\theta\\ \psi(r,\theta,\phi)=R(r)\cdot Y(\theta,\phi) x=rsinθcosϕy=rsinθsinϕz=rcosθψ(r,θ,ϕ)=R(r)⋅Y(θ,ϕ)
其中, R ( r ) R(r) R(r)代表径向部分, Y ( θ , ϕ ) Y(\theta,\phi) Y(θ,ϕ)代表原子轨道的角度部分。
已知波函数如下:

1s轨道
Y 1 s Y_{1s} Y1s取值是定值 1 4 π \sqrt{\frac1{4\pi}} 4π1,跟角度没关系,所以它们的角度分布图是一个半径为 1 4 π \sqrt{\frac1{4\pi}} 4π1的球面, Y 1 s Y_{1s} Y1s值在各个方向相同。
所有s轨道波函数都跟1s相同,都为 1 4 π \sqrt{\frac1{4\pi}} 4π1,所以角度分布图都是半径为 1 4 π \sqrt{\frac1{4\pi}} 4π1的球面。
2 p z 2p_z 2pz轨道
Y p z = 3 4 π c o s θ Y_{p_z}=\sqrt{\frac3{4\pi}}cos\theta Ypz=4π3cosθ
在球坐标中作图,可得到两个相切于原点的球面,即为 p z p_z pz轨道的角度分布图。
另外两个 p x p_x px, p y p_y py形状和 p z p_z pz相同,只是空间取向不同。
四、电子云
1.电子云与概率密度
概率密度:电子在原子核外空间某位置上单位体积出现的概率大小。
在光学中,光的强度与电磁场强度的绝对值平方成正比,类比到电子,就是在原子核外某处空间发现电子的概率密度ρ和电子波在此处的强度ψ的绝对值的平方成正比, ρ ∝ ∣ ψ ∣ 2 \rho\propto |\psi|^2 ρ∝∣ψ∣2
在研究中,有实际意义的是相对密度而非绝对密度,故只需要考虑电子波在此处的强度的平方即可,用 ∣ ψ ∣ 2 |\psi|^2 ∣ψ∣2表示核外电子出现的概率密度。
2.电子云角度分布图
电子云的图形可以类比原子轨道,分为两部分(径向+角度)
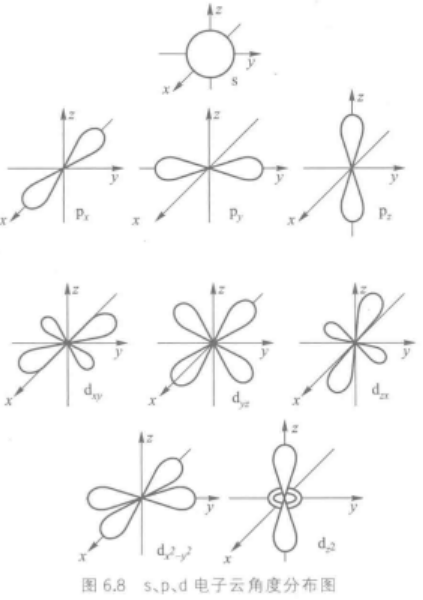
3.电子云径向分布图
电子云角度分布图只能表现出电子在空间不同角度出现的概率大小,不能表现电子出现概率和离核远近的关系,所以需要电子云径向分布图。
电子云径向分布图:在半径为r,厚度为dr的球壳,电子出现的概率(即 4 π r 2 R 2 d r 4\pi r^2R^2dr 4πr2R2dr或 r 2 R 2 d r r^2R^2dr r2R2dr的大小)。以 4 π r 2 R 2 d r 4\pi r^2R^2dr 4πr2R2dr对r作图得到。
4 π r 2 R 2 d r 4\pi r^2R^2dr 4πr2R2dr数值越大,表示电子在半径为r的球壳中出现的概率越大。
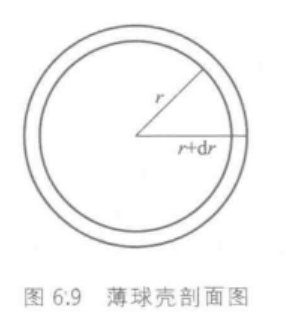
从电子云径向分布看出:n增大时,电子离核平均距离增大;当n相同,电子离核平均距离接近。
相关文章:

【笔记】原子结构的近代理论
近代原子结构理论的建立是从氢原子光谱得到启示的。 一、氢原子光谱与波尔理论 1.氢原子光谱 在装有两个电极的真空玻璃管内通入极少量高纯氢气,通高压电使之放电,管中发出的光束通过分光棱镜,得到分立的谱线,称为线状光谱。 发…...

【python】循环中断:break 和 continue
目录: while 循环的基础语法while 循环的基础案例while 循环的嵌套应用while 循环的嵌套案例for 循环的基础语法for 循环的嵌套应用循环中断:break 和 continue综合案例 学习目标: 掌握使用 continue 和 break 关键字控制循环 思考&#…...

WIFI密码默认显示
文章目录 需求分析遇到问题问题原因解决方案 需求 在进入设置,点击某一个wifi,连接wifi 界面,显示密码默认选中状态,效果如下 分析 在 WiFi密码被输入法挡住 中我们已经分析了整个流程,布局文件和控制中心。 结局系统设置WIFI连…...

Emiya 家今天的饭C++
题目: 样例解释: 【样例 1 解释】 由于在这个样例中,对于每组 i,j,Emiya 都最多只会做一道菜,因此我们直接通过给出烹饪方法、主要食材的编号来描述一道菜。 符合要求的方案包括: 做一道用烹饪方法 1、主要…...

Mybatis缓存机制(图文并茂!)
目录 一级缓存 需求我们在一个测试中通过ID两次查询Monster表中的信息。 二级缓存 案例分许(和上述一样的需求) EhCache第三方缓存 在了解缓存机制之前,我们要先了解什么是缓存: 缓存是一种高速存储器,用于暂时存储访问频繁的数据&…...

Git 工作区、暂存区和版本库
Git 工作区、暂存区和版本库 Git 是一个强大的版本控制系统,它帮助开发者管理代码历史,协作开发,以及跟踪和合并更改。为了更好地理解 Git 的工作流程,我们需要了解 Git 中的三个核心概念:工作区(Workspac…...

SSH 远程连接到 Linux 服务器上的 SQLite
通过 SSH 远程连接到 Linux 服务器上的 SQLite 数据库文件的流程,可以分为以下几个步骤: 通过 SSH 连接到远程 Linux 服务器。在远程服务器上执行 SQLite 命令行工具,操作数据库文件。在本地使用工具,通过 SSH 隧道间接访问远程的…...

使用ElasticSearch-dump工具进行ES数据迁移、备份
elasticsearch-dump基本使用 该工具基于第三方Elasticdump工具来实现,仓库地址:https://github.com/elasticsearch-dump/elasticsearch-dump/tree/master,用于更加快捷方便的将Elasticsearch不同集群的数据进行索引备份和还原。 一、安装 …...

SpringMVC源码-SpringMVC源码请求执行流程及重点方法doDispatch讲解
一、开始请求 在浏览器访问http://localhost:8080/spring_mymvc/userlist这个接口,是个get请求。 FrameworkServlet类的service方法会被请求到: 调用路径如下: service:945, FrameworkServlet (org.springframework.web.servlet) service:764, HttpSer…...

《深度学习》OpenCV 指纹验证、识别
目录 一、指纹验证 1、什么是指纹验证 2、步骤 1)图像采集 2)图像预处理 3)特征提取 4)特征匹配 5)相似度比较 6)结果输出 二、案例实现 1、完整代码 2、实现结果 调试模式: 三、…...
爬虫入门之爬虫原理以及请求响应
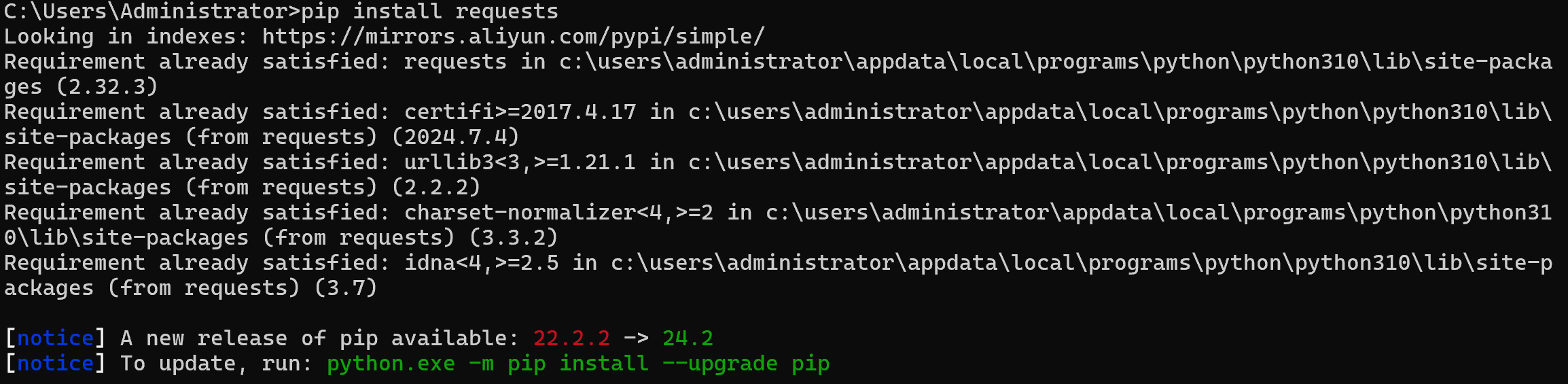
爬虫入门之爬虫原理以及请求响应 爬虫需要用到的库, 叫requests. 在导入requests库之前, 需要安装它, 打开cmd: 输入pip install 库名 pip install requests后面出现successful或requirement already就说明已经下载成功了!!! 下载出现的问题: 1.有报错或者是下载慢 修改镜像…...

CTF ciscn_2019_web_northern_china_day1_web1复现
ciscn_2019_web_northern_china_day1_web1 复现,环境源于CTFTraining 分析 拿到题目扫描,发现没有什么有用资产 扫描过程中注册账号登录,发现上传入口 上传文件,发现下载删除行为,寻找功能点,发现不能访问…...

docker命令汇总
Docker 是一个开源的应用容器引擎,它允许开发者打包应用以及依赖包到一个可移植的容器中,然后发布到任何流行的 Linux 机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有任何接口。 以下是一些常用的 Docker 命令…...

云计算在现代企业中的应用与优势
云计算在现代企业中的应用与优势 随着信息技术的飞速发展,云计算已经成为现代企业不可或缺的一部分。作为一种创新的计算模式,云计算为企业提供了前所未有的灵活性和可扩展性,极大地推动了企业的数字化转型。 一、云计算的基本概念 云计算…...

Android平台GB28181实时回传流程和技术实现
规范解读 GB28181 中的 “INVITE” 是会话初始协议(SIP)中的一种请求方法,主要用于邀请一个或多个参与者加入特定的会话。在 GB28181 标准中,“INVITE” 请求通常用于发起媒体流的传输请求。当一个设备想要接收来自另一个设备的媒…...

Text-to-SQL方法研究
有关Text-to-SQL实现细节,可以查阅我的另一篇文章text-to-sql将自然语言转换为数据库查询语句 1、面临的挑战 自然语言问题往往包含复杂的语言结构,如嵌套语句、倒装句和省略等,很难准确映射到SQL查询上。此外,自然语言本身就存在歧义,一个问题可能有多种解读。消除…...
功能介绍及实现)
【Router】路由功能之MAC地址过滤(MAC Filter)功能介绍及实现
MAC地址过滤(MAC Filter) MAC 地址过滤是一种网络安全技术,通过在网络设备(如路由器)上设置规则,允许或阻止特定 MAC 地址的设备连接到网络。其主要作用是增强网络的安全性,防止未经授权的设备接入网络。 MAC Filter工作原理 MAC 地址过滤的工作原理是根据设备…...

Flink 本地 idea 调试开启 WebUI
Flink 本地 idea 调试开启 WebUI Maven 引用相关的包配置端口使用本地带UI环境启动 // maven 导入<!-- flink运行时的webUI --><dependency><groupId>org.apache.flink</groupId><artifactId>flink-runtime-web</artifactId><version…...

如何识别IP地址是独享的还是共享的
在网络环境中,IP地址的分配和使用方式直接影响到用户的在线隐私和访问安全。选择独享IP还是共享IP取决于用户的具体需求,理解这两种IP地址的差异及其特点至关重要。本文将探讨如何区分独享IP和共享IP,以及各自的优缺点。 1. 什么是独享IP与共…...

X-Spreadsheet使用教程:打造你的Web端电子表格应用
在Web开发中,经常需要处理数据表格的展示与编辑,而X-Spreadsheet作为一款轻量级、功能强大的JavaScript电子表格库,为开发者提供了一个便捷的解决方案。本文将详细介绍如何使用X-Spreadsheet在Web项目中创建和配置电子表格,让你的…...

如何利用d3-interpolate打造React-Move高级动画:完整插值技术指南
如何利用d3-interpolate打造React-Move高级动画:完整插值技术指南 【免费下载链接】react-move React Move | Beautiful, data-driven animations for React 项目地址: https://gitcode.com/gh_mirrors/re/react-move React-Move是一个基于React的数据驱动动…...

Schej.it高级使用技巧:如何利用文件夹功能组织多个会议
Schej.it高级使用技巧:如何利用文件夹功能组织多个会议 【免费下载链接】timeful.app schej helps you quickly find the best time for your group to meet. Its like When2meet with Google Calendar integration! 项目地址: https://gitcode.com/gh_mirrors/sc…...

music-metadata完全指南:从安装到高级API调用的完整教程
music-metadata完全指南:从安装到高级API调用的完整教程 【免费下载链接】music-metadata Stream and file based music metadata parser for node. Supporting a wide range of audio and tag formats. 项目地址: https://gitcode.com/gh_mirrors/mu/music-metad…...

Learnhouse SCORM集成教程:打造交互式学习体验
Learnhouse SCORM集成教程:打造交互式学习体验 【免费下载链接】learnhouse The Next-Gen Open Source learning platform ✨ 项目地址: https://gitcode.com/gh_mirrors/le/learnhouse Learnhouse作为下一代开源学习平台,提供了强大的SCORM集成功…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
