双指针---(部分地更新)
双指针

复写零
给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
示例 1:
输入:arr = [1,0,2,3,0,4,5,0]
输出:[1,0,0,2,3,0,0,4]
解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]
示例 2:
输入:arr = [1,2,3]
输出:[1,2,3]
解释:调用函数后,输入的数组将被修改为:[1,2,3]
提示:
1 <= arr.length <= 1040 <= arr[i] <= 9
题目解析:
特别需要注意的是就地
算法原理:

代码如下:
class Solution
{
public:void duplicateZeros(vector<int>& arr) {//1.先找到最后一个数int cur=0,dest=-1,n=arr.size();while(cur<n){if(arr[cur]) dest++;else dest+=2;if(dest>=n-1) break;cur++;}//2.处理边界情况if(dest==n){arr[n-1]=0;cur--;dest-=2;}//3.从后往前进行复写操作while(cur>=0){if(arr[cur]) arr[dest--]=arr[cur--];else{arr[dest--]=0;arr[dest--]=0;cur--;}}}
};
写这类题目的时候,不要在脑袋里面空想,要动手动笔去思考,像下面这样:
更详细点来说:
如果「从前向后」进⾏原地复写操作的话,由于 0 的出现会复写两次,导致没有复写的数「被覆 盖掉」。因此我们选择「从后往前」的复写策略。
但是「从后向前」复写的时候,我们需要找到「最后⼀个复写的数」,因此我们的⼤体流程分两 步:
i. 先找到最后⼀个复写的数;
ii. 然后从后向前进⾏复写操作。
算法流程:
a. 初始化两个指针 cur = 0 , dest = -1 ;
b. 找到最后⼀个复写的数:
i. 当 cur < n 的时候,⼀直执⾏下⾯循环:
• 判断 cur 位置的元素:
◦ 如果是 0 的话, dest 往后移动两位;
◦ 否则, dest 往后移动⼀位。
• 判断 dest 时候已经到结束位置,如果结束就终⽌循环;
• 如果没有结束, cur++ ,继续判断。
c. 判断 dest 是否越界到 n 的位置:
i. 如果越界,执⾏下⾯三步:
- n - 1 位置的值修改成 0 ;
- cur 向移动⼀步;
- dest 向前移动两步。
d. 从 cur 位置开始往前遍历原数组,依次还原出复写后的结果数组:
i. 判断 cur 位置的值:
- 如果是 0 : dest 以及 dest - 1 位置修改成 0 , dest -= 2 ;
- 如果⾮零: dest 位置修改成 0 , dest -= 1 ;
ii. cur-- ,复写下⼀个位置。
快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
1 <= n <= 231 - 1
题目解析:

这个题目让我们想到了带环链表
就可以考虑快慢指针来解决
算法原理:

这个题目不需要考虑是否遇不到1,或者是循环,我们可以想到鸽巢原理

联系到这个题目,我们可以知道如果哪个数回不到1,那么它一定会落到哪个环里
代码如下:
class Solution
{int Add(int n){int sum=0;while(n){int t=n%10;sum+=t*t;n/=10;}return sum;}
public:bool isHappy(int n) {int slow =n,fast=Add(n);while(slow!=fast){slow=Add(slow);fast=Add(Add(fast));}return slow==1;}
};
更进一步来说:
题⽬分析:
为了⽅便叙述,将「对于⼀个正整数,每⼀次将该数替换为它每个位置上的数字的平⽅和」这⼀个 操作记为 x 操作;
题⽬告诉我们,当我们不断重复 x 操作的时候,计算⼀定会「死循环」,死的⽅式有两种:
▪ 情况⼀:⼀直在 1 中死循环,即 1 -> 1 -> 1 -> 1…
▪ 情况⼆:在历史的数据中死循环,但始终变不到 1
由于上述两种情况只会出现⼀种,因此,只要我们能确定循环是在「情况⼀」中进⾏,还是在「情 况⼆」中进⾏,就能得到结果。
简单证明:
a. 经过⼀次变化之后的最⼤值 9^2 * 10 = 810 ( 2^31-1=2147483647 。选⼀个更⼤的最 ⼤ 9999999999 ),也就是变化的区间在 [1, 810] 之间;
b. 根据「鸽巢原理」,⼀个数变化 811 次之后,必然会形成⼀个循环;
c. 因此,变化的过程最终会⾛到⼀个圈⾥⾯,因此可以⽤「快慢指针」来解决。
解法(快慢指针):
算法思路:
根据上述的题⽬分析,我们可以知道,当重复执⾏ x 的时候,数据会陷⼊到⼀个「循环」之中。
⽽「快慢指针」有⼀个特性,就是在⼀个圆圈中,快指针总是会追上慢指针的,也就是说他们总会 相遇在⼀个位置上。如果相遇位置的值是 1 ,那么这个数⼀定是快乐数;如果相遇位置不是 1 的话,那么就不是快乐数。
补充知识:如何求⼀个数 n 每个位置上的数字的平⽅和。
a. 把数 n 每⼀位的数提取出来:
循环迭代下⾯步骤:
i. int t = n % 10 提取个位;
ii. n /= 10 ⼲掉个位;
直到 n 的值变为 0 ;
b. 提取每⼀位的时候,⽤⼀个变量 sum 记录这⼀位的平⽅与之前提取位数的平⽅和
▪ sum = sum + t * t
盛水最多的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
示例 1:

输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
算法原理

代码如下:
class Solution
{
public:int maxArea(vector<int>& height) {int left=0,right=height.size()-1,ret=0;while(left<right){int v=min(height[left],height[right])*(right-left);ret=max(ret,v);//移动指针if(height[left]<height[right]) left++;else right--;}return ret;}
};
进一步来说:
解法⼀(暴⼒求解)(会超时):
算法思路:
枚举出能构成的所有容器,找出其中容积最⼤的值。
◦ 容器容积的计算⽅式:
设两指针 i , j ,分别指向⽔槽板的最左端以及最右端,此时容器的宽度为 j - i 。由于 容器的⾼度由两板中的短板决定,因此可得容积公式 : v = (j - i) * min( height[i], height[j])
算法代码:
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int ret = 0;// 两层 for 枚举出所有可能出现的情况for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {// 计算容积,找出最⼤的那⼀个ret = max(ret, min(height[i], height[j]) * (j - i));}}
return ret;}
};解法⼆(对撞指针):
算法思路:
设两个指针 left , right 分别指向容器的左右两个端点,此时容器的容积 :
v = (right - left) * min( height[right], height[left])
容器的左边界为 height[left] ,右边界为 height[right] 。
为了⽅便叙述,我们假设「左边边界」⼩于「右边边界」。
如果此时我们固定⼀个边界,改变另⼀个边界,⽔的容积会有如下变化形式:
◦ 容器的宽度⼀定变⼩。
◦ 由于左边界较⼩,决定了⽔的⾼度。如果改变左边界,新的⽔⾯⾼度不确定,但是⼀定不会超 过右边的柱⼦⾼度,因此容器的容积可能会增⼤。
◦ 如果改变右边界,⽆论右边界移动到哪⾥,新的⽔⾯的⾼度⼀定不会超过左边界,也就是不会 超过现在的⽔⾯⾼度,但是由于容器的宽度减⼩,因此容器的容积⼀定会变⼩的。
由此可⻅,左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界,继 续去判断下⼀个左右边界。
当我们不断重复上述过程,每次都可以舍去⼤量不必要的枚举过程,直到 left 与 right 相 遇。期间产⽣的所有的容积⾥⾯的最⼤值,就是最终答案
有效三角形的个数
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
示例 1:
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
示例 2:
输入: nums = [4,2,3,4]
输出: 4
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
这道题也是同理,不能够用脑袋空想,需要动手去梳理逻辑关系
如下图:

题目解析

这里需要注意的是不同顺序但是相同的数字也被算作是一种
算法原理

代码如下:
class Solution
{
public:int triangleNumber(vector<int>& nums) {//1.优化sort(nums.begin(),nums.end());//2.利用双指针解决问题int ret=0,n=nums.size();for(int i=n-1;i>=2;i--)//先固定最大的数{//利用双指针快速统计符合要求的三元组的个数int left=0,right=i-1;while(left<right){if(nums[left]+nums[right]>nums[i]){ret+=right-left;right--;}else{left++;}}}return ret;}};
进一步来说:
解法⼀(暴⼒求解)(会超时):
算法思路:
三层 for 循环枚举出所有的三元组,并且判断是否能构成三⻆形。
虽然说是暴⼒求解,但是还是想优化⼀下:
判断三⻆形的优化:
▪ 如果能构成三⻆形,需要满⾜任意两边之和要⼤于第三边。但是实际上只需让较⼩的两条边 之和⼤于第三边即可。、
▪ 因此我们可以先将原数组排序,然后从⼩到⼤枚举三元组,⼀⽅⾯省去枚举的数量,另⼀⽅ ⾯⽅便判断是否能构成三⻆形。
算法代码:
class Solution {
public:int triangleNumber(vector<int>& nums) {// 1. 排序sort(nums.begin(), nums.end());int n = nums.size(), ret = 0;// 2. 从⼩到⼤枚举所有的三元组for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {for (int k = j + 1; k < n; k++) {// 当最⼩的两个边之和⼤于第三边的时候,统计答案if (nums[i] + nums[j] > nums[k])ret++;} }}return ret;}
};
解法⼆(排序 + 双指针):
算法思路:
先将数组排序。
根据「解法⼀」中的优化思想,我们可以固定⼀个「最⻓边」,然后在⽐这条边⼩的有序数组中找 出⼀个⼆元组,使这个⼆元组之和⼤于这个最⻓边。由于数组是有序的,我们可以利⽤「对撞指 针」来优化。
设最⻓边枚举到 i 位置,区间 [left, right] 是 i 位置左边的区间(也就是⽐它⼩的区 间):
◦ 如果 nums[left] + nums[right] > nums[i] :
▪ 说明 [left, right - 1] 区间上的所有元素均可以与 nums[right] 构成⽐ nums[i] ⼤的⼆元组
▪ 满⾜条件的有 right - left 种
▪ 此时 right 位置的元素的所有情况相当于全部考虑完毕, right-- ,进⼊下⼀轮判断
◦ 如果 nums[left] + nums[right] <= nums[i] :
▪ 说明 left 位置的元素是不可能与 [left + 1, right] 位置上的元素构成满⾜条件 的⼆元组
▪ left 位置的元素可以舍去, left++ 进⼊下轮循环
和为s的两个数字
题⽬描述:
输⼊⼀个递增排序的数组和⼀个数字 s ,在数组中查找两个数,使得它们的和正好是 s 。如果有多 对数字的和等于 s ,则输出任意⼀对即可。
⽰例 1:
输⼊: nums = [2,7,11,15], target = 9
输出: [2,7] 或者 [7,2]
找 出⼀个⼆元组,使这个⼆元组之和⼤于这个最⻓边。由于数组是有序的,我们可以利⽤「对撞指 针」来优化。
设最⻓边枚举到 i 位置,区间 [left, right] 是 i 位置左边的区间(也就是⽐它⼩的区 间):
◦ 如果 nums[left] + nums[right] > nums[i] :
▪ 说明 [left, right - 1] 区间上的所有元素均可以与 nums[right] 构成⽐ nums[i] ⼤的⼆元组
▪ 满⾜条件的有 right - left 种
▪ 此时 right 位置的元素的所有情况相当于全部考虑完毕, right-- ,进⼊下⼀轮判断
◦ 如果 nums[left] + nums[right] <= nums[i] :
▪ 说明 left 位置的元素是不可能与 [left + 1, right] 位置上的元素构成满⾜条件 的⼆元组
▪ left 位置的元素可以舍去, left++ 进⼊下轮循环
相关文章:

双指针---(部分地更新)
双指针 复写零 给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。 注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。 …...

【Windows】自定义显示器的分辨率
背景 由于本人更新驱动导致2个显示器里面,有一个显示器的分辨率只剩下2个可以调节 这样就导致2个显示器分辨率不同,更新了多次驱动都修复不了,所以想着看能不能自定义分辨率 工具下载 显示器自定义分辨率工具 或者百度搜索 Custom Resolu…...

组播基础-2-IGMP协议
文章目录 IGMPIGMPv1IGMPv2IGMPv3IGMP总结IGMP Snooping IGMP 运行于主机和路由器之间 因特网组管理协议,TCP/IP 协议族中负责 IP 组播成员管理的协议,用来在接收者与其他直接相邻的组播路由器之间建立、维护组播组成员关系 负责组播成员管理…...

基于Springboot+Vue的视频点播系统设计与实现登录 (含源码数据库)
1.开发环境 开发系统:Windows10/11 架构模式:MVC/前后端分离 JDK版本: Java JDK1.8 开发工具:IDEA 数据库版本: mysql5.7或8.0 数据库可视化工具: navicat 服务器: SpringBoot自带 apache tomcat 主要技术: Java,Springboot,mybatis,mysql,vue 2.视频演示地址 3.功能 系统中…...

执行力怎么培养?
执行力怎么培养? 并行:适合在初期养成习惯,不抱对结果的期望天才就是强迫症:适合中期修身:适合高级 并行:适合在初期养成习惯,不抱对结果的期望 在你开始做任何事情的时候,不要一开…...

Power apps:一次提交多项申请
1、添加一个Form,导入sharepoint列表,添加确认,继续,取消按钮 2、在页面的onvisible属性中添加 Set(applynumber,Last(付款申请表).申请编号1); #定义一个申请编号变量,每次申请,就将列表最后一个…...

Oracle数据库物理结构操作管理
实验步骤 (1)查询数据库初始化参数中参数名包含sga的参数的名称、值和描述信息。 SQL> select name,value,description from V$PARAMETER where name like %sga%; (2)设置sga_max_size的大小为1G SQL> alter system set sg…...

Python自然语言处理之spacy模块介绍、安装与常见操作案例
文章目录 spacy模块介绍安装spacy常见操作案例及代码1. 加载模型并处理文本2. 词性标注3. 命名实体识别4. 依存句法分析5. 可视化(在Jupyter Notebook中) spacy模块介绍 spacy是一个强大的Python库,用于自然语言处理(NLP…...
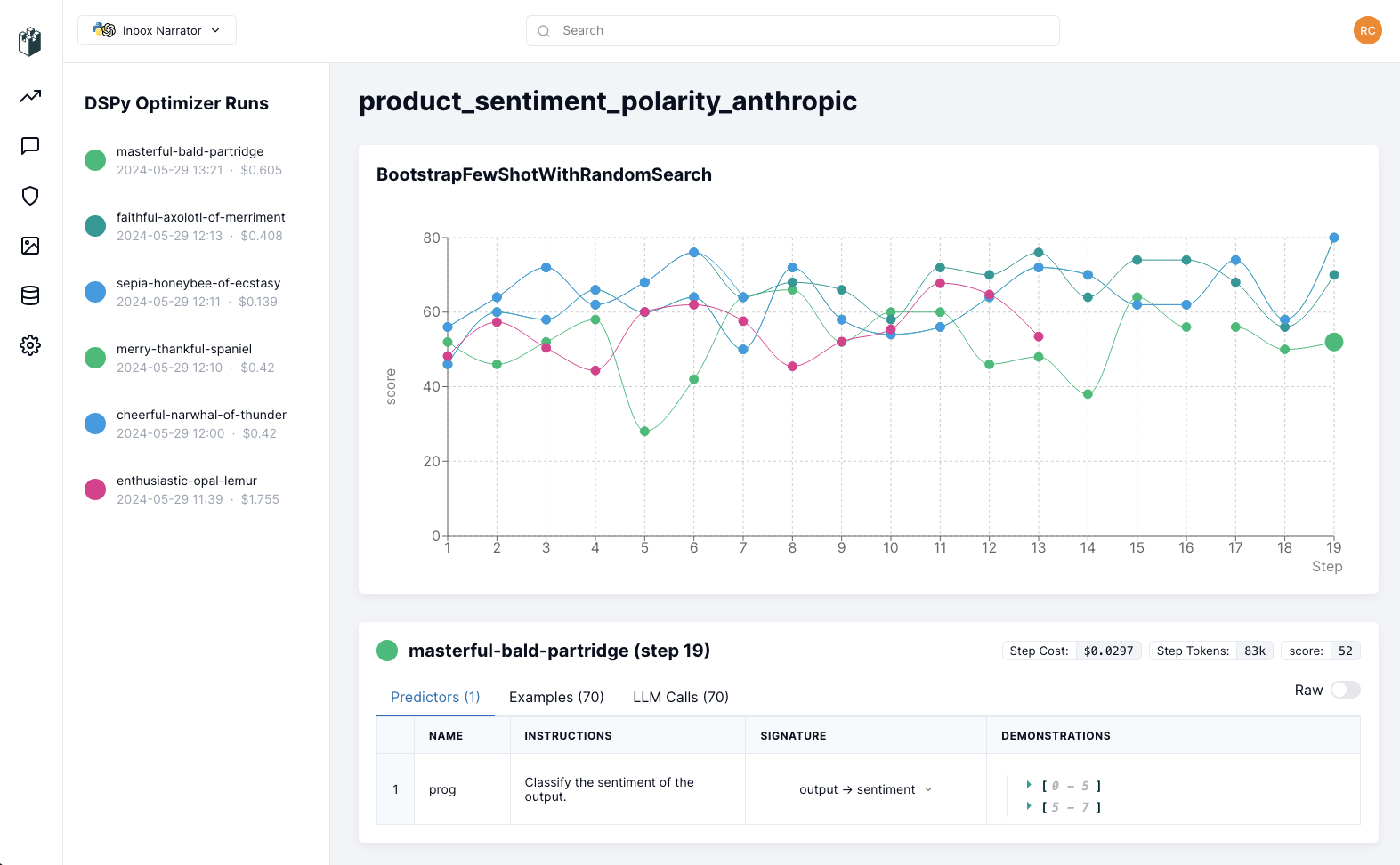
DSPy101
DSPy 介绍 DSPy(Declarative Self-improved Language Programs in Python) 是一个用于系统化和增强在流水线内使用语言模型的框架,它通过数据驱动和意图驱动的系统来优化大型语言模型(LLM)的使用。 DSPy 的核心是模块…...

网格交易策略:从原理、应用到实战Python回测
01 引言 随着金融市场的快速发展,量化交易成为投资者追求收益的一种重要手段。在众多的量化交易策略中,网格交易策略(Grid Trading Strategy)因其简单易用、风险控制灵活等优点而备受青睐。网格交易策略的核心思想是“低买高卖”&…...

软考论文《论大数据处理架构及其应用》精选试读
论文真题 模型驱动架构设计是一种用于应用系统开发的软件设计方法,以模型构造、模型转换和精化为核心,提供了一套软件设计的指导规范。在模型驱动架构环境下,通过创建出机器可读和高度抽象的模型实现对不同问题域的描述,这些模型…...

fatfs API使用手册
配置 /*---------------------------------------------------------------------------/ / Configurations of FatFs Module /---------------------------------------------------------------------------*/#define FFCONF_DEF 80286 /* Revision ID *//*---------------…...

9.23作业
仿照string类,自己手动实现 My_string 代码如下 MyString.h #ifndef MYSTRING_H #define MYSTRING_H #include <iostream> #include <cstring>using namespace std;class My_string { private:char *ptr; //指向字符数组的指针int size; …...

Unity3D 房间去重叠化算法详解
前言 在Unity3D游戏开发中,经常需要生成和处理多个房间的场景,特别是在地牢生成、房屋布局或迷宫设计等应用中。为了确保生成的房间不会重叠,我们需要一种有效的去重叠化算法。以下将详细介绍该算法的原理和代码实现。 对惹,这里有…...

mybatis 配置文件完成增删改查(五) :单条件 动态sql查询,相当于switch
文章目录 单条件 动态sql查询写测试方法 疑问总结 单条件 动态sql查询 <select id"selectByConditionBySingle" resultMap"brandResultMap">.select *from tb_brandwhere<choose>/*相当于switch*/<when test"status ! null">…...

全球IP归属地查询-IP地址查询-IP城市查询-IP地址归属地-IP地址解析-IP位置查询-IP地址查询API接口
IP地址城市版查询接口 API是指能够根据IP地址查询其所在城市等地理位置信息的API接口。这类接口在网络安全、数据分析、广告投放等多个领域有广泛应用。以下是一些可用的IP地址城市版查询接口API及其简要介绍 1. 快证 IP归属地查询API 特点:支持IPv4 提供高精版、…...
)
Vue3+FastAPI中Token的刷新机制(含代码示例)
在Vue3和FastAPI的应用中,token刷新机制通常涉及以下几个步骤: 登录过程:用户登录时,后端FastAPI验证用户信息,验证通过后生成一个访问令牌(access token)和一个刷新令牌(refresh t…...

【GAN 图像生成】
理论知识学习: PART 1: 生成对抗网络GAN 深度学习模型,用于生成数据 对抗式训练,生成器v判别器 DCGAN>WGAN>StyleGAN技术不断进化 GAN在艺术创作。数据增强领域应用越来越广泛 应用: GAN在图像合成&#x…...

【自然语言处理】词嵌入模型
词嵌入(Word Embedding) 是一种将词汇表示为实数向量的技术,通常是低维度的连续向量。这些向量被设计为捕捉词汇之间的语义相似性,使得语义相似的词在嵌入空间中的距离也更近。词嵌入可以看作是将离散的语言符号(如单词…...

了解针对基座大语言模型(类似 ChatGPT 的架构,Decoder-only)的重头预训练和微调训练
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 随着自然语言处理(NLP)技术的飞速进步,基于 Transformer 架构的大语言模型在众多任务中取得了显著成就。特别是 Decoder-only 架构,如 GPT 系列模型&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
