not exist 解决一对多 场景 条件过滤问题
场景:
现在存在一对多关系,蓝色的盒子装的篮球,黄的的盒子装的黄球,
黑色的盒子 (模拟工作类似场景)
| boxId | ballId |
|---|---|
| 蓝盒ID-1 | 5 |
| 蓝盒ID-1 | 6 |
| 蓝盒ID-1 | 7 |
| 黄盒ID-2 | 12 |
| 黄盒ID-2 | 15 |
| 黄盒ID-2 | 16 |
| 黑盒ID-3 | 8 |
| 黑盒ID-3 | 9 |
需求:
例如 6,7,15这三个球为坏球,我现在不想查出这三个球以及他们所属的盒子的数据。
正常的left join where 实现不了这个效果。
select * from boxleft join Ball ON Box.id = Ball.boxIdwhere Ball.boxId not in (6,7,15)
查出的效果:
| boxId | ballId |
|---|---|
| 蓝盒ID-1 | 5 |
| 黄盒ID-2 | 12 |
| 黄盒ID-2 | 16 |
| 黑盒ID-3 | 8 |
| 黑盒ID-3 | 9 |
但其实想要的效果是:
| boxId | ballId |
|---|---|
| 黑盒ID-3 | 8 |
| 黑盒ID-3 | 9 |
因为 6,7都属于蓝盒ID-1这个组,6,7为坏球 ,只要蓝盒ID-1的数据我就要过滤掉
15 同理,属于黄盒ID-2,只要是黄盒ID-2的数据就要过滤掉。
所以 思路就是
先根据目标坏球 查出对应的盒子Id,再根据盒子Id来过滤。
select box.id,* from boxleft join Ball ON Box.id = Ball.boxIdwhere xxxand NOT EXISTS(select t.id from Ball t where t.id in (6,7,15) where t.id = box.id)
当然不用exist 用in也可以实现,这里就是给出了一种解决思路。
相关文章:

not exist 解决一对多 场景 条件过滤问题
场景: 现在存在一对多关系,蓝色的盒子装的篮球,黄的的盒子装的黄球, 黑色的盒子 (模拟工作类似场景) boxIdballId蓝盒ID-15蓝盒ID-16蓝盒ID-17黄盒ID-212黄盒ID-215黄盒ID-216黑盒ID-38黑盒ID-39 需求&a…...

解决$‘r‘ command not found或者文件夹显示’tvsf 33‘$‘r‘
问题现象: 某客户反馈在执行脚本的时候文件夹显示存在问题,如下图: 但是脚本文件中的内容并没有\r字符,如下图: 也有客户反馈如下: 问题分析: $\r’是回车符的转义表示。在Unix和Linux系统中,回车符是一个不可见的控制字符,它通常用于文本文件中的行结尾。以上…...

linux:详解nohup命令
在 UNIX 和类 UNIX 操作系统(如 Linux 和 macOS)中,nohup 意图为后台运行且免疫挂断信号的命令,用于在用户注销(logout)或终端关闭后继续运行相应的进程。 基本语法 启动进程 nohup [COMMAND] [ARG...] …...

负载箱:充电桩测试利器
RCD负载箱是用于测试和验证电气设备在故障状态下的性能的设备。它可以模拟真实的负载情况,从而帮助工程师和技术人员对设备进行准确的检测和维护。此外,RCD负载箱也是一种重要的安全保护设备,主要用于防止电路中的漏电现象引发的事故。它通常…...

Ubuntu 开机自启动 .py / .sh 脚本,可通过脚本启动 roslaunch/roscore等
前言 项目中要求上电自启动定位程序,所以摸索了一种 Ubuntu 系统下开机自启动的方法,开机自启动 .sh 脚本,加载 ROS 环境的同时启动 .py 脚本。在 . py 脚本中启动一系列 ROS 节点。 一、 .sh 脚本的编写 #!/bin/bash # gnome-terminal -- …...

RabbitMQ 消息队列:生产者与消费者实现详解
在分布式系统中,消息队列(Message Queue, MQ)是一种重要的组件,用于解耦系统、异步处理任务以及实现系统间的通信。RabbitMQ 是一个流行的开源消息代理软件,它实现了高级消息队列协议(AMQP)。在…...

vue3项目中组件切换不起作用
以下这种方式写页面中组件切换,不起作用。 <component :is"steps[compIndex].comp" />解决:使用shallowReactive或者shallowRef把对应的组件名称重新定义下。 <component :is"compNames[steps[compIndex].comp]" /> &…...

YOLOv11改进策略【损失函数篇】| Slide Loss,解决简单样本和困难样本之间的不平衡问题
一、本文介绍 本文记录的是改进YOLOv11的损失函数,将其替换成Slide Loss,并详细说明了优化原因,注意事项等。Slide Loss函数可以有效地解决样本不平衡问题,为困难样本赋予更高的权重,使模型在训练过程中更加关注困难样…...

动静态库(Linux)
文章目录 前言一、静态库二、动态库三、深入理解动态库总结 前言 我们之前用过c语言的库.Linux中默认的都是使用动态库,如果想要使用静态库,就必须加上-static选项。默认都是安装的动态库,系统中一般没有静态库,如果要使用&#…...

51单片机和ARM单片机的区别
在嵌入式系统设计与应用中,单片机作为核心控制单元,扮演着至关重要的角色。其中,51单片机和ARM单片机作为两种常见的单片机类型,各自具有独特的特点和优势。本文将从多个维度深入探讨这两种单片机的区别,以便读者更好地…...

[Day 81] 區塊鏈與人工智能的聯動應用:理論、技術與實踐
區塊鏈在食品安全中的應用 前言 食品安全一直是全球關注的問題,隨著全球供應鏈的複雜性增加,追踪食品從生產到消費的過程變得愈發困難。區塊鏈技術以其去中心化、不可篡改的特性,為食品安全提供了可靠的解決方案。在這篇文章中,…...

flac格式怎么转mp3?关于flac转为MP3的方法介绍
flac格式怎么转mp3?MP3格式经过压缩,相较于flac文件,显著减小了文件体积。这一特点使得音乐的存储和传输更加便捷,尤其适合移动设备以及存储空间有限的场景。由于MP3文件体积较小,分享音乐变得非常简单,无论…...

【笔记】KaiOS 系统框架和应用结构(APP界面逻辑)
KaiOS系统框架 最早自下而上分成Gonk-Gecko-Gaia层,代码有同名的目录,现在已经不用这种称呼。 按照官网3.0的版本迭代介绍,2.5->3.0已经将系统更新成如下部分: 仅分为上层web应用和底层平台核心,通过WebAPIs连接上下层,这也是kaios系统升级变更较大的部分。 KaiOS P…...

java项目实现钉钉异常告警实时监控
最近有个小伙伴问我,我们的项目核心业务的地方总是有异常,虽然有打印日志,但不能立马通知我;所以今天我就教大家如何实现异常报警实时提醒 1.需要有钉钉 自己新建的企业用户 2.建一个群,需要有三人以上;…...

Spring Boot应用:电子商务平台开发
第2章 关键技术简介 2.1 Java技术 Java是一种非常常用的编程语言,在全球编程语言排行版上总是前三。在方兴未艾的计算机技术发展历程中,Java的身影无处不在,并且拥有旺盛的生命力。Java的跨平台能力十分强大,只需一次编译…...

怎么在Vue3项目中引入Vant组件库并使用?
文章目录 前言一、项目中使用步骤1.安装:2.样式的导入(2种方法)2.1 main.ts全局导入(平常自己的项目用的这个全局)2.2 按需引入组件样式 (简单介绍一下)1.安装插件2.配置插件 3.组件按需使用:App.vue 总结 …...

springboot中有哪些方式可以解决跨域问题
文章目录 什么是跨域解决方案CrossOrigin注解实现WebMvcConfigurer接口CorsFilter过滤器如何选择? 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 Talk is cheap ࿰…...

Temporal Dynamic Quantization for Diffusion Models阅读
文章目录 AbstractIntroductionBackgrounds and Related Works2.1 扩散模型2.2 量化2.3 量化感知训练和训练后量化 TemporalDynamic Quantization3.1 量化方法3.2 扩散模型量化的挑战3.3 TDQ模块的实现3.4 工程细节时间步的频率编码TDQ模块的初始化 Experimental SetupResults5…...

828华为云征文|华为云Flexus X实例性能实测:速度与稳定性的完美结合
828华为云征文|华为云Flexus X实例性能实测:速度与稳定性的完美结合 前言一、Flexus云服务器X实例介绍1.1 Flexus云服务器X实例简介1.2 Flexus云服务器X实例特点1.3 Flexus云服务器X实例使用场景 二、实践环境介绍2.1 本次实践环境规划2.2 本次实践介绍 …...

【PyTorch】图像分割
图像分割是什么 Image Segmentation 将图像每一个像素分类 图像分割分类 超像素分割:少量超像素代替大量像素,常用于图像预处理语义分割:逐像素分类,无法区分个体实例分割:对个体目标进行分割全景分割:…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...
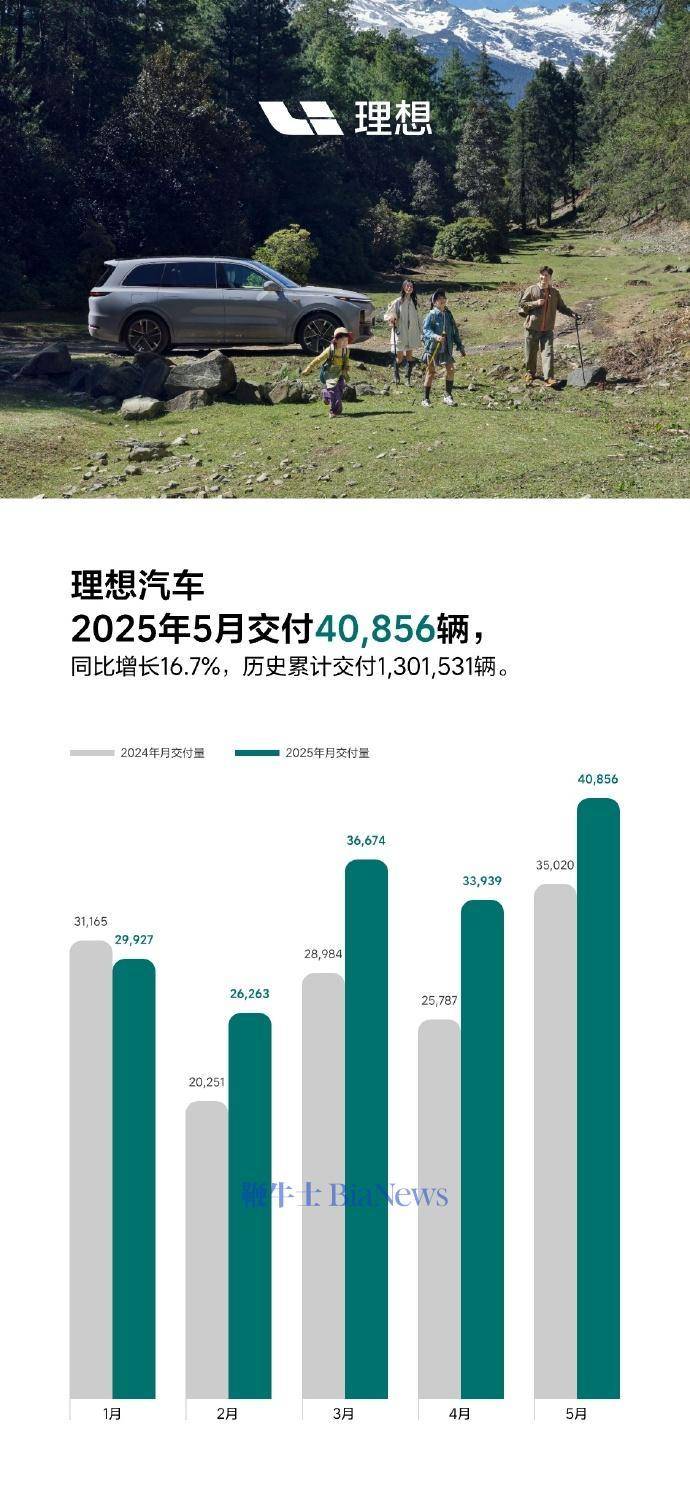
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
