【深度学习基础模型】玻尔兹曼机BM|受限玻尔兹曼机RBM|深度置信网络DBN详细理解并附实现代码。
【深度学习基础模型】玻尔兹曼机Boltzmann machines (BM)|受限玻尔兹曼机Restricted Boltzmann machines (RBM)|深度置信网络Deep belief networks (DBN)详细理解并附实现代码。
【深度学习基础模型】玻尔兹曼机Boltzmann machines (BM)|受限玻尔兹曼机Restricted Boltzmann machines (RBM)|深度置信网络Deep belief networks (DBN)详细理解并附实现代码。
文章目录
- 【深度学习基础模型】玻尔兹曼机Boltzmann machines (BM)|受限玻尔兹曼机Restricted Boltzmann machines (RBM)|深度置信网络Deep belief networks (DBN)详细理解并附实现代码。
- 1. 玻尔兹曼机(Boltzmann Machine, BM)
- 1.1 提出与概述
- 1.2 发展与应用
- 1.3 优缺点
- 1.4 BM的Python实现
- 2. 受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)
- 2.1 提出与概述
- 2.2 发展与应用
- 2.3 优缺点
- 2.4 RBM的Python实现
- 3. 深度信念网络(Deep Belief Network, DBN)
- 3.1 提出与概述
- 3.2 发展与应用
- 3.3 优缺点
- 3.4 DBN的Python实现
- 总结
参考地址:https://www.asimovinstitute.org/neural-network-zoo/
论文地址:
https://ieeexplore.ieee.org/document/6302930
https://ieeexplore.ieee.org/document/6302931?arnumber=6302931
https://ieeexplore.ieee.org/document/6287632
欢迎宝子们点赞、关注、收藏!欢迎宝子们批评指正!
1. 玻尔兹曼机(Boltzmann Machine, BM)
1.1 提出与概述
玻尔兹曼机(BM)是一种随机生成模型,由Geoffrey Hinton等人在20世纪80年代提出。BM的主要特点是它具有双向连接的无向图结构,每个神经元的状态受到与其连接的其他神经元的状态和权重影响。BM通过最小化能量函数,使网络达到稳定状态,并可以用于无监督学习。BM中包含输入神经元和隐藏神经元,输入神经元在每次网络更新后可以成为输出神经元。
BM是一种随机网络,神经元主要采用二进制激活模式(0或1),通过马尔可夫链蒙特卡洛方法(MC)进行训练。训练过程中,BM反复在输入和隐藏神经元之间交换信息,直到网络达到平衡状态。
1.2 发展与应用
BM虽然具有强大的表达能力,但由于全连接结构的存在,导致训练复杂度极高。在实际应用中,BM常用于学习复杂的概率分布和生成新数据。然而,随着BM训练的难度逐渐显现,人们更倾向于使用RBM等改进模型。BM适合用于需要学习数据分布或生成数据的领域,但由于其高计算开销,较少在现代大规模应用中使用。
1.3 优缺点
优点:
- 能够学习复杂的概率分布并生成新数据。
- 提供了概率解释,使得模型在统计物理学中有坚实的理论基础。
缺点:
- 由于全连接结构,BM的计算复杂度极高,训练过程缓慢。
- 训练时容易陷入局部最优,难以扩展到大规模数据集。
1.4 BM的Python实现
import numpy as npclass BM:def __init__(self, n_visible, n_hidden):self.n_visible = n_visibleself.n_hidden = n_hiddenself.weights = np.random.randn(n_visible, n_hidden)self.visible_bias = np.zeros(n_visible)self.hidden_bias = np.zeros(n_hidden)def energy(self, visible, hidden):return -np.dot(visible, np.dot(self.weights, hidden)) - np.dot(self.visible_bias, visible) - np.dot(self.hidden_bias, hidden)def train(self, data, epochs=1000):for epoch in range(epochs):# 简单的伪马尔可夫链蒙特卡洛训练过程visible = data[np.random.randint(0, len(data))]hidden = np.dot(visible, self.weights) + self.hidden_biasvisible_recon = np.dot(hidden, self.weights.T) + self.visible_bias# 这里省略了具体的梯度更新逻辑print("BM训练完成")data = np.array([[0, 1, 1, 0], [1, 0, 1, 1], [1, 1, 0, 0]])
bm = BM(n_visible=4, n_hidden=2)
bm.train(data)
代码解释:
energy: 能量函数用于计算系统的能量状态。train: 简化版本的BM训练过程,通过随机初始化数据和简单的矩阵操作来模拟BM的训练。
2. 受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)
2.1 提出与概述
RBM是BM的简化版本,由Hinton提出。与BM的全连接结构不同,RBM对连接方式进行了限制:输入层神经元之间没有连接,隐藏层神经元之间也没有连接。这种限制大大降低了训练的复杂度,RBM通过对比散度算法(Contrastive Divergence, CD)进行训练,逐步成为一种有效的无监督学习模型。
2.2 发展与应用
RBM广泛应用于降维、特征提取、推荐系统等领域。它是深度信念网络(DBN)的基本单元,并且常用于无监督预训练阶段。
2.3 优缺点
优点:
- RBM的结构限制降低了计算复杂度,提高了训练效率。
- 可以用于特征提取、降维等任务,并且能作为深度学习的预训练步骤。
- 能够通过堆叠多个RBM,构建深度学习模型(如DBN)。
缺点:
- 尽管RBM比BM高效,但训练过程中仍然依赖马尔可夫链,存在近似误差。
- 在大规模数据集上应用时,仍需大量计算资源。
2.4 RBM的Python实现
import numpy as npclass RBM:def __init__(self, n_visible, n_hidden, learning_rate=0.1):self.n_visible = n_visibleself.n_hidden = n_hiddenself.learning_rate = learning_rateself.weights = np.random.randn(n_visible, n_hidden) * 0.01self.visible_bias = np.zeros(n_visible)self.hidden_bias = np.zeros(n_hidden)def sigmoid(self, x):return 1.0 / (1 + np.exp(-x))def sample_hidden(self, visible_states):hidden_activations = np.dot(visible_states, self.weights) + self.hidden_biashidden_probs = self.sigmoid(hidden_activations)return hidden_probsdef train(self, data, epochs=1000):for epoch in range(epochs):for sample in data:hidden_probs = self.sample_hidden(sample)positive_grad = np.outer(sample, hidden_probs)visible_recon = self.sigmoid(np.dot(hidden_probs, self.weights.T) + self.visible_bias)hidden_recon = self.sample_hidden(visible_recon)negative_grad = np.outer(visible_recon, hidden_recon)self.weights += self.learning_rate * (positive_grad - negative_grad)self.visible_bias += self.learning_rate * (sample - visible_recon)self.hidden_bias += self.learning_rate * (hidden_probs - hidden_recon)print("RBM训练完成")data = np.array([[0, 1, 1], [1, 0, 1], [1, 1, 0]])
rbm = RBM(n_visible=3, n_hidden=2)
rbm.train(data)
代码解释:
sample_hidden: 从可见层推导出隐藏层的激活概率。train: 利用对比散度算法进行权重更新,正向传播与反向重建数据,调整模型参数。
3. 深度信念网络(Deep Belief Network, DBN)
3.1 提出与概述
DBN是由多个RBM堆叠而成的深度学习模型,Hinton于2006年提出。DBN通过贪婪逐层训练,每个RBM只需学习前一层的特征表示。DBN的目的是通过多个RBM的逐步预训练,将复杂数据表示为概率模型。
3.2 发展与应用
DBN常用于图像识别、语音识别等复杂任务中,尤其在无监督学习和半监督学习中表现突出。DBN的预训练可以有效解决梯度消失问题,并为后续的监督学习提供良好的初始权重。
3.3 优缺点
优点:
- DBN可以有效解决深层神经网络中的梯度消失问题,尤其在无监督预训练时表现优异。
- 能够从数据中学习复杂的概率表示,用于生成模型、分类等任务。
- 通过RBM层堆叠,DBN在图像识别、语音识别等领域表现出色。
缺点:
- 训练时间较长,特别是在层数较多时,调优变得复杂。
- 预训练和反向传播结合的训练方式增加了模型的复杂性。
3.4 DBN的Python实现
class DBN:def __init__(self, layer_sizes):self.rbms = [RBM(layer_sizes[i], layer_sizes[i+1]) for i in range(len(layer_sizes) - 1)]def pretrain(self, data, epochs=1000):input_data = datafor rbm in self.rbms:rbm.train(input_data, epochs=epochs)input_data = rbm.sample_hidden(input_data)def fine_tune(self, data, labels, epochs=1000):# 细调阶段可以使用反向传播算法pass# 创建一个DBN,包含3个RBM层
dbn = DBN([3, 4, 2])
data = np.array([[0, 1, 1], [1, 0, 1], [1, 1, 0]])
dbn.pretrain(data, epochs=1000)
代码解释:
DBN: 初始化DBN时会创建多个RBM层。pretrain: 使用贪婪的逐层预训练,每个RBM层分别学习前一层的表示。
总结

- BM 是最原始的玻尔兹曼机,理论上强大但实际应用受限于其高计算复杂度。
- RBM 通过限制连接结构大大提高了效率,适合用于无监督学习任务,尤其是特征提取和预训练。
- DBN 通过堆叠多个RBM,构建了强大的深度学习架构,适合处理复杂的高维数据,并解决了深层神经网络中的梯度消失问题。
这些模型在深度学习的发展中起到了重要的奠基作用,尽管现在更为流行的技术(如深度卷积网络、生成对抗网络等)已经取代了它们,但它们在无监督学习领域的贡献仍然不可忽视。
相关文章:

【深度学习基础模型】玻尔兹曼机BM|受限玻尔兹曼机RBM|深度置信网络DBN详细理解并附实现代码。
【深度学习基础模型】玻尔兹曼机Boltzmann machines (BM)|受限玻尔兹曼机Restricted Boltzmann machines (RBM)|深度置信网络Deep belief networks (DBN)详细理解并附实现代码。 【深度学习基础模型】玻尔兹曼机Boltzmann machines (BM)|受限玻尔兹曼机Restricted Boltzmann m…...

滑动窗口->dd爱框框
1.题目: 2.题解: 2.1为什么用滑动窗口优化: 因为元素都是大于0的 所以:当找到大于等于x的值时,right可以不用返回 两个指针都往后走;因此可以使用滑动窗口优化暴力解法 2.2:滑动窗口具体使用步…...
Python从入门到高手4.1节-掌握条件控制语句
目录 4.1.1 理解条件控制 4.1.2 if, elif, else 4.1.3 条件表达式 4.1.4 条件控制可以嵌套 4.1.5 if语句的三元运算 4.1.6 国庆节快乐 4.1.1 理解条件控制 在日常生活中,我们常喜欢说如果, "如果怎么样,那么就会怎么样"。"如果&qu…...

使用Qt实现实时数据动态绘制的折线图示例
基于Qt的 QChartView 和定时器来动态绘制折线图。它通过动画的方式逐步将数据点添加到图表上,并动态更新坐标轴的范围,提供了一个可以实时更新数据的折线图应用。以下是对代码的详细介绍及其功能解析: 代码概述 该程序使用Qt的 QChartView…...

【人人保-注册安全分析报告-无验证方式导致安全隐患】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 1. 暴力破解密码,造成用户信息泄露 2. 短信盗刷的安全问题,影响业务及导致用户投诉 3. 带来经济损失,尤其是后付费客户,风险巨大,造…...

Redis6 多线程模型
优质博文:IT-BLOG-CN 一、单线程的优缺点 对于一个请求操作Redis主要做3件事情:从客户端读取数据/解析、执行Redis命令、回写数据给客户端。所以主线程其实就是把所有操作的这3件事情串行一起执行,因为是基于内存,所以执行速度非…...

Python的异步编程
什么是协程? 协程不是计算机系统提供,程序员人为创造。 协程也可以被称为微线程,是一种用户态内的上下文切换技术。简而言之,其实就是通过一个线程实现代码块相互切换执行。 实现协程有那么几种方法: greenlet&…...

初识Linux · 进程等待
目录 前言: 进程等待是什么 为什么需要进程等待 进程等待都在做什么 前言: 通过上文的学习,我们了解了进程终止,知道终止是在干什么,终止的三种情况,以及有了退出码,错误码的概念ÿ…...

面向对象建模
UML 关系 UML 关系主要有:依赖、关联、聚合、组合、实现、继承。 类图 #mermaid-svg-jcAjcVcPmgmWDpcI {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-jcAjcVcPmgmWDpcI .error-icon{fill:#552222;}#m…...

MetaJUI v0.4 遇到的一些问题及解决办法记录
1、Unity3d 版本 2022.3.29f1。 2、MetaJUI v0.4 的下载,https://download.csdn.net/download/xingchengaiwei/89334848 3、将MetaJUI v0.4解压,用Unity3d 打开项目,会出现如下问题,按照图中提示操作即可。 4、打开工程后会出现…...

从零开始学习OMNeT++系列第二弹——新建一个OMNeT++的工程
上一篇第一弹介绍了OMNeT是什么以及如何安装OMNeT,现在来说一下如何新建一个自己的OMNeT的工程。 在 Omnet安装完成后,samples/tictoc 中有该例子的完整文件,你可以立刻运行该文件看他是怎么工作的,不过更推荐按接下来的步骤一步…...
【Android】布局优化—include,merge,ViewStub的使用方法
引言 1.重要性 在Android应用开发中,布局是用户界面的基础。一个高效的布局不仅能提升用户体验,还能显著改善应用的性能。随着应用功能的复杂性增加,布局的优化变得尤为重要。优化布局能够减少渲染时间,提高响应速度,…...

传奇外网架设教程带图文解说—Gee引擎
架设前准备工作: ①通过百度网盘下载版本、补丁、客户端和DBC2000。版本解压到D盘,客户端解压到D盘或是E盘,补丁先不解压 ②安装和配置DBC2000,有些版本不一定用的是DBC2000数据库,看引擎默认的数据库是哪个 DBC数据…...

MySQL | excel数据输出insert语句
需求 在日常生产运维过程中,有很多需要进行人工梳理的excel数据,到了研发这一侧需要转为sql语句进行数据修正,如何输出insert插入语句? 方案 在空白列插入,选择需要的列 "INSERT INTO tab_name1 (name, desc) …...

足球青训俱乐部管理:Spring Boot技术驱动
摘 要 随着社会经济的快速发展,人们对足球俱乐部的需求日益增加,加快了足球健身俱乐部的发展,足球俱乐部管理工作日益繁忙,传统的管理方式已经无法满足足球俱乐部管理需求,因此,为了提高足球俱乐部管理效率…...

一次实践:给自己的手机摄像头进行相机标定
文章目录 1. 问题引入2. 准备工作2.1 标定场2.2 相机拍摄 3. 基本原理3.1 成像原理3.2 畸变校正 4. 标定解算4.1 代码实现4.2 详细解析4.2.1 解算实现4.2.2 提取点位 4.3 解算结果 5. 问题补充 1. 问题引入 不得不说,现在的计算机视觉技术已经发展到足够成熟的阶段…...

【docker学习】Linux系统离线方式安装docker环境方法
centos7-linux安装docker(离线方式) 下载docker的安装文件 https://download.docker.com/linux/static/stable/x86_64/ 下载的是:docker-18.06.3-ce.tgz 这个压缩文件 将docker-18.06.3-ce.tgz文件上传到centos7-linux系统上,用ftp工具上传即可 解压…...

vscode开发uniapp安装插件指南
安装vuets的相关插件 首先是vue的相关插件,目前2024年9月应该是vue-offical 安装uniapp开发插件 uni-create-view :快速创建 uni-app 页面 安装uni-create-view之后修改插件拓展设置 勾选第一个选择创建视图时创建同名文件夹 选择第二个创建文件夹中生…...
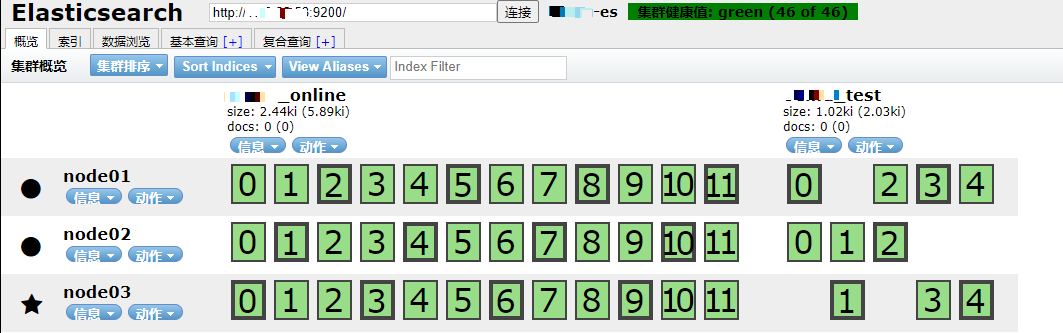
Elasticsearch7.7.1集群不能相互发现的问题解决以及Elasticsearch7.7.1安装analysis-ik中文分词插件的应用
一、Elasticsearch7.7.1集群不能相互发现的问题解决 在使用elasticsearch7.7.1搭建集群,使用了3台服务器作为节点,但在搭建的过程中发现每台服务器的elasticsearch服务都正常,但是不能相互发现,期间进行了一些配置的修改偶尔出现了…...

蓝牙Mesh介绍
蓝牙Mesh(Bluetooth Mesh)是一种基于蓝牙技术的无线通信网络拓扑,用于在设备之间创建大规模的多点到多点网络。蓝牙Mesh网络可以让多个蓝牙设备相互通信和协作,适合需要高覆盖范围和高可靠性的场景,例如智能家居、工业…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
