最大正方形 Python题解
最大正方形
题目描述
在一个 n × m n\times m n×m 的只包含 0 0 0 和 1 1 1 的矩阵里找出一个不包含 0 0 0 的最大正方形,输出边长。
输入格式
输入文件第一行为两个整数 n , m ( 1 ≤ n , m ≤ 100 ) n,m(1\leq n,m\leq 100) n,m(1≤n,m≤100),接下来 n n n 行,每行 m m m 个数字,用空格隔开, 0 0 0 或 1 1 1。
输出格式
一个整数,最大正方形的边长。
样例 #1
样例输入 #1
4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1
样例输出 #1
2
题解
这道题AcWing、洛谷和leetCode都有,只是输入还有输出的些微区别,这里只提供洛谷的Python代码,思路是一样的。
这道题其实不难看出来可以用动态规划做,但是我做这道题的时候是有人要求我先用前缀和做一遍了,所以我这里提供两种思路
1、前缀和
这道题前缀和做法其实很简单,就是看我们想要通过求的正方形的前缀和来求该正方形的面积,如果求出来的面积与正方形边长平方相等,那么这个边长的正方形就满足要求
if 通过前缀和求的面积 == 正方形边长 ** 2:return True

怎么通过前缀和求矩形面积呢?我们可以通过下面公式来计算:
设 i 2 , j 2 i_2, j_2 i2,j2 为矩形右下角, i 1 , j 1 = i 2 − l e n S q u a r e + 1 , j 2 − l e n S q u a r e + 1 i_1, j_1 = i_2 - lenSquare + 1, j_2 - lenSquare + 1 i1,j1=i2−lenSquare+1,j2−lenSquare+1 为矩形左上角,那么通过前缀和求矩形面积公式为:
S i z e ( S q u a r e ) = P r e f i x [ i 2 ] [ j 2 ] − P r e f i x [ i 1 − 1 ] [ j 2 ] − P r e f i x [ i 2 ] [ j 1 − 1 ] + P r e f i x [ i 1 − 1 ] [ j 1 − 1 ] Size(Square) =Prefix[i_2][j_2] -Prefix[i_1-1][j_2]-Prefix[i_2][j_1-1] +Prefix[i_1-1][j_1-1] Size(Square)=Prefix[i2][j2]−Prefix[i1−1][j2]−Prefix[i2][j1−1]+Prefix[i1−1][j1−1]
下面这张图为上图的前缀和矩阵:

那么穷举求出每种正方形边长的情况,我们就可以得到可能的正方形边长
欸,别急,直接穷举正方形边长还是慢了,正方形边长是从小到大穷举的,我们可以使用二分来加速对边长的举证:
if mid正方边长满足要求:我们去找是否存在更大的边长满足要求:left = mid + 1
else:mid长度都不符合要求的,直接去找更小的边长了: right = mid - 1
最后得出Python代码(时间复杂度为 O ( N 2 l o g 2 N ) O(N^2log_2N) O(N2log2N)):
def judge(lenEdge, Prefix):global N, Mfor i in range(lenEdge, N+1):for j in range(lenEdge, M+1):if Prefix[i][j] - Prefix[i-lenEdge][j] - Prefix[i][j-lenEdge] + Prefix[i-lenEdge][j-lenEdge] == lenEdge**2:return Trueelse:return FalseN, M = map(int, input().strip().split())
A = [[0 for _ in range(M+1)]]
for i in range(1, N+1):tmp = [0]tmp.extend(map(int, input().strip().split()))A.append(tmp)
Prefix = [[0 for _ in range(M+1)] for _ in range(N+1)]
for i in range(1, N+1):for j in range(1, M+1):Prefix[i][j] = Prefix[i-1][j] + Prefix[i][j-1] - Prefix[i-1][j-1] + A[i][j]
left, right = 0, min(N, M)
ans = 0
while left <= right:mid = (left + right) // 2if judge(mid, Prefix):ans = max(ans, mid)left = mid + 1else:right = mid - 1
print(ans)

2、动态规划法
动态规划法的想法更容易想到,这里用图来说明一下:

定义 i , j i,j i,j为正方形的左下角坐标,且 d p [ i ] [ j ] dp[i][j] dp[i][j]存的是该正方形的边长
( 4 , 4 ) (4,4) (4,4)代表的正方形的边长可以从红色、蓝色、绿色,( ( 3 , 3 ) , ( 3 , 4 ) , ( 4 , 3 ) (3,3),(3,4),(4,3) (3,3),(3,4),(4,3))三种颜色的正方形来得出,
可以看出来,黑色框出正方形边长为1+1 = 2,通过多画图推导,得出下面的公式:
d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j − 1 ] ) + 1 dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) + 1 dp[i][j]=min(dp[i−1][j],dp[i][j−1],dp[i−1][j−1])+1
时间复杂度为 O ( N 2 ) O(N^2) O(N2)
N, M = map(int, input().strip().split())
A = [[0 for _ in range(M)]] + [[0] + list(map(int, input().strip().split())) for _ in range(N)]
dp = [[0 for _ in range(M+1)] for _ in range(N+1)]
ans = 0
for i in range(1, N+1):for j in range(1, M+1):if A[i][j] == 1:dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1ans = max(ans, dp[i][j])
print(ans)

相关文章:

最大正方形 Python题解
最大正方形 题目描述 在一个 n m n\times m nm 的只包含 0 0 0 和 1 1 1 的矩阵里找出一个不包含 0 0 0 的最大正方形,输出边长。 输入格式 输入文件第一行为两个整数 n , m ( 1 ≤ n , m ≤ 100 ) n,m(1\leq n,m\leq 100) n,m(1≤n,m≤100),接…...

ubuntu中软件的进程管理-结束软件运行
在Ubuntu系统中,当某个运行中的软件无法正常退出时,可以通过以下几种方法强制结束该软件: 方法一:使用系统监视器(System Monitor)–小白专属 这个相当于win上的资源管理器 打开系统监视器 可以通过点击屏…...

Windows环境部署Oracle 11g
Windows环境部署Oracle 11g 1.安装包下载2. 解压安装包3. 数据库安装3.1 执行安装脚本3.2 电子邮件设置3.3 配置安装选项3.4 配置系统类3.5 选择数据库安装类型3.6 选择安装类型3.7 数据库配置3.8 确认安装信息3.9 设置口令 Oracle常用命令 2023年10月中旬就弄出大致的文章&…...

C语言进阶【8】--联合体和枚举(联合体和枚举这么好用,你不想了解一下吗?)
本章概述 联合体类型的声明联合体的特点联合体的大小的计算枚举类型的声明枚举类型的优点枚举类型的使用枚举类型的大小彩蛋时刻!!! 联合体类型的声明 概述:联合体的关键字为 union。它的结构和结构体是一样的。进行展示…...

Android OTA升级
针对Android系统OTA升级,MTK平台有相关介绍文档:https://online.mediatek.com/apps/faq/detail?faqidFAQ27117&listSW 概念一:OTA包的构建 AOSP full build:Android原生提供的全量包的构建,意思就是可以从任何一…...
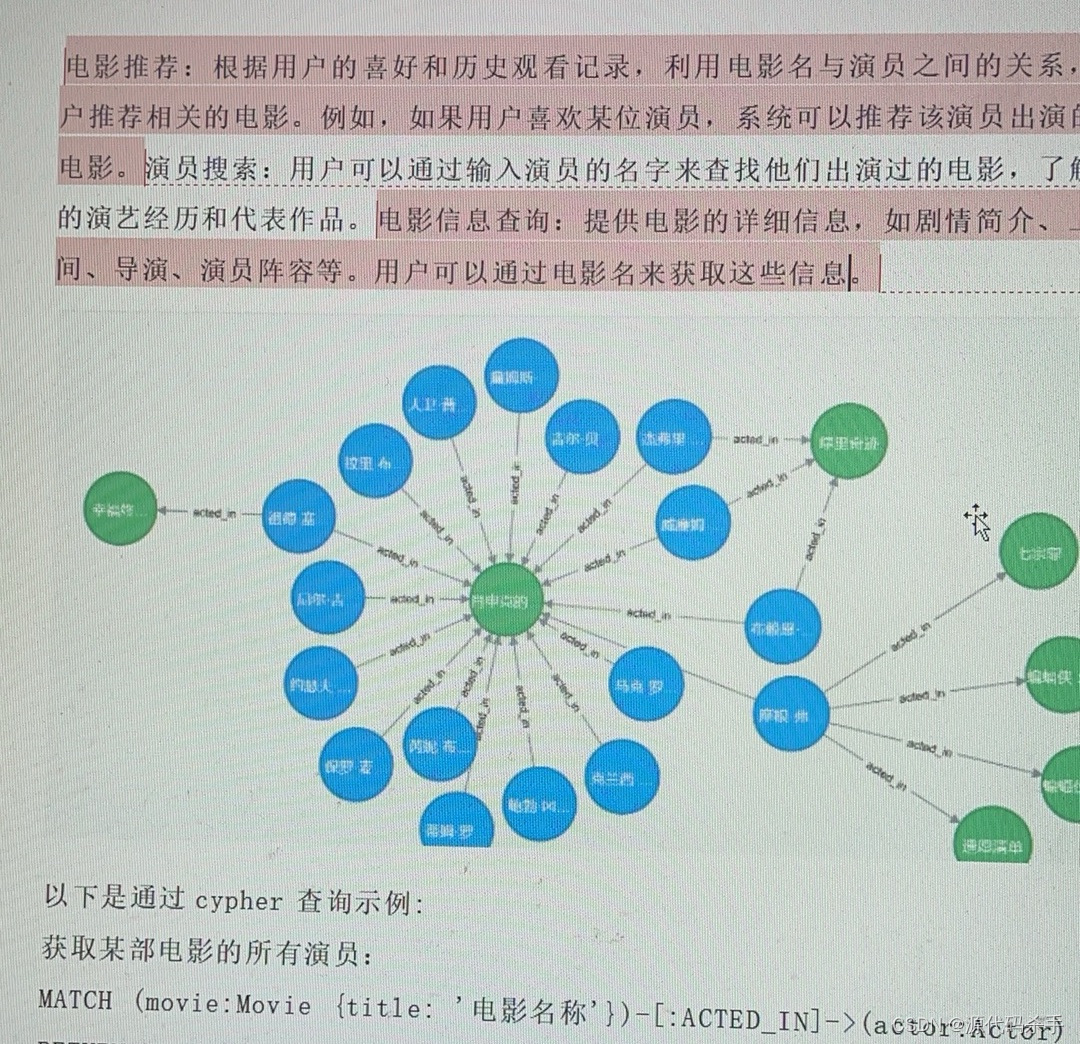
【项目经验分享】深度学习自然语言处理技术毕业设计项目案例定制
以下毕业设计是与深度学习自然语言处理(NLP)相关的毕业设计项目案例,涵盖文本分类、生成式模型、语义理解、机器翻译、对话系统、情感分析等多个领域: 实现案例截图: 基于深度学习的文本分类系统基于BERT的情感分析系…...

一觉醒来,YOLO11 冷不丁就来了
🥇 版权: 本文由【墨理学AI】原创首发、各位读者大大、敬请查阅、感谢三连 🎉 声明: 作为全网 AI 领域 干货最多的博主之一,❤️ 不负光阴不负卿 ❤️ 文章目录 前言:一觉醒来,YOLO11 冷不丁就来了ultralytics 版本更新…...

智能编辑器、版本控制与自动化脚本
在繁忙的工作中,每个开发者都渴望拥有一个“秘密武器”,帮助自己提升效率、减少错误,从而更快地完成任务。那么,在众多编程工具中,哪一款能够成为你的工作效率翻倍的“秘密武器”呢?本文将探讨智能的代码编…...

jenkinsfile实现镜像构建、发布
实现代码打包编译 容器镜像构建 jenkins编译采用docker构建。 遇到问题: 1.需要限制docker 容器的内存和cpu docker { image ‘ccr.ccs.tencentyun.com/libary/maven:3.6.3-jdk-8’ args “-v ${WORKSPACE}:/workspace --memory‘2048m’ --cpus‘1’” } 2.jenkins构建需要限制…...

OSPF路由计算
关于OSPF路由的基础概述可以看看这篇博客 动态路由---OSPF协议基础https://blog.csdn.net/ZZZCY2003/article/details/141335261 区域内路由计算 LSA概述 LSA是OSPF进行路由计算的关键依据OSPF的LSU报文可以携带多种不同类型的LSA各种类型的LSA拥有相同的报文头部 重要字段解…...

【设计模式-迭代】
定义 迭代器模式(Iterator Pattern)是一种行为型设计模式,用于提供一种顺序访问集合对象元素的方式,而不暴露该对象的内部表示。通过迭代器,客户端可以在不需要了解集合实现的细节的情况下遍历集合中的元素。 UML图 …...
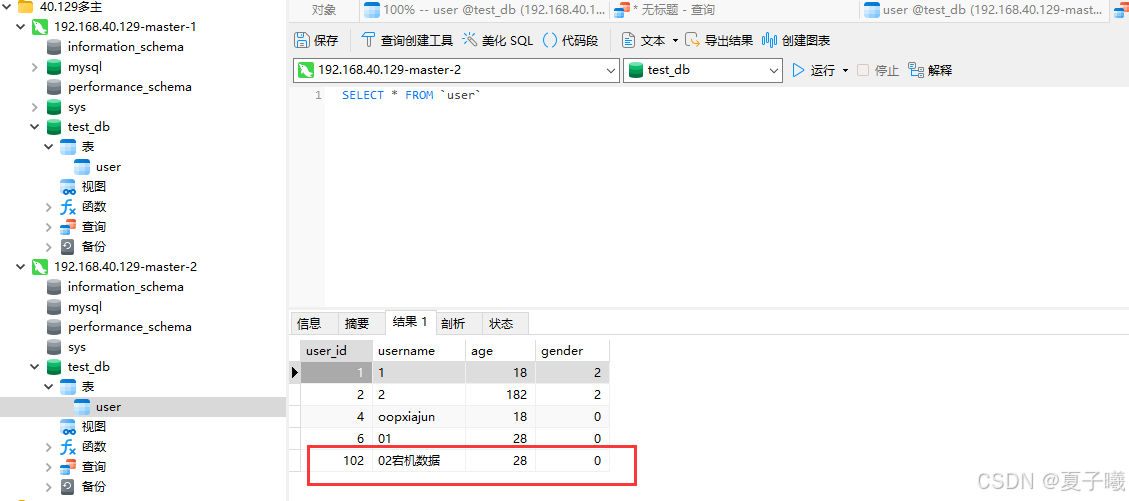
k8s搭建双主的mysql8集群---无坑
《k8s搭建一主三从的mysql8集群---无坑-CSDN博客》通过搭建一主三从,我们能理解到主节点只有1个,那么承担增删改主要还是主节点,如果你在从节点上去操作增删改操作,数据不会同步到其他节点。本章我们将实现多主(双主&a…...

Iterm2配置主题和Oh-My-Zsh
文章目录 一、配置主题1.1 安装使用git1.2 安装手册1.2.1 激活使用主题 二、配置oh-my-zsh2.1、oh-my-zsh插件2.2、oh-my-zsh主题 [Zsh](http://zsh.org/)2.2.1、Install using Git2.2.2、Install manually2.2.3、Activating theme2.2.4、Install using [zplug](https://github…...

html+css+js实现step进度条效果
实现效果 代码实现 HTML部分 <div class"box"><ul class"step"><li class"circle actives ">1</li><li class"circle">2</li><li class"circle">3</li><li class&quo…...
视频采集类VideoCapture之从视频源中读取一帧图像函数read()的使用)
OpenCV视频I/O(8)视频采集类VideoCapture之从视频源中读取一帧图像函数read()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 抓取、解码并返回下一个视频帧。 cv::VideoCapture::read() 是 VideoCapture 类的一个成员函数,用于从视频源中读取一帧图像. 该方法…...

深度学习500问——Chapter17:模型压缩及移动端部署(2)
文章目录 17.4.6 低秩分解 17.4.7 总体压缩效果评价指标有哪些 17.4.8 几种轻量化网络结构对比 17.4.9 网络压缩未来研究方向有哪些 17.5 目前有哪些深度学习模型优化加速方法 17.5.1 模型优化加速方法 17.5.2 TensorRT加速原理 17.5.3 TensorRT如何优化重构模型 17.5.4 Tensor…...

【C#】DllImport的使用
DllImport 是 C# 中用于从非托管 DLL(动态链接库)中导入函数的一个特性。这个特性允许你在 .NET 应用程序中调用由其他语言编写的函数,如 C 或 C。使用 DllImport 可以让你重用现有的非托管代码,而不需要重新实现这些功能。 下面…...

基于 Redis 实现滑动窗口的限流
⏳ 限流场景:突发流量,恶意流量,业务本身需要 基于 Redis 实现滑动窗口的限流是一种常见且高效的做法。Redis 是一种内存数据库,具有高性能和支持原子操作的特点,非常适合用来实现限流功能。下面是一个使用 Redis 实现…...

Camera Raw:打开图像
在图像工作流程中,无论是 Raw 格式图像文件还是 JPEG、TIFF 文件,都可以先使用 Camera Raw 打开并调整后,再进入其它 Adobe 软件如 Photoshop 中进行进一步的编辑和处理。 一、打开 Raw 格式图像 1、通过 Adobe Bridge 打开 在 Adobe Bridge …...

RK3588主板PCB设计学习(六)
可以在其它层对过孔进行削盘处理, 可以看到,这里有些过孔用不上,在这一层进行了削盘处理: 对于这种电源层进行铺铜操作的时候,如果不进行削盘处理的话这些焊盘可能导致这个电源层面不完整,存在割裂的风险&a…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
