【YashanDB知识库】如何配置jdbc驱动使getDatabaseProductName()返回Oracle

本文转自YashanDB官网，具体内容请见https://www.yashandb.com/newsinfo/7352676.html?templateId=1718516

问题现象

某些三方件，例如 工作流引擎activiti，暂未适配yashandb，使用中会出现如下异常：

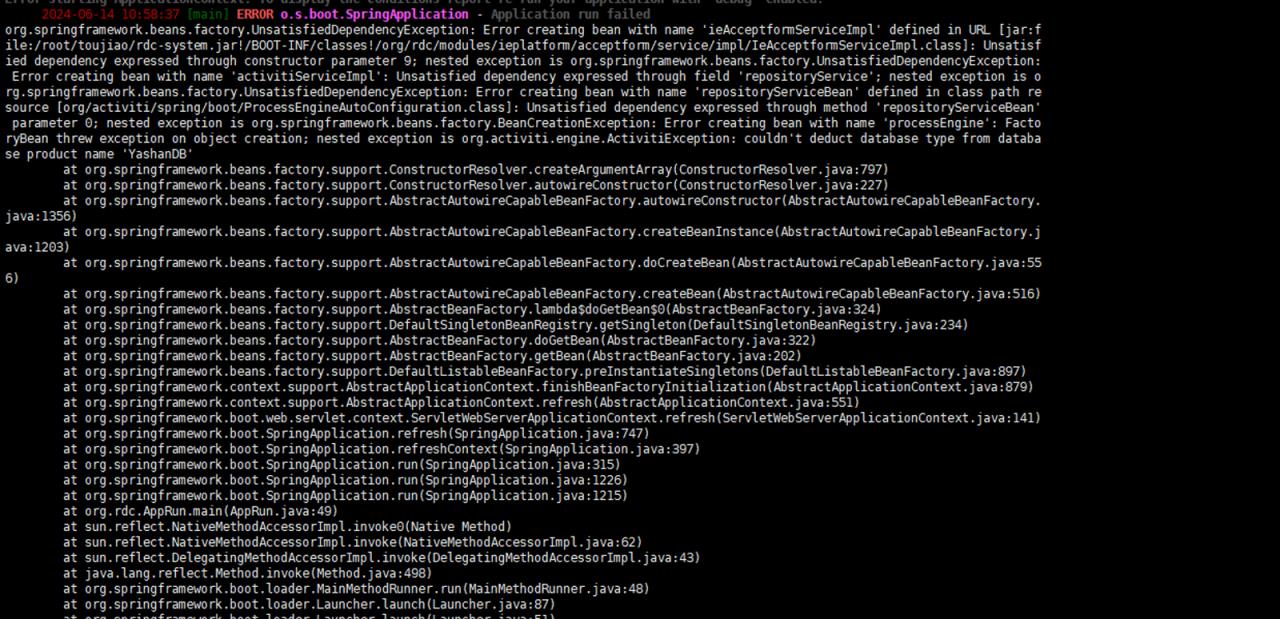
问题的风险及影响

影响客户业务无法进行。

问题影响的版本

所有的yashandb jdbc驱动版本。

问题发生原因

工作流引擎activiti在启动时，会检测数据库厂商。其目前并未适配yashandb，故不认识yashandb

conn.getMetaData().getDatabaseProductName()方法返回的YashanDB，进而抛出异常退出。

解决方法及规避方式

yashandb jdbc 1.7.1及以后版本在连接串中提供了productName选项，可以指定为Oracle(activiti是支持oracle的）。

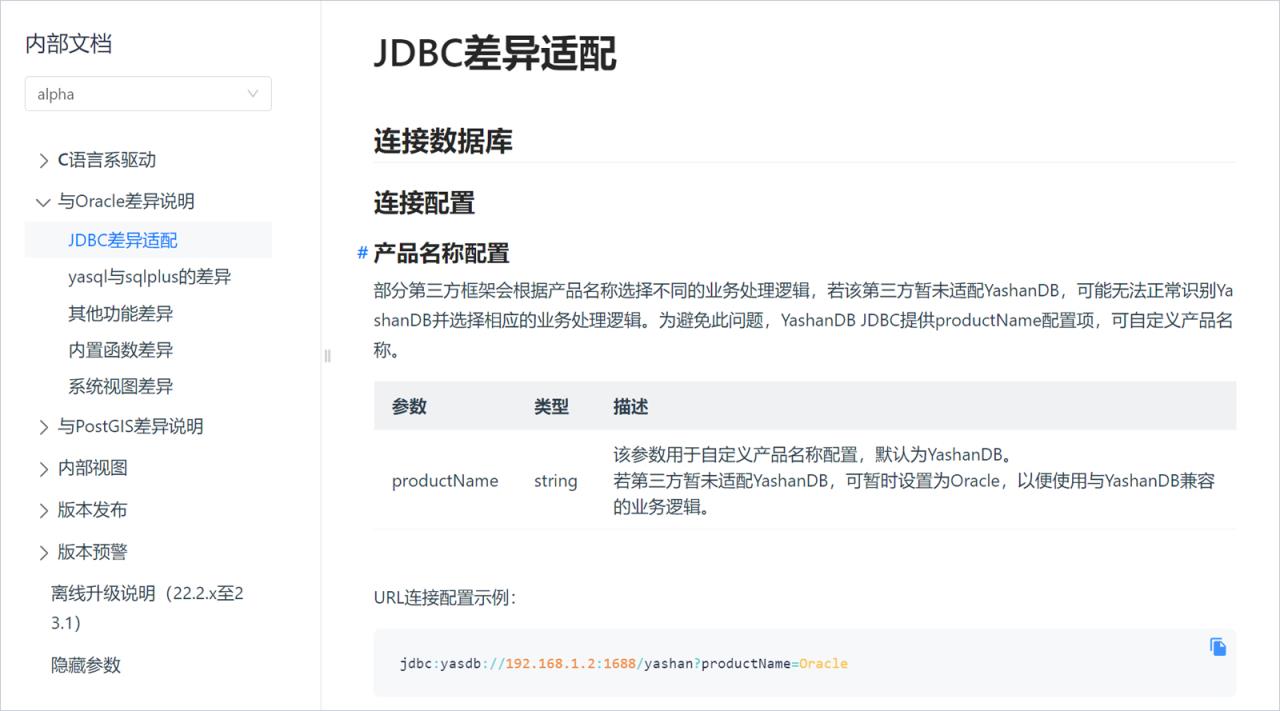
问题分析和处理过程

activiti在启动时会进行databaseProductName的判断，如果不匹配会异常退出：

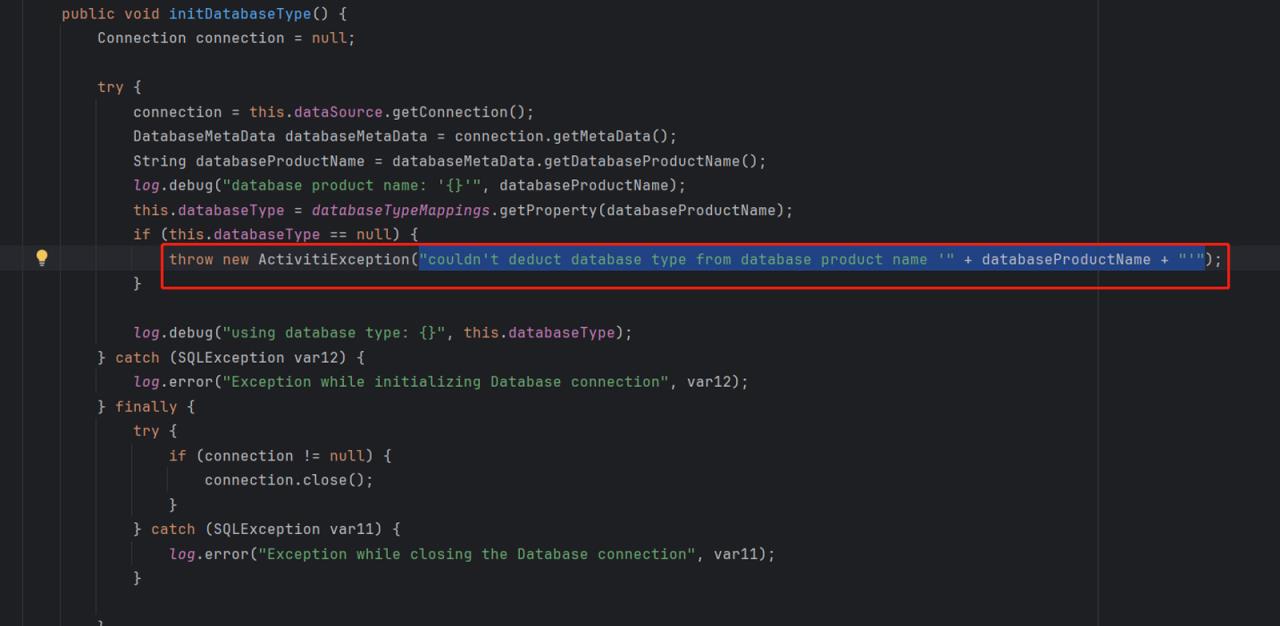
上面截图中的databaseTypeMappings初始化如下：

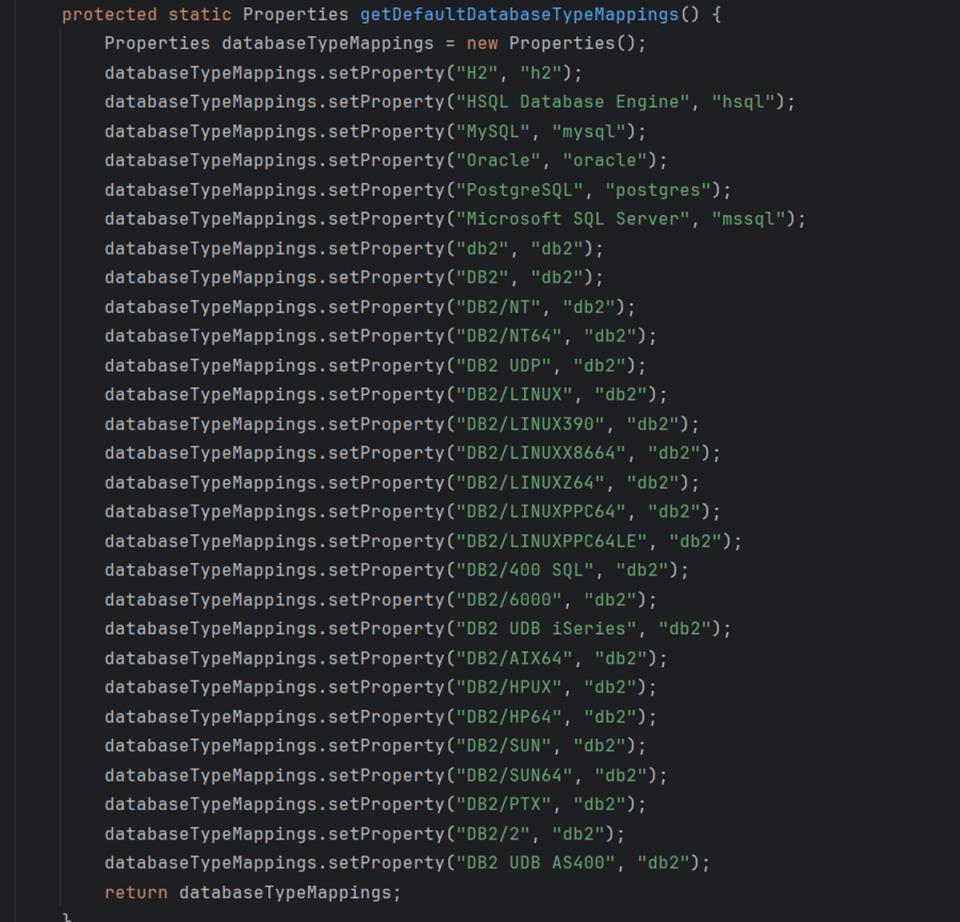
可以看到，并不支持yashandb。所以yashandb的jdbc驱动要加一个配置参数productName，可以在这种情况下返回Oracle。

经验总结

如下java代码可以检测当前jdbc驱动是否支持productName参数：

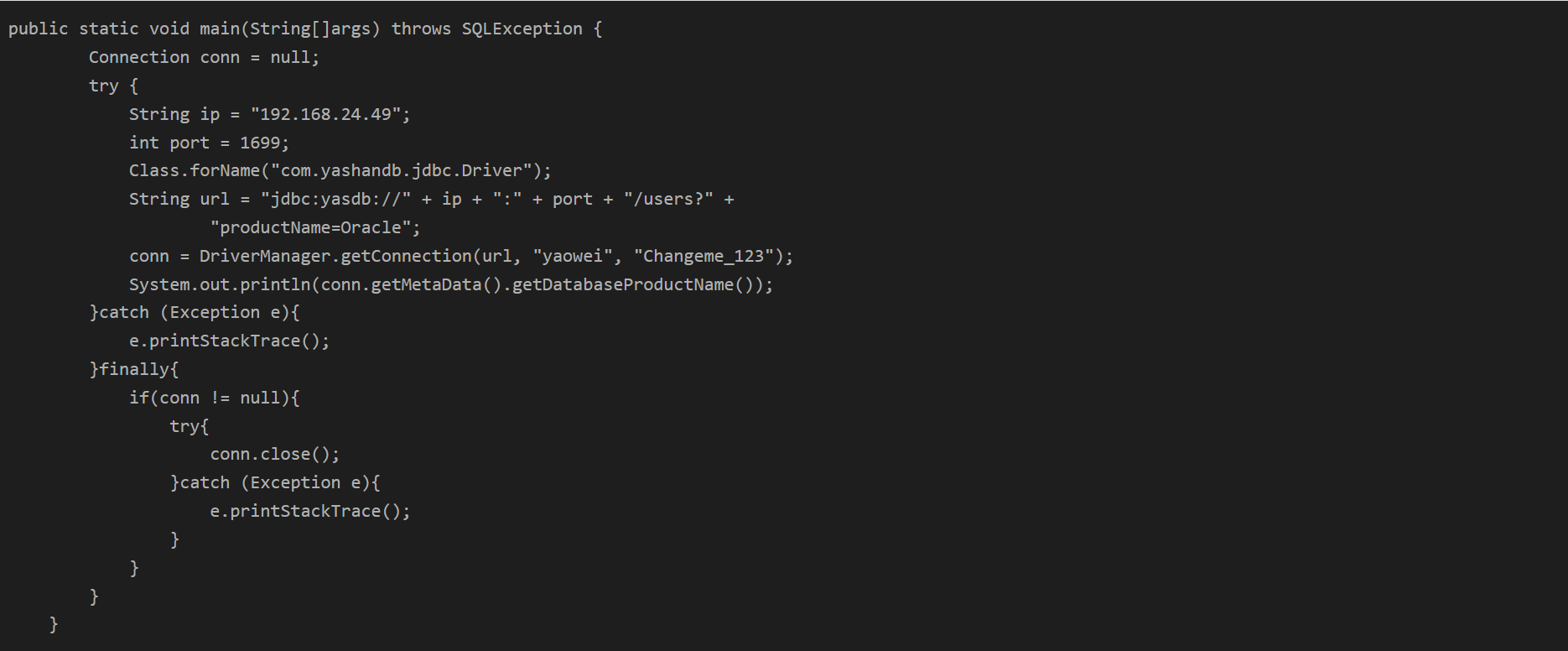
如果输出为Oracle，那么支持；如果输出为YashanDB，那么不支持。