【算法】DFS 系列之 穷举/暴搜/深搜/回溯/剪枝(上篇)
【ps】本篇有 9 道 leetcode OJ。
目录
一、算法简介
二、相关例题
1)全排列
.1- 题目解析
.2- 代码编写
2)子集
.1- 题目解析
.2- 代码编写
3)找出所有子集的异或总和再求和
.1- 题目解析
.2- 代码编写
4)全排列 II
.1- 题目解析
.2- 代码编写
5)电话号码的字母组合
.1- 题目解析
.2- 代码编写
6)括号生成
.1- 题目解析
.2- 代码编写
7)组合
.1- 题目解析
.2- 代码编写
8)目标和
.1- 题目解析
.2- 代码编写
9)组合总和
.1- 题目解析
.2- 代码编写
一、算法简介
回溯算法是一种经典的递归算法,通常⽤于解决组合问题、排列问题和搜索问题等。
回溯算法的基本思想:从一个初始状态开始,按照⼀定的规则向前搜索,当搜索到某个状态无法前进时,回退到前一个状态,再按照其他的规则搜索。回溯算法在搜索过程中维护一个状态树,通过遍历状态树来实现对所有可能解的搜索。
回溯算法的核心思想:“试错”,即在搜索过程中不断地做出选择,如果选择正确,则继续向前搜索,否则,回退到上一个状态,重新做出选择。回溯算法通常用于解决具有多个解,且每个解都需要搜索才能找到的问题。
// 回溯算法的模板
void dfs(vector<int>& path, vector<int>& choice, ...)
{// 满⾜结束条件if (/* 满⾜结束条件 */){// 将路径添加到结果集中res.push_back(path);return;}// 遍历所有选择for (int i = 0; i < choices.size(); i++){// 做出选择path.push_back(choices[i]);// 做出当前选择后继续搜索dfs(path, choices);// 撤销选择path.pop_back();}
}其中, path 表示当前已经做出的选择, choices 表示当前可以做的选择。在回溯算法中,我们需要做出选择,然后递归地调用回溯函数。如果满足结束条件,则将当前路径添加到结果集中。
否则,我们需要撤销选择,回到上一个状态,然后继续搜索其他的选择。回溯算法的时间复杂度通常较高,因为它需要遍历所有可能的解。但是,回溯算法的空间复杂度较低,因为它只需要维护一个状态树。在实际应用中,回溯算法通常需要通过剪枝等方法进行优化,以减少搜索的次数,从而提高算法的效率。
回溯算法是一种非常重要的算法,可以解决许多组合问题、排列问题和搜索问题等。回溯算法的核心思想是搜索状态树,通过遍历状态树来实现对所有可能解的搜索。回溯算法的模板非常简单,但是实现起来需要注意一些细节,比如何做出选择、如何撤销选择等。
二、相关例题
1)全排列
46. 全排列
.1- 题目解析
全排列的过程,其实可以画成一棵决策树,而找出全排列的结果,其实就是对这棵决策树进行 DFS。
DFS 的思路是,循环模仿遍历树的结点,到叶子结点就返回,不是就进入循环。
在下面 for 循环里要考虑这个位置要填哪个数。根据题目要求,我们肯定不能填已经填过的数,因此很容易想到的一个处理手段就是,定义一个标记数组来标记已经填过的数,那么在填这个数的时候,我们遍历题目给定的所有数,如果这个数没有被标记过,我们就尝试填入,并将其标记,继续尝试填下一个位置。而回溯的时候,要撤销这一个位置填的数以及标记,并继续尝试其他没被标记过的数。
.2- 代码编写
class Solution {vector<vector<int>> ret;vector<int> path;bool check[7];
public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size()==nums.size()){ret.push_back(path);return ;}for(int i=0;i<nums.size();i++)//枚举每一个在排列开头的数{if(check[i]==false){//记录结果并遍历下一层path.push_back(nums[i]);check[i]=true;dfs(nums);//回到这一层再恢复现场path.pop_back();check[i]=false;}}}
};2)子集
78. 子集
.1- 题目解析
本题有两种解法。
第一种与上一道题类似,根据某一个元素选或不选,将所有的子集穷举出来,然后统计结果即可。
第二种解法则是根据子集中有多少个元素,来将所有的子集穷举出来。
.2- 代码编写
//解法一
class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int i){if(i==nums.size()){ret.push_back(path);return;}//不选dfs(nums,i+1);//选path.push_back(nums[i]);//记录结果dfs(nums,i+1);path.pop_back();//恢复现场}
};//解法二
class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){ret.push_back(path);//每次进到下一层,都是新结果,都要记录for(int i=pos;i<nums.size();i++)//枚举下一层{path.push_back(nums[i]);//记录结果dfs(nums,i+1); //进入下一层path.pop_back(); //回到当前层,恢复现场}}
};3)找出所有子集的异或总和再求和
1863. 找出所有子集的异或总和再求和
.1- 题目解析
这道题只需要在上一道的基础上,稍微改变统计结果的方式即可。
.2- 代码编写
class Solution {int sum;int path;
public:int subsetXORSum(vector<int>& nums) {dfs(nums,0);return sum;}void dfs(vector<int>& nums,int pos){sum+=path;for(int i=pos;i<nums.size();i++){path^=nums[i];dfs(nums,i+1);path^=nums[i];}}
};4)全排列 II
47. 全排列 II
.1- 题目解析
我们可以直接在上文《全排列》的基础上用 set 对结果去重。
或者,在上文《全排列》的基础上,加入剪枝操作。由于题目不要求返回的排列顺序,因此我们可以对初始状态排序,将所有相同的元素放在各自相邻的位置,方便之后操作。
.2- 代码编写
//解法一:set去重
class Solution {set<vector<int>> ret;vector<int> path;bool cheak[8] = {false};
public:vector<vector<int>> permuteUnique(vector<int>& nums) {dfs(nums);vector<vector<int>> tmp(ret.begin(), ret.end());return tmp;}void dfs(vector<int> nums){if(nums.size() == path.size()){// if(find(ret.begin(), ret.end(), path) == ret.end())// ret.push_back(path);ret.insert(path);return;}for(int i = 0; i < nums.size(); ++i){if(cheak[i] == false) // 如果没有用过{path.push_back(nums[i]);cheak[i] = true;dfs(nums); // 此时路径已经加上一个了,在让其进入递归path.pop_back(); // 回溯,恢复现场,(递归往回走了)cheak[i] = false;}}}
};//解法二:剪枝,关心不合法的分支
class Solution {vector<int> path;vector<vector<int>> ret;bool check[9];
public:vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size()==nums.size()){ret.push_back(path);return;}for(int i=0;i<nums.size();i++){if(check[i]==true|| (i!=0 && nums[i]==nums[i-1] && check[i-1]==false)){continue;}path.push_back(nums[i]);check[i]=true;dfs(nums);path.pop_back();check[i]=false;}}
};//解法三:剪枝,关心合法的分支
//解法二:剪枝
class Solution {vector<int> path;vector<vector<int>> ret;bool check[9];
public:vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size()==nums.size()){ret.push_back(path);return;}for(int i=0;i<nums.size();i++){if(check[i]==false && (i==0 || nums[i]!=nums[i-1] || check[i-1]==true))//剪枝{path.push_back(nums[i]);check[i]=true;dfs(nums);path.pop_back();check[i]=false;}}}
};5)电话号码的字母组合
17. 电话号码的字母组合
.1- 题目解析
每一个数字都对应了一串字符,我们可以由此用一个哈希表建立数字和字符之间的映射,以便通过数字找到相应的字符。
而其他过程同上文中的题目,通过画决策树 + DFS 来解决。
.2- 代码编写
class Solution {string hash[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};vector<string> ret;string path;
public:vector<string> letterCombinations(string digits) {if(digits.size()==0)return ret;dfs(digits,0);return ret;}void dfs(string& digits,int pos){if(pos==digits.size()){ret.push_back(path);return;}for(auto ch:hash[digits[pos]-'0']){path.push_back(ch);dfs(digits,pos+1);path.pop_back();}}
};6)括号生成
22. 括号生成
.1- 题目解析
.2- 代码编写
class Solution {int left,right,n;string path;vector<string> ret;
public:vector<string> generateParenthesis(int _n) {n=_n;dfs();return ret;}void dfs(){if(right==n){ret.push_back(path);return ;}if(left<n){path.push_back('(');left++;dfs();path.pop_back();left--;}if(right<left){path.push_back(')');right++;dfs();path.pop_back();right--;}}
};7)组合
77. 组合
.1- 题目解析
本题是上一道题的变形,画决策树穷举出所有情况即可。
.2- 代码编写
class Solution {vector<int> path;vector<vector<int>> ret;int n,k;
public:vector<vector<int>> combine(int _n, int _k) {n=_n,k=_k;dfs(1);return ret;}void dfs(int start){if(path.size()==k){ret.push_back(path);return;}for(int i=start;i<=n;i++){path.push_back(i);dfs(i+1);path.pop_back();}}
};8)目标和
494. 目标和
.1- 题目解析
.2- 代码编写
class Solution {
int ret,aim;
public:int findTargetSumWays(vector<int>& nums, int target) {aim=target;dfs(nums,0,0);//参数:原始数组、当前下标位置、决策树某一条路径之和return ret;}void dfs(vector<int>& nums,int pos,int path){if(pos==nums.size()){if(path==aim)ret++;//统计结果return;}dfs(nums,pos+1,path+nums[pos]);//穷举加dfs(nums,pos+1,path-nums[pos]);//穷举减}
};9)组合总和
39. 组合总和
.1- 题目解析
.2- 代码编写
//解法一:枚举每个值之和
class Solution {int aim;vector<int> path;vector<vector<int>> ret;
public:vector<vector<int>> combinationSum(vector<int>& nums, int target) {aim=target;dfs(nums,0,0);return ret;}void dfs(vector<int>& nums,int pos,int sum){if(sum==aim){ret.push_back(path);return;}if(sum>aim || pos==nums.size())return;//回溯for(int i=pos;i<nums.size();i++){path.push_back(nums[i]);dfs(nums,i,sum+nums[i]);path.pop_back();}}
};//解法二:枚举每个值的个数
class Solution {int aim;vector<int> path;vector<vector<int>> ret;
public:vector<vector<int>> combinationSum(vector<int>& nums, int target) {aim=target;dfs(nums,0,0);return ret;}void dfs(vector<int>& nums,int pos,int sum){if(sum==aim){ret.push_back(path);return;}if(sum>aim || pos==nums.size())return;//回溯for(int k=0;k*nums[pos]<=aim;k++) //枚举个数{if(k)path.push_back(nums[pos]);dfs(nums,pos+1,sum+k*nums[pos]);}for(int k=1;k*nums[pos]<=aim;k++){path.pop_back();}}
};相关文章:

【算法】DFS 系列之 穷举/暴搜/深搜/回溯/剪枝(上篇)
【ps】本篇有 9 道 leetcode OJ。 目录 一、算法简介 二、相关例题 1)全排列 .1- 题目解析 .2- 代码编写 2)子集 .1- 题目解析 .2- 代码编写 3)找出所有子集的异或总和再求和 .1- 题目解析 .2- 代码编写 4)全排列 II…...

怎么绕开华为纯净模式安装软件
我是标题 众所周不知,华为鸿蒙系统自带纯净模式,而且 没法关闭 : ) 我反正没找到关闭键 以前或许会有提示,无视风险,“仍要安装”。但我这次遇到的问题是,根本没有这个选项,只有“应用市场”和“取消”&…...

CentOS7 离线部署docker和docker-compose环境
一、Docker 离线安装 1. 下载docker tar.gz包 下载地址: Index of linux/static/stable/x86_64/ 本文选择版本:23.0.6 2.创建docker.service文件 vi docker.service文件内容如下: [Unit] DescriptionDocker Application Container Engi…...

Vue 自定义组件实现 v-model 的几种方式
前言 在 Vue 中,v-model 是一个常用的指令,用于实现表单元素和组件之间的双向绑定。当我们使用原生的表单元素时,直接使用 v-model 是很方便的,但是对于自定义组件来说,要实现类似的双向绑定功能就需要一些额外的处理…...

Python Pandas数据处理效率提升指南
大家好,在数据分析中Pandas是Python中最常用的库之一,然而当处理大规模数据集时,Pandas的性能可能会受到限制,导致数据处理变得缓慢。为了提升Pandas的处理速度,可以采用多种优化策略,如数据类型优化、向量…...

最大正方形 Python题解
最大正方形 题目描述 在一个 n m n\times m nm 的只包含 0 0 0 和 1 1 1 的矩阵里找出一个不包含 0 0 0 的最大正方形,输出边长。 输入格式 输入文件第一行为两个整数 n , m ( 1 ≤ n , m ≤ 100 ) n,m(1\leq n,m\leq 100) n,m(1≤n,m≤100),接…...

ubuntu中软件的进程管理-结束软件运行
在Ubuntu系统中,当某个运行中的软件无法正常退出时,可以通过以下几种方法强制结束该软件: 方法一:使用系统监视器(System Monitor)–小白专属 这个相当于win上的资源管理器 打开系统监视器 可以通过点击屏…...

Windows环境部署Oracle 11g
Windows环境部署Oracle 11g 1.安装包下载2. 解压安装包3. 数据库安装3.1 执行安装脚本3.2 电子邮件设置3.3 配置安装选项3.4 配置系统类3.5 选择数据库安装类型3.6 选择安装类型3.7 数据库配置3.8 确认安装信息3.9 设置口令 Oracle常用命令 2023年10月中旬就弄出大致的文章&…...

C语言进阶【8】--联合体和枚举(联合体和枚举这么好用,你不想了解一下吗?)
本章概述 联合体类型的声明联合体的特点联合体的大小的计算枚举类型的声明枚举类型的优点枚举类型的使用枚举类型的大小彩蛋时刻!!! 联合体类型的声明 概述:联合体的关键字为 union。它的结构和结构体是一样的。进行展示…...

Android OTA升级
针对Android系统OTA升级,MTK平台有相关介绍文档:https://online.mediatek.com/apps/faq/detail?faqidFAQ27117&listSW 概念一:OTA包的构建 AOSP full build:Android原生提供的全量包的构建,意思就是可以从任何一…...
【项目经验分享】深度学习自然语言处理技术毕业设计项目案例定制
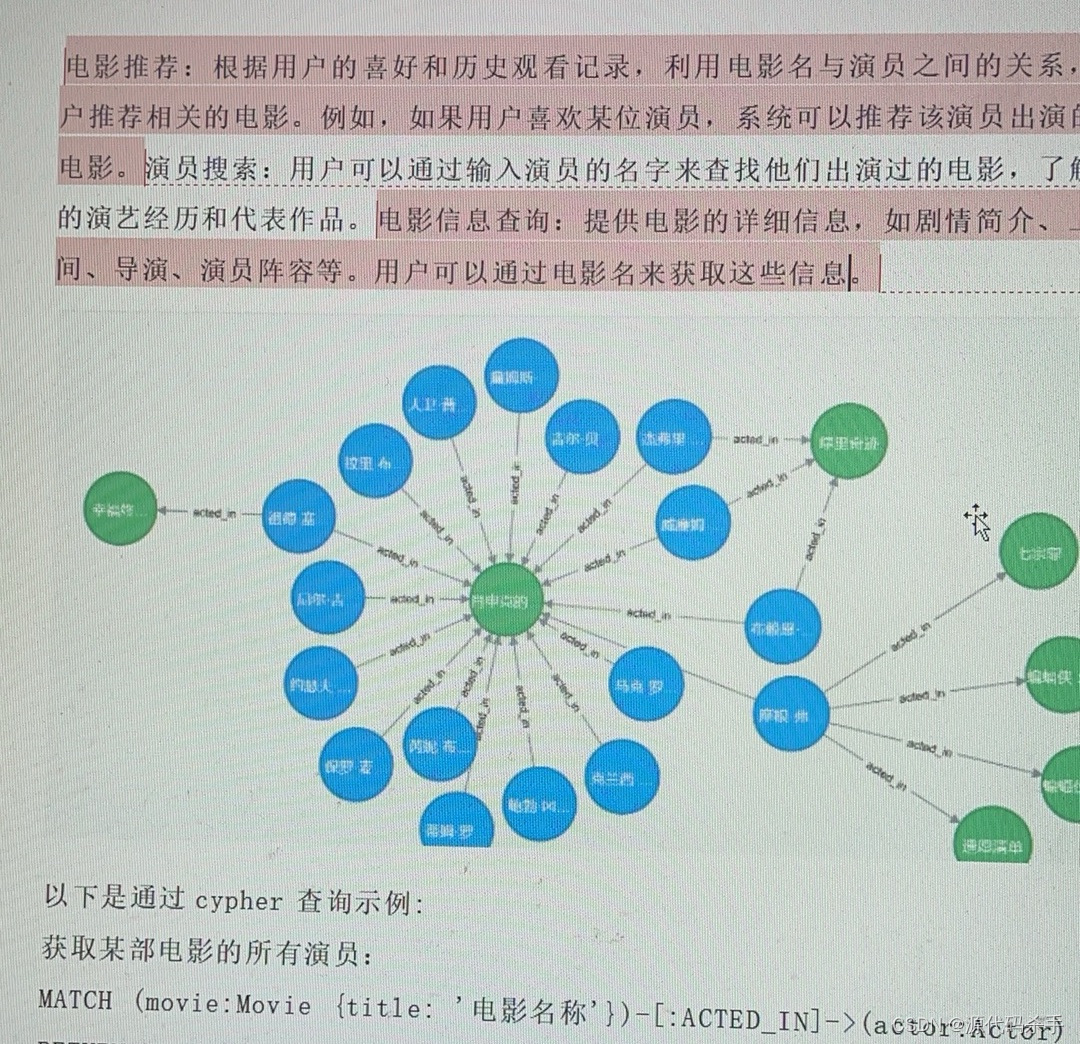
以下毕业设计是与深度学习自然语言处理(NLP)相关的毕业设计项目案例,涵盖文本分类、生成式模型、语义理解、机器翻译、对话系统、情感分析等多个领域: 实现案例截图: 基于深度学习的文本分类系统基于BERT的情感分析系…...

一觉醒来,YOLO11 冷不丁就来了
🥇 版权: 本文由【墨理学AI】原创首发、各位读者大大、敬请查阅、感谢三连 🎉 声明: 作为全网 AI 领域 干货最多的博主之一,❤️ 不负光阴不负卿 ❤️ 文章目录 前言:一觉醒来,YOLO11 冷不丁就来了ultralytics 版本更新…...

智能编辑器、版本控制与自动化脚本
在繁忙的工作中,每个开发者都渴望拥有一个“秘密武器”,帮助自己提升效率、减少错误,从而更快地完成任务。那么,在众多编程工具中,哪一款能够成为你的工作效率翻倍的“秘密武器”呢?本文将探讨智能的代码编…...

jenkinsfile实现镜像构建、发布
实现代码打包编译 容器镜像构建 jenkins编译采用docker构建。 遇到问题: 1.需要限制docker 容器的内存和cpu docker { image ‘ccr.ccs.tencentyun.com/libary/maven:3.6.3-jdk-8’ args “-v ${WORKSPACE}:/workspace --memory‘2048m’ --cpus‘1’” } 2.jenkins构建需要限制…...

OSPF路由计算
关于OSPF路由的基础概述可以看看这篇博客 动态路由---OSPF协议基础https://blog.csdn.net/ZZZCY2003/article/details/141335261 区域内路由计算 LSA概述 LSA是OSPF进行路由计算的关键依据OSPF的LSU报文可以携带多种不同类型的LSA各种类型的LSA拥有相同的报文头部 重要字段解…...

【设计模式-迭代】
定义 迭代器模式(Iterator Pattern)是一种行为型设计模式,用于提供一种顺序访问集合对象元素的方式,而不暴露该对象的内部表示。通过迭代器,客户端可以在不需要了解集合实现的细节的情况下遍历集合中的元素。 UML图 …...
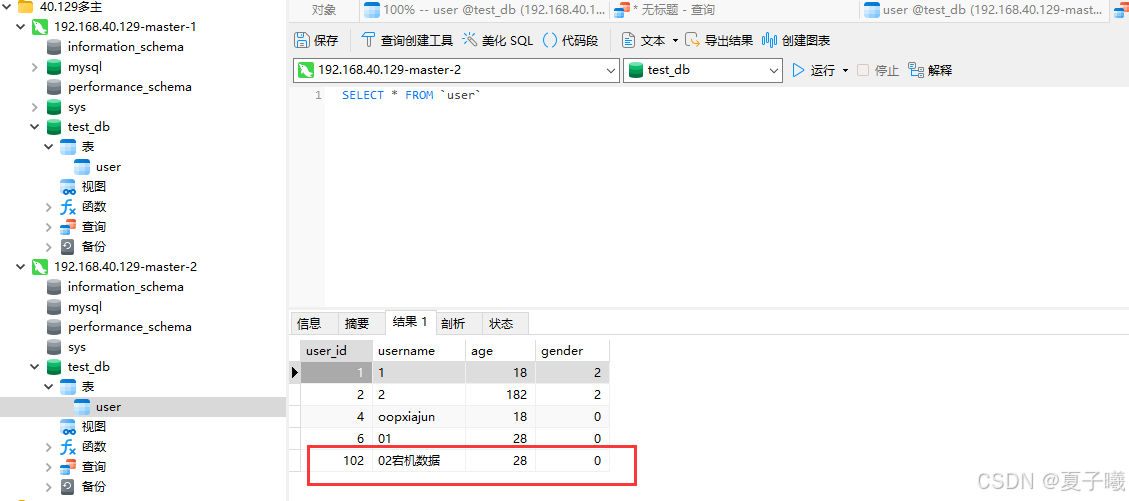
k8s搭建双主的mysql8集群---无坑
《k8s搭建一主三从的mysql8集群---无坑-CSDN博客》通过搭建一主三从,我们能理解到主节点只有1个,那么承担增删改主要还是主节点,如果你在从节点上去操作增删改操作,数据不会同步到其他节点。本章我们将实现多主(双主&a…...

Iterm2配置主题和Oh-My-Zsh
文章目录 一、配置主题1.1 安装使用git1.2 安装手册1.2.1 激活使用主题 二、配置oh-my-zsh2.1、oh-my-zsh插件2.2、oh-my-zsh主题 [Zsh](http://zsh.org/)2.2.1、Install using Git2.2.2、Install manually2.2.3、Activating theme2.2.4、Install using [zplug](https://github…...

html+css+js实现step进度条效果
实现效果 代码实现 HTML部分 <div class"box"><ul class"step"><li class"circle actives ">1</li><li class"circle">2</li><li class"circle">3</li><li class&quo…...
视频采集类VideoCapture之从视频源中读取一帧图像函数read()的使用)
OpenCV视频I/O(8)视频采集类VideoCapture之从视频源中读取一帧图像函数read()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 抓取、解码并返回下一个视频帧。 cv::VideoCapture::read() 是 VideoCapture 类的一个成员函数,用于从视频源中读取一帧图像. 该方法…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
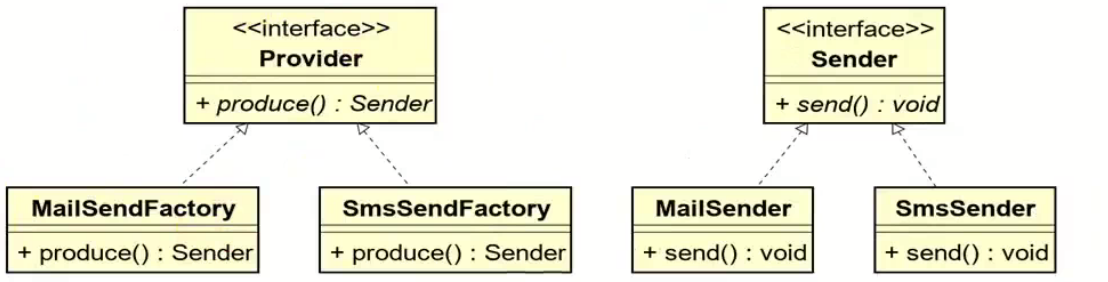
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...



















