STL之stackqueue篇(上)探索C++ STL中的Queue与Stack——构建数据处理的基础框架
文章目录
- 前言
- 一、stack
- 1.1 定义与基本概念
- 1.2 底层容器
- 1.3 成员函数
- 1.4 使用示例
- 1.5 注意事项
- 1.6 应用场景
- 二、queue
- 2.1 定义与基本概念
- 2.2 底层容器
- 2.3 成员函数
- 2.4 使用示例
- 2.5 注意事项
- 2.6 应用场景
前言
本文旨在深入探讨C++ STL中的queue与stack容器,从它们的基本概念、底层实现、成员函数到应用场景,全方位解析这两个容器的魅力所在。我们将通过生动的示例和详细的解释,帮助读者理解queue与stack的工作原理,掌握它们的使用方法,并启发读者在实际编程中灵活运用这两个容器,解决复杂的数据处理问题。
无论你是C++编程的初学者,还是有一定经验的开发者,本文都将为你提供一个全面、深入的视角,让你在数据结构的海洋中,找到属于自己的导航灯塔。让我们一起踏上这段探索之旅,共同领略queue与stack带来的编程魅力吧!
一、stack
1.1 定义与基本概念
stack是C++ STL中的一个容器适配器,它提供了一种后进先出(LIFO, Last In First Out)的数据结构。作为容器适配器,stack是对特定容器类进行封装,并提供了一组特定的成员函数来访问其元素。这些元素只能被添加(push)到容器的“顶部”,也只能从“顶部”移除(pop)。
1.2 底层容器
stack的底层容器可以是任何支持以下操作的容器类模板:
empty():判空操作。back():获取尾部元素操作。push_back():尾部插入元素操作。pop_back():尾部删除元素操作。
标准容器vector、deque、list均符合这些需求。默认情况下,如果没有为stack指定特定的底层容器,它将使用deque。
1.3 成员函数
stack提供了以下常用的成员函数:
push(const T& x):向栈顶添加一个元素。pop():移除栈顶元素。top():返回栈顶元素的引用。empty():检查栈是否为空。size():返回栈中元素的数量。
1.4 使用示例
以下是一个简单的使用stack的示例:
#include <iostream>
#include <stack> int main() { std::stack<int> myStack; // 向栈中添加元素 myStack.push(10); myStack.push(20); myStack.push(30); // 访问栈顶元素 std::cout << "栈顶元素: " << myStack.top() << std::endl; // 输出 30 // 移除栈顶元素 myStack.pop(); std::cout << "出栈后栈顶元素: " << myStack.top() << std::endl; // 输出 20 // 检查栈是否为空 if (myStack.empty()) { std::cout << "栈为空" << std::endl; } else { std::cout << "栈不为空" << std::endl; // 输出这个 } // 获取栈的大小 std::cout << "栈的大小: " << myStack.size() << std::endl; // 输出 2 return 0;
}
1.5 注意事项
- 栈顶元素访问:使用
top()函数可以访问栈顶元素,但该函数不删除栈顶元素。如果栈为空,调用top()函数将导致未定义行为。 - 栈的修改:
push()函数用于向栈中添加元素,而pop()函数用于移除栈顶元素。这两个函数都修改了栈的内容。 - 异常安全性:STL中的
stack容器是异常安全的。如果在添加或删除元素时发生异常,stack将保持其有效性。 - 内存管理:默认情况下,
stack使用deque作为其底层容器,因此其内存管理策略与deque相同。如果需要自定义内存管理策略,可以使用自定义的分配器。
1.6 应用场景
stack容器在以下场景中非常有用:
- 函数调用栈:在编译器和操作系统中,函数调用栈用于存储函数调用信息,包括参数、局部变量和返回地址。
- 表达式求值:在编译器中,可以使用栈来求值后缀表达式(逆波兰表示法)。
- 深度优先搜索(DFS):在算法和数据结构中,栈常用于实现深度优先搜索算法。
- 撤销操作:在某些应用程序中,可以使用栈来存储用户的操作历史,以便在需要时撤销操作。
综上所述,C++ STL中的stack容器是一个功能强大且易于使用的数据结构,它提供了后进先出的特性,并广泛应用于各种场景。
二、queue
2.1 定义与基本概念
queue是C++ STL中的一个容器适配器,它提供了一种先进先出(FIFO, First In First Out)的数据结构。与stack类似,queue也是对特定容器类进行封装,并提供了一组特定的成员函数来访问其元素。这些元素只能被添加(enqueue)到容器的“尾部”,也只能从“头部”移除(dequeue)。
2.2 底层容器
queue的底层容器可以是任何支持以下操作的容器类模板:
empty():判空操作。front():获取头部元素操作。back():获取尾部元素操作。push_back():尾部插入元素操作。pop_front():头部删除元素操作(注意,这里的描述是为了与queue的操作对应,实际上queue没有直接的pop_front()成员函数,而是通过pop()实现头部删除)。
标准容器deque、list以及vector(尽管vector在头部删除时效率不高,但理论上仍可作为底层容器)均符合这些需求。默认情况下,如果没有为queue指定特定的底层容器,它将使用deque。
2.3 成员函数
queue提供了以下常用的成员函数:
push(const T& x):向队列尾部添加一个元素。pop():移除队列头部元素。front():返回队列头部元素的引用。back():返回队列尾部元素的引用。empty():检查队列是否为空。size():返回队列中元素的数量。
2.4 使用示例
以下是一个简单的使用queue的示例:
#include <iostream>
#include <queue> int main() { std::queue<int> myQueue; // 向队列中添加元素 myQueue.push(10); myQueue.push(20); myQueue.push(30); // 访问队列头部元素 std::cout << "队列头部元素: " << myQueue.front() << std::endl; // 输出 10 // 访问队列尾部元素 std::cout << "队列尾部元素: " << myQueue.back() << std::endl; // 输出 30 // 移除队列头部元素 myQueue.pop(); std::cout << "出队后队列头部元素: " << myQueue.front() << std::endl; // 输出 20 // 检查队列是否为空 if (myQueue.empty()) { std::cout << "队列为空" << std::endl; } else { std::cout << "队列不为空" << std::endl; // 输出这个 } // 获取队列的大小 std::cout << "队列的大小: " << myQueue.size() << std::endl; // 输出 2 return 0;
}
2.5 注意事项
- 队列元素访问:使用
front()函数可以访问队列头部元素,使用back()函数可以访问队列尾部元素,但这两个函数都不删除元素。如果队列为空,调用front()或back()函数将导致未定义行为。 - 队列的修改:
push()函数用于向队列中添加元素,而pop()函数用于移除队列头部元素。这两个函数都修改了队列的内容。 - 异常安全性:STL中的
queue容器是异常安全的。如果在添加或删除元素时发生异常,queue将保持其有效性。 - 不支持迭代器:与
stack类似,queue也不支持迭代器,因此不能使用迭代器来遍历队列中的元素。 - 内存管理:默认情况下,
queue使用deque作为其底层容器,因此其内存管理策略与deque相同。如果需要自定义内存管理策略,可以使用自定义的分配器。
2.6 应用场景
queue容器在以下场景中非常有用:
- 任务调度:在操作系统和并发编程中,
queue常用于存储待处理的任务或事件。 - 广度优先搜索(BFS):在算法和数据结构中,
queue常用于实现广度优先搜索算法。 - 消息传递:在进程间通信或线程间通信中,
queue可用于存储和传递消息。 - 缓存管理:在某些应用场景中,
queue可用于实现带有限制大小的缓存,当缓存满时,可以移除最早添加的元素。
综上所述,C++ STL中的queue容器是一个功能强大且易于使用的数据结构,它提供了先进先出的特性,并广泛应用于各种场景。
相关文章:
探索C++ STL中的Queue与Stack——构建数据处理的基础框架)
STL之stackqueue篇(上)探索C++ STL中的Queue与Stack——构建数据处理的基础框架
文章目录 前言一、stack1.1 定义与基本概念1.2 底层容器1.3 成员函数1.4 使用示例1.5 注意事项1.6 应用场景 二、queue2.1 定义与基本概念2.2 底层容器2.3 成员函数2.4 使用示例2.5 注意事项2.6 应用场景 前言 本文旨在深入探讨C STL中的queue与stack容器,从它们的…...

代码随想录算法训练营Day13
110.平衡二叉树 力扣题目链接:. - 力扣(LeetCode) 后序迭代 class Solution {public boolean isBalanced(TreeNode root) {return getHeight(root)!-1;}public int getHeight(TreeNode root){if(rootnull){return 0;}int leftheightgetHei…...

基于STM32的智能门禁系统
目录 引言项目背景环境准备 硬件准备软件安装与配置系统设计 系统架构关键技术代码示例 RFID数据采集与处理门禁控制实现显示与报警功能应用场景结论 1. 引言 智能门禁系统在现代安防中占据重要地位,通常用于控制进入和离开特定区域的权限。通过基于STM32微控制器…...
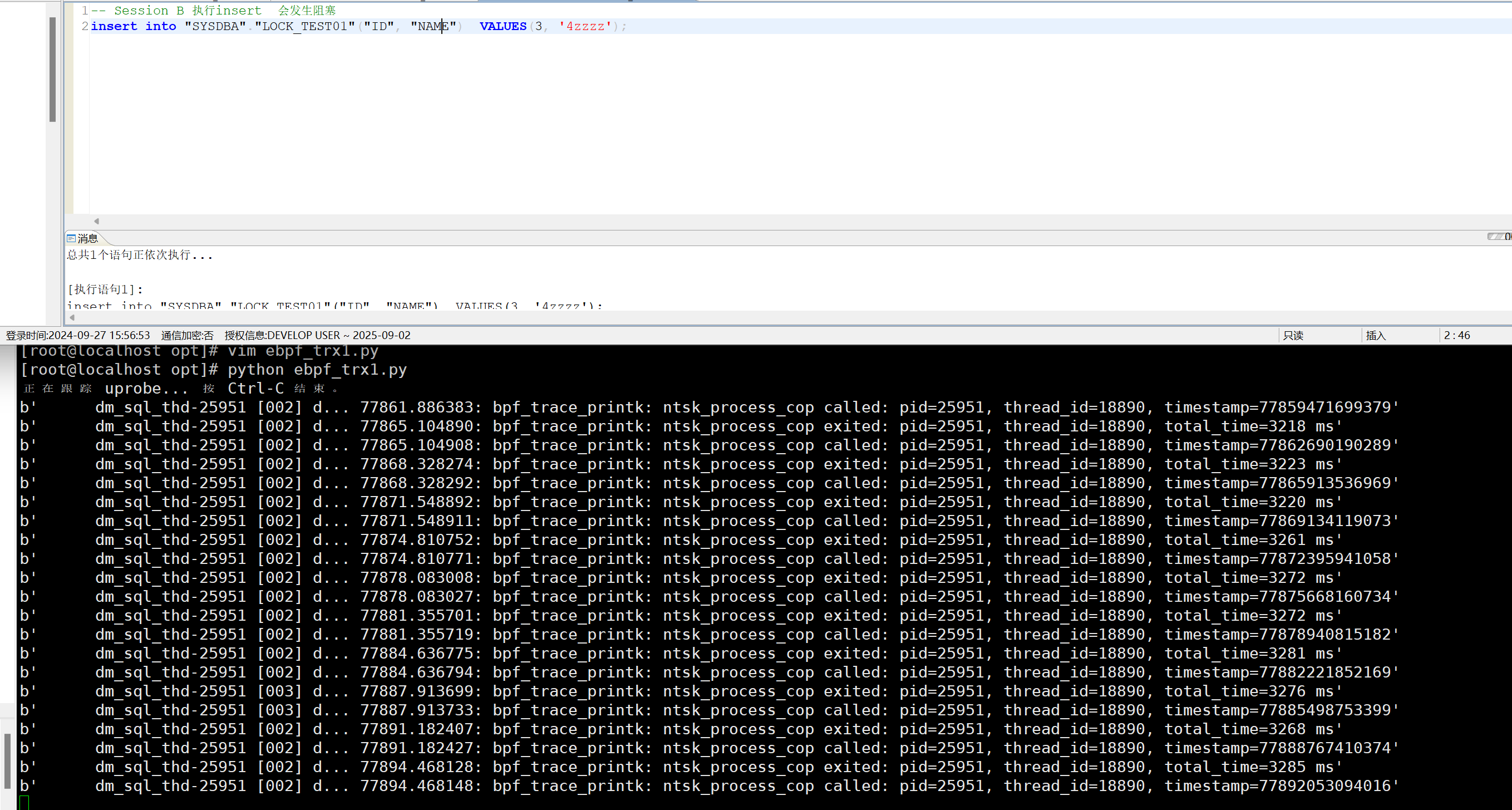
[EBPF] 实时捕获DM数据库是否存在SQL阻塞
1. 介绍 eBPF(extened Berkeley Packet Filter)是一种内核技术,它允许开发人员在不修改内核代码的情况下运行特定的功能。eBPF 的概念源自于 Berkeley Packet Filter(BPF),后者是由贝尔实验室开发的一种网…...

秋招内推--招联金融2025
【投递方式】 直接扫下方二维码,或点击内推官网https://wecruit.hotjob.cn/SU61025e262f9d247b98e0a2c2/mc/position/campus,使用内推码 igcefb 投递) 【招聘岗位】 后台开发 前端开发 数据开发 数据运营 算法开发 技术运维 软件测试 产品策…...

Unity2022.3.x各个版本bug集合及推荐稳定版本
最近升级到Unity2022,发现以下问题,仅作参考 2022.3.0f1 - 2022.3.6f1 粒子渲染到RenderTexture闪屏 https://issuetracker.unity3d.com/issues/android-vulkan-visualisation-corruption-occurs-when-rendering-particles-to-render-texture 2022.3.…...

SparkSQL-性能调优
祝福 在这个举国同庆的时刻,我们首先献上对祖国的祝福: 第一,我们感谢您给我们和平的环境,让我们能快乐生活 第二,祝福我们国家未来的路越走越宽广,科技更发达,人民更幸福 第三,…...
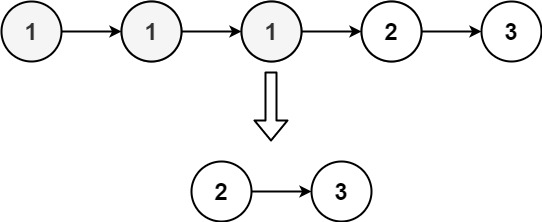
leetcode-链表篇
leetcode-707 你可以选择使用单链表或者双链表,设计并实现自己的链表。 单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。 如果是双向链表,则还需要属性 prev 以指示链表中的…...

JetLinks物联网平台微服务化系列文章介绍
橙蜂智能公司致力于提供先进的人工智能和物联网解决方案,帮助企业优化运营并实现技术潜能。公司主要服务包括AI数字人、AI翻译、AI知识库、大模型服务等。其核心价值观为创新、客户至上、质量、合作和可持续发展。 橙蜂智农的智慧农业产品涵盖了多方面的功能&#x…...

【QT Quick】基础语法:导入外部QML文件
在实际项目中,代码通常分为多个文件进行模块化管理,这样可以方便代码重用,例如统一风格或共享功能模块。我们将在此部分学习如何创建 QML 项目,并演示如何访问外部代码,包括其他 QML 文件、库文件以及 JS 代码。 准备…...

Llama 系列简介与 Llama3 预训练模型推理
1. Llama 系列简介 1.1 Llama1 由 Meta AI 发布,包含 7B、13B、33B 和 65B 四种参数规模的开源基座语言模型 数据集:模型训练数据集使用的都是开源的数据集,总共 1.4T token 模型结构:原始的 Transformer 由编码器(…...

【AIGC】ChatGPT提示词助力自媒体内容创作升级
博客主页: [小ᶻZ࿆] 本文专栏: AIGC | ChatGPT 文章目录 💯前言💯高效仿写专家级文章提示词使用方法 💯CSDN博主账号分析提示词使用方法 💯自媒体爆款文案优化助手提示词使用方法 💯小结 💯…...

SSTI基础
<aside> 💡 简介 </aside> 原理 又名:Flask模版注入 模版种类 **Twig{{7*7}}结果49 jinja2{{7*7}}结果为7777777 //jinja2的常见参数是name smarty7{*comment*}7为77**<aside> 💡 flask实例 </aside> **from …...

10.1软件工程知识详解上
软件工程概述 软件开发生命周期 软件定义时期:包括可行性研究和详细需求分析过程,任务是确定软件开发工程必须完成的总目标,具体可分成问题定义、可行性研究、需求分析等。软件开发时期:就是软件的设计与实现,可分成…...
)
03Frenet与Cardesian坐标系(Frenet转Cardesian公式推导)
Frenet转Cardesian 1 明确目标 已知车辆质点在Frenet坐标系下的状态: Frenet 坐标系下的纵向坐标: s s s纵向速度: s ˙ \dot{s} s˙纵向加速度: s \ddot{s} s横向坐标: l l l横向速度: l ˙ \dot{l} l…...

knowLedge-Vue I18n 是 Vue.js 的国际化插件
1.简介 Vue I18n 是 Vue.js 的国际化插件,它允许开发者根据不同的语言环境显示不同的文本,支持多语言。 Vue I18n主要有两个版本:v8和v9。v8版本适用于Vue2框架。v9版本适用于Vue3框架。 2. 翻译实现原理 Vue I18n 插件通过在 Vue 实例中注…...

【开源免费】基于SpringBoot+Vue.JS微服务在线教育系统(JAVA毕业设计)
本文项目编号 T 060 ,文末自助获取源码 \color{red}{T060,文末自助获取源码} T060,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

expressjs 中的mysql.createConnection,execute 怎么使用
在 Express.js 应用中使用 MySQL 数据库,你通常会使用 mysql 或 mysql2 这样的库来创建和管理数据库连接,并执行查询。然而,mysql.createConnection 并不直接提供 execute 方法。相反,你可以使用 query 方法来执行 SQL 语句。 以…...

每日一题|983. 最低票价|动态规划、记忆化递归
本题求解最小值,思路是动态规划,但是遇到的问题是:动态规划更新的顺序和步长,以及可能存在的递归溢出问题。 1、确定dp数组含义 dp[i]表示第i天到最后一天(可能不在需要出行的天数里),需要花费…...

oracle 正则 匹配 身份正 手机号
1.正则匹配身份证号: regexp_like(card_id,^[1-9]\d{5}(18|19|20)?\d{2}(0[1-9]|1[0-2])(0[1-9]|[12]\d|3[01])\d{3}(\d|X)$) ^[1-9]\d{5}(18|19|20)?\d{2}(0[1-9]|1[0-2])(0[1-9]|[12]\d|3[01])\d{3}(\d|X)$ ^[1-9]:第一位数字不能为0。 \d{5}:接下来…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
