大二考核题解
大二考核题解
| 题号 | 题目 | 考察知识点 |
|---|---|---|
| A | 有意思的监考 | 二分答案 |
| B | 海绵宝宝的数独 | DFS |
| C | 走楼梯 | 递推 |
| D | 碱基配对 | kmp |
| E | 好简单的题啊,写它! | 最短路 |
写在前面: 整体难度不大,代码能力需要一些,正常来说至少要会3题以上
A 有意思的监考
找最小值的最大,标准的二分答案的模板,只需要重新写一下check函数
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 100;
int a[N];
int n;
bool check(int mid)
{int t = a[1] + mid, cnt = 1;for(int i = 2 ; i <= n ; i ++){if(a[i] - t > mid){cnt ++;t = a[i] + mid;}}return cnt <= 3;
}int main()
{int t;cin >> t;while(t--){cin >> n;//cout << "n:"<<n << endl;for(int i = 1 ; i <= n ; i ++) cin >> a[i];//cout << a[n] << "an\n";sort(a+1,a+n+1);int l = 0 , r = a[n];while(l < r){int mid = (l + r) >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << l << endl;}
}
B 海绵宝宝的数独
#include <iostream>
#include <vector>
// 检查当前填入的数字是否符合数独规则
bool isValid(std::vector<std::vector<int>>& board, int row, int col, int num) {
// 检查行和列for (int i = 0; i < 9; ++i) {if (board[row][i] == num || board[i][col] == num) {return false;}}
// 检查 3x3 区域int startRow = row - row % 3;int startCol = col - col % 3;for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) {if (board[i + startRow][j + startCol] == num) {return false;}}}return true;
}
// 使用回溯算法填充数独空格
bool solveSudoku(std::vector<std::vector<int>>& board) {for (int row = 0; row < 9; ++row) {for (int col = 0; col < 9; ++col) {if (board[row][col] == 0) {for (int num = 1; num <= 9; ++num) {if (isValid(board, row, col, num)) {board[row][col] = num;if (solveSudoku(board)) {return true;}board[row][col] = 0; // 回溯}}return false;}}}return true;
}
int main() {std::vector<std::vector<int>> board(9, std::vector<int>(9));
// 读取数独矩阵for (int i = 0; i < 9; ++i) {std::string row;std::cin >> row;for (int j = 0; j < 9; ++j) {board[i][j] = row[j] - '0'; // 将字符转换为对应的整数}}
// 解决数独solveSudoku(board);
// 输出填好的数独矩阵for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {std::cout << board[i][j];}std::cout << "\n";}return 0;
}
C 走楼梯
/*
* 本题主要考察递推的思想
* 题目中想要求的是走楼梯的最小花费,起始位置为 0 或 1 你可以选择向上走一步或者两步
* 实际我们可以从后往前进行分析, 假设我们是从下标为 n - 1 的位置开始,最小花费为 cost[n - 1]
* 如果从下标为 n - 2 的位置开始,最小花费为 cost[n - 2]
* 如果从下标为 n - 3 的位置开始,最小花费为 cost[n - 3] + min(cost[n - 2], cost[n - 1])
* 如果从下标为 n - 4 的位置开始,最小花费为 cost[n - 4] + min((cost[n - 3] + min(cost[n - 2], cost[n - 1])), cost[n - 2])
* 假设我们用数组 dp 来记录从下标为 i 的位置开始的最小花费值,很容易可以得到递推公式
* dp[i] = cost[i] + min(dp[i + 1], dp[i + 2])
* 得到递推公式之后,我们可以从后往前遍历数组 cost[i],从而倒推出 dp[0] 和 dp[1] 的值
* dp 数组的含义:从下标为 i 的位置开始的最小花费值,因此 min(dp[0], dp[1]) 即是我们想要的结果
* tips:min 函数为 C++ 自带的库函数,C语言并没有这个库函数,可以自己写一个
*/#include <iostream>
#include <cstring>using namespace std;const int N = 1e5 + 10;
int cost[N]; ///< 题目中给的cost数组
int dp[N]; ///< 从第 i 个位置开始走需要花费的最小值
int n;
// ---- min函数写法 ------
/*
int min(int a, int b)
{if (a > b) return b;return a;
}
*/
int main()
{ memset(dp, 0, sizeof dp); /// 将 dp 数组整体置 0 等同于 for(int i = 0; i < n; i ++ ) dp[i] = 0; cin >> n;for (int i = 0; i < n; i ++ ) {cin >> cost[i];}// 初始化递推数组 dp[n - 1] = cost[n - 1];dp[n - 2] = cost[n - 2];// 根据递公式进行计算for (int i = n - 3; i >= 0; i -- ) {dp[i] = cost[i] + min(dp[i + 1] , dp[i + 2]);}cout << min(dp[0], dp[1]) << endl;return 0;
}
另解
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e5 + 10;
int cost[N], f[N];
int main()
{int n;cin >> n;memset(f,0x3f,sizeof f);for(int i = 0 ; i < n ; i++) cin >> cost[i];f[0] = 0, f[1] = 0;for(int i = 2 ; i <= n ; i ++)f[i] = min(f[i-1]+cost[i-1],f[i-2]+cost[i-2]);cout << f[n];return 0;
}
D 碱基配对
思路: K M P KMP KMP算法遍历每一个子串
K M P KMP KMP基本思想:发生不匹配时,主串S的i不回溯,子串 T T T的j回溯到 n e x t [ j ] next[j] next[j]对应位置的 k k k上。
①用字符串数组存储每一组的碱基序列,数组的元素是一串碱基序列;
②从第一串碱基序列(字符串数组的第一个元素)入手,从最长的子串(碱基序列本身)开始与其他序列进行比对,直到找到共有的子串为止;
③暴力列举每一个子串进行比对,采用 K M P KMP KMP算法进行比较。
#include<bits/stdc++.h>
using namespace std;void getNext(string S,int* next) //得到子串下面的数组
{int j,k;j=0;k=-1;next[0]=-1; //子串0号元素下面数为-1while(j<(S.size()-1)) //对子串所有元素下面赋值{if(k==-1||S[j]==S[k]) //如果k回到了第一个元素或者第j个元素等于第k个元素{j++;k++; //j++;k++;next[j]=k; //子串第j个元素下面的数为k}elsek=next[k]; //k为第子串第k个元素下面的数}
}bool Compare(string T,string *S,int n) //返回该子串是否是每一个序列的子串
{int a=T.size(); //得到子串T的长度int next[a]; //建立子串的数组下标getNext(T,next); //给子串数组赋值int results[n]; //建立一个大小为n的数组判断子串是不是n-1个主串的公共子串for(int i=0;i<n;i++){results[i]=0; //给数组hhh全赋初值0}for(int l=1;l<n;l++){int aa=S[l].size(); //得到主串的长度int i=0,j=0;while(i<aa) //当主串下标没到达尾部时{if(j==-1||S[l][i]==T[j]){++i;++j;}elsej=next[j];if(j==a){results[l]=1;break;}}}for(int i=1;i<n;i++) //查看该子串是否为每一个主串下面的子串{if(results[i]!=1)return false; //不是则返回false}return true; //反之是则返回true
}void Deal(string *aar,int n)
{string key="Z"; //假定最长公共序列keystring try1; //第一个碱基序列的每一个字串int w=0;for(int i=60;i>=3;i--) //从最长字符串长度开始作为子串长度{if(w!=0&&i<w){cout<<key<<endl;return ;}for(int k=0;k<=60-i;k++) //开始位置{try1=aar[0].substr(k,i); //第一个碱基序列的一个字串//cout<<try1<<endl;if(Compare(try1,aar,n)) //查看是否为公共字串{w=i;if((try1.size()>=key.size())&&(try1<key))key=try1;}}}if(key.size()<3)cout<<"no significant commonalities"<<endl;elsecout<<key<<endl;
}int main()
{int N;cin>>N; //输入数据集合的数目Nfor(int z=0;z<N;z++) //输入集合的每一组元素{int n;cin>>n; //输入数据集合中碱基序列的数目nstring jjsz[n]; //建立jjsz[n]数组存放每一组碱基序列for(int x=0;x<n;x++){cin>>jjsz[x]; //存放每一个碱基序列}Deal(jjsz,n); //开始处理}return 0;
}
E 好简单的题啊,写它!
d i j k s t r a dijkstra dijkstra的模板,但需要注意路径长度可能会爆 i n t int int,需要开 l o n g l o n g long long longlong
#include<bits/stdc++.h>
#define ll long long
const int MaxN = 100010, MaxM = 500010;
const ll inf=0x3f3f3f3f3f;
struct edge
{int to, dis, next;
};edge e[MaxM];
ll head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
int n, m, s;inline void add_edge( int u, int v, int d )
{cnt++;e[cnt].dis = d;e[cnt].to = v;e[cnt].next = head[u];head[u] = cnt;
}struct node
{ll dis;ll pos;bool operator <( const node &x )const{return x.dis < dis;}
};std::priority_queue<node> q;inline void dijkstra()
{dis[s] = 0;q.push( ( node ){0, s} );while( !q.empty() ){node tmp = q.top();q.pop();int x = tmp.pos, d = tmp.dis;if( vis[x] )continue;vis[x] = 1;for( int i = head[x]; i; i = e[i].next ){int y = e[i].to;if( dis[y] > dis[x] + e[i].dis ){dis[y] = dis[x] + e[i].dis;if( !vis[y] ){q.push( ( node ){dis[y], y} );}}}}
}int main()
{scanf( "%d%d%d", &n, &m, &s );for(int i = 1; i <= n; ++i)dis[i] = inf;for( register int i = 0; i < m; ++i ){register int u, v, d;scanf( "%d%d%d", &u, &v, &d );add_edge( u, v, d );}dijkstra();for( int i = 1; i <= n; i++ )if(dis[i]!=inf) printf( "%lld ", dis[i] );else printf("inf ");return 0;
}
相关文章:

大二考核题解
大二考核题解 题号题目考察知识点A有意思的监考二分答案B海绵宝宝的数独DFSC走楼梯递推D碱基配对kmpE好简单的题啊,写它!最短路 写在前面: 整体难度不大,代码能力需要一些,正常来说至少要会3题以上 A 有意思的监考 …...

深入解析:Kubernetes 如何使用 etcd 作为配置中心和注册中心
在 Kubernetes 中,etcd 是核心的分布式存储组件,负责存储和管理集群的所有配置信息、状态数据以及服务注册信息。etcd 的高可用性和强一致性使得它成为 Kubernetes 的 “source of truth”,确保集群能够动态、高效地管理资源,并保…...

MQ高级:RabbitMQ小细节
在之前的学习中,我们只介绍了消息的发送,但是没有考虑到异常的情况,今天我们就介绍一些异常情况,和细节的部分。 目录 生产者可靠性 生产者重连 生产者确认 MQ可靠性 持久化 Lazy Queue 消费者可靠性 消费者确认机制 失…...
期权卖方怎么选择权利金高的品种,期货VIX高低对行情有什么影响
VIX指数——全称为芝加哥期权交易所市场波动率指数,俗称恐慌指数。 是衡量波动性的重要指标。VIX指数上升,预期未来市场波动性会增加。VIX指数下降,预期未来市场波动性会降低。 期货VIX指数最新价格排序 期权卖方尽量选择期货VIX指数在25以…...

内存对齐的原理和使用
1. 什么是内存对齐? 内存对齐是指将数据存储在内存中时,按照数据类型的大小,将数据放在特定的内存边界上。例如,4 字节的 int 通常放在能够被 4 整除的地址上,8 字节的 double 则放在能被 8 整除的地址上。 2. 为什么…...

搭建企业级私有仓库harbor
华子目录 harbor简介实验环境准备下载软件包安装docker-cehosts解析 实验步骤配置https加密传输解压进入解压目录,修改文件配置启动harbor 测试客户端配置harbor本地加速器注意 通过docker compose管理harbor harbor简介 harbor是由wmware公司开源的企业级docker r…...

互联网前后端分离的开发场景,一般会员和数据权限的判断是放在前端还是后端?
推荐学习文档 golang应用级os框架,欢迎stargolang应用级os框架使用案例,欢迎star案例:基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总想学习更多golang知识,这里有免费的golang学习笔…...

李宏毅机器学习2022-HW8-Anomaly Detection
文章目录 TaskBaselineReportQuestion2 Code Link Task 异常检测Anomaly Detection 将data经过Encoder,在经过Decoder,根据输入和输出的差距来判断异常图像。training data是100000张人脸照片,testing data有大约10000张跟training data相同…...

用户体验分享 | YashanDB V23.2.3安装部署
近期崖山新版体验过程中,总能看到用户提问:openssl版本问题、monit命令找不到问题、yashan用户权限问题、数据库重装问题 今日整理了多位用户的安装经验,希望能够帮助到大家~ 1.Lucifer三思而后行 :YashanDB 个人版数据库安装部…...

【漏洞复现】泛微OA E-Office /E-mobile/App/init.php 任意文件上传漏洞
免责声明: 本文旨在提供有关特定漏洞的信息,以帮助用户了解潜在风险。发布此信息旨在促进网络安全意识和技术进步,并非出于恶意。读者应理解,利用本文提到的漏洞或进行相关测试可能违反法律或服务协议。未经授权访问系统、网络或应用程序可能导致法律责任或严重后果…...
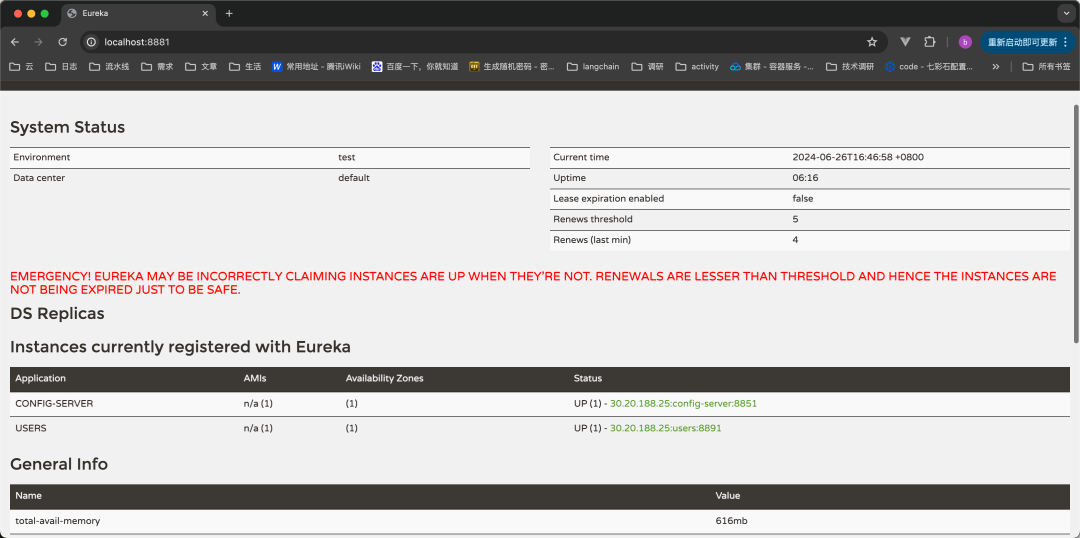
SpringCloudEureka实战:搭建EurekaServer
1、依赖引入 <dependencies><!-- 注册中心 --><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></dependency> </dependencies> <de…...
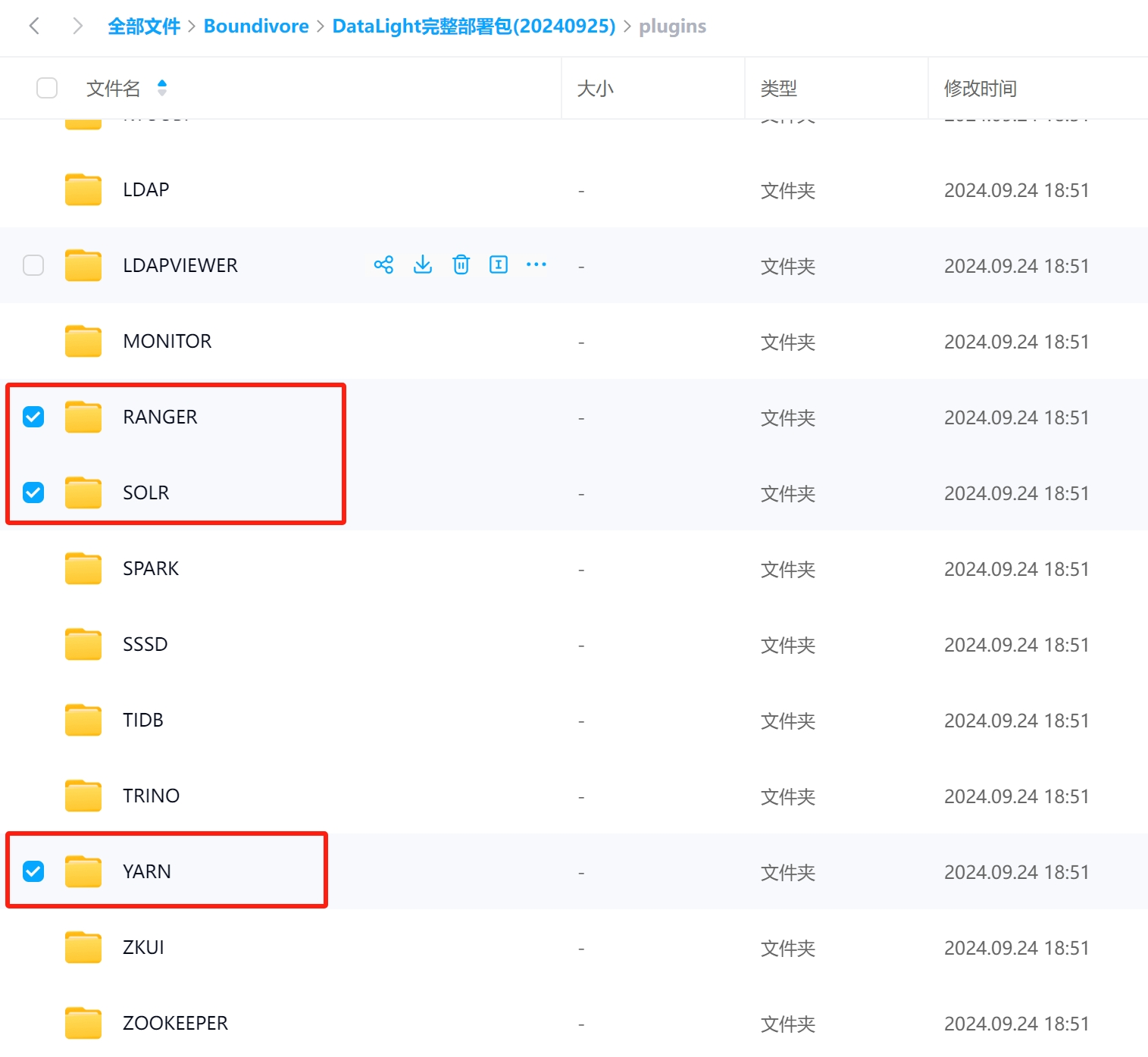
DataLight(V1.4.5) 版本更新,新增 Ranger、Solr
DataLight(V1.4.5) 版本更新,新增 Ranger、Solr DataLight 迎来了重大的版本更新,现已发布 V1.4.5 版本。本次更新对平台进行了较多的功能拓展和优化,新增了对 Ranger 和 Solr 服务组件的支持,同时对多项已…...

深度解析:Python蓝桥杯青少组精英赛道与高端题型概览
目录 一、蓝桥杯青少组简介二、赛项组别与年龄范围三、比赛内容与题型1. 基础知识范围2. 题型设置2.1 选择题2.2 编程题 3. 考试时长 四、奖项设置与激励措施五、总结 一、蓝桥杯青少组简介 蓝桥杯全国软件和信息技术专业人才大赛(简称“蓝桥杯”)是由工…...

如何使用SCCMSecrets识别SCCM策略中潜在的安全问题
关于SCCMSecrets SCCMSecrets是一款针对SCCM策略的安全扫描与检测工具,该工具旨在提供一种有关 SCCM 策略的全面安全检测方法。 该工具可以从各种权限级别执行,并将尝试发现与策略分发相关的潜在错误配置。除了分发点上托管的包脚本外,它还将…...

Qt 信号重载问题--使用lambda表达式--解决方法
在connect()中,使用lambda表达式时遇到信号重载,无法识别使用哪个参数时,可通过以下方法处理: 1. 使用QOverload: Qt5.7才有 connect(comboBox,QOverload<int>::of(&QComboBox::currentIndexChanged), [](int index)…...

并行编程实战——TBB框架的应用之一Supra的基础
一、TBB的应用 在前面分析了TBB框架的各种基本知识和相关的基础应用。这些基础的应用很容易通过学习文档或相关的代码来较为轻松的掌握。为了能够更好的理解TBB框架的优势,这里从一个开源的应用程序来分析一下TBB在其中的更高一层的抽象应用,以方便开发…...

std::vector
std::vector是C标准库中一个非常强大的容器类,它提供了动态数组的功能。std::vector可以自动调整大小,提供了随机访问的能力,同时还支持在序列的尾部高效地添加和删除元素。 当创建一个空的std::vector对象时,它不分配任何内存&a…...

Java Web 之 Cookie 详解
在 JavaWeb 开发中,Cookie 就像网站给浏览器贴的小纸条,用于记录一些用户信息或状态,方便下次访问时识别用户身份或进行个性化服务。 也可以这么理解: 场景一:想象一下,你去一家咖啡店,店员认…...

linux系统下让.py文件开机自启动
一 创建服务文件 1、打开终端 2、切换到root用户 sudo su3、创建一个新的systemd服务文件 nano /etc/systemd/system/total_test0619.service 4、在服务文件中添加以下内容 [Unit] DescriptionRun total_test0619.py at startup[Service] Typesimple ExecStart/usr/bin/n…...

linux远程桌面:xrdp 安装失败
window 如何远程 Linux 桌面 安装xrdp yum install xrdpsystemctl start xrdp 如果找不到软件包,就安装epel源,最好改成国内镜像的 在 /etc/yum.repos.d/ 下创建epel.repo,内容如下 [epel] nameExtra Packages for Enterprise Linux 7 - $basearch …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
