python 实现点的多项式算法
点的多项式算法介绍
点的多项式算法通常指的是通过一组点(即数据点,通常包括自变量和因变量的值)来拟合一个多项式函数的方法。这种方法在数值分析、统计学、机器学习等领域中非常常见。下面是一些常见的多项式拟合算法:
1. 最小二乘法
最小二乘法是最常用的多项式拟合方法。它通过最小化误差的平方和(即残差平方和)来找到最佳的拟合多项式。具体步骤如下:
选择多项式的阶数:首先,你需要决定使用多少阶的多项式来拟合数据。阶数越高,多项式可能越能精确地通过每个数据点,但也可能导致过拟合。
建立方程组:对于给定的数据点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) (x_1,y_1),(x_2,y_2),…,(x_n,y_n) (x1,y1),(x2,y2),…,(xn,yn) 和一个 𝑚 阶多项式 p ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a m x m p(x)=a_0+a_1x+a_2x^2+⋯+a_mx^m p(x)=a0+a1x+a2x2+⋯+amxm,你可以为每个数据点建立一个方程,即 p ( x i ) = y i p(x_i)=y_i p(xi)=yi。然而,由于数据点通常不会完美地落在多项式上,你需要最小化残差 r i = p ( x i ) − y i r_i=p(x_i)−y_i ri=p(xi)−yi 的平方和。
解方程组:将残差平方和 S = ∑ i = 1 n r i 2 S=\sum_{i=1}^nr_i^2 S=∑i=1nri2最小化,通过求偏导数并令其为零,可以得到一个线性方程组,该方程组包含多项式系数 a 0 , a 1 , … , a m a_0,a_1,…,a_m a0,a1,…,am 作为未知数。
求解:解这个线性方程组,得到多项式的系数。
2. 数值方法
除了最小二乘法,还可以使用一些数值方法来求解多项式系数,如梯度下降法、牛顿法等。这些方法通过迭代地调整系数来最小化残差平方和。
3. 软件工具
在实际应用中,通常会使用专门的软件或库来执行多项式拟合,如Python的NumPy、SciPy、Matplotlib(通过NumPy的polyfit函数)或MATLAB的polyfit函数等。这些工具提供了方便的函数和接口,让用户可以轻松地拟合多项式并获取系数。
示例(Python)
使用NumPy的polyfit函数进行多项式拟合的示例:
import numpy as np
import matplotlib.pyplot as plt# 示例数据
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1])# 拟合2阶多项式
coefficients = np.polyfit(x, y, 2)
polynomial = np.poly1d(coefficients)# 打印多项式系数
print(polynomial)# 绘制原始数据点和拟合曲线
xp = np.linspace(0, 5, 100)
plt.plot(x, y, 'o', xp, polynomial(xp), '-')
plt.show()
这段代码将拟合一个2阶多项式,并绘制原始数据点和拟合的曲线。
点的多项式算法python实现样例
下面是一个Python实现的多项式算法示例:
class Polynomial:def __init__(self, coefficients):self.coefficients = coefficientsdef __str__(self):terms = []degree = len(self.coefficients) - 1for i, coeff in enumerate(self.coefficients):if coeff != 0:if i < degree:terms.append(f"{coeff}x^{degree-i}")else:terms.append(str(coeff))return ' + '.join(terms)def __add__(self, other):if len(self.coefficients) > len(other.coefficients):longer = selfshorter = otherelse:longer = othershorter = selfresult = []for i in range(len(longer.coefficients)):if i < len(shorter.coefficients):result.append(longer.coefficients[i] + shorter.coefficients[i])else:result.append(longer.coefficients[i])return Polynomial(result)def __sub__(self, other):neg_other = Polynomial([-coeff for coeff in other.coefficients])return self.__add__(neg_other)def __mul__(self, other):result = [0] * (len(self.coefficients) + len(other.coefficients) - 1)for i in range(len(self.coefficients)):for j in range(len(other.coefficients)):result[i+j] += self.coefficients[i] * other.coefficients[j]return Polynomial(result)def evaluate(self, x):result = 0for i, coeff in enumerate(self.coefficients):result += coeff * (x ** (len(self.coefficients) - i - 1))return result# 示例用法
poly1 = Polynomial([1, 0, 2]) # 2x^2 + 1
poly2 = Polynomial([3, -1]) # -x + 3add_result = poly1 + poly2
sub_result = poly1 - poly2
mul_result = poly1 * poly2print(f"poly1: {poly1}") # 输出:poly1: 2x^2 + 1
print(f"poly2: {poly2}") # 输出:poly2: -x + 3
print(f"poly1 + poly2: {add_result}") # 输出:poly1 + poly2: 2x^2 - x + 4
print(f"poly1 - poly2: {sub_result}") # 输出:poly1 - poly2: 2x^2 + x - 2
print(f"poly1 * poly2: {mul_result}") # 输出:poly1 * poly2: -3x^3 + 6x^2 - x + 3print(f"poly1(2): {poly1.evaluate(2)}") # 输出:poly1(2): 9
这个示例中,Polynomial类实现了多项式的基本操作,包括加法、减法、乘法和求值。coefficients变量存储多项式的系数。__str__方法将多项式转换为可读字符串形式。__add__、__sub__和__mul__方法实现了多项式的加法、减法和乘法。evaluate方法用于求多项式在给定值下的结果。
示例使用了两个多项式poly1和poly2进行加法、减法和乘法操作,并计算了poly1在x=2处的值。
输出结果为:
poly1: 2x^2 + 1
poly2: -x + 3
poly1 + poly2: 2x^2 - x + 4
poly1 - poly2: 2x^2 + x - 2
poly1 * poly2: -3x^3 + 6x^2 - x + 3
poly1(2): 9
相关文章:

python 实现点的多项式算法
点的多项式算法介绍 点的多项式算法通常指的是通过一组点(即数据点,通常包括自变量和因变量的值)来拟合一个多项式函数的方法。这种方法在数值分析、统计学、机器学习等领域中非常常见。下面是一些常见的多项式拟合算法: 1. 最小…...
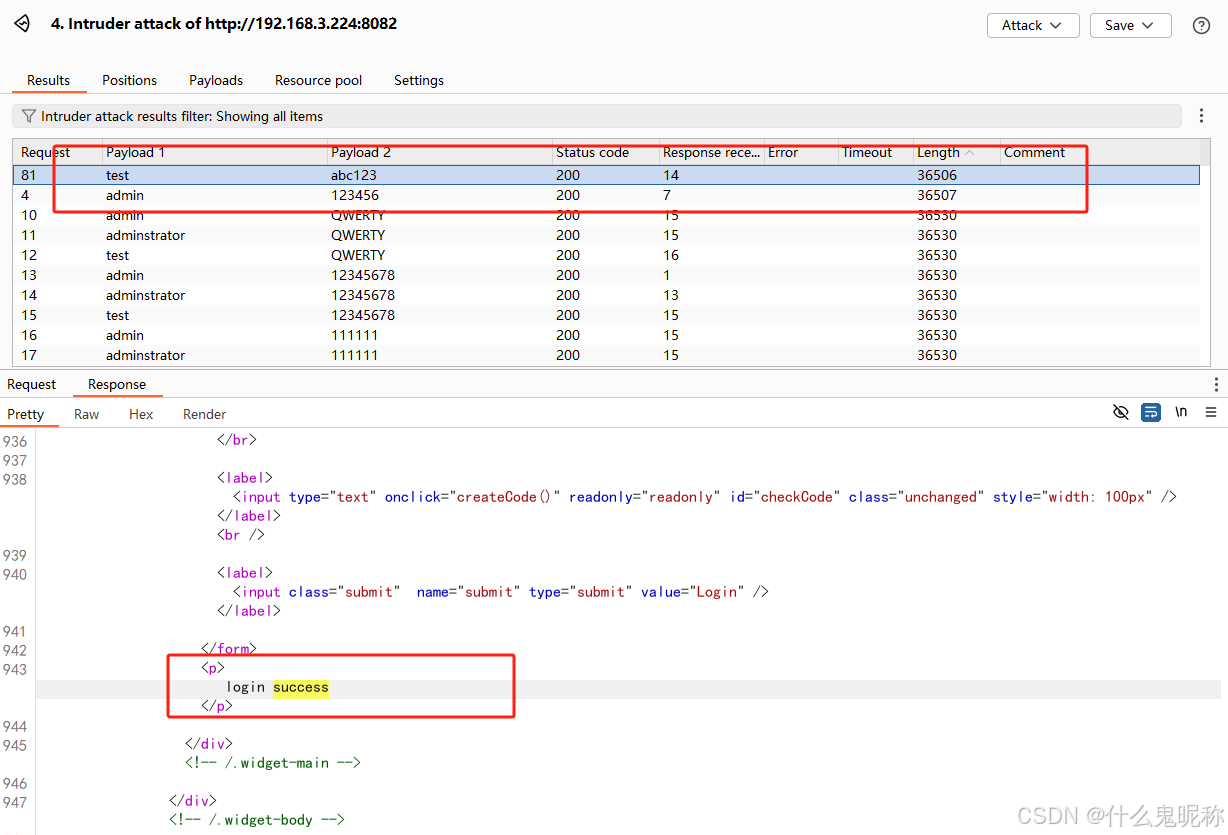
Pikachu-暴力破解-验证码绕过(on client)
访问页面, 从burpsuite 上看到返回的源代码; 验证码生成时通过 createCode 方法生成,在前端页面生成; 同时也是在前端做的校验; 直接验证;F12 -- 网络,随便输入个账号、密码、验证码࿰…...

【Spring】Bean 的生命周期:从实例化到销毁
实例化阶段: Bean的实例化是通过反射创建的。Spring根据Component、Bean或者XML中的<bean>元素配置,来确定要创建的Bean。 属性赋值阶段: 实例化完成后,Spring会进行依赖注入。包括将属性值注入到Bean的字段中,…...
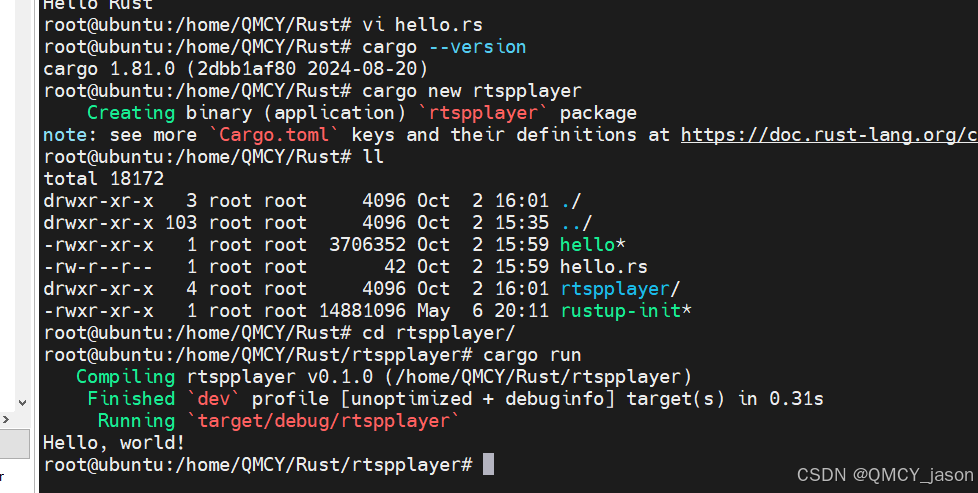
Ubuntu 安装RUST
官方给的是这样如下脚本 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh 太慢了 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh -x 执行这个脚本后会给出对应的下载链接 如下图 我直接给出来 大多数应该都是这个 https://static.rust-…...

Android Compose的基本使用
前言: Compose这个东西呢,好处我没发现,坏处就是学习成本和低版本兼容. 不过,看在官方力推的份儿上,有空就学一下吧. 当初的kotlin,很多人说鸡肋(包括我)!现在不也咔咔用纯kotlin做项目吗?哈哈哈哈. 未来的事情,谁说得清呢? 首先创建一个专用的Compose项目 对没错!看到E…...
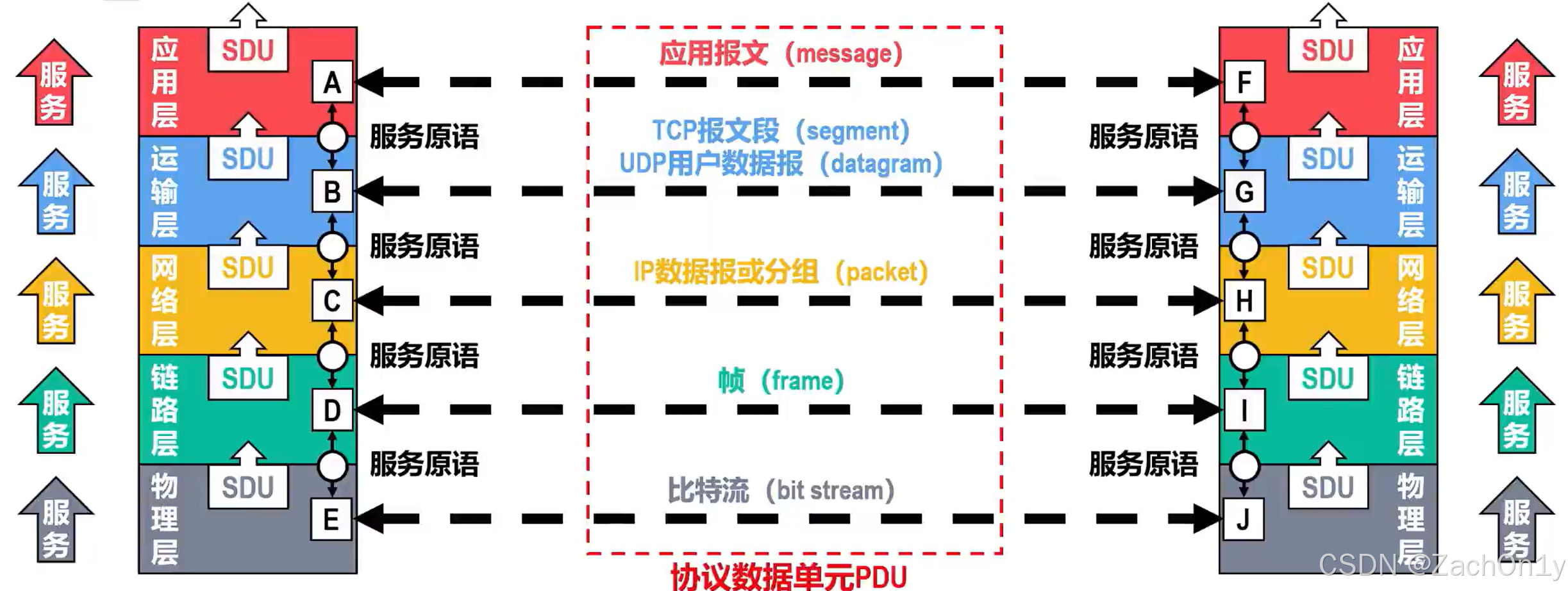
计算机网络:计算机网络体系结构 —— 专用术语总结
文章目录 专用术语实体协议服务服务访问点 SAP 服务原语 SP 协议数据单元 PDU服务数据单元 SDU 专用术语 实体 实体是指任何可以发送或接收信息的硬件或软件进程 对等实体是指通信双方处于相同层次中的实体,如通信双方应用层的浏览器进程和 Web 服务器进程。 协…...
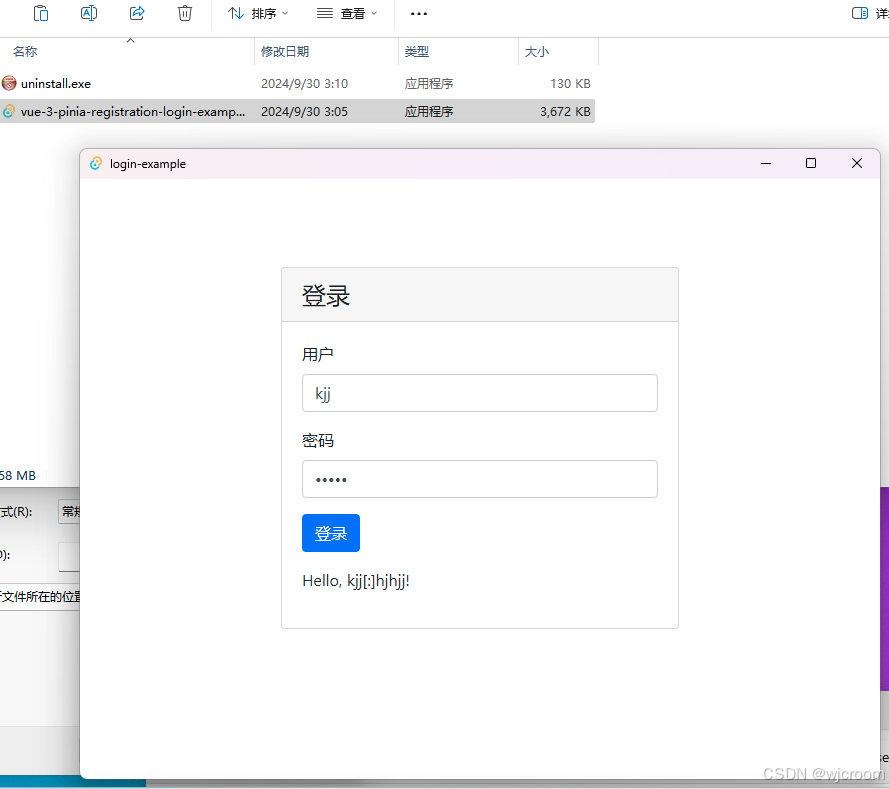
Rust的前端Tauri编程-基于JS框架的初步探索
上次的项目做完后,有一项遗憾,没有返回结果,而结果是一个html表格,我想用html直接在窗口显示,这时发现R里面包括slint没有很直接的方法,直接弹出浏览器有点太简单没有挑战。这是就被推送了他的竞争对手&…...
【Flume Kafaka实战】Using Kafka with Flume
一 目标 在Cloudera Manager中创建两个Flume的Agent,Agent1从local file中获取内容,写入到kafka的队列中。Agent2以Agent1的sink作为source,将数据从kafka中读取出来,写入到HDFS中。 二 实战 2.1 Kafka Sink 第一步࿰…...
5G NR物理信号
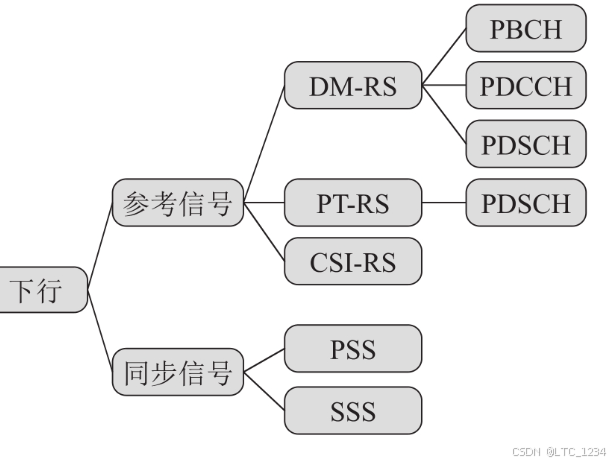
文章目录 NR 物理信号与LTE的区别上行参考信号DMRS (UL)SRSPT-RS(UL) 下行参考信号DMRS(DL)PT-RS(DL)CSI-RSPSSSSS NR 物理信号与LTE的区别 用SSS、CSI-RS和DMRS 取代了CRS信号。下行业务信道采用TM1波束赋形传输模式。基于SSB 或者CSI-RS进行RSRP和SINR测量。基于DMRS 进行共…...
Pikachu-Cross-Site Scripting-存储型xss
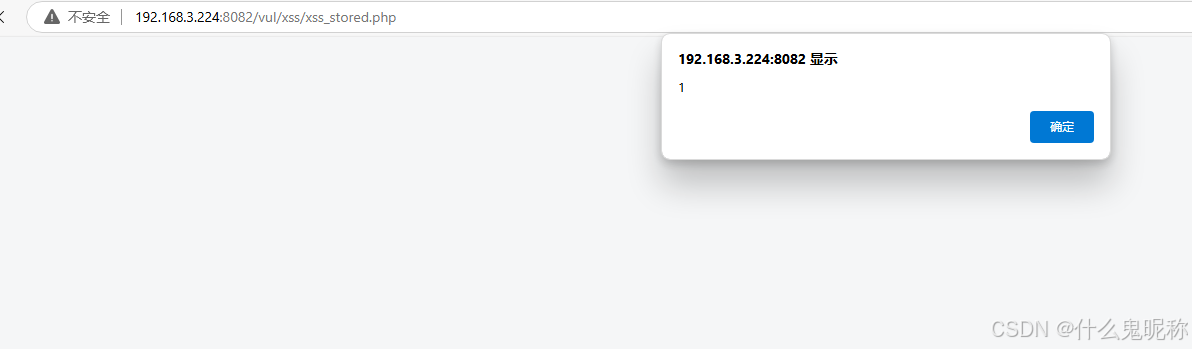
存储型xss ,随便输入点内容,都能保存下来;刷新后也不会丢失;输入特殊字符,也能原样返回; 查看代码,也可以看到输出结果直接原路返回,不做处理 构造payload <script>alert(1)…...
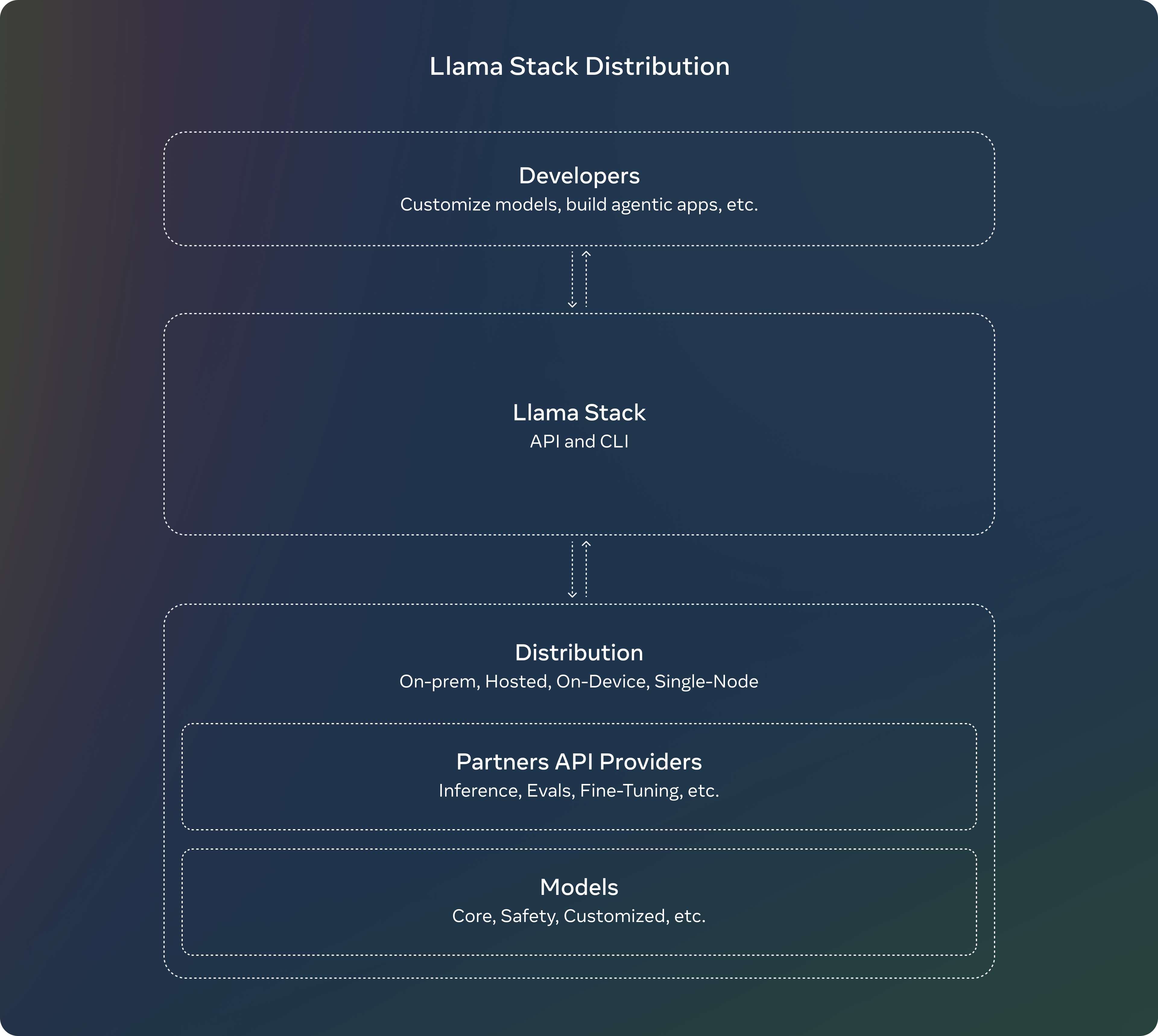
媲美GPT-4o mini的小模型,Meta Llama 3.2模型全面解读!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,专注于分享AI全维度知识,包括但不限于AI科普,AI工…...

【leetcode】 45.跳跃游戏 ||
如果我们「贪心」地进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。 例如,对于数组 [2,3,1,2,4,2,3],初始位置是下标 0,从下标 0 出发,最远可到达下标 2。下标 0 可到达的…...
、yolo(txt)、voc(xml)标注格式的相互转换)
coco(json)、yolo(txt)、voc(xml)标注格式的相互转换
一般都是用labeleme进行标注 标注格式都是json 然后根据不同的格式进行数据标注转换: 1.逐个json转xml: 当我们在使用数据集训练计算机视觉模型时,常常会遇到有的数据集只给了单个的json annotation文件,而模型所需要的annotation是基于每…...
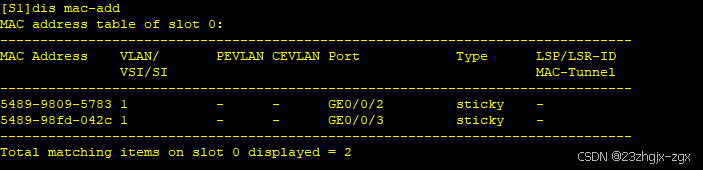
以太网交换安全:端口安全
一、端口安全介绍 端口安全是一种网络设备防护措施,通过将接口学习到的动态MAC地址转换为安全MAC地址(包括安全动态MAC和Sticky MAC),阻止除安全MAC和静态MAC之外的主机通过本接口和设备通信,从而增强设备的安全性。以…...
[题解] Codeforces Round 976 (Div. 2) A ~ E
A. Find Minimum Operations 签到. void solve() {int n, k;cin >> n >> k;if (k 1) {cout << n << endl;return;}int ans 0;while (n) {ans n % k;n / k;}cout << ans << endl; }B. Brightness Begins 打表发现, 翻转完后的序列为: 0…...
【零基础入门产品经理】学习准备篇 | 需要学一些什么呢?
前言: 零实习转行产品经理经验分享01-学习准备篇_哔哩哔哩_bilibili 该篇内容主要是对bilibili这个视频的观后笔记~谢谢美丽滴up主友情分享。 全文摘要:如何在0实习且没有任何产品相关经验下,如何上岸产品经理~ 目录 一、想清楚为什么…...

第四届机器人、自动化与智能控制国际会议(ICRAIC 2024)征稿
第四届机器人、自动化与智能控制国际会议(ICRAIC 2024)由湖南第一师范学院主办,南京师范大学、山东女子学院、爱迩思出版社(ELSP)协办。 大会将专注于机器人、数字化、自动化、人工智能等技术的开发和融合,…...
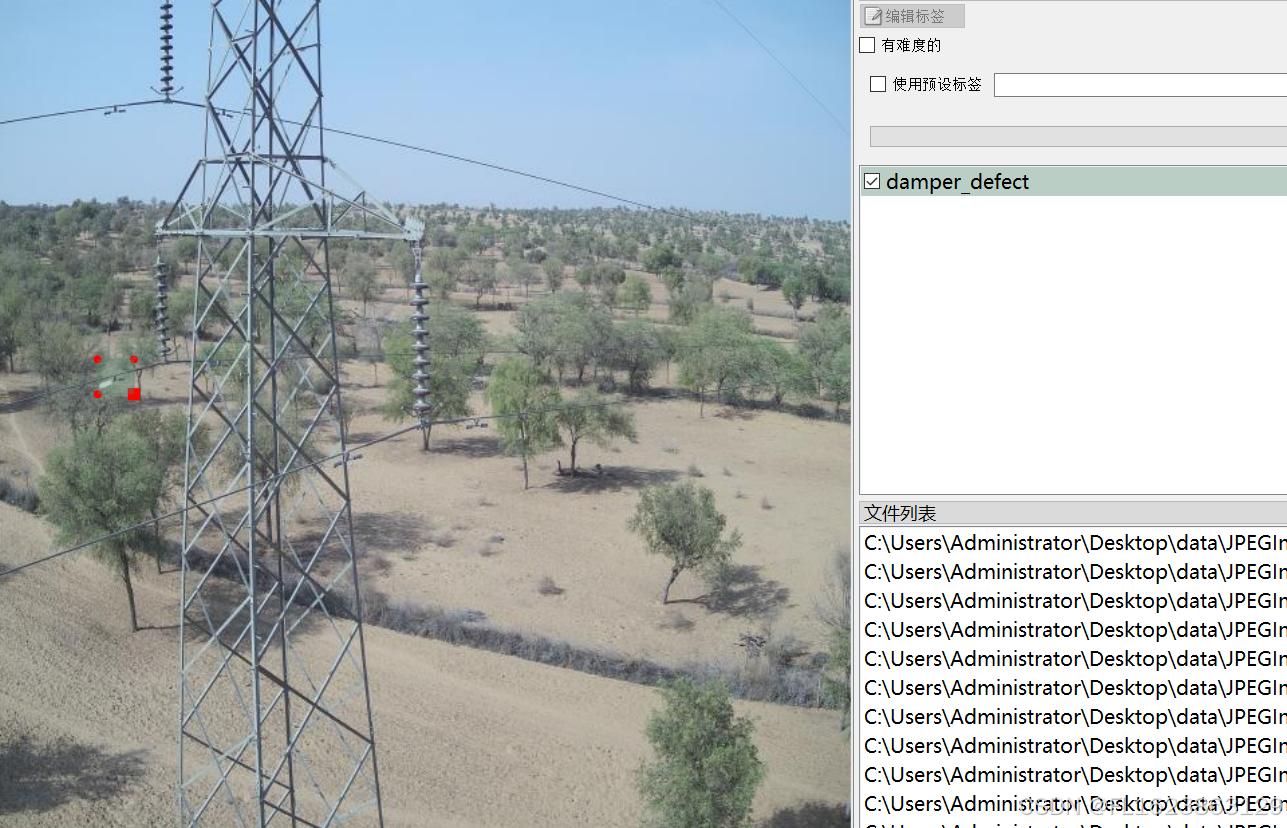
[数据集][目标检测]电力场景防震锤缺陷检测数据集VOC+YOLO格式705张1类别
重要说明:防震锤缺陷图片太难找,数据集里面存在大量单一场景图片,请仔细查看图片预览谨慎下载,此外数据集均为小目标检测,如果训练map偏低属于正常现象 数据集格式:Pascal VOC格式YOLO格式(不包含分割路径…...

【SpringBoot】
目录 一、Spring Boot概要 1. SpringBoot介绍 2. SpringBoot优点 3. SpringBoot缺点 4. 时代背景-微服务 二、Spring Boot 核心配置 1. Spring Boot配置文件分类 1.1 application.properties 1.2 application.yml 1.3 小结 2. YAML概述 3. YAML基础语法 3.1 注意事…...
Linux操作系统中MongoDB
1、什么是MongoDB 1、非关系型数据库 NoSQL,泛指非关系型的数据库。随着互联网web2.0网站的兴起,传统的关系数据库在处理web2.0网站,特别是超大规模和高并发的SNS类型的web2.0纯动态网站已经显得力不从心,出现了很多难以克服的问…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
