LeetCode题练习与总结:丑数--263
一、题目描述
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:n = 6 输出:true 解释:6 = 2 × 3
示例 2:
输入:n = 1
输出:true
解释:1 没有质因数,因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。
示例 3:
输入:n = 14 输出:false 解释:14 不是丑数,因为它包含了另外一个质因数 7 。
提示:
-2^31 <= n <= 2^31 - 1
二、解题思路
- 首先判断 n 是否为正整数,如果不是,则直接返回 false。
- 不断将 n 除以 2、3、5,直到 n 不能被这三个数整除为止。
- 如果最后 n 等于 1,则说明 n 只包含质因数 2、3、5,返回 true;否则,返回 false。
三、具体代码
class Solution {public boolean isUgly(int n) {// 判断 n 是否为正整数if (n <= 0) {return false;}// 不断将 n 除以 2、3、5,直到 n 不能被这三个数整除为止for (int factor : new int[]{2, 3, 5}) {while (n % factor == 0) {n /= factor;}}// 如果最后 n 等于 1,则返回 true;否则,返回 falsereturn n == 1;}
}
以上代码中,我们首先判断 n 是否为正整数,然后使用一个 for 循环和一个 while 循环来不断将 n 除以 2、3、5。如果最后 n 等于 1,则说明 n 只包含质因数 2、3、5,返回 true;否则,返回 false。
四、时间复杂度和空间复杂度
1. 时间复杂度
代码中的主要操作是循环除以 2、3、5,直到 n 不能被这三个数整除为止。假设 n 的质因数分解为 n = 2^a x 3^b x 5^c x d,其中 d 是除了 2、3、5 以外的质因数(如果有的话)。
- 第一个循环,当 n 能被 2 整除时,n 会除以 2,直到 n 不能被 2 整除。这需要最多 a 次操作。
- 第二个循环,当 n 能被 3 整除时,n 会除以 3,直到 n 不能被 3 整除。这需要最多 b 次操作。
- 第三个循环,当 n 能被 5 整除时,n 会除以 5,直到 n 不能被 5 整除。这需要最多 c 次操作。
因此,总的操作次数是 a + b + c,即 n 中 2、3、5 的质因数个数之和。在最坏的情况下,n 是 2、3、5 的幂,那么 a、b、c 可以达到 log_2(n)、log_3(n)、log_5(n)的数量级。因此,时间复杂度可以表示为 O(log_2(n) + log_3(n) + log_5(n))。由于对数函数的增长速度远低于线性函数,我们可以简化时间复杂度为 O(log n)。
2. 空间复杂度
代码中使用的额外空间主要是常数空间,即用于存储质因数 2、3、5 的数组。这个数组的大小是固定的,不随输入 n 的大小而变化。因此,空间复杂度为 O(1)。
五、总结知识点
-
类定义:
class Solution:定义了一个名为Solution的类。
-
方法定义:
public boolean isUgly(int n):定义了一个名为isUgly的公共方法,它接受一个整数参数n并返回一个布尔值。
-
条件判断:
if (n <= 0):使用了if语句来检查n是否小于或等于 0,用于判断n是否为正整数。
-
循环结构:
for (int factor : new int[]{2, 3, 5}):使用了增强型for循环(也称为“for-each”循环)来遍历一个整数数组,该数组包含质因数 2、3、5。
-
数学运算:
%:取模运算符,用于判断一个数是否能被另一个数整除。/=:除法赋值运算符,用于将一个数除以另一个数,并将结果赋值给原数。
-
逻辑运算:
while (n % factor == 0):while循环用于在n能被factor整除的情况下重复执行循环体内的代码。
-
返回值:
return false;和return n == 1;:根据条件返回布尔值true或false。
-
数组初始化:
new int[]{2, 3, 5}:使用数组初始化语法创建并初始化一个整数数组。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:丑数--263
一、题目描述 丑数 就是只包含质因数 2、3 和 5 的正整数。 给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。 示例 1: 输入:n 6 输出:true 解释࿱…...
)
初识C语言(五)
前言 本文章就代表C语言介绍以及了解正式完成,后续进行具体分析和详细解析学习。知识根深蒂固才可以应付后来的学习,地基要打好,后续才会轻松。 十四、结构体 结构体是C语言中最最重要的知识点,使得C语言有能力描述复杂的类型。 …...

Linux:深入理解冯诺依曼结构与操作系统
目录 1. 冯诺依曼体系结构 1.1 结构分析 1.2 存储结构分布图 2. 操作系统 2.1 概念 2.2 如何管理 2.3 什么是系统调用和库函数 1. 冯诺依曼体系结构 1.1 结构分析 不管是何种计算机,如个人笔记本电脑,服务器,都是遵循冯诺依曼结构。…...
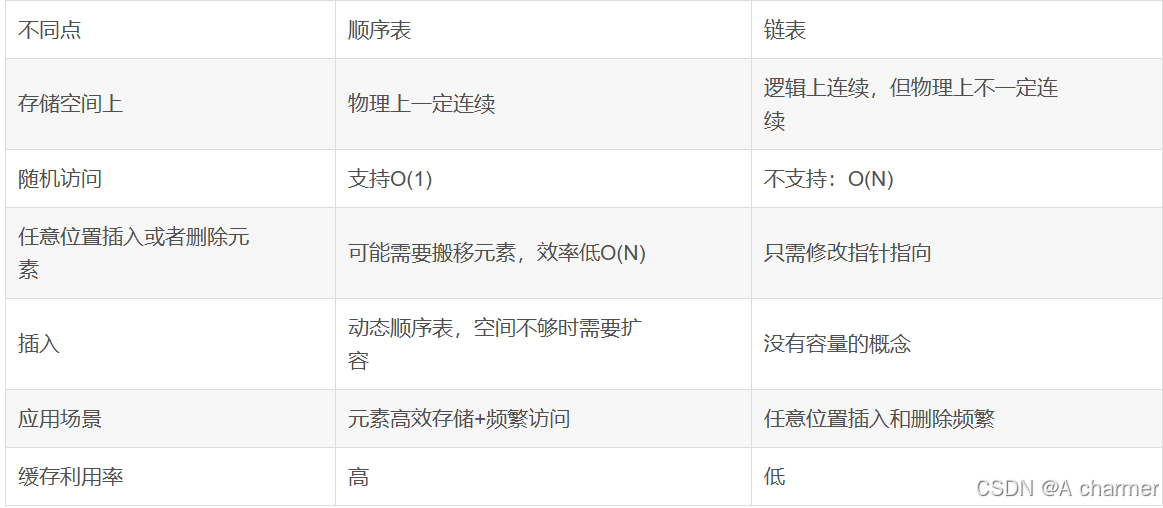
面试中顺序表常考的十大题目解析
在数据结构与算法的面试中,顺序表是一个常见的考点。它作为一种基础的数据结构,涵盖了多种操作和概念,以下将详细介绍面试中关于顺序表常考的十大题目。 💝💝💝如果你对顺序表的概念与理解还存在疑惑&#…...
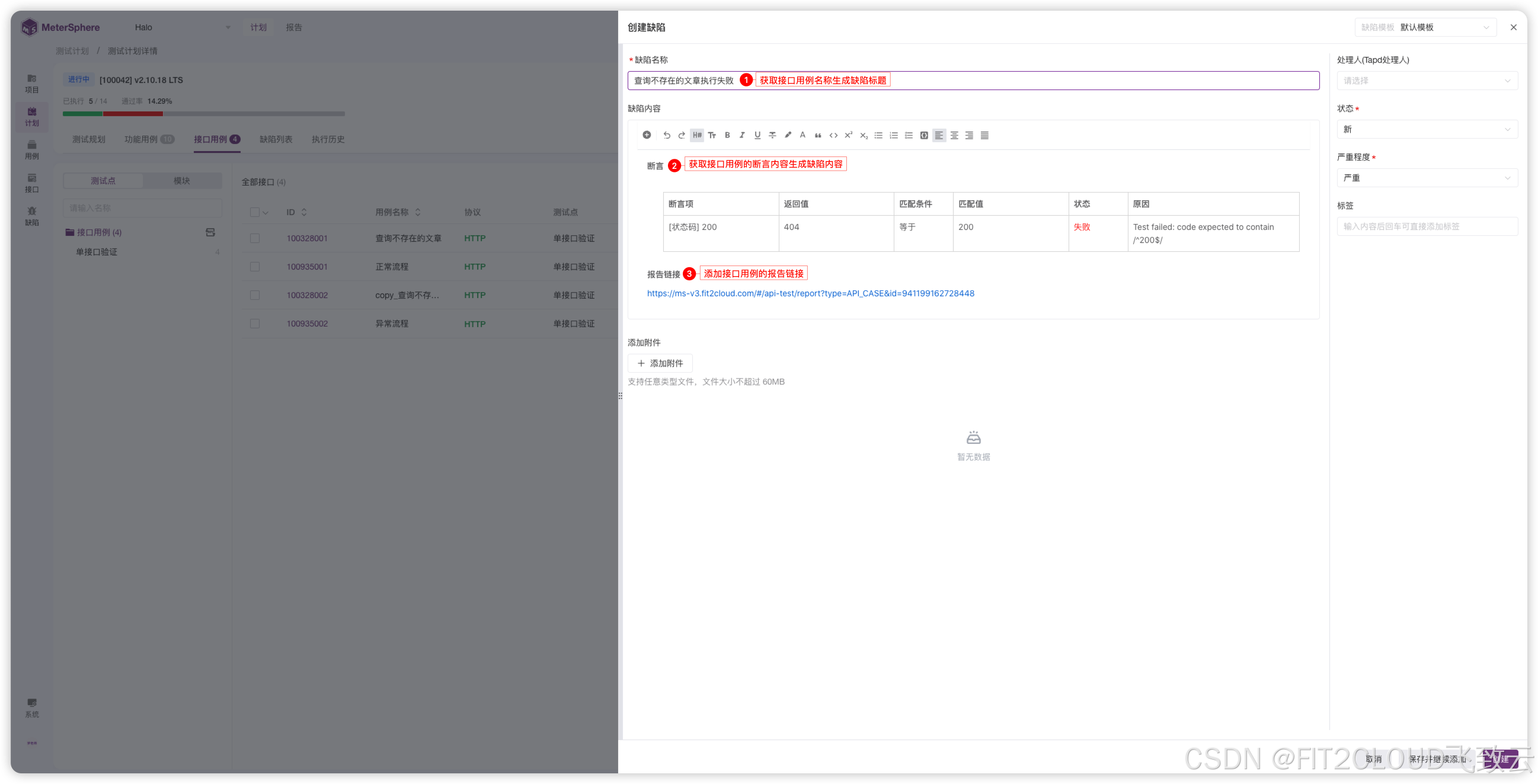
测试管理新增视图与高级搜索功能,测试计划支持一键生成缺陷详情,MeterSphere开源持续测试工具v3.3版本发布
2024年9月29日,MeterSphere开源持续测试工具正式发布v3.3版本。 在这一版本中,接口测试方面,接口导入功能支持导入Postman、JMX、HAR和MeterSphere格式的文件,接口场景的自定义请求步骤支持cURL快捷导入;测试管理方面…...
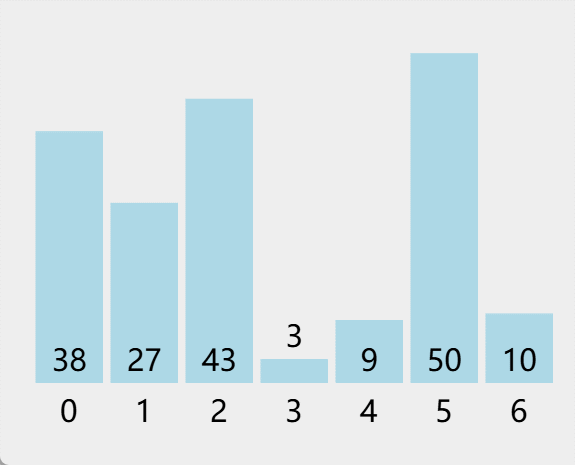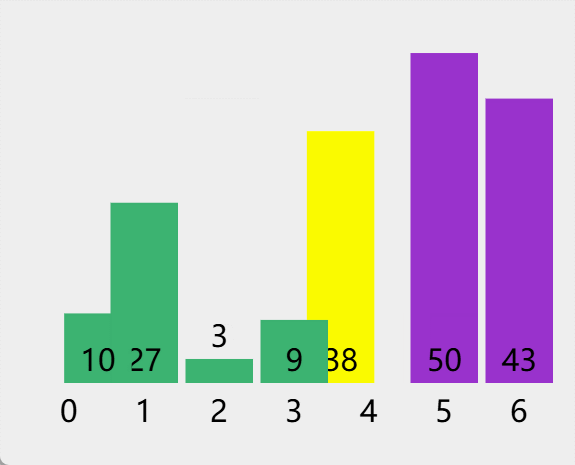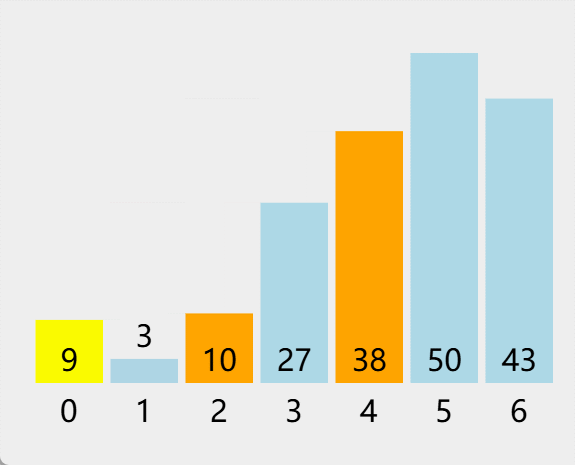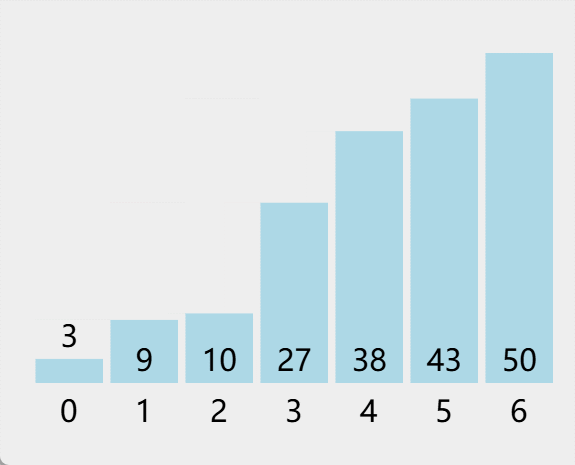
TypeScript 算法手册 【归并排序】
文章目录 1. 归并排序简介1.1 归并排序定义1.2 归并排序特点 2. 归并排序步骤过程拆解2.1 分割数组2.2 递归排序2.3 合并有序数组 3. 归并排序的优化3.1 原地归并排序3.2 混合插入排序案例代码和动态图 4. 归并排序的优点5. 归并排序的缺点总结 【 已更新完 TypeScript 设计模式…...

生信名词|MOA|基因敲低与基因敲除|DMSO|MODZ|生信基础
生信名词|MOA|基因敲低与基因敲除|DMSO|MODZ|生信基础 MOA(Mechanisms Of Action,作用机理) 过去,在药物投入到临床使用之前,它的生物学机理往往未被研究透彻。如今,随着技术的发展,一种新药物…...
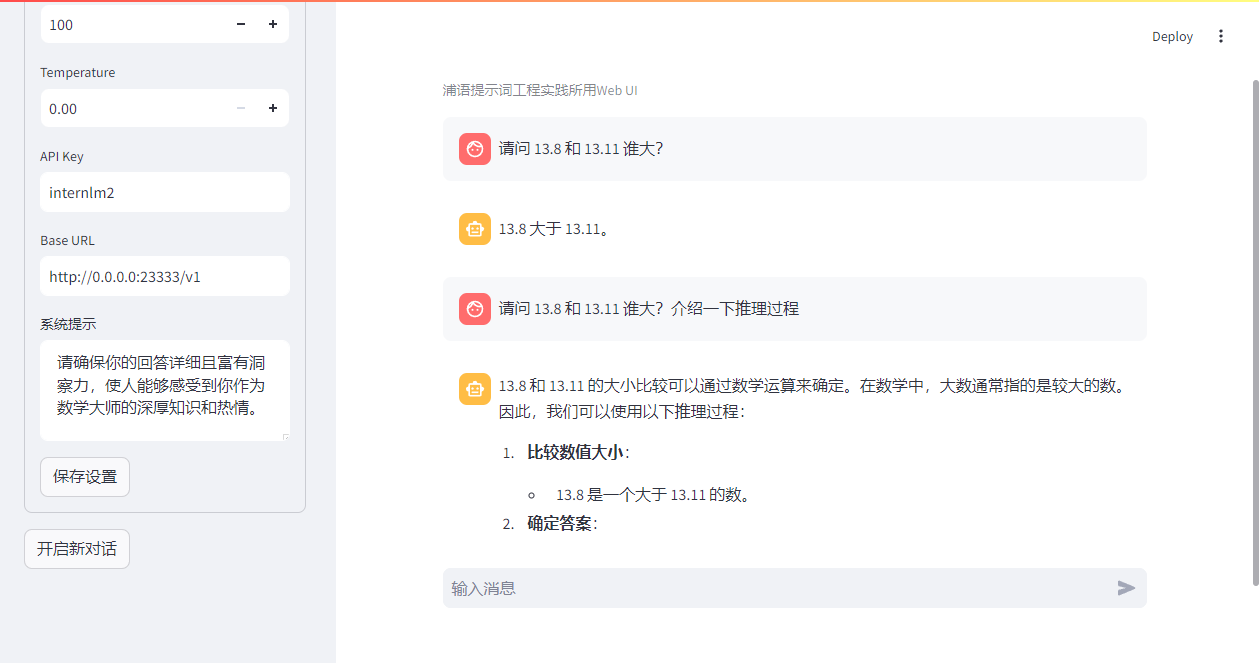
基础岛第3关:浦语提示词工程实践
模型部署 使用下面脚本测试模型 from huggingface_hub import login, snapshot_download import osos.environ[HF_ENDPOINT] https://hf-mirror.comlogin(token“your_access_token")models ["internlm/internlm2-chat-1_8b"]for model in models:try:snapsh…...
vscode中配置python虚拟环境
python虚拟环境作用 Python虚拟环境允许你为每个独立的项目创建一个隔离的环境,这样每个项目都可以拥有自己的一套Python安装包和依赖,不会互相影响。实际使用中,可以在vscode或pycharm中使用虚拟环境。 1.创建虚拟环境的方法: …...

chatGPT对我学术写作的三种帮助
chatGPT对我学术写作的三种帮助 概述提高学术写作水平大模型选择概述上下文以提供精确的指令 提升同行评审优化编辑反馈 概述 从生成式人工智能中获得的价值并非来自于技术本身盲目地输出文本,而是来自于与工具的互动,并利用自身的专业知识来完善它所生…...

【PostgreSQL 】入门篇——支持的各种数据类型介绍,包括整数、浮点数、字符串、日期、JSON、数组等
1. 整数类型 1.1 SMALLINT 描述:用于存储小范围的整数值。大小:2 字节范围:-32,768 到 32,767使用场景:适合存储小型计数器、状态码等。示例: CREATE TABLE status_codes (id SMALLINT PRIMARY KEY,description TEX…...
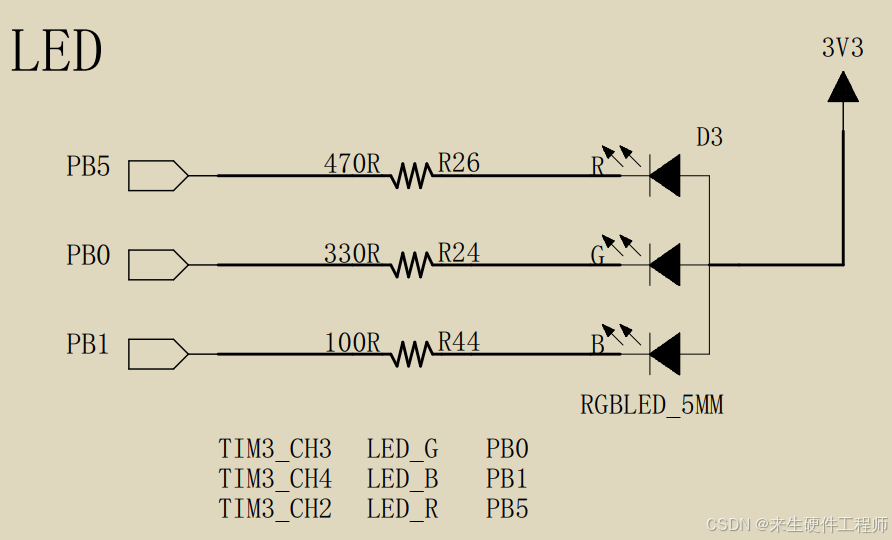
野火STM32F103VET6指南者开发板入门笔记:【1】点亮RGB
硬件介绍 提示:本文是基于野火STM32F103指南者开发板所写例程,其他开发板请自行移植到自己的工程项目当中即可。 RGB-LEDPin引脚:低电平-点亮,高电平-熄灭REDPB5GREENPB0BLUEPB1 文章目录 硬件介绍软件介绍:结构体方式…...
)
数据工程师岗位常见面试问题-3(附回答)
数据工程师已成为科技行业最重要的角色之一,是组织构建数据基础设施的骨干。随着企业越来越依赖数据驱动的决策,对成熟数据工程师的需求会不断上升。如果您正在准备数据工程师面试,那么应该掌握常见的数据工程师面试问题:包括工作…...
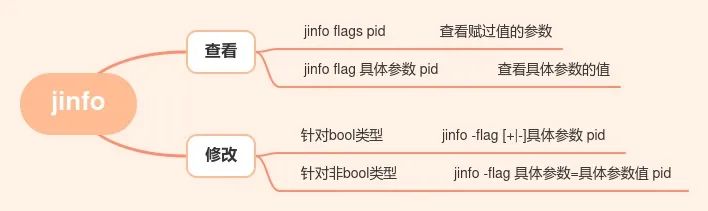
强大的JVM监控工具
介绍 在生产环境中,经常会遇到各种各样奇葩的性能问题,所以掌握最基本的JVM命令行监控工具还是很有必要的 名称主要作用jps查看正在运行的Java进程jstack打印线程快照jmap导出堆内存映像文件jstat查看jvm统计信息jinfo实时查看和修改jvm配置参数jhat用…...

python 实现点的多项式算法
点的多项式算法介绍 点的多项式算法通常指的是通过一组点(即数据点,通常包括自变量和因变量的值)来拟合一个多项式函数的方法。这种方法在数值分析、统计学、机器学习等领域中非常常见。下面是一些常见的多项式拟合算法: 1. 最小…...
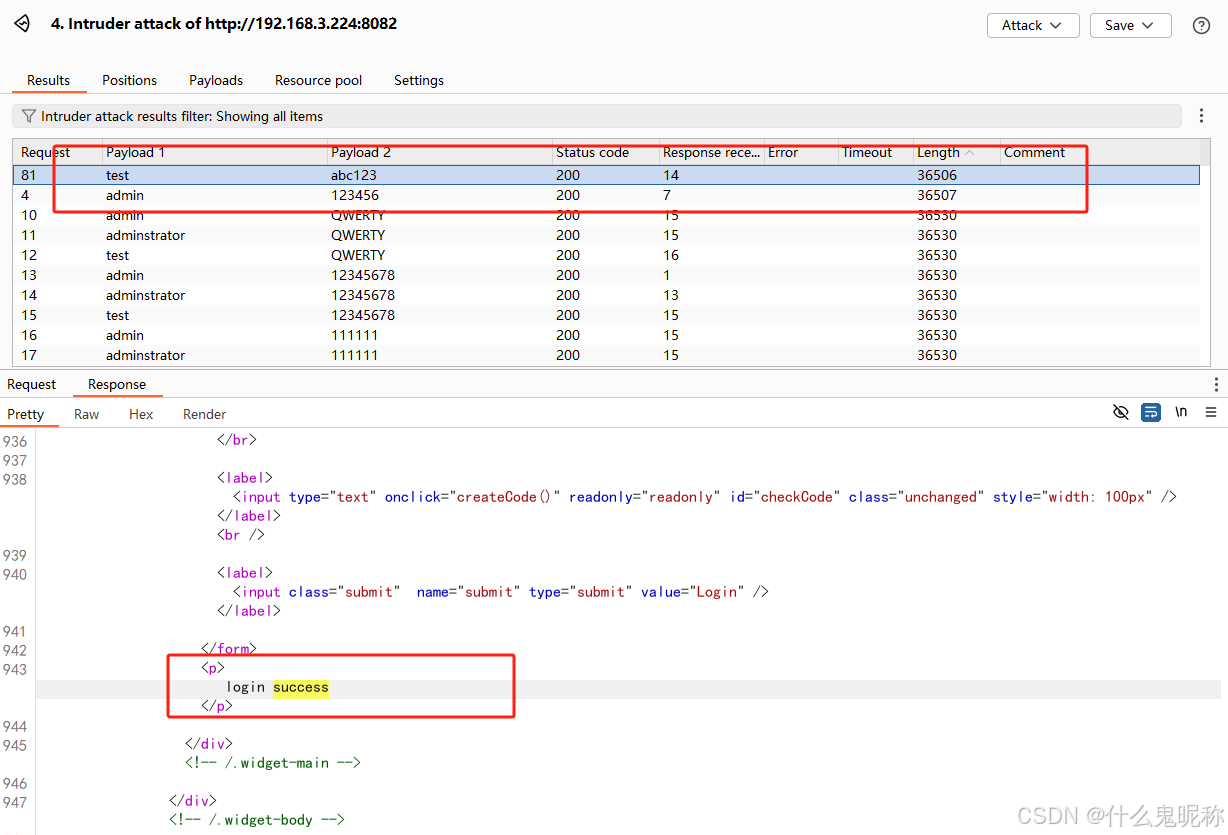
Pikachu-暴力破解-验证码绕过(on client)
访问页面, 从burpsuite 上看到返回的源代码; 验证码生成时通过 createCode 方法生成,在前端页面生成; 同时也是在前端做的校验; 直接验证;F12 -- 网络,随便输入个账号、密码、验证码࿰…...

【Spring】Bean 的生命周期:从实例化到销毁
实例化阶段: Bean的实例化是通过反射创建的。Spring根据Component、Bean或者XML中的<bean>元素配置,来确定要创建的Bean。 属性赋值阶段: 实例化完成后,Spring会进行依赖注入。包括将属性值注入到Bean的字段中,…...
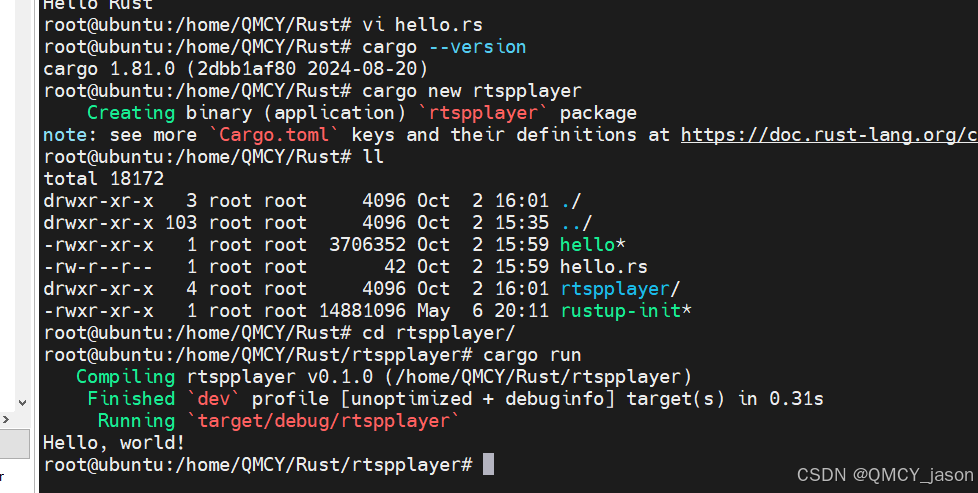
Ubuntu 安装RUST
官方给的是这样如下脚本 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh 太慢了 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh -x 执行这个脚本后会给出对应的下载链接 如下图 我直接给出来 大多数应该都是这个 https://static.rust-…...

Android Compose的基本使用
前言: Compose这个东西呢,好处我没发现,坏处就是学习成本和低版本兼容. 不过,看在官方力推的份儿上,有空就学一下吧. 当初的kotlin,很多人说鸡肋(包括我)!现在不也咔咔用纯kotlin做项目吗?哈哈哈哈. 未来的事情,谁说得清呢? 首先创建一个专用的Compose项目 对没错!看到E…...
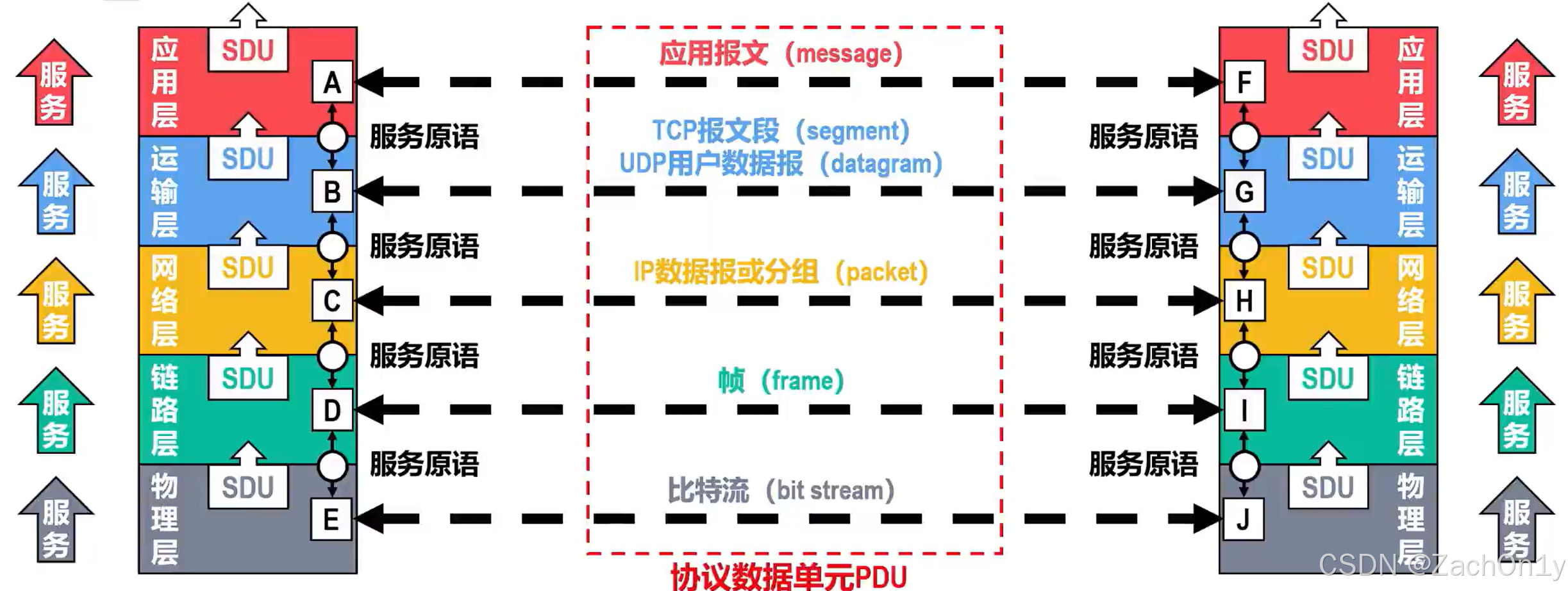
计算机网络:计算机网络体系结构 —— 专用术语总结
文章目录 专用术语实体协议服务服务访问点 SAP 服务原语 SP 协议数据单元 PDU服务数据单元 SDU 专用术语 实体 实体是指任何可以发送或接收信息的硬件或软件进程 对等实体是指通信双方处于相同层次中的实体,如通信双方应用层的浏览器进程和 Web 服务器进程。 协…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
