分布式理论:拜占庭将军问题
分布式理论:拜占庭将军问题
- 介绍
- 拜占庭将军的故事
- 将军的难题
- 解决方案
- 口信消息型拜占庭问题之解
- 流程
- 总结
- 签名消息型拜占庭问题之解
- 总结
介绍
拜占庭将军问题是对分布式共识问题的一种情景化描述,由兰伯特于1082首次发表《The Byzantine Generals Problem》中提及,它是分布式领域最复杂的一个容错模型, 它描述了如何在存在恶意行为的情况下使分布式系统达成一致,了解拜占庭问题对于掌握分布式共识问题具有深刻意义。
拜占庭将军的故事
拜占庭帝国的几只军队此时驻扎在敌人的城墙之外,每个军队都有专门的将军来指挥,但因为各只军队分别驻扎在敌城的不同地方,将军之间只能通过信使来相互联系。再某天观察完敌情之后,将军们决定制定一个共同的作战计划,同时进攻或者撤退,因为敌人非常强大,至少有半数的军队同时发动进攻时才能取得胜利。此时,将军们遇到了难题:如何统一大家的作战计划?
将军的难题
首先,如果将军之间都是忠诚于拜占庭帝国的,那么很容易统一作战方案,只需要所有的将军之间彼此通信交换自己的意见(进攻还是撤退),最后所有的将军根据 少数服从多数 的原则来行动。
这里假设只有三支军队A, B, C, 其中 A, B 认为应该进攻,C认为应该撤退,将军之间的通信如下:
通过协商,所有的将军最后的行为都是统一的进攻,于是大破敌城!
但是,如果有将军私通敌国,发送误导性的信息这样的共识协商还能保证作战计划统一吗?答案无疑是否定的,假设现在B将领是叛将,故意给A,C发送不一样的信息,情况会发生改变:
A看到的是,撤退:进攻 = 1 :2
C看到的是,撤退:进攻 = 2 :1
接下来,按照少数服从多数的原则,A会独自发动进攻,当然,最后会因为寡不敌众而被敌军消灭。可以看到,叛将通过发送误导信息,非常轻易的干扰了其他将军的作战计划,导致忠于拜占庭帝国的将军被逐一击败,这就是著名的两忠一叛难题。忠诚的将军该如何统一作战计划呢?
解决方案
兰伯特的论文除了提出拜占庭将军之外,也给出了两种解决拜占庭将军问题的算法
- 口信消息型解决方案
- 签名消息型解决方案
接下来,我会分别介绍这两种做法,如果你觉得逻辑有点绕的话,建议找张纸比划比划。
口信消息型拜占庭问题之解
口信型拜占庭之解的核心是选择出一个指挥官和进行多轮信息协商。下面来介绍具体的协商流程:
流程
首先,我们假设现在有A, B, C, D四位将军,并且其中只有D为叛将。在这个解法之中,我们首先要选择出一个将军作为指挥官,其他的将军作为副将,这里我们先让忠诚的将领A作为指挥官,与先前的协商方式不同,在这个算法中,我们需要进行2次作战协商,接下来来看两次协商的流程:
第一轮:由指挥官向所有的副将发送作战信息,每位副官将从指挥官处收到的信息作为自己的作战指令;
第二轮:三位副将之间进行作战信息协商,互相告知彼此指挥官发送的信息,其中,因为D是叛将,他会告诉两个将军不同的信息来误导他们
可以发现,虽然叛将像先前一样向两个将军发送了不同的信息,但是B,C根据少数服从多数的原则,依旧可以做出和A一样的作战行为,最后大破敌军。
也许你会想,如果指挥官是叛将呢?情况会变回糟糕吗?答案是否定的,即使指挥官是叛将,所有的忠诚的将军依然可以统一作战行为,我们假设叛将D作为指挥官先发送作战信息, 他会发送误导的错误信息,试图让其中一位将领独自发动进攻:
在第二轮的作战信息协商中,三位忠诚的副将彼此之间互通指挥官发送的消息:
最终,所有的将军收到的作战信息都是"撤退,撤退,进攻",根据少数服从多数的原则,A, B, C将撤退,达成统一的行为,保证了作战计划的一致性。
总结
这个算法虽然可以保证无论叛将如何捣乱,我们都能做出一行的行为,但是这是有前提的。在兰伯特的论文中指出:如果叛将人数为m,将军人数不能少于3m+1,只有这样,口信型拜占庭将军之解才能生效。或者说,这个算法对于能容忍的叛将数m是已知的,而且m决定了要执行多少次作战协商,即 m + 1 轮(现在你知道为什么三忠一叛的场景中为什么我们要进行两次作战协商了)。该结论具体的推导,可以参考论文。
但是我们还是没能解决两忠一叛的问题,因为忠诚的将军数量不够,此时就可以考虑第二种拜占庭问题的解法了。
签名消息型拜占庭问题之解
签名消息型拜占庭问题之解的核心是信息要格外实现以下两个特性
- 将军的签名信息无法伪造,对其签名信息的内容进行任何的修改都会被发现
- 任何将军都能能力验证将军签名信息的真伪
这样,两忠一叛难题就能够被解决了,在这种算法下,需要指挥官首先发动作战协商,然后其余的将军彼此交换指挥官带来的消息。我们以A, B 为忠诚将军,C为叛将来推导解释:
首先假设A为首先发送信息的指挥官:
因为将军的签名信息的伪造会被发现,所以B收到C的作战请求的时候,会发现A的作战请求已经被C修改,B会执行A直接发送给他的进攻命令,大破敌军。
如果是叛将C先发送作战信息,结果也不会改变:
A, B在进行协商后会发现C给两人发送的作战信息不一致,此时可以先处理叛将,再重新制定作战计划。
总结
现在让我们回到计算机世界的分布式场景中:
- 拜占庭的将军,代表着计算机节点,
- 忠诚的将军指的是正常运行的计算机节点
- 叛变的将军可以认为是出现故障,并且会发送误导信息的计算机节点
这样你是否理解了拜占庭将军问题代表的计算机分布式场景问题呢?实际上以上提到的两种算法还能解决如下的问题:信使被杀或者信使被间谍替换等。
这里强调一下,拜占庭将军问题强调的几乎是最困难也最复杂的一种分布式故障场景,计算机节点不仅存在故障,甚至还存在恶意行为,对于存在恶意节点的场景中,我们必须使用拜占庭容错算法。
相关文章:

分布式理论:拜占庭将军问题
分布式理论:拜占庭将军问题 介绍拜占庭将军的故事将军的难题 解决方案口信消息型拜占庭问题之解流程总结 签名消息型拜占庭问题之解 总结 介绍 拜占庭将军问题是对分布式共识问题的一种情景化描述,由兰伯特于1082首次发表《The Byzantine Generals Prob…...
Docker安装Nginx)
从零开始Ubuntu24.04上Docker构建自动化部署(三)Docker安装Nginx
安装nginx sudo docker pull nginx 启动nginx 宿主机创建目录 sudo mkdir -p /home/nginx/{conf,conf.d,html,logs} 先启动nginx sudo docker run -d --name mynginx -p 80:80 nginx 宿主机上拷贝docker上nginx服务上文件到本地目录 sudo docker cp mynginx:/etc/nginx/ngin…...
阿里云 SAE Web:百毫秒高弹性的实时事件中心的架构和挑战
作者:胡志广(独鳌) 背景 Serverless 应用引擎 SAE 事件中心主要面向早期的 SAE 控制台只有针对于应用维度的事件,这个事件是 K8s 原生的事件,其实绝大多数的用户并不会关心,同时也可能看不懂。而事件中心,是希望能够…...

人口普查管理系统基于VUE+SpringBoot+Spring+SpringMVC+MyBatis开发设计与实现
目录 1. 系统概述 2. 系统架构设计 3. 技术实现细节 3.1 前端实现 3.2 后端实现 3.3 数据库设计 4. 安全性设计 5. 效果展示 编辑编辑 6. 测试与部署 7. 示例代码 8. 结论与展望 一个基于 Vue Spring Boot Spring Spring MVC MyBatis 的人口普查管理…...
使用VBA快速将文本转换为Word表格
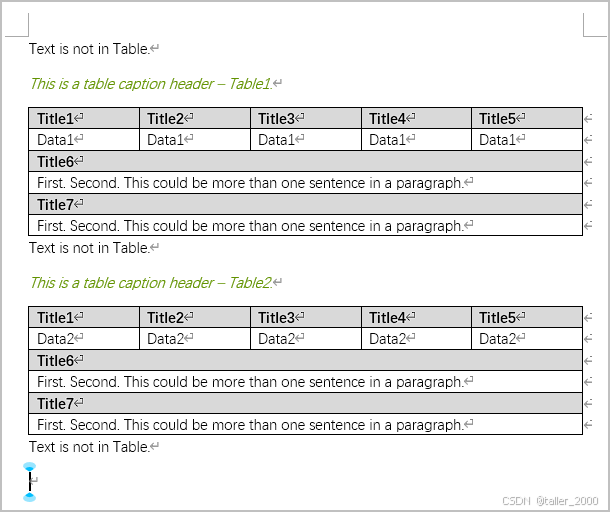
Word提供了一个强大的文本转表格的功能,结合VBA可以实现文本快速转换表格。 示例文档如下所示。 现在需要将上述文档内容转换为如下格式的表格,表格内容的起始标志为。 示例代码如下。 Sub SearchTab()Application.DefaultTableSeparator "*&quo…...

力扣题解1870
这道题是一个典型的算法题,涉及计算在限制的时间内列车速度的最小值。这是一个优化问题,通常需要使用二分查找来求解。 题目描述(中等) 准时到达的列车最小时速 给你一个浮点数 hour ,表示你到达办公室可用的总通勤时…...

D3.js数据可视化基础——基于Notepad++、IDEA前端开发
实验:D3.js数据可视化基础 1、实验名称 D3数据可视化基础 2、实验目的 熟悉D3数据可视化的使用方法。 3、实验原理 D3 的全称是(Data-Driven Documents),是一个被数据驱动的文档,其实就是一个 JavaScript 的函数库,使用它主要是用来做数据可视化的。本次实…...

在Robot Framework中Run Keyword If的用法
基本用法使用 ELSE使用 ELSE IF使用内置变量使用Python表达式本文永久更新地址: 在Robot Framework中,Run Keyword If 是一个条件执行的关键字,它允许根据某个条件来决定是否执行某个关键字。下面是 Run Keyword If 的基本用法: Run Keyword…...

虚拟机ip突然看不了了
打印大致如下: 解决办法 如果您发现虚拟机的IP地址与主机不在同一网段,可以采取的措施之一是调整网络设置。将虚拟机的网络模式更改为桥接模式,这样它就会获得与主机相同的IP地址,从而处于同一网段。或者,您可以使用…...

LeetCode[中等] 763. 划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。 返回一个表示每个字符串片段的长度的列表。 思路 贪心…...

Java LeetCode每日一题
997. 找到小镇的法官 package JavaExercise20241002;public class JavaExercise {public static void main(String[] args) {int[][] array {{1,3},{2,3},{3,1}};Solution solution new Solution();System.out.println(solution.findJudge(3, array));} }class Solution {pu…...

数据结构--集合框架
目录 1. 什么是集合框架 2. 背后所涉及的数据结构以及算法 2.1 什么是数据结构 2.2 容器背后对应的数据结构 1. 什么是集合框架 Java 集合框架 Java Collection Framework ,又被称为容器 container ,是定义在 java.util 包下的一组接口 int…...

Win10鼠标总是频繁自动失去焦点-非常有效-重启之后立竿见影
针对Win10鼠标频繁自动失去焦点的问题,可以尝试以下解决方案: 一、修改注册表(最有效的方法-重启之后立竿见影) 打开注册表编辑器: 按下WindowsR组合键,打开运行窗口。在运行窗口中输入“regedit”&#x…...

智能涌现|迎接智能时代,算力产业重构未来
前言 OpenAI首席执行官山姆奥特曼在《智能时代》中描绘了一个令人振奋的未来图景,其中算力产业将扮演至关重要的角色。奥特曼预测,我们可能在“几千天内”迎来超级智能,这一进程将极大加速社会结构的智能化转型。 这一预测与算力产业的未来…...

关于HTML 案例_个人简历展示01
案例效果展示 代码 <!DOCTYPE html> <lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>个人简历信息</title> </he…...

【前端开发入门】css快速入门
目录 引言一、css盒模型1. 盒模型概念2. 盒模型案例 二、css编写1. html文件内部编写1.1 标签style属性编写1.2 css选择器关联1.2.1 id选择器1.2.2 class选择器1.2.3 标签选择器1.2.4 css选择器作用域1.2.5 其他选择器1.2.6 各css选择器优先级 2. 单独维护css文件2.1 创建css文…...

java中创建不可变集合
一.应用场景 二.创建不可变集合的书写格式(List,Set,Map) List集合 package com.njau.d9_immutable;import java.util.Iterator; import java.util.List;/*** 创建不可变集合:List.of()方法* "张三","李四","王五…...
D25【 python 接口自动化学习】- python 基础之判断与循环
day25 for 循环 学习日期:20241002 学习目标:判断与循环﹣-35 for 循环:如何遍历一个对象里的所有元素? 学习笔记: for 循环与while循环的区别 for循环的定义 使用for循环遍历序列 使用for循环遍历字典…...

HTTP1.0和HTTP1.1有什么区别
HTTP/1.0 和 HTTP/1.1 是两个不同版本的 HTTP 协议。虽然它们的核心功能都是提供网页数据传输,但 HTTP/1.1 对 HTTP/1.0 做了很多改进,提升了性能和灵活性。以下是它们的主要区别: 1. 持久连接(Persistent Connection)…...

卡夫卡的理解
一、架构理解 在这个单聊新架构中,涉及多个服务器组件共同协作来实现单聊功能。 ChatAccessServer:可能负责处理单聊相关的访问请求,比如用户登录单聊以及发送单消息的请求接入。ChatHttpPushServer:推测其用于通过 HTTP 协议推…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
