【数据结构强化】应用题打卡
应用题打卡
数组的应用
对称矩阵的压缩存储

注意:
1.

2.上三角的行优先存储及下三角的列优先存储与数组的下表对应


上/下三角矩阵的压缩存储

注意:
上/下三角压缩存储是将0元素统一压缩存储,而不是将对角线元素统一压缩存储



三对角矩阵的压缩


栈、队列的应用
栈的定义和基本操作实现

①顺序栈

②链栈

③双向链栈



队列的定义和基本操作实现

①顺序存储的队列:注意队首尾指针进1的公式

②链式存储的队列:注意链式存储的队列出队操作

树的应用
二叉树的性质
![]()
知识点:




题目:
1.


2.


二叉树的顺序存储和基本操作

①注意二叉树的顺序存储的定义


②注意二叉树判空

数组下标从1开始存储

数组下标从0开始存储

树的性质
![]()
1.树的基本性质

5.1.4
1.


5.4.4
1.


2.


树/森林的定义和画图

①双亲表示法:森林也可以用树的双亲表示法



②孩子表示法



注:

③对比:树的孩子表示法存储 v.s. 图的邻接表存储 v.s. 散列表的拉链法 v.s. 基数排序。你发现了什么?
(1)孩子表示法

(2)图的邻接表存储


(3)散列表的拉链法

(4)基数排序



④自己动手创造,画一个结点总数不少于10的树/森林,并画出对应的“双亲表示法、孩子表示法、孩子兄弟表示法”三种数据结构的示意图
注意孩子兄弟表示法,是纯链表表示,不像孩子表示法是顺序存储+链式存储


哈夫曼树的应用


并查集的应用

3.5.1~3.5.3 实现并查集的数据结构定义,并实现 Union、Find 两个基本操作

并查操作优化:


3.5.4 设计一个例子,对10个元素 Union
记住Union操作是小树并大树,如果两个集合大小相等,则右边并入左边的树


3.5.5 基于上述例子,进行若干次 Find,并完成“压缩路径”


二叉排序树、平衡二叉树的应用题潜在考法

①计算ASL(注意需要除以结点个数)

②二叉排序树的删除
注意结点z如果只有一棵左子树或右子树,则直接让z的子树称为z父结点的子树,替代z的位置

③自己设计一个例子,给出不少于10个关键字序列,按顺序插入一棵初始为空的平衡二叉树,画出每一次插入后的样子(你设计的例子要涵盖LL、RR、LR、RL四种调整平衡的情况)
例:从一棵初始为空的AVL Trees 开始,依次插入:50、26、10(LL)、3、5(LR)、60、90(RR)、40、55、100、59(RL)

最后插入59

二叉平衡树的插入:

总结:
LL单旋:如果A结点的平衡因子绝对值大于1,就将A结点左子树根结点右旋
RR单旋:如果A结点的平衡因子绝对值大于1,就将A结点右子树根结点左旋
LR单旋:如果A结点的平衡因子绝对值大于1,就将A结点左孩子的右子树根结点先左旋再右旋
RL单旋:如果A结点的平衡因子绝对值大于1,就将A结点右孩子的左子树根结点先右旋再左旋
图的应用
图的性质

1.

2.

3.

4.

5.


图的数据结构定义

①顺序存储和链式存储的图



②带权无向图和带权有向图的邻接矩阵和邻接表表示


图的应用:最小生成树

①

②prim算法和kruskal算法


图的应用:最短路径


图的应用:拓扑排序






图的应用:关键路径

略
查找算法

分块查找



折半查找
略
散列查找
线性再探法


散列表计算,ASL成功的分母是元素总个数,ASL失败的分母是mod的那个数

来自群u的解答:

拉链法


排序算法

希尔排序

堆排序
建堆规则:

自己设计一个长度不小于10的乱序数组,用堆排序,最终要生成升序数组,画出建堆后的状态
假设乱序数组的初始状态如下,元素从0开始存储👇:

若顺序二叉树从数组下标1开始存储结点,则:
● 结点 i 的父结点编号为 i/2
● 结点 i 的左孩子编号为 i*2
● 结点 i 的右孩子编号为 i*2+1
若顺序二叉树从数组下标0开始存储结点,则:
● 结点 i 的父结点编号为 [(i+1)/2] - 1
● 结点 i 的左孩子编号为 [(i+1)*2] - 1 = 2*i + 1
● 结点 i 的右孩子编号为 [(i+1)*2+1] - 1 = 2*i + 2
在本例中,元素从数组下标0开始存储,因此,0号元素是根节点,1号元素是其左孩子,2号元素是其右孩子。其他元素间的关系如下:

由于最终要生成升序数组,因此需要建立大根堆,从最后一个分支(即6号结点)开始调整,即依次调整结点 6、5、4、3、2、1、0。建立好的大根堆如下:

注:如果应用题让你画出一个乱序数组建堆后的样子,只需要画出数组形式的图示即可,不用画二叉树形态的图示。如下👇

画出每一轮堆排序的状态














快速排序
自己设计一个长度不小于10的乱序数组,用快速排序,最终要生成升序数组
画出每一轮快速排序的状态

基数排序
略
外部排序

置换选择算法


“外部排序”在历年真题中的考频不算高,因此许多考生并不重视对该考点的复习。但是2023年应用题突然深入考察了“外部排序”,让广大考生感到被偷袭,猝不及防。因此,我们需要重视这个考点。以下是历年真题中,涉及到“外部排序”的题目:
【2016年真题11题】(选择题)考察了“外部排序的思想”
【2019年真题11题】(选择题)考察了“最佳归并树”
【2023年真题42题】(应用题)考察了“置换-选择排序”
【2024年真题11题】(选择题)考察了“败者树”
接下来,我们将2023年真题进行改编,用于回顾外部排序的三个重要考点:①置换-选择排序,②最佳归并树,③败者树
对含有19个记录的文件进行外部排序,其关键字依次是 51, 94, 37, 92, 14, 63, 15, 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100。假设每个文件记录刚好占一个磁盘块。请回答下列问题:
1)若采用置换-选择排序生成初始归并段,工作区中能保存3 个记录,可生成几个初始归并段?各是什么?请问置换-选择排序的过程中,读、写磁盘次数分别是几次?
2)若要对几个初始归并段进行3路归并,为实现最佳归并,需要补充的虚段个数是多少?请画出最佳归并树的样子,并计算该归并树的WPL。请问归并过程中,读、写磁盘次数分别是多少次?磁盘I/O次数是多少次?
3)若要对几个初始归并段进行4路归并,为减少归并过程中关键字对比次数,需使用“败者树”。请问构造初始败者树时,需要对比几次关键字?基于构造好的败者树,每次从4个归并段中找到最小关键字所需的关键字对比次数是多少?
1)
排序过程如下表所示:
| 输出文件FO | 工作区WA | 输入文件FI |
| — | — | 51, 94, 37, 92, 14, 63, 15, 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| — | 51, 94, 37 | 92, 14, 63, 15, 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 37 | 51, 94, 92 | 14, 63, 15, 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 37, 51 | 14, 94, 92 | 63, 15, 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 37, 51, 92 | 14, 94, 63 | 15, 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 37, 51, 92, 94 | 14, 15, 63 | 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 37, 51, 92, 94# | 14, 15, 63 | 99, 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 14 | 99, 15, 63 | 48, 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 14, 15 | 99, 48, 63 | 56, 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 14, 15, 48 | 99, 56, 63 | 23, 60, 31, 17, 43, 8, 90, 166, 100 |
| 14, 15, 48, 56 | 99, 23, 63 | 60, 31, 17, 43, 8, 90, 166, 100 |
| 14, 15, 48, 56, 63 | 99, 23, 60 | 31, 17, 43, 8, 90, 166, 100 |
| 14, 15, 48, 56, 63, 99 | 31, 23, 60 | 17, 43, 8, 90, 166, 100 |
| 14, 15, 48, 56, 63, 99# | 31, 23, 60 | 17, 43, 8, 90, 166, 100 |
| 23 | 31, 17, 60 | 43, 8, 90, 166, 100 |
| 23, 31 | 43, 17, 60 | 8, 90, 166, 100 |
| 23, 31, 43 | 8, 17, 60 | 90, 166, 100 |
| 23, 31, 43, 60 | 8, 17, 90 | 166, 100 |
| 23, 31, 43, 60, 90 | 8, 17, 166 | 100 |
| 23, 31, 43, 60, 90, 166 | 8, 17, 100 | — |
| 23, 31, 43, 60, 90, 166# | 8, 17, 100 | — |
| 8 | 17, 100 | — |
| 8, 17 | 100 | — |
| 8, 17, 100 | — | — |
| 8, 17, 100# | — | — |
可生成4个归并段,分别是:
37, 51, 92, 94
14, 15, 48, 56, 63, 99
23, 31, 43, 60, 90, 166
8, 17, 100
置换-选择排序的过程中,需要读磁盘19次,写磁盘19次。因为19条文件记录(即上表所示的“输入文件FI”)初始时存储在磁盘,每条记录占一个磁盘块,进行置换-选择排序时,这19条记录需要依次读入内存中(即上表所示的“工作区WA”),再逐一写回外存(即上表所示的“输出文件FO”)。因此,整个过程需要读磁盘19次,写磁盘19次。
最佳归并树练习

2)
回顾“最佳归并树”的构造方法:

本题中,有4个初始归并段,进行3路归并,因此需要构造 3叉最佳归并树。
(初始归并段数量-1) % (k-1) = (4-1)%(3-1)=1≠0,因此需要补充 (k-1)-u = (3-1)-1=1 个虚段。
补充1个虚段后,各初始归并段的长度为:
37, 51, 92, 94——归并段①长度为4
14, 15, 48, 56, 63, 99——归并段②长度为6
23, 31, 43, 60, 90, 166——归并段③长度为6
8, 17, 100——归并段④长度为3
NULL ——归并段⑤为虚段,长度为0
最佳归并树形态如下:

WPL = 树中所有叶节点的带全路径之和 = (0+3+4)*2 + (6+6)*1 = 26
注:最佳归并树形态不唯一,但WPL一定是 26
归并过程中,读磁盘次数=WPL=26次
写磁盘次数=WPL=26次
磁盘I/O总次数=WPL*2=52次。
注:每个记录刚好占一个磁盘块,因此每读一个记录就需要一次读磁盘,每写一个记录就需要一次写磁盘。
在进行第一趟归并时,需要三个归并段中的记录依次读入磁盘、再按归并顺序依次写回磁盘。因此第一趟归并带来了 0+3+4=7 次读磁盘、以及7次写磁盘。
在进行第二趟归并时,需要将三个归并段中的记录依次读入磁盘、再按归并顺序依次写回磁盘,因此第二趟归并带来了 7+6+6 = 19 次读、以及19次写。
综上,经过两趟归并,读磁盘次数 = 7+19=26次,写磁盘次数=7+19=26次。
最佳败者树




3)
本题要求构造4路归并的败者树,因此需要对比关键字 3 次。
注:三次关键字对比如图下所示

首先分别取出4个初始归并段中的最小值,用于构造初始败者树。
第一次关键字对比:将关键字8、37进行对比。37更大,为“失败者”;8更小,为“胜利者”,晋级至下一轮对比。
第二次关键字对比:将关键字14、23进行对比。23更大,为“失败者”;14更小,为“胜利者”,晋级至下一轮对比。
第三次关键字对比:将上一层的两个“胜利者”,即关键字8、14进行对比。14更大,为“失败者”;8更小,为最终“胜利者”,也就找到了最小元素。
基于构造好的败者树,每次从4个归并段中找到最小关键字所需的关键字对比次数是2次。
举个例子,在初始败者树构造完成后,可知4个归并段中,最小元素为8(来自于最左边一个归并段)。
接下来,基于已经构造好的败者树,要继续找到剩余元素中的最小关键字,仅需进行两次关键字对比。
第一次关键字对比:将关键字17、37进行对比。37更大,为“失败者”;17更小,为“胜利者”,晋级至下一轮对比。
第二次关键字对比:将关键字14、17进行对比。17更大,为“失败者”;14更小,为最终“胜利者”,也就找到了最小元素。

注:
咸鱼认为,如果考题中考到败者树,最有可能的三个出题角度是:
①问你败者树的作用
②构造k路归并的败者树时,关键字对比次数是多少?
③基于构造好的败者树,每次从k个归并段中找到最小关键字,至多/至少需要对比关键字多少次?
下面对着三个问题进行总结:
①败者树的作用是:在进行多路归并时,减少关键字对比次数。
②构造k路归并的败者树时,需要对比关键字 k-1 次。
例如:构造7路归并的败者树时,需要对比关键字6次。
③基于构造好的败者树,每次从k个归并段中找到最小关键字 所需的关键字对比次数,取决于败者树的高度和形态。万一考到这类问题,可以先画出败者树的形态,再来分析。
k路归并的败者树,形态上是一棵具有 k 个叶子结点的完全二叉树。
例如:7路归并的败者树形态如下

总共有7个叶子结点,每个叶子对应一个归并段。
基于这棵构造好的败者树,从7个归并段中找到最小关键字,最多需要3次关键字对比;最少需要2次关键字对比。
如果本轮新关键字来自于归并段1,则只需要2次关键字对比即可找到7个归并段中的最小关键字。如下所示:

如果本轮新关键字来自于归并段2,则需要3次关键字对比才能找到7个归并段中的最小关键字。如下所示:

至此,应用题打卡结束
相关文章:

【数据结构强化】应用题打卡
应用题打卡 数组的应用 对称矩阵的压缩存储 注意: 1. 2.上三角的行优先存储及下三角的列优先存储与数组的下表对应 上/下三角矩阵的压缩存储 注意: 上/下三角压缩存储是将0元素统一压缩存储,而不是将对角线元素统一压缩存储 三对角矩阵的…...

解决 MySQL 服务无法启动:failed to restart mysql.service: unit not found
目录 前言1. 问题描述2. 问题分析3. 解决步骤3.1 检查 MySQL 服务文件3.2 备份旧的服务文件3.3 启动 MySQL 服务3.4 验证服务状态 4. 总结结语 前言 在日常使用 MySQL 数据库时,有时候可能会遇到服务无法正常启动的问题。这类问题通常出现在系统更新或者服务配置文…...

Dubbo和Http的调用有什么区别
背景 我们在项目开发中,需要进行调用外部接口时,往往使用Dubbo和Http方式都能实现远程调用。那么他们在使用上,有什么区别呢? 定位不同 一个是分布式环境下的框架,一个是通信协议。 Dubbo:是一种高性能的…...

ARM 架构、cpu
一、ARM的架构 ARM是一种基于精简指令集(RISC)的处理器架构. 1、ARM芯片特点 ARM芯片的主要特点有以下几点: 精简指令集:ARM芯片使用精简指令集,即每条指令只完成一项简单的操作,从而提高指令的执行效率…...

【React】入门Day03 —— Redux 与 React Router 核心概念及应用实例详解
1. Redux 介绍 // 创建一个简单的Redux store const { createStore } Redux;// reducer函数 function counterReducer(state { count: 0 }, action) {switch (action.type) {case INCREMENT:return { count: state.count 1 };case DECREMENT:return { count: state.count -…...

u2net网络模型训练自己数据集
单分类 下载项目源码 项目源码 准备数据集 将json转为mask json_to_dataset.py import cv2 import json import numpy as np import os import sys import globdef func(file):with open(file, moder, encoding"utf-8") as f:configs json.load(f)shapes configs…...

登录功能开发 P167重点
会话技术: cookie jwt令牌会话技术: jwt生成: Claims:jwt中的第二部分 过滤器: 拦截器: 前端无法识别controller方法,因此存在Dispa什么的...
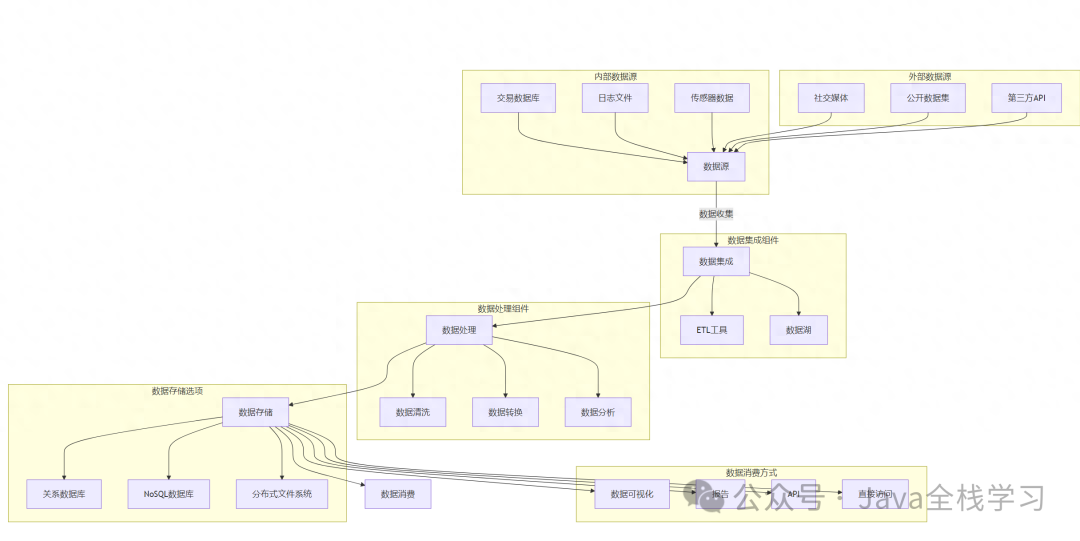
数据架构图:从数据源到数据消费的全面展示
在这篇文章中,我们将探讨如何通过架构图来展示数据的整个生命周期,从数据源到数据消费。下面是一个使用Mermaid格式的示例数据架构图,展示了数据从源到消费的流动、处理和存储过程。 数据架构图示例 说明 数据源:分为内部数据源&…...

useEffect 与 useLayoutEffect 的区别
useEffect 与 useLayoutEffect 的区别 useEffect和useLayoutEffect是处理副作用的React钩子函数,有以下区别1. 执行时机不同2. 对性能影响不同3. 对渲染的影响不同:4. 使用场景不同 使用建议 useEffect和useLayoutEffect是处理副作用的React钩子函数&…...
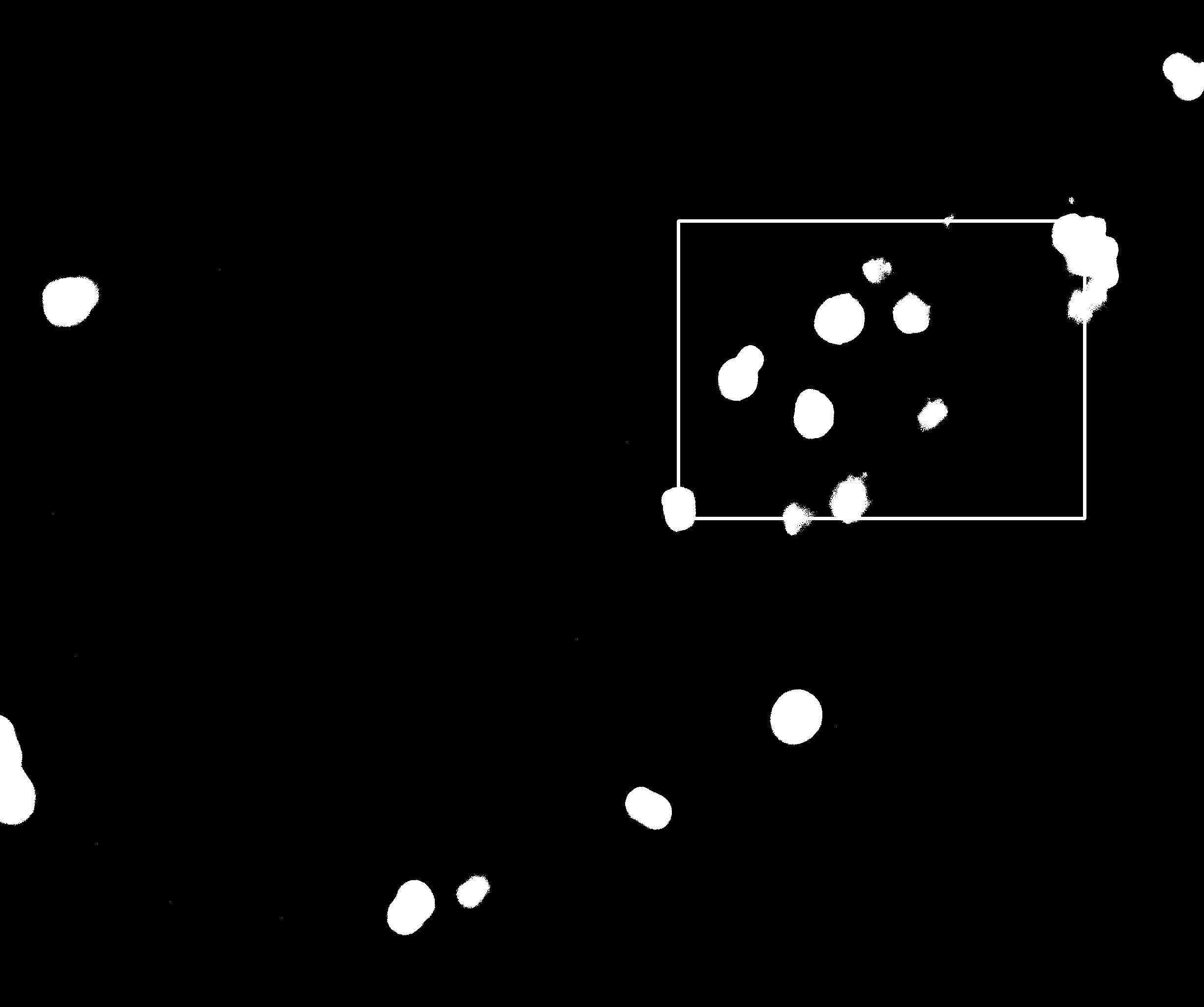
OPENCV判断图像中目标物位置及多目标物聚类
文章目录 在最近的项目中,又碰到一个有意思的问题需要通过图像算法来解决。就是显微拍摄的到的医疗图像中,有时候目标物比较偏,也就是在图像的比较偏的位置,需要通过移动样本,将目标物置于视野正中央,然后再…...

分布式理论:拜占庭将军问题
分布式理论:拜占庭将军问题 介绍拜占庭将军的故事将军的难题 解决方案口信消息型拜占庭问题之解流程总结 签名消息型拜占庭问题之解 总结 介绍 拜占庭将军问题是对分布式共识问题的一种情景化描述,由兰伯特于1082首次发表《The Byzantine Generals Prob…...
Docker安装Nginx)
从零开始Ubuntu24.04上Docker构建自动化部署(三)Docker安装Nginx
安装nginx sudo docker pull nginx 启动nginx 宿主机创建目录 sudo mkdir -p /home/nginx/{conf,conf.d,html,logs} 先启动nginx sudo docker run -d --name mynginx -p 80:80 nginx 宿主机上拷贝docker上nginx服务上文件到本地目录 sudo docker cp mynginx:/etc/nginx/ngin…...
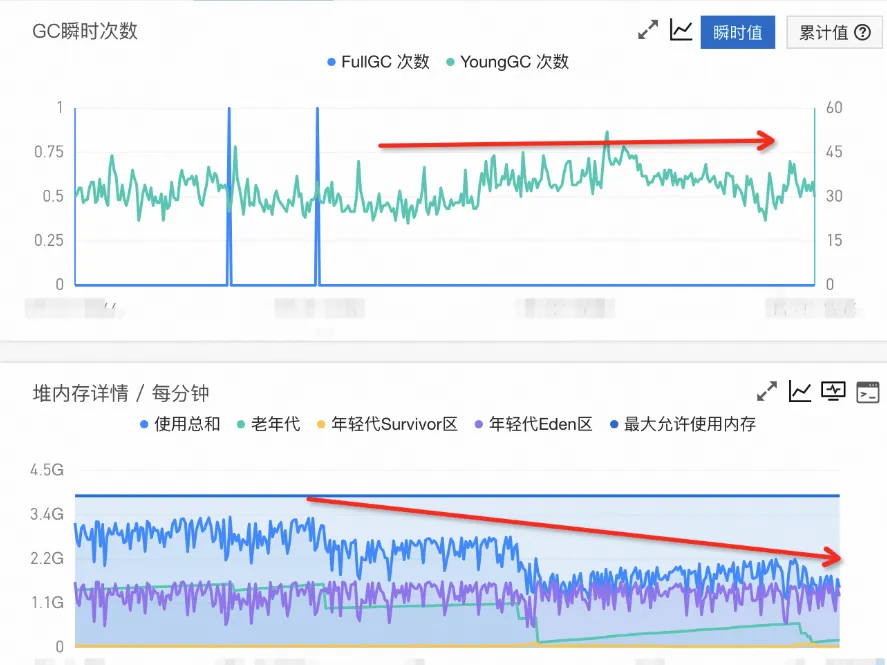
阿里云 SAE Web:百毫秒高弹性的实时事件中心的架构和挑战
作者:胡志广(独鳌) 背景 Serverless 应用引擎 SAE 事件中心主要面向早期的 SAE 控制台只有针对于应用维度的事件,这个事件是 K8s 原生的事件,其实绝大多数的用户并不会关心,同时也可能看不懂。而事件中心,是希望能够…...

人口普查管理系统基于VUE+SpringBoot+Spring+SpringMVC+MyBatis开发设计与实现
目录 1. 系统概述 2. 系统架构设计 3. 技术实现细节 3.1 前端实现 3.2 后端实现 3.3 数据库设计 4. 安全性设计 5. 效果展示 编辑编辑 6. 测试与部署 7. 示例代码 8. 结论与展望 一个基于 Vue Spring Boot Spring Spring MVC MyBatis 的人口普查管理…...
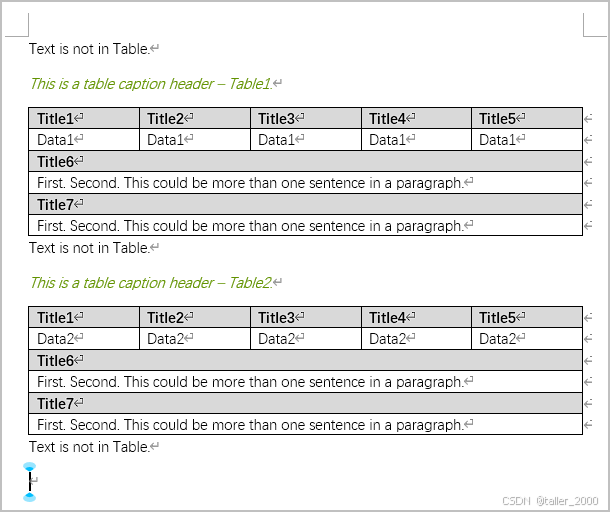
使用VBA快速将文本转换为Word表格
Word提供了一个强大的文本转表格的功能,结合VBA可以实现文本快速转换表格。 示例文档如下所示。 现在需要将上述文档内容转换为如下格式的表格,表格内容的起始标志为。 示例代码如下。 Sub SearchTab()Application.DefaultTableSeparator "*&quo…...

力扣题解1870
这道题是一个典型的算法题,涉及计算在限制的时间内列车速度的最小值。这是一个优化问题,通常需要使用二分查找来求解。 题目描述(中等) 准时到达的列车最小时速 给你一个浮点数 hour ,表示你到达办公室可用的总通勤时…...

D3.js数据可视化基础——基于Notepad++、IDEA前端开发
实验:D3.js数据可视化基础 1、实验名称 D3数据可视化基础 2、实验目的 熟悉D3数据可视化的使用方法。 3、实验原理 D3 的全称是(Data-Driven Documents),是一个被数据驱动的文档,其实就是一个 JavaScript 的函数库,使用它主要是用来做数据可视化的。本次实…...

在Robot Framework中Run Keyword If的用法
基本用法使用 ELSE使用 ELSE IF使用内置变量使用Python表达式本文永久更新地址: 在Robot Framework中,Run Keyword If 是一个条件执行的关键字,它允许根据某个条件来决定是否执行某个关键字。下面是 Run Keyword If 的基本用法: Run Keyword…...

虚拟机ip突然看不了了
打印大致如下: 解决办法 如果您发现虚拟机的IP地址与主机不在同一网段,可以采取的措施之一是调整网络设置。将虚拟机的网络模式更改为桥接模式,这样它就会获得与主机相同的IP地址,从而处于同一网段。或者,您可以使用…...

LeetCode[中等] 763. 划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。 返回一个表示每个字符串片段的长度的列表。 思路 贪心…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
