机器学习篇-day02-KNN算法实现鸢尾花模型和手写数字识别模型
一. KNN简介
KNN思想
K-近邻算法(K Nearest Neighbor,简称KNN)。比如:根据你的“邻居”来推断出你的类别
KNN算法思想:如果一个样本在特征空间中的k 个最相似的样本中的大多数属于某一个类别,则该样本也属于这个类别
K值根据网格和交叉验证来确定
样本相似性:样本都是属于一个任务数据集的。样本距离越近则越相似。
利用K近邻算法预测电影类型
K值的选择
KNN的应用方式
解决问题:分类问题、回归问题
算法思想
若一个样本在特征空间中的 k 个最相似的样本大多数属于某一个类别,则该样本也属于这个类别
相似性:欧氏距离
分类问题的处理流程

-
计算未知样本到每一个训练样本的距离
-
将训练样本根据距离大小升序排列
-
取出距离最近的 K 个训练样本
-
进行多数表决,统计 K 个样本中哪个类别的样本个数最多
-
将未知的样本归属到出现次数最多的类别
回归问题的处理流程

-
计算未知样本到每一个训练样本的距离
-
将训练样本根据距离大小升序排列
-
取出距离最近的 K 个训练样本
-
把这个 K 个样本的目标值计算其平均值
-
作为将未知的样本预测的值
总结
KNN概念: K Nearest Neighbor
一个样本最相似的k个样本中的大多数属于某一个类别, 则该样本也属于这个类别
KNN分类流程
-
计算未知样本到每个训练样本的距离
-
将训练样本根据距离大小升序排列
-
取出距离最近的K个训练样本
-
进行多数表决,
统计k个样本中哪个类别的样本个数最多 -
将未知的样本归属到出现次数最多的类别
KNN回归流程
-
计算未知样本到每个训练样本的距离
-
将训练样本根据距离大小升序排列
-
取出距离最近的k个样本
-
把这k个样本的目标值计算平均值 -
平均值就是这个未知样本的预测值
K值的选择
K值过小, 模型过于复杂, 造成过拟合(训练集表现很好, 测试集表现不好)
K值过大, 模型过于简单, 造成欠拟合(训练集和测试集的表现都不好)

二. KNN算法API
KNN算法介绍
概述
类似于: 近朱者赤近墨者黑
流程
-
导包.
-
创建 (分类)算法对象.
-
准备 训练集数据, 即: x_train, y_train
-
训练模型 => 机器学习.
-
模型预测(评估)
-
打印模型预测的结果.
前提
环境中已经安装了 scikit-learn 包
分类问题演示
原理
先计算样本数据 到 训练集每个记录的 欧式距离, 然后根据欧式距离升序排列, 取出最近的 K个 样本值. 然后进行 投票, 哪个分类多, 则该分类的标签, 就是: 预测值的标签.
代码演示
模块: KNeighborsClassifier
# 1. 导包.
from sklearn.neighbors import KNeighborsClassifier
# 2. 创建 (分类)算法对象.
# estimator 单词的意思是 => 估量值, 评估值...
# Neighbors 单词的意思是 => 近邻(邻居)...
# estimator = KNeighborsClassifier(n_neighbors=1) # 即: k=1, 找最近的哪个样本.
estimator = KNeighborsClassifier(n_neighbors=3) # 即: k=1, 找最近的哪个样本.
# 3. 准备 训练集数据, 即: x_train, y_train
x_train = [[0], [1], [2], [3]]
y_train = [0, 0, 1, 1] # 分类 => 2分类
# 4. 训练模型 => 机器学习.
estimator.fit(x_train, y_train) # fitting => 拟合
# 5. 模型预测(评估)
my_result = estimator.predict([[4]])
# 6. 打印模型预测的结果.
print(f'预估值: {my_result}')
注:
上述代码中的y_train= [0, 0, 0, 1]时: 输出评估结果为0
上述代码中的estimator = KNeighborsClassifier(n_neighbors=2),
y_train= [0, 0, 0, 1] 时:
输出评估结果为0(选择较为简单的模型, 此案例中类似于排序后的第一个)
回归问题演示
原理
先计算样本数据 到 训练集每个记录的 欧式距离, 然后根据欧式距离升序排列, 取出最近的 K个样本值. 然后 计算这些样本值的平均值, 将平均值作为该分类的标签, 即: 预测值的标签.
代码演示
模块: KNeighborsRegressor
# 1. 导包.
# from sklearn.neighbors import KNeighborsRegressor
# from sklearn.neighbors import KNeighborsClassifier
# from sklearn.neighbors import KNeighborsRegressor, KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
# 2. 创建 (回归)算法对象.
# 细节: 因为k值是手动传入的, 所有手动传入的值都称之为: 超参数.
estimator = KNeighborsRegressor(n_neighbors=4) # K = 3, 即: 3个样本.
# 3. 准备 训练集数据, 即: x_train, y_train
# 73 107 88 101
# 8,0,3 7,3,7 6,4,6 6,8,1
x_train = [[1, 2, 5], [2, 5, 1], [3, 6, 2], [3, 10, 7]]
y_train = [0.1, 0.2, 0.3, 0.4]
# 4. 训练模型 => 机器学习.
estimator.fit(x_train, y_train)
# 5. 模型预测(评估)
my_result = estimator.predict([[9, 2, 8]])
# 6. 打印模型预测的结果.
print(f'预测值: {my_result}')
三. 距离度量
欧式距离

曼哈顿距离-街区距离
曼哈顿城市特点: 横平竖直


举个例子:
ABCD四点 X=[ [1,1], [2,2], [3,3], [4,4] ] ,
计算AB AC AD BC BD曼哈顿距离
经计算得: AB =|2-1|+ ⌈2-1⌉= 2
d = 2 4 6 2 4 2
了解-切比雪夫距离
切比雪夫距离:
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。
国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。


举个例子:
ABCD四点 X=[ [1,1], [2,2], [3,3], [4,4] ] ,
计算AB AC AD BC BD曼哈顿距离
经计算得: AB =max(|2-1|, ⌈2-1⌉) = 1
d = 1 2 3 1 2 1
了解-闵可夫距离-闵氏距离
闵可夫斯基距离 Minkowski Distance 闵氏距离
-
不是一种新的距离的度量方式。
-
是对多个距离度量公式的概括性的表述

其中p是一个变参数:
当 p=1 时,就是曼哈顿距离;
当 p=2 时,就是欧氏距离;
当 p→∞ 时,就是切比雪夫距离。
根据 p 的不同,闵氏距离可表示某一类种的距离。

四. 特征预处理
特征的量纲(单位或者大小)相差较大, 容易影响(支配)目标结果, 使得一些模型(算法)无法学习到其他的特征.
因此进行特征预处理, 无论是标准化 还是 归一化, 目的都是对特征数据做预处理, 降低 因量纲问题(单位) 影响结果
归一化-小数据集
原理
对原始数据做处理, 获取到1个 默认[mi, mx] => [0, 1] 区间的值
公式
x' = (x - min) / (max - min)
x'' = x' * (mx - mi) + mi
公式解释
x: 某特征到的 某个具体要操作的值,牌:原值min: 该转征到的最小值max: 该特征到的最大值mi: 区间的最小值,默认是:0mx: 一区间的最大值,默认是:1
弊端
容易受到最大值和最小值的影响(如: 最大值是10001, 最小值是1, 导致最终结果都缩小10000倍)
强依赖于该特征列的 最大值和最小值,如果差值较大,计算结果可能不明显,归一化适用于 较小数据集 的特征预处理.
图解
归一化API
sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
feature_range 缩放区间
调用 fit_transform(X) 将特征进行归一化缩放
代码演示
# 导包
from sklearn.preprocessing import MinMaxScaler # 归一化的类
# 1. 准备特征数据. 每个子列表 = 1个样本(Sample)
data = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
# 2. 创建归一化对象.
transfer = MinMaxScaler()
# 3. 具体的 归一化动作.
# fit_transform(): 训练 + 转换 => 适用于 训练集.
# transform(): 直接转换 => 适用于 测试集.
new_data = transfer.fit_transform(data)
# 4. 打印 归一化后的结果
print(f'归一化后, 数据集为: {new_data}')

★标准化-大数据集
对原始数据做处理, 转换为均值为0, 标准差为1的标准正态分布序列.
原理
公式
x' = (x - mean均值) / 该列的标准差
公式解释
x: 某列特征的某个具体要操作的值, 即: 原值
mean: 该列的平均值
方差:
标准差:
应用场景
标准化适用于 大数据集的 特征预处理.
在样本数据量较大的情况下, 异常值对样本的均值和标准差的影响可以忽略不计
标准化API
sklearn.preprocessing.StandardScaler()
fit_transform(X)将特征进行归一化缩放
代码演示
# 导包
from sklearn.preprocessing import StandardScaler # 标准化的类
# 1. 准备特征数据. 每个子列表 = 1个样本(Sample)
data = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
# 2. 创建 标准化 对象.
transfer = StandardScaler()
# 3. 具体的 标准化 动作.
# fit_transform(): 训练 + 转换 => 适用于 训练集.
# transform(): 直接转换 => 适用于 测试集.
new_data = transfer.fit_transform(data)
# 4. 打印 标准化 后的结果
print(f'标准化后, 数据集为: {new_data}')
# 5. 打印每个特征列的 平均值 和 标准差
print(f'均值: {transfer.mean_}')
print(f'方差: {transfer.var_}')

总结


五. 鸢尾花案例
回归机器建模流程:
数据获取
数据基本处理(空值和非法值)
特征工程(特征提取, 特征预处理(归一化, 标准化), 特征降维, 特征选择, 特征组合)
模型训练
模型预测
模型评估
导包
# 导包 from sklearn.datasets import load_iris # 加载鸢尾花测试集的. import seaborn as sns import pandas as pd import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split # 分割训练集和测试集的 from sklearn.preprocessing import StandardScaler # 数据标准化的 from sklearn.neighbors import KNeighborsClassifier # KNN算法 分类对象 from sklearn.metrics import accuracy_score # 模型评估的, 计算模型预测的准确率
定义加载数据函数
# 1. 定义函数 dm01_load_iris(), 用于加载 鸢尾花数据集, 并简单查看下数据集的各部分. def dm01_load_iris():# 1. 加载数据集.iris_data = load_iris() # 2. 打印iris_data, 发现其实是1个: 字典.print(iris_data) # 3. 打印所有的键, 即: 属性名.# dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])print(iris_data.keys()) # 4. 查看数据集的 特征字段.print(iris_data.data[:5]) # 5. 查看数据集的 标签字段.print(iris_data.target[:5]) # [0, 0, 0, 1, 2] # 6. 查看数据集的 标签名.print(iris_data.target_names) # ['setosa' 'versicolor' 'virginica'] # 7. 查看数据集的 字段(特征)名.print(iris_data.feature_names) # ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] # 8. 查看数据集的 描述信息# print(iris_data.DESCR) # 9. 查看数据集的 文件名print(iris_data.filename) # 10. 查看数据集的 数据模型.print(iris_data.data_module)
可视化查看数据
# 2. 定义函数 dm02_show_iris(), 用于通过 Seaborn散点图的方式. 鸢尾花数据集进行可视化查看.
def dm02_show_iris():# 1. 加载 鸢尾花 数据集.iris_data = load_iris()# 2. 将上述的数据封装成df对象, 用于: 可视化展示的数据源.iris_df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)# 3. 给df对象新增1列, 表示: 标签.iris_df['label'] = iris_data.targetprint(iris_df)
# 4. 具体的可视化, 散点图.# x: x轴值, 这里是: 花瓣的长度, y: y轴值, 这里是: 花瓣的宽度, hue: 颜色(根据鸢尾花的标签来分组, 不同分组颜色不同), fit_reg=False, 不绘制拟合回归线.sns.lmplot(data=iris_df, x='petal length (cm)', y='petal width (cm)', hue='label', fit_reg=False)# 设置标题plt.title('iris data')# 绘图plt.show()
数据集划分
# 3. 定义函数 dm03_train_test_split(), 实现: 划分 训练集 和 测试集.
def dm03_train_test_split():# 1. 加载数据集.iris_data = load_iris()# 2. 具体的划分训练集 和 测试集的动作.# iris_data.data => 特征, 一共150条# iris_data.target => 标签, 一共150条# test_size => 测试集占比, 0.2 => 训练集 : 测试集 => 8 : 2# random_state => 随机种子, 如果种子一样, 则每次划分的数据集都是一样的.# 细节: 返回值的时候, 注意下四个参数的顺序, 即: 训练集特征, 测试集特征, 训练集标签, 测试集标签.x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=21)# 3. 打印划分后的结果.print(f'训练集, x-特征: {len(x_train)}')print(f'测试集, x-特征: {len(x_test)}')print(f'训练集, y-标签: {len(y_train)}')
训练和评估模型
# 4. 定义函数 dm04_模型预估和评测(), 表示: KNN算法基于鸢尾花数据集的模型预估和评测.
def dm04_模型预估评测():# 1. 加载数据.iris_data = load_iris()# 2. 数据的预处理.# 因为就150条数据, 且没有脏数据, 所以这里我们只要划分 训练集 和 测试集即可, 无需做其它的处理.x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=21)
# 3. 特征工程, 子工程(选做)为: 特征提取, 特征预处理(归一化, 标准化), 特征降维, 特征选择, 特征组合# 查看训练集的 特征, 因为特征是已经提取好的, 所以无需我们手动提取了, 即, 特征为: 花萼的长度, 花萼的宽度, 花瓣长度, 花瓣的宽度.# 要不要做特征预处理呢? 我们发现训练集的特征数据差值不大, 所以可以不用做 特征预处理, 但是我们加入这个步骤, 会让整体的代码更规范, 便于你搭建自己的编程习惯.# print(x_train)# 3.1 创建 标准化对象.transfer = StandardScaler()# 3.2 标准化 x_train => 训练集的 特征数据.# fit_transform(): 适用于首次对数据进行标准化处理的情况, 通常用于训练集, 能同时完成 fit() 和 transform()。x_train = transfer.fit_transform(x_train)# print(x_train)# 3.3 标准化 x_test => 测试集的 特征数据.# transform(): 适用于已经训练好的标准化对象, 对测试集进行标准化处理的情况。x_test = transfer.transform(x_test)
# 4. 模型训练 => 机器学习.# 4.1 创建 估计器对象 => 分类器对象.estimator = KNeighborsClassifier(n_neighbors=5)# 4.2 模型训练 => 机器学习.estimator.fit(x_train, y_train) # 训练集的特征, 训练集的标签.
# 5. 模型预测# 场景1: 对测试集做预测.y_predict = estimator.predict(x_test) # y_predict => 预测后的 测试集的 标签.print(f'(测试集)预测结果为: {y_predict}')
# 场景2: 对新数据集做预测.# step1: 定义新的数据集.my_data = [[2.1, 3.5, 5.6, 3.2]]# step2: 对新数据集进行-数据标准化.my_data = transfer.transform(my_data)# step3: 对新数据集做(结果, 分类)预测, 获取预测结果.my_predict = estimator.predict(my_data)print(f'(新数据集)预测结果为: {my_predict}')
# step4: 对新数据集做概率预测, 看看上述的新数据集在 各个标签中的预测概率.my_predict_proba = estimator.predict_proba(my_data)print(f'(新数据集)概率预测结果为: {my_predict_proba}') # [0标签的概率, 1标签的概率, 2标签的概率]
# 6. 模型评估, KNN(K近邻算法), 评估指标主要是: 预测的准确率, 即: 100个样本中的, 正确预测的个数.# 方式1: 直接评估, 获取准确率.print(f'直接评估: 准确率: {estimator.score(x_test, y_test)}') # 传入: 测试集的特征, 测试集的标签.
# 方式2: 拿着预测值 和 真实值进行对比, 得到准确率.# y_test: 测试集的 真实 标签.# y_predict: 测试集的 预估 标签.print(f'预测值和真实值对比评估, 准确率为: {accuracy_score(y_test, y_predict)}')
六. 超参数选择
自己理解:
交叉验证: 对一个参数进行不同数据集划分, 对每个划分的数据集的评分求平均值
网格搜索: 对多个超参数值进行选择, 选择出最优的参数, 即: 对每个超参数进行交叉, 求出最优解
交叉验证
交叉验证是划分数据集的一种方法, 目的是为了得到更准确可信的模型评分
图示
交叉验证是一种数据集的分割方法,将训练集划分为 n 份,其中一份做验证集、其他n-1份做训练集
交叉验证法原理
将数据集划分为 cv=10 份:
-
第一次:把第一份数据做验证集,其他数据做训练
-
第二次:把第二份数据做验证集,其他数据做训练
-
... 以此类推,总共训练10次,评估10次。
-
使用训练集+验证集多次评估模型,取平均值做交叉验证为模型得分
-
若k=5模型得分最好,再使用全部训练集(训练集+验证集) 对k=5模型再训练一边,再使用测试集对k=5模型做评估
网格搜索
网格搜索: 指的是 GridSearchCV这个工具的功能, 可以帮助我们寻找最优的 超参数.
超参数解释: 在机器学习中, 我们把需要用户手动传入的参数称之为: 超参数.
为什么需要网格搜索
-
模型有很多超参数,其能力也存在很大的差异。需要手动产生很多超参数组合,来训练模型
-
每组超参数都采用交叉验证评估,最后选出最优参数组合建立模型。
网格搜索是模型调参的有力工具。寻找最优超参数的工具
只需要将若干参数传递给网格搜索对象,它自动帮我们完成不同超参数的组合、模型训练、模型评估,最终返回一组最优的超参数。
网格搜索+交叉验证的强力组合 (模型选择和调优)
-
交叉验证解决模型的数据输入问题(数据集划分)得到更可靠的模型
-
网格搜索解决超参数的组合
-
两个组合再一起形成一个模型参数调优的解决方案
交叉验证网格搜索 API
代码演示
# 导包
from sklearn.datasets import load_iris # 加载鸢尾花测试集的.
from sklearn.model_selection import train_test_split, GridSearchCV # 分割训练集和测试集的, 网格搜索 => 找最优参数组合
from sklearn.preprocessing import StandardScaler # 数据标准化的
from sklearn.neighbors import KNeighborsClassifier # KNN算法 分类对象
from sklearn.metrics import accuracy_score # 模型评估的, 计算模型预测的准确率
# 1. 加载数据.
iris_data = load_iris()
# 2. 数据预处理, 即: 划分 训练集, 测试集.
x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=21)
# 3. 特征工程, 即: 特征的预处理 => 数据的标准化.
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train) # 训练 + 转换 => 适用于: 训练集.
x_test = transfer.transform(x_test) # 直接转换 => 适用于: 测试集.
# 4. 模型训练.
# 4.1 创建 估计器对象.
estimator = KNeighborsClassifier()
# 4.2 定义网格搜索的参数, 即: 样本可能存在的参数组合值 => 超参数.
param_dict = {'n_neighbors': [1, 2, 3, 5, 7]}
# 4.3 创建网格搜索对象, 帮我们找到最优的参数组合.
# 参1: 估计器对象, 传入1个估计器对象, 网格搜索后, 会自动返回1个功能更加强大(最优参数)的 估计器对象.
# 参2: 网格搜索的参数, 传入1个字典, 键: 参数名, 值: 参数值列表.
# 参3: 交叉验证的次数, 指定值为: 4
estimator = GridSearchCV(estimator, param_dict, cv=5)
# 4.4 调用 估计器对象的 fit方法, 完成模型训练.
estimator.fit(x_train, y_train)
# 4.5 查看网格搜索后的参数
print(f'最优组合平均分: {estimator.best_score_}')
print(f'最优估计器对象: {estimator.best_estimator_}') # 3
print(f'具体的验证过程: {estimator.cv_results_}')
print(f'最优的参数: {estimator.best_params_}')
# 5. 得到超参数最优值之后, 再次对模型进行训练.
estimator = KNeighborsClassifier(n_neighbors=3)
# 模型训练
estimator.fit(x_train, y_train)
# 模型评估
# 方式1: 直接评估
print(estimator.score(x_test, y_test)) # 0.9666666666666667
# 方式2: 比较真实值和预测值
y_predict = estimator.predict(x_test)
print(accuracy_score(y_test, y_predict)) # 0.9666666666666667
七. 图像识别案例
导包
# 导包 import matplotlib.pyplot as plt import pandas as pd from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier import joblib from collections import Counter
查看数字图片
# 1. 定义函数 show_digit(idx), 用于查看: 数字图片.
def show_digit(idx):# idx: 行索引, 即: 要哪行的数据.# 1. 读取数据, 获取df对象.data = pd.read_csv('data/手写数字识别.csv')# 细节: 非法值校验.if idx < 0 or idx > len(data) - 1 :return# 2. 获取数据, 即: 特征 + 标签x = data.iloc[:, 1:]y = data.iloc[:, 0]# 3. 查看下数据集.print(f'x的维度: {x.shape}') # (42000, 784)print(f'y的各分类数量: {Counter(y)}') # Counter({1: 4684, 7: 4401, 3: 4351, 9: 4188, 2: 4177, 6: 4137, 0: 4132, 4: 4072, 8: 4063, 5: 3795})
# 4. 获取具体的 某张图片, 即: 某行数据 => 样本数据.# step1: 把图片转成 28 * 28像素(二维数组)digit = x.iloc[idx].values.reshape(28, 28)# step2: 显示图片.plt.imshow(digit, cmap='gray') # 灰色显示 => 灰度图# step3: 取消坐标显示.plt.axis('off')# step4: 显示图片plt.show()
训练并保存模型
# 2. 定义函数 train_model(), 用于训练模型.
def train_model():# 1. 读取数据, 获取df对象.data = pd.read_csv('data/手写数字识别.csv')# 2. 获取数据, 即: 特征 + 标签x = data.iloc[:, 1:]y = data.iloc[:, 0]# 3. 数据的预处理.# step1: x轴(像素点)的 归一化处理.x = x / 255# step2: 区分训练集和测试集. stratify: 按照y的类别比例进行分割x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y, random_state=21)# 4. 训练模型.estimator = KNeighborsClassifier(n_neighbors=3)estimator.fit(x_train, y_train)# 5. 模型预估, 评测正确率.my_score = estimator.score(x_test, y_test)print(f'模型预估正确率: {my_score}') # 0.9657142857142857# 6. 保存模型.joblib.dump(estimator, 'model/knn.pth')
加载并测试模型
# 3. 定义use_model()函数, 用于: 测试模型.
def use_model(): # pytest# 1. 加载图片.img = plt.imread('data/demo.png') # 28 * 28像素plt.imshow(img, cmap='gray') # 灰度图plt.show()
# 2. 加载模型.estimator = joblib.load('model/knn.pth')
# 3. 预测图片.img = img.reshape(1, -1) # 效果等价于: reshape(1, 784)y_test = estimator.predict(img)print(f'预测的数字是: {y_test}')

相关文章:

机器学习篇-day02-KNN算法实现鸢尾花模型和手写数字识别模型
一. KNN简介 KNN思想 K-近邻算法(K Nearest Neighbor,简称KNN)。比如:根据你的“邻居”来推断出你的类别 KNN算法思想:如果一个样本在特征空间中的k 个最相似的样本中的大多数属于某一个类别,则该样本也属…...

【C++】STL--vector
1.vector的介绍 我们先来看看vector的文档介绍,实际中我们只要熟悉相关接口就好了。 成员函数 使用STL的三个境界:能用,明理,能扩展 ,那么下面学习vector,我们也是按照这个方法去学习 2 vector的使用 v…...

Java使用Redis的详细教程
Redis是一个基于内存的key-value结构数据库,即非关系型数据库,具有高性能、丰富的数据类型、持久化、高可用性和分布式等特点。在Java项目中,Redis通常用于缓存、分布式锁、计数器、消息队列和排行榜等场景。以下是在Java中使用Redis的详细教…...

严重 Zimbra RCE 漏洞遭大规模利用(CVE-2024-45519)
攻击者正在积极利用 CVE-2024-45519,这是一个严重的 Zimbra 漏洞,该漏洞允许他们在易受攻击的安装上执行任意命令。 Proofpoint 的威胁研究人员表示,攻击始于 9 月 28 日,几周前,Zimbra 开发人员发布了针对 CVE-2024-…...

php函数积累
对称函数 isset 判断数组arr中是否存在键key 返回值true/false isset(name,$arr) unset 删除数组中的键 需存在key不然抛出异常 unset($arr[name]) json_encode 数据转json格式 json_encode($arr) 一般形式 指定字符编码形式 json_decode json格式转原有数据格式 json_d…...

前端项目场景相关的面试题,包含验证码、图片存储、登录鉴权、动态路由、组件划分等项目场景实际的面试题
项目场景面试题 如何防止短信验证码被刷 问题场景 添加倒计时和图片滑动验证,避免不必要的资源浪费 发送短信验证码需要费用发送短信消耗服务器资源 公司的图片、视频、文件资源如何存储的 传统模式 分开存储到数据服务器,托管服务器到云端 缺点&…...

uniapp 上了原生的 echarts 图表插件了 兼容性还行
插件地址:echarts - DCloud 插件市场 兼容性这块儿不知道后期会不会支持其他浏览器 H5 的话建议可以用原生的不用这个插件...

共享单车轨迹数据分析:以厦门市共享单车数据为例(八)
副标题:基于POI数据的站点综合评价——以厦门市为例(三) 什么是优劣解距离法(TOPSIS)? 优劣解距离法(Technique for Order Preference by Similarity to Ideal Solution,简称TOPSI…...

sentinel原理源码分析系列(二)-动态规则和transport
本文是sentinel原理源码分析系列第二篇,分析两个组件,动态配置和transport 动态规则 Sentinel提供动态规则机制,依赖配置中心,如nacos,zookeeper,组件支持动态配置,模板类型为规则,支…...

ubuntu切换源方式记录(清华源、中科大源、阿里源)
文章目录 前言一、中科大源二、清华源三、阿里源 前言 记录ubunut切换各个源的方式。 备注:更换源之后使用sudo apt-get update更新索引。 提示:以下是本篇文章正文内容,下面案例可供参考 一、中科大源 地址:https://mirrors.u…...

【10】纯血鸿蒙HarmonyOS NEXT星河版开发0基础学习笔记-泛型基础全解(泛型函数、泛型接口、泛型类)及参数、接口补充
序言: 本文详细讲解了关于ArkTs语言中的泛型,其中包含泛型函数、泛型接口、泛型约束、泛型类及其中参数的使用方法,补充了一部分接口相关的知识,包括接口的继承和具体实现,也写到了一些边边角角的小知识,剩…...

2024年09月CCF-GESP编程能力等级认证C++编程一级真题解析
本文收录于专栏《C++等级认证CCF-GESP真题解析》,专栏总目录:点这里。订阅后可阅读专栏内所有文章。 一、单选题(每题 2 分,共 30 分) 第 1 题 据有关资料,山东大学于1972年研制成功DJL-1计算机,并于1973年投入运行,其综合性能居当时全国第三位。DJL-1计算机运算控制…...
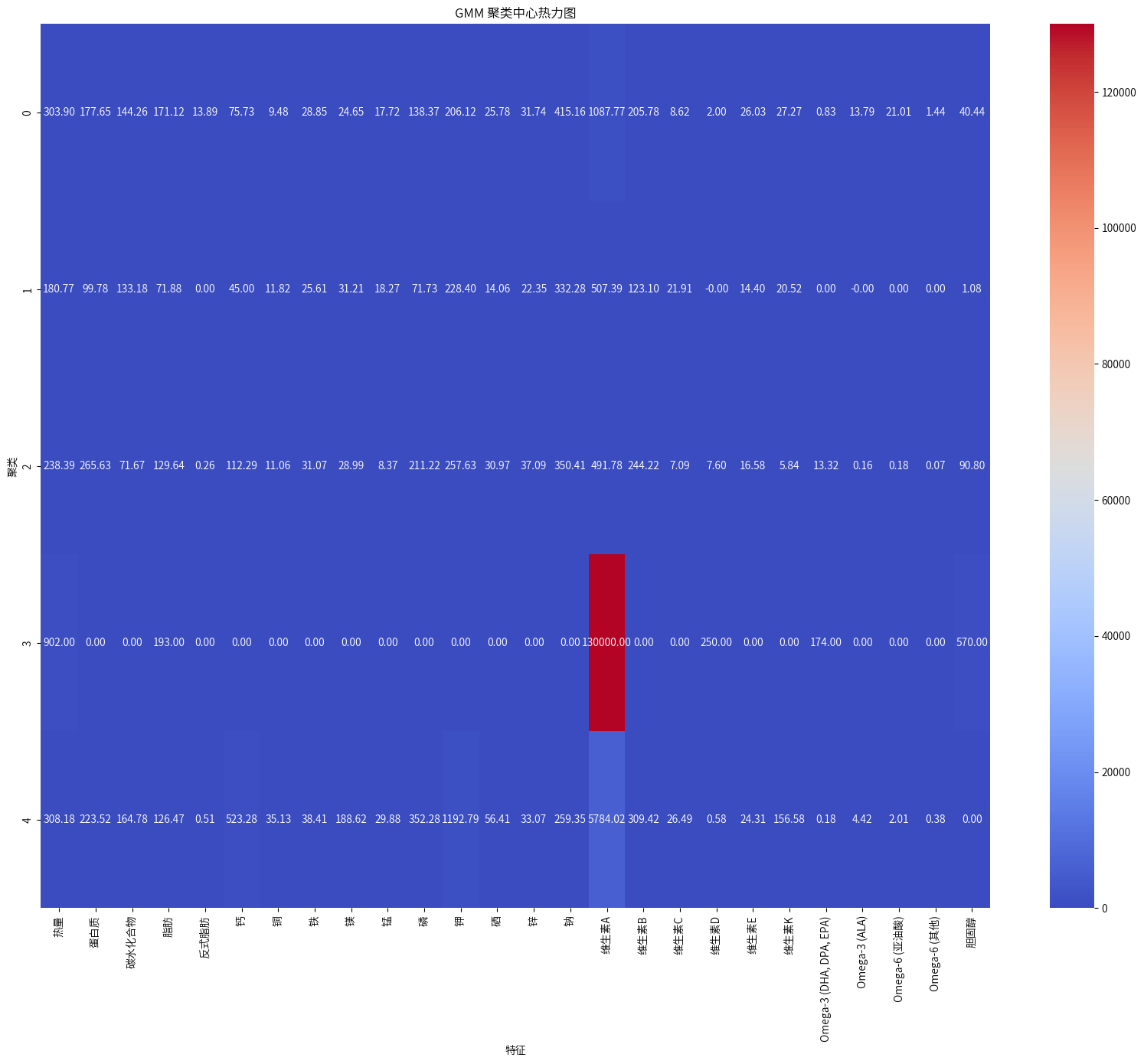
基于多维统计分析与GMM聚类的食品营养特征研究
1.项目背景 在当今社会,随着人们对健康和营养的日益关注,深入了解食品的营养成分及其对人体的影响变得越来越重要,本研究采用了多维度的分析方法,包括营养成分比较分析、统计检验、营养密度分析和高斯混合模型(GMM&am…...

SkyWalking 告警功能
SkyWalking 告警功能是在 6.x 版本新增的,其核心由一组规则驱动,这些规则定义在config/alarm-settings.yml文件中。 告警规则 告警规则:它们定义了应该如何触发度量警报,应该考虑什么条件。Webhook(网络钩子):定义当警告触发时,哪些服务终端需要被告知。常用告警规则 …...
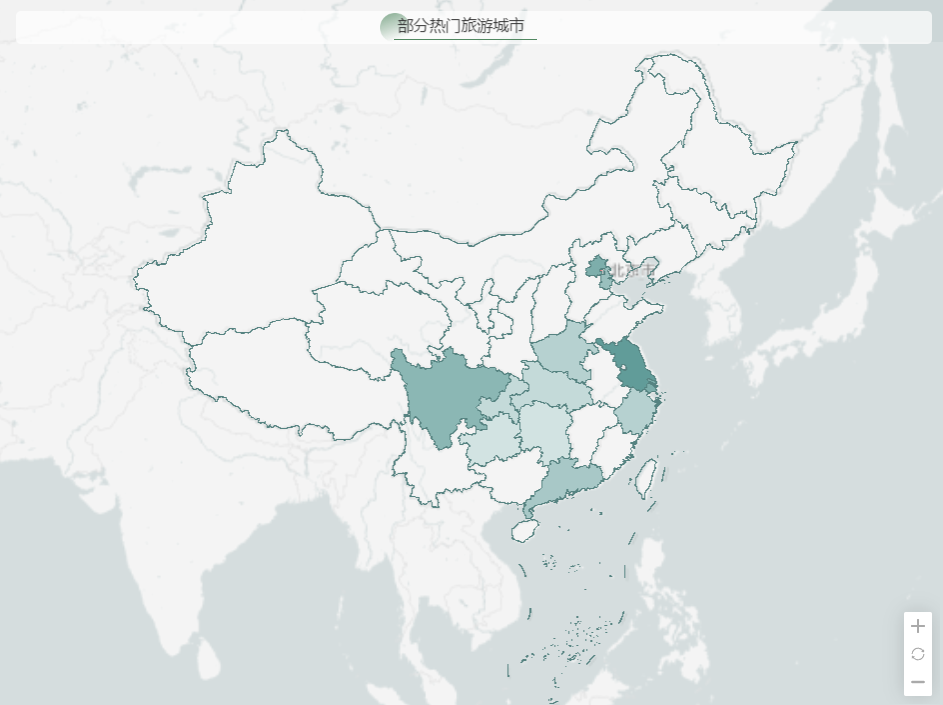
国内旅游:现状与未来趋势分析
在当今社会快速发展的背景下,国内旅游更是呈现出蓬勃的发展态势。中国,这片拥有悠久历史、灿烂文化和壮丽山河的广袤土地,为国内旅游的兴起与发展提供了得天独厚的条件。 本报告将借助 DataEase 强大的数据可视化分析能力,深入剖…...
西电25考研 VS 24考研专业课大纲变动汇总
01专业课变动 西安电子科技大学专业课学长看到953网络安全基础综合变为 893网络安全基础综合,这是因为工科要求都必须是8开头的专业课,里面参考课本还是没变的,无非就是变了一个名字 对于其他变动专业课也是同理的 02专业课考纲内容变化 对于…...

【Linux】进程管理:状态与优先级调度的深度分析
✨ 山海自有归期,风雨自有相逢 🌏 📃个人主页:island1314 🔥个人专栏:Linux—登神长阶 ⛺️ 欢迎关注:👍点赞 …...

同轴电缆笔记
同轴电缆笔记 射频同轴电缆的阻抗标准为什么是50Ω或75Ω呢? 在PCB设计中,在合理的范围内,传输线阻抗的具体数值并不重要。只要控制好整条传输线的阻抗,不要出现阻抗不连续的情况就好了。设计中的其他因素往往决定了我们用什么样…...

【Verilog学习日常】—牛客网刷题—Verilog企业真题—VL74
异步复位同步释放 描述 题目描述: 请使用异步复位同步释放来将输入数据a存储到寄存器中,并画图说明异步复位同步释放的机制原理 信号示意图: clk为时钟 rst_n为低电平复位 d信号输入 dout信号输出 波形示意图: 输入描…...

在Linux系统安装Nginx
注意:Nginx端口号是80(云服务器要放行) 我的是基于yum源安装 安装yum源(下面这4步就好了) YUM源 1、将源文件备份 cd /etc/yum.repos.d/ && mkdir backup && mv *repo backup/ 2、下载阿里源文件 curl -o /etc/yum.repos.d/CentOS-Base.repo ht…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...








