12.梯度下降法的具体解析——举足轻重的模型优化算法
引言
梯度下降法(Gradient Descent)是一种广泛应用于机器学习领域的基本优化算法,它通过迭代地调整模型参数,最小化损失函数以求得到模型最优解。
通过阅读本篇博客,你可以:
1.知晓梯度下降法的具体流程
2.掌握不同梯度下降法的区别
一、梯度下降法的流程
梯度下降法的流程通常分为以下四个步骤。

1.初始化模型参数
初始化模型参数其实就是random随机一个初始的 (一组
)。这样我们就可以得到上图中的 Starting Point(开始点)。
2.计算当下参数的梯度
计算模型参数的梯度,其实就是对于当前损失函数所在位置进行求偏导,公式:
公式推导 是损失函数,
是样本中某个特征维度
对应的权值系数,也可以写成
。对于多元线性回归来说,损失函数
(推导过程在9.深入线性回归推导出MSE——不容小觑的线性回归算法-CSDN博客中),因为我们的MSE中
、
是已知的,
是未知的,而
不是一个变量而是许多向量组成的矩阵,所以我们只能对含有一堆变量的函数MSE中的一个变量求导,即偏导,下面就是对
求偏导。
由于链式求导法则,我们可以推出:
在多元线性回归中, 就是
,也就是
,我们通常把它写成
,所以继续推导公式:
由于我们是对 求偏导,那么和
无关的可以忽略不计,所以公式变为:
所以,我们可以得到结论: 对应的梯度(gradient)与预测值
和真实值
有关,同时还与每个特征维度
有关。如果我们分别对每个维度求偏导,即可得到所有维度对应的梯度值。
3.根据梯度和学习率更新参数
通过11.梯度下降法的思想——举足轻重的模型优化算法-CSDN博客的学习,我们已经知道了梯度下降法的公式:
在获得了梯度之后,我们可以将公式表示为:
通过这个公式我们就可以去更新参数逼近最优解。
4.判断是否收敛
在如何判断收敛问题上,我相信大多数的人都会认为直接判断梯度(gradient)是否为0。其实这样的方法是错误的,由于非凸损失函数的存在, 的情况可能是极大值!所以我们使用了另外一种方法,设置合理的阈值(Threshold)来界定函数是否收敛。即判断不等式:
如果前一次的损失函数 减去这次迭代后的损失函数
小于我们设定的阈值
,那我们认为函数收敛,当前的参数就是我们寻求的最优解。反之,我们重复第二步与第三步,一直达到最优解为止。其实我们是在判断
的下降收益是否更合理,随着迭代次数的增多,
减小的幅度不再变化就可以认为停止在最低点。
二、梯度下降法的分类
我们根据梯度下降法流程中求取梯度的步骤样本数量的不同,将梯度下降法分为三个基本的类别。它们每次学习(更新模型参数)使用的样本个数,每次更新使用不同的样本会导致每次学习的准确性和学习时间不同。

1.全量梯度下降(Batch Gradient Descent)
全量梯度下降(Batch Gradient Descent)通过使用整个数据集在每次迭代中计算损失函数的梯度,以此更新模型参数(也称批量梯度下降)。由于我们使用整个数据集的样本,所以全量梯度下降的公式为:
在全量梯度下降中,对于 的更新,所有的样本都有贡献,也就是参与调整
。所以从理论上来说一次更新的幅度是比较大的。
全量梯度下降法的优点在于收敛稳定,每次更新都朝着全局最优的方向移动。并且能够净化噪声,由于使用整个数据集计算梯度,随机噪声对更新的影响较小,使得损失函数的路径相对平滑。
缺点也是相当明显,当数据集非常大时,全量梯度下降法每个迭代计算数据集的梯度是非常耗时且占用内存的。所以不适合处理实时数据,比如在线学习和实时更新数据场景。

上图表示的梯度下降法中两个维度参数的关系,我们可以将圆圈看成一个碗的俯视图,碗底就是我们要找的最优解。我们不难发现,全量梯度下降法每次迭代都直接向碗底行进,目标明确。
2.随机梯度下降(Stochastic Gradient Descent)
随机梯度下降(Stochastic Gradient Descent)通过使用数据集中的一个随机样本在每次迭代中计算损失函数的梯度,以此更新模型参数。由于使用随机的一个样本,所以随机梯度下降的公式就是:
随机梯度下降的优点在于计算速度快,由于每次迭代只对一个样本计算梯度,因此更新速度快,适合大规模数据集。它还拥有更强的泛化能力,由于引入了随机性,SGD能更好地跳出局部最优,避免过拟合(过拟合相关内容会在专栏后续文章中更新)。并且能够处理实时数据,可以在线学习,所以适用于动态更新的场景。
同样地,由于每次更新只基于一个样本,SGD的收敛并不稳定,梯度波动较大,会导致损失函数的收敛路径不平稳。并且由于随机性的存在,SGD通常需要更多的迭代次数才能收敛到最优解,即收敛速度变慢。

从上图我们可以看出,相比较全量梯度下降,SGD需要迭代更多的次数才能找到最优解。
3.小批量梯度下降(Mini-batch Gradient Descent)
小批量梯度下降(Mini-batch Gradient Descent)通过使用数据集的一部分样本在每次迭代中计算损失函数的梯度,以此更新模型参数。由于使用了数据集的部分样本,所以小批量梯度下降的公式为:
小批量梯度下降综合了全量梯度下降与随机梯度下降,在更新速度与更新次数中取得一个平衡。其每次更新从数据集中随机选择 个样本进行学习。相对于随机梯度下降法,小批量梯度下降法降低了收敛的波动性(降低了参数更新的方差),使得更新更加稳定。相对于全量梯度下降法,其提高了每次学习的速度。
小批量梯度下降的优点在于平衡了计算效率和收敛稳定性。并且不用担心内存瓶颈而使用向量化计算,还能利用GPU的并行计算能力提高计算速度。在每个小批量中,我们可以设置不同的学习率,提高模型的训练表现。
小批量梯度下降的缺点则在于样本的大小会影响训练效果,所以我们要人为地选择合适的样本大小。
从下图中我们就能看到随机梯度下降与小批量梯度下降的区别。

总结
本篇博客讲解了梯度下降法的流程和大致的分类。希望可以对大家起到作用,谢谢。
关注我,内容持续更新(后续内容在作者专栏《从零基础到AI算法工程师》)!!!

相关文章:

12.梯度下降法的具体解析——举足轻重的模型优化算法
引言 梯度下降法(Gradient Descent)是一种广泛应用于机器学习领域的基本优化算法,它通过迭代地调整模型参数,最小化损失函数以求得到模型最优解。 通过阅读本篇博客,你可以: 1.知晓梯度下降法的具体流程 2.掌握不同梯度下降法…...

GPT对话知识库——C、C++,还有Java,他们之间有什么区别
目录 1,问: 1,答: 1. 语言特性与设计理念 C 语言: C 语言: Java 语言: 2. 内存管理 3. 运行效率 C 和 C: Java: 4. 程序的执行方式 C 和 C: Jav…...

华为GaussDB数据库之Yukon安装与使用
一、Yukon简介 Yukon(禹贡),基于openGauss、PostgreSQL、GaussDB数据库扩展地理空间数据的存储和管理能力,提供专业的GIS(Geographic Information System)功能,赋能传统关系型数据库。 Yukon 支…...

Linux命令:用于显示 Linux 发行版信息的命令行工具lsb_release详解
目录 一、概述 二、用法 1、基本用法 2、选项 3、获取帮助 三、示例 1. 显示所有信息 2. 只显示发行版名称 3. 只显示发行版版本号 4. 只显示发行版代号 5. 只显示发行版描述 6. 只显示值,不显示标签 四、使用场景 1、自动化脚本 2、诊断问题 3、环…...

sbb-classes 元素
sbb-classes 元素 在 JAIN SLEE(服务级别事件扩展)中,sbb-classes 元素用于定义服务边界组件(SBB)的类结构及其相关配置。这是每个 SBB 的必备部分,包含多个子元素,负责描述 SBB 的抽象类、接口…...
(作业)第三期书生·浦语大模型实战营(十一卷王场)--书生入门岛通关第3关Git 基础知识
任务编号 任务名称 任务描述 1 破冰活动 提交一份自我介绍。 2 实践项目 创建并提交一个项目。 破冰活动 提交一份自我介绍。 每位参与者提交一份自我介绍。 提交地址:https://github.com/InternLM/Tutorial 的 camp3 分支~ 安装并设置git 克隆仓库并…...

12.数据结构和算法-栈和队列的定义和特点
栈和队列的定义和特点 栈的应用 队列的常见应用 栈的定义和特点 栈的相关概念 栈的示意图 栈与一般线性表有什么不同 队列的定义和特点 队列的相关概念...

15分钟学 Python 第34天 :小项目-个人博客网站
Day 34: 小项目-个人博客网站 1. 引言 随着互联网的普及,个人博客已成为分享知识、体验和见解的一个重要平台。在这一节中,我们将使用Python的Flask框架构建一个简单的个人博客网站。我们将通过实际的项目来学习如何搭建Web应用、处理用户输入以及管理…...

从零开始实现RPC框架---------项目介绍及环境准备
一,介绍 RPC(Remote Procedure Call)远程过程调⽤,是⼀种通过⽹络从远程计算机上请求服务,⽽不需要 了解底层⽹络通信细节。RPC可以使⽤多种⽹络协议进⾏通信, 如HTTP、TCP、UDP等, 并且在 TCP/…...
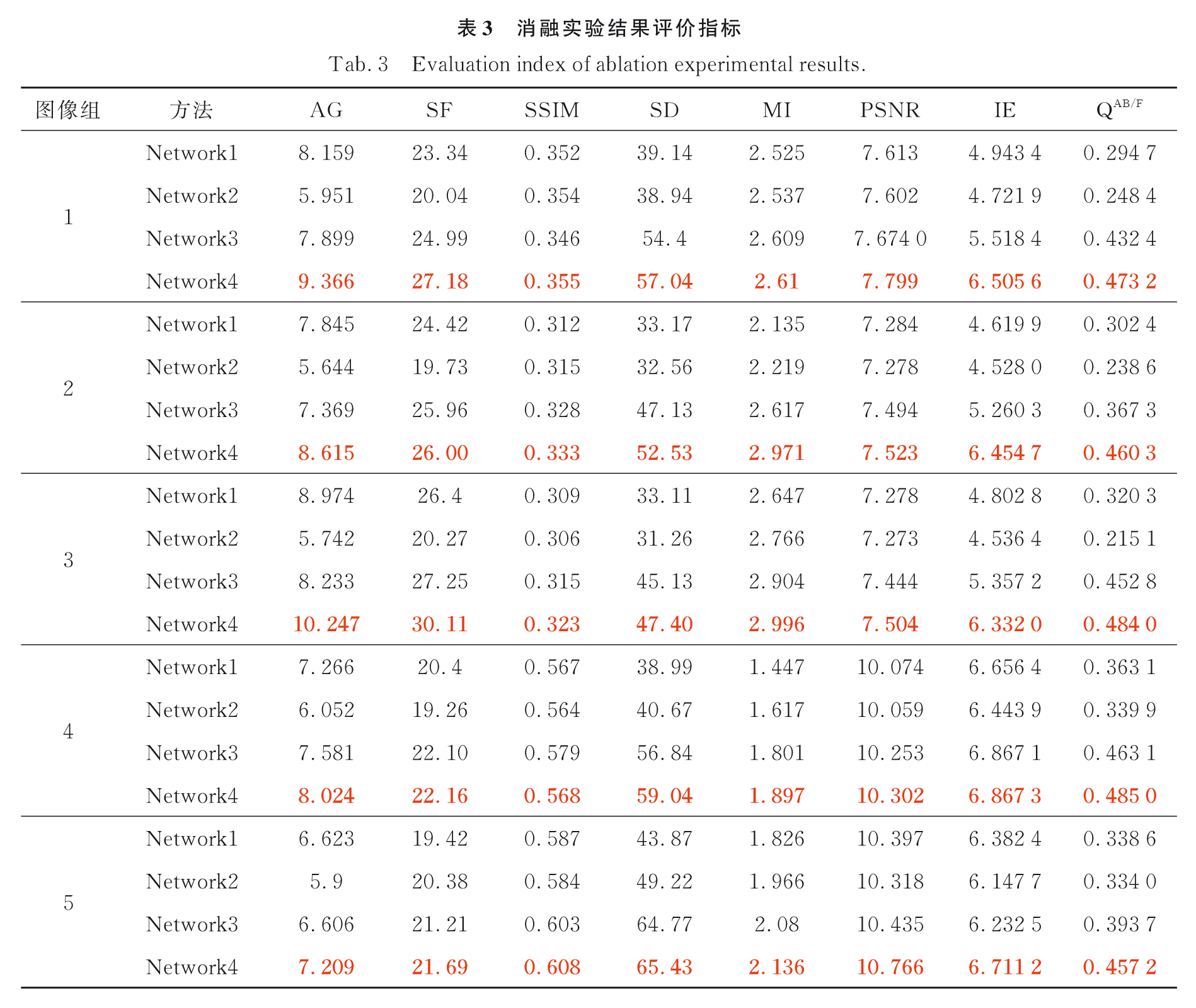
论文阅读:PET/CT Cross-modal medical image fusion of lung tumors based on DCIF-GAN
摘要 背景: 基于GAN的融合方法存在训练不稳定,提取图像的局部和全局上下文语义信息能力不足,交互融合程度不够等问题 贡献: 提出双耦合交互式融合GAN(Dual-Coupled Interactive Fusion GAN,DCIF-GAN&…...

java基础 day1
学习视频链接 人机交互的小故事 微软和乔布斯借鉴了施乐实现了如今的图形化界面 图形化界面对于用户来说,操作更加容易上手,但是也存在一些问题。使用图形化界面需要加载许多图片,所以消耗内存;此外运行的速度没有命令行快 Wi…...

cpp,git,unity学习
c#中的? 1. 空值类型(Nullable Types) ? 可以用于值类型(例如 int、bool 等),使它们可以接受 null。通常,值类型不能为 null,但是通过 ? 可以表示它们是可空的。 int? number null; // …...

HTML增加文本复制模块(使用户快速复制内容到剪贴板)
增加复制模块主要是为了方便用户快速复制内容到剪贴板,通常在需要提供文本信息可以便捷复制的网页设计或应用程序中常见。以下是为文本内容添加复制按钮的一个简单实现步骤: HTML结构: 在文本旁边添加一个复制按钮,例如 <butto…...

Spring Cloud面试题收集
Spring Cloud Spring cloud 是一系列框架的有序集合。它利用 spring boot 的开发便利性巧妙地简化了分布式系统基础设施的开发,如服务发现注册、配置中心、消息总线、负载均衡、断路器、数据监控等,都可以用 spring boot 的开发风格做到一键启动和部署。…...
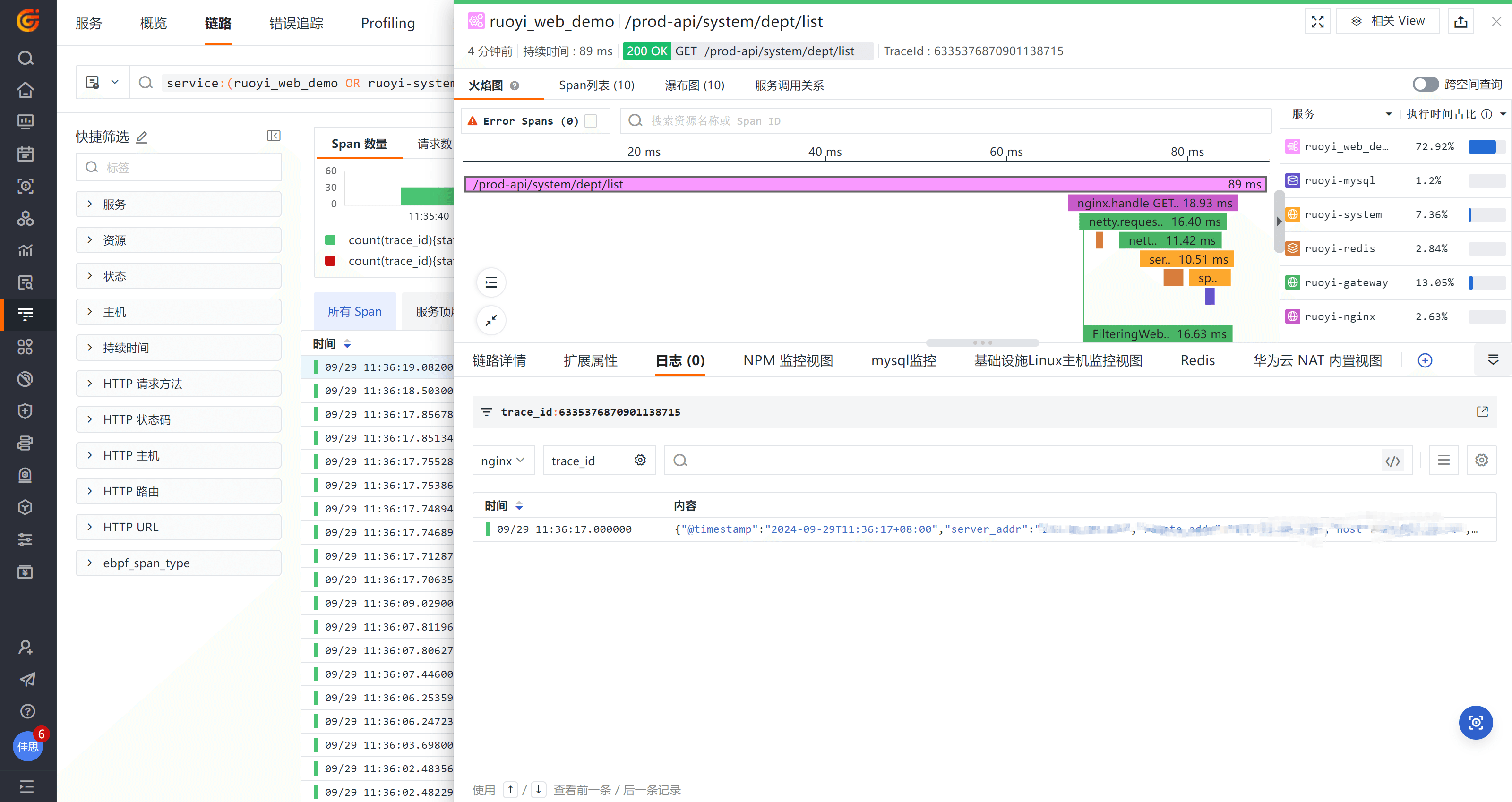
观测云对接 SkyWalking 最佳实践
简介 SkyWalking 是一个开源的 APM(应用性能监控)和可观测性分析平台,专为微服务、云原生架构和基于容器的架构设计。它提供了分布式追踪、服务网格遥测分析、度量聚合和可视化一体化的解决方案。如果您的应用中正在使用SkyWalking …...

AI少女/HS2甜心选择2 仿天刀人物卡全合集打包
内含AI少女/甜心选择2 仿天刀角色卡全合集打包共21张 下载地址:https://www.51888w.com/408.html 部分演示图:...

MISC - 第11天(练习)
前言 各位师傅大家好,我是qmx_07,今天继续讲解MISC的相关知识 john-in-the-middle 导出http数据文件里面logo.png 是旗帜图案,放到stegsolve查看 通过转换颜色,发现flag信息 flag{J0hn_th3_Sn1ff3r} [UTCTF2020]docx 附件信息…...

[3.4]【机器人运动学MATLAB实战分析】PUMA560机器人逆运动学MATLAB计算
PUMA560是六自由度关节型机器人,其6个关节都是转动副,属于6R型操作臂。各连杆坐标系如图1,连杆参数如表1所示。 图1 PUMA560机器人的各连杆坐标系 表1 PUMA560机器人的连杆参数 用代数法对其进行运动学反解。具体步骤如下: 1、求θ1 PMUMA56...

centos常用知识和命令
linux目录及结构 /etc #存配置文件 /var #存日志文件 /home #用户家目录 /root #root用户家目录 /bin #命令文件目录 /sbin #超级管理员命令目录 /dev #设备文件目录 /boot #系统启动核心目录 /lib #库文件目录 /mnt #挂载目录 /tmp #临时文件目录 /usr #用户程序存…...

基于yolov8调用本地摄像头并将读取的信息传入jsonl中
最近在做水面垃圾识别的智能船 用到了yolov8进行目标检测 修改并添加了SEAttention注意力机制 详情见其他大神 【保姆级教程|YOLOv8添加注意力机制】【1】添加SEAttention注意力机制步骤详解、训练及推理使用_yolov8添加se-CSDN博客 并且修改传统的iou方法改为添加了wise-io…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
