常见排序算法汇总
排序算法汇总
这篇文章说明下排序算法,直接开始。
1.冒泡排序
最简单直观的排序算法了,新手入门的第一个排序算法,也非常直观,最大的数字像泡泡一样一个个的“冒”到数组的最后面。
算法思想:反复遍历要排序的序列,每次比较相邻的两个元素,如果顺序不正确就交换它们。这样每次遍历都会将最大的元素放到末尾。
排序的时间复杂度O(n²),如果设置标志为(如果发生数据交换flag=1,默认为0)复杂度为O(n),,因为是原地排序,基本不用。
void bubble_sort(vector<int> &nums) {int n = nums.size();for (int i = 0; i < n-1; i++) {for (int j = 0; j < n-i-1; j++) {if (nums[j] > nums[j+1]) {swap(nums[j], nums[j+1]);}}}
}
2.选择排序
算法思想:每次从未排序的部分选择最小的元素,放到已排序部分的末尾,重复这个过程。时间复杂度:O(n²),无论怎样都是O(n²),空间复杂度O(1),基本不用。
void selectionSort(std::vector<int> &arr) {int n = arr.size();for (int i = 0; i < n - 1; ++i) {int minIndex = i; // 假设当前元素为最小值的索引for (int j = i + 1; j < n; ++j) { // 在未排序部分查找最小值if (arr[j] < arr[minIndex]) {minIndex = j; // 更新最小值索引}}// 将找到的最小值与当前元素交换if (minIndex != i) {std::swap(arr[i], arr[minIndex]);}}
}
3.插入排序
算法思想:将数组分为已排序和未排序部分,从未排序部分取元素,在已排序部分找到合适的位置插入。时间复杂度O(n²),空间复杂度O(1)。
void insertionSort(std::vector<int>& arr) {int n = arr.size(); // 获取数组的大小for (int i = 1; i < n; i++) { // 从第二个元素开始int key = arr[i]; // 当前待插入的元素int j = i - 1;// 在已排序部分中找到合适的位置插入 keywhile (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j]; // 向后移动元素j--; // 移动到前一个元素}arr[j + 1] = key; // 插入 key}
}
4.快速排序
算法思想:选择一个基准元素,将数组划分为比基准小的部分和比基准大的部分,递归地对这两个部分排序。时间复杂度O(n log n),空间复杂度O(log n) 。
void fastSort(vector<int> &nums, int low, int high) {if (low >= high)return;int pivot = nums[high], i = low;for (int j = low; j < high; j++) {if (nums[j] < pivot) {if (i != j)swap(nums[i], nums[j]);i++;}}swap(nums[i], nums[high]);fastSort(nums, low, i - 1);fastSort(nums, i + 1, high);
}
5.归并排序
算法思想:采用分治法,将数组分成两个子数组分别排序,再将它们合并成一个有序数组。时间复杂度O(n log n),空间复杂度O(n) 。
//递归版本
void mergeSort(vector<int> &nums, int left, int right) {if (left >= right)return;int mid = left + (right - left)/2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);vector<int> tmp(right - left + 1);int count = 0;int i = left, j = mid + 1;while (i <= mid && j <= right) {if (nums[i] < nums[j]) {tmp[count++] = nums[i++];} else {tmp[count++] = nums[j++];}}while (i <= mid) {tmp[count++] = nums[i++];}while (j <= right) {tmp[count++] = nums[j++];}for (int p = 0; p < tmp.size(); p++) {nums[left + p] = tmp[p];}
}
//迭代版本
void mergeSortIterative(std::vector<int> &nums) {int n = nums.size();for (int currentsize = 1; currentsize < n - 1; currentsize *= 2)for (int left = 0; left < n - 1; left += 2 * currentsize) {int mid = min(left + currentsize - 1, n - 1);int right = min(left + 2 * currentsize - 1, n - 1);int n1 = mid - left + 1;int n2 = right - mid;vector<int> leftArr(n1), rightArr(n2);for (int i = 0; i < n1; i++)leftArr[i] = nums[left + i];for (int i = 0; i < n2; i++)rightArr[i] = nums[mid + i + 1];int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (leftArr[i] < rightArr[j]) {nums[k] = leftArr[i++];} else {nums[k] = rightArr[j++];}k++;}while (i < n1) {nums[k++] = leftArr[i++];}while (j < n2) {nums[k++] = rightArr[j++];}}
}
6.堆排序
算法思想:使用二叉堆这种数据结构,先构建最大堆(或最小堆),然后依次将堆顶元素移除,重新调整堆。时间复杂度O(n log n),空间复杂度O(1)(不用递归的话)
void heapify(vector<int> &nums, int n, int i) {if(i>n)return;int largest = i;int left = 2 * i + 1, right = 2 * i + 2;if (left < n && nums[left] > nums[largest])largest = left;if (right < n && nums[right] > nums[largest])largest = right;if (largest != i) {swap(nums[i], nums[largest]);heapify(nums, n, largest);}}void heapSort(vector<int> &nums) {int n = nums.size();for(int i=n/2-1;i>=0;i--) {heapify(nums,n,i);}for(int i=n-1;i>0;i--) {swap(nums[0],nums[i]);heapify(nums,i,0);}
}
排序算法的总结表格:
| 排序算法 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 |
| 插入排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | O(log n) | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 |
7.文末解释一下算法时间复杂中的log n,有些人不理解
快速排序的平均时间复杂度为 O(n log n),是因为它在理想情况下可以将问题规模递归减半,而每次递归的划分过程需要 O(n) 的操作。通过递归树的结构,我们可以直观理解为什么时间复杂度为 O(n log n)。
1. 每一层的操作需要 O(n) 的时间
在快速排序的每一层递归中,主要的开销来自于划分(partition)操作。这个操作的过程是选取一个基准元素(pivot),然后从两边扫描数组,交换元素,使得基准元素的左边都比它小,右边都比它大。
无论基准元素选得如何,每次划分需要遍历整个数组。因此,在每一层递归中,划分操作的时间复杂度是 O(n),其中 n 是当前数组的长度。
2. 递归的层数为 log n
在理想情况下,快速排序的每次递归都能将数组大致划分为相等的两部分,即每次递归之后,数组的规模缩小为原来的 1/2。这个过程相当于将问题规模递归地减半,直到数组大小缩减到 1。
因此,总共需要递归 log n 层(递归树的高度),这里的 log n 表示递归树的层数,也就是快速排序的递归深度。
3. 总时间复杂度为 O(n log n)
- 每层的时间复杂度:在递归树的每一层,需要
O(n)的时间来对数组进行划分。 - 递归树的层数:递归树的高度为
log n,表示总共要递归log n层。
因此,整个快速排序的总时间复杂度就是:
总时间=每层所需的时间×递归的层数=O(n)×O(logn)=O(nlogn)
递归树示意:
可以将快速排序的递归过程看作是一个递归树,每一层是对整个数组的遍历,每一层都需要 O(n) 的时间来进行划分。递归树的层数是 log n,总共 log n 层。
举例说明递归树结构:
O(n)----------------| |O(n/2) O(n/2)------- -------| | | |O(n/4) O(n/4) O(n/4) O(n/4)----------------------------... (共 log n 层)
4. 平均时间复杂度为 O(n log n) 的解释
在理想情况下,每次划分都能把数组平分成两半,快速排序的递归树的高度为 log n。每一层递归处理的元素总数为 n(即整个数组的长度),由于有 log n 层,所以整个快速排序的总时间复杂度为 O(n log n)。
5. 总结:
- 每一层快速排序的递归操作需要
O(n)的时间来进行划分。 - 总共有
log n层递归,即递归树的高度为log n。 - 因此,快速排序的平均时间复杂度是
O(n log n)。
不过需要注意,在最坏情况下(当每次划分都极不平衡,如数组是完全有序的),递归树的高度会退化为 n,此时时间复杂度为 O(n^2)。通过随机化选择基准元素,可以有效避免这种最坏情况的发生,从而保证平均时间复杂度为 O(n log n)。
相关文章:

常见排序算法汇总
排序算法汇总 这篇文章说明下排序算法,直接开始。 1.冒泡排序 最简单直观的排序算法了,新手入门的第一个排序算法,也非常直观,最大的数字像泡泡一样一个个的“冒”到数组的最后面。 算法思想:反复遍历要排序的序列…...

Golang | Leetcode Golang题解之第459题重复的子字符串
题目: 题解: func repeatedSubstringPattern(s string) bool {return kmp(s s, s) }func kmp(query, pattern string) bool {n, m : len(query), len(pattern)fail : make([]int, m)for i : 0; i < m; i {fail[i] -1}for i : 1; i < m; i {j : …...

0.计网和操作系统
0.计网和操作系统 熟悉计算机网络和操作系统知识,包括 TCP/IP、UDP、HTTP、DNS 协议等。 常见的页面置换算法: 先进先出(FIFO)算法:将最早进入内存的页面替换出去。最近最少使用(LRU)算法&am…...

探索Prompt Engineering:开启大型语言模型潜力的钥匙
前言 什么是Prompt?Prompt Engineering? Prompt可以理解为向语言模型提出的问题或者指令,它是激发模型产生特定类型响应的“触发器”。 Prompt Engineering,即提示工程,是近年来随着大型语言模型(LLM,Larg…...
)
滚雪球学Oracle[3.3讲]:数据定义语言(DDL)
全文目录: 前言一、约束的高级使用1.1 主键(Primary Key)案例演示:定义主键 1.2 唯一性约束(Unique)案例演示:定义唯一性约束 1.3 外键(Foreign Key)案例演示:…...

ssrf学习(ctfhub靶场)
ssrf练习 目录 ssrf类型 漏洞形成原理(来自网络) 靶场题目 第一题(url探测网站下文件) 第二关(使用伪协议) 关于http和file协议的理解 file协议 http协议 第三关(端口扫描)…...

ElasticSearch之网络配置
对官方文档Networking的阅读笔记。 ES集群中的节点,支持处理两类通信平面 集群内节点之间的通信,官方文档称之为transport layer。集群外的通信,处理客户端下发的请求,比如数据的CRUD,检索等,官方文档称之…...

【C语言进阶】系统测试与调试
1. 引言 在开始本教程的深度学习之前,我们需要了解整个教程的目标及其结构,以及为何进阶学习是提升C语言技能的关键。 目标和结构: 教程目标:本教程旨在通过系统化的学习,从单元测试、系统集成测试到调试技巧…...

多个单链表的合成
建立两个非递减有序单链表,然后合并成一个非递增有序的单链表。 注意:建立非递减有序的单链表,需要采用创建单链表的算法 输入格式: 1 9 5 7 3 0 2 8 4 6 0 输出格式: 9 8 7 6 5 4 3 2 1 输入样例: 在这里给出一组输入。例如…...

『建议收藏』ChatGPT Canvas功能进阶使用指南!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,专注于分享AI全维度知识,包括但不限于AI科普,AI工…...

Ollama 运行视觉语言模型LLaVA
Ollama的LLaVA(大型语言和视觉助手)模型集已更新至 1.6 版,支持: 更高的图像分辨率:支持高达 4 倍的像素,使模型能够掌握更多细节。改进的文本识别和推理能力:在附加文档、图表和图表数据集上进…...

gdb 调试 linux 应用程序的技巧介绍
使用 gdb 来调试 Linux 应用程序时,可以显著提高开发和调试的效率。gdb(GNU 调试器)是一款功能强大的调试工具,适用于调试各类 C、C 程序。它允许我们在运行程序时检查其状态,设置断点,跟踪变量值的变化&am…...

Java项目实战II基于Java+Spring Boot+MySQL的房产销售系统(源码+数据库+文档)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者 一、前言 随着房地产市场的蓬勃发展,房产销售业务日益复杂,传统的手工管理方式已难以满…...

aws(学习笔记第一课) AWS CLI,创建ec2 server以及drawio进行aws画图
aws(学习笔记第一课) 使用AWS CLI 学习内容: 使用AWS CLI配置密钥对创建ec2 server使用drawio(vscode插件)进行AWS的画图 1. 使用AWS CLI 注册AWS账号 AWS是通用的云计算平台,可以提供ec2,vpc,SNS以及clo…...

【Python】Eventlet 异步网络库简介
Eventlet 是一个 Python 的异步网络库,它使用协程(green threads)来简化并发编程。通过非阻塞的 I/O 操作,Eventlet 使得你可以轻松编写高性能的网络应用程序,而无需处理复杂的回调逻辑或编写多线程代码。它广泛应用于…...
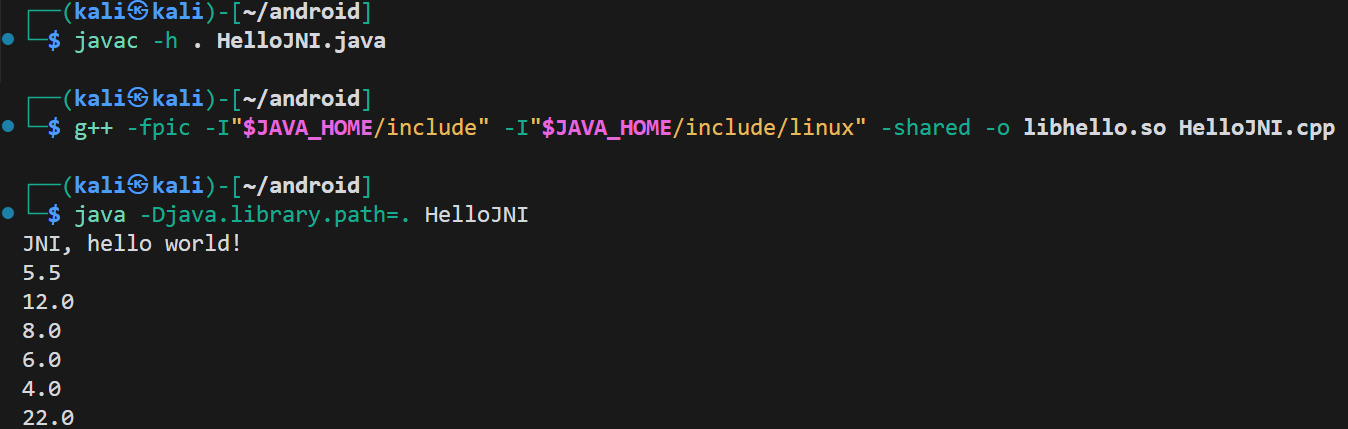
【JNI】数组的基本使用
在上一期讲了基本类型的基本使用,这期来说一说数组的基本使用 HelloJNI.java:实现myArray函数,把一个整型数组转换为双精度型数组 public class HelloJNI { static {System.loadLibrary("hello"); }private native String HelloW…...

React跨平台
React的跨平台应用开发详解如下: 一、跨平台能力 React本身是一个用于构建用户界面的JavaScript库,但它通过React Native等框架实现了跨平台应用开发的能力。React Native允许开发者使用JavaScript和React来编写原生应用,这些应用可以在iOS和…...

如何在 SQL 中更新表中的记录?
当你需要修改数据库中已存在的数据时,UPDATE 语句是你的首选工具。 这允许你更改表中一条或多条记录的特定字段值。 下面我将详细介绍如何使用 UPDATE 语句,并提供一些开发建议和注意事项。 基础用法 假设我们有一个名为 employees 的表,…...

宠物饮水机的水箱低液位提醒如何实现?
ICMAN液位检测芯片轻松实现宠物饮水机的水箱低液位提醒功能! 工作原理 : 基于双通道电容式单点液位检测原理 方案特点: 液位检测精度高达1mm,超强抗干扰,动态CS 10V 为家用电器水位提醒的应用提供了一种简单而又有…...

EXCEL_光标百分比
Public Sub InitCells()Dim iSheet As LongFor iSheet Sheets.Count To 1 Step -1Sheets(iSheet).ActivateActiveWindow.Zoom 85ActiveWindow.ScrollRow 1ActiveWindow.ScrollColumn 1Sheets(iSheet).Range("A1").ActivateNext iSheetEnd Sub对日项目中的文档满天…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
