个人文章合集 - 前端相关
前端：简述表单提交前如何进行数据验证
前端：项目一个html中如何引入另一个html？
前端：一张图快速记忆CSS所有属性
前端：三个CSS预处理器(框架)-Sass、LESS 和 Stylus的比较
前端：基于Java角度理解nodejs/npm/webpack
Jquery：验证InputFile选中的文件类型
Vue：简述对Vue的简单认识
Vue：Vue2.0常用的开发环境
Vue：Windows环境下搭建Vue的开发环境
Vue：优秀的Vue UI组件库总结
Vue：简述Vue开发中的NaN类型
Vue：父子组件之间的接口互调
Vue：SessionStorage存储-读取字符串和对象
Vue：通过Vue.prototype定义原型属性实现全局变量
Vue：Vue+ElementUI+Axios实现全局接口请求的加载动画
Vue：Vue项目打包后，使浏览器WebPack中不能查看源码
相关文章：
个人文章合集 - 前端相关
前端：简述表单提交前如何进行数据验证 前端：项目一个html中如何引入另一个html？ 前端：一张图快速记忆CSS所有属性 前端：三个CSS预处理器(框架)-Sass、LESS 和 Stylus的比较 前端：基于Java角度理解nodejs/np…...
R语言的下载、安装及环境配置（RstudioVSCode）
0x01 R语言篇 一、软件介绍 R for Windows是一个免费的用于统计计算和统计制图的优秀工具，是R语言开发工具。它拥有数据存储和处理系统、数组运算工具（其向量、矩阵运算方面功能尤其强大）、完整连贯的统计分析工具、优秀的统计制图等功能。…...
解决使用重载后的CustomWidget无法正常显示但原生的QWidget却能正常显示的问题
这种情况大部分都是因为没有重写paintEvent: #include <QPainter> #include <QStyleOption>void CustomWidget::paintEvent(QPaintEvent *) { QStyleOption opt; opt.initFrom(this); QPainter p(this); style()->drawPrimitive(QStyle::PE_Widget, &opt,…...
微服务Sleuth解析部署使用全流程
目录 1、Sleuth链路追踪 1、添加依赖 2、修改日志配置文件 3、测试 2、zipkin可视化界面 1、docker安装 2、添加依赖 3、修改配置文件 4、查看页面 5、ribbon配置 1、Sleuth链路追踪 sleuth是链路追踪框架，用于在微服务架构下开发，各个微服务之…...
最具有世界影响力的人颜廷利：全球著名哲学家思想家起名大师
颜廷利教授，这位源自济南唐王镇的杰出人物，不仅是中国当代最杰出的国学大师之一，更是将传统文化与现代科技巧妙结合的先锋。他积极推崇以人工智能技术为辅助的国学研究方法，为这一古老领域注入了新的活力和时代表达。 除了在学术…...
Ubuntu22.04 Docker 国内安装最靠谱教程
目前docker在国内安装常存在众所周知的网络问题，如果安装过程如果从官网地址安装以及安装之后从官网要拉取镜像都存在问题。这篇文章主要针对这两个问题总结最靠谱的docker安装教程。 1. docker安装 1.1 系统环境概述 Ubuntu 22.04linux内核版本 6.8（…...
ceph pg rebalance
背景 1 个 osd full 超过 85% 使用率最近有大量的数据写入及数据删除操作 $ ceph osd df tree | grep osd.158 ID CLASS WEIGHT REWEIGHT SIZE RAW USE DATA OMAP META AVAIL %USE VAR PGS STATUS TYPE NAME …...
大模型/Sora/世界模型之间是什么关系，对自动驾驶的意义是什么？
什么是大模型 人工智能大模型（Artificial Intelligence Large Model，简称AI大模型）是指具有庞大的参数规模和复杂程度的机器学习模型。通常指的是参数量非常大、数据量非常大的深度学习模型。 大模型通常由数百万到数十亿的参数组成&#x…...
17岁孩子开发AI应用，4个月入百万，人人都是AI产品经理的时代快来了
随着AI时代的到来叠加经济下行，越来越多的独立开发者梦想着实现年入百万的壮举。 近日，这种小概率事件正在发生。 17岁高中生做了个AI APP，短短四个月销售额达100 万美元。 小伙儿Zach Yadegari（下面暂称小扎克）在X…...
Django一分钟：DRF ViewSet烹饪指南，创建好用的视图集
本文将介绍django视图集的内部实现，并带你重写部分代码自己组装强大且趁手的视图集，以满足自定义的业务需求，避免编写大量重复代码。 一、基础知识 Django Rest framework框架允许你将一组相关视图的逻辑组合到一个类中，也就是我…...
SEO友好的wordpress模板 应该具体哪些特征
在数字营销的时代，搜索引擎优化(SEO)对于任何网站来说都是至关重要的。WordPress作为全球最受欢迎的内容管理系统之一，提供了大量的模板(也称为主题)供用户选择。一个SEO友好的WordPress模板不仅可以帮助您的网站在搜索引擎中获得更好的排名，…...
1.MySQL存储过程基础（1/10）
引言 数据库管理系统（Database Management System, DBMS）是现代信息技术中不可或缺的一部分。它提供了一种系统化的方法来创建、检索、更新和管理数据。DBMS的重要性体现在以下几个方面： 数据组织：DBMS 允许数据以结构化的方式存…...
linux中使用docker命令时提示权限不足
问题：成功安装docker后，使用docker相关命令时提示权限不足（permission denied） liubailiubai:~$ docker version Client: Version: 24.0.5 API version: 1.43 Go version: go1.20.14 Git commit: ced0996 Built: Tue Jun 25 22:3…...
Lucene最新最全面试题及参考答案
目录 Lucene主要功能及应用场景 Lucene 的索引结构是怎样的？ Lucene 中的 Segment 是如何工作的？ 如何在 Lucene 中实现文档的增删改查？ Lucene 中存储的数据类型有哪些？ 解释一下 Lucene 的索引过程。 Lucene 的搜索过程包含哪些步骤？ 什么是倒排索引？为什么它对…...
使用keras-tuner微调神经网络超参数
目录 随机搜索RandomSearch HyperBand 贝叶斯优化BayesianOptimization 附录 本文将介绍keras-tuner提供了三种神经网络超参数调优方法。它们分别是随机搜索RandomSearch、HyperBand和贝叶斯优化BayesianOptimization。 首先需要安装keras-tuner依赖库，安装命令如…...
【ECMAScript 从入门到进阶教程】第三部分：高级主题（高级函数与范式，元编程，正则表达式，性能优化）
第三部分：高级主题 第十章 高级函数与范式 在现代 JavaScript 开发中，高级函数与函数式编程范式正在逐渐成为开发者追求的目标。这种范式关注于函数的使用，消除副作用，提高代码的可读性和可维护性。 10.1. 高阶函数 高阶函数是…...
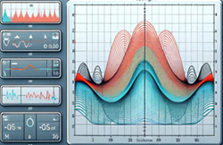
LabVIEW光偏振态检测系统
开发一套LabVIEW的高精度光偏振态检测系统，采用机械转动法结合光电探测器和高性能数据采集硬件，能快速、准确地测量光的偏振状态。该系统广泛应用于物理研究、激光技术和光学工业中。 系统组成 该光偏振态检测系统主要由以下硬件和软件模块构成…...
Linux线程（八）线程与信号之间的关系详解
本小节将对线程各方面的细节做深入讨论，其主要包括线程与信号之间牵扯的问题、线程与进程控制（fork()、exec()、exit()等）之间的交互。之所以出现了这些问题，其原因在于线程技术的问世晚于信号、进程控制等，然而线程的…...
红帽操作系统Linux基本命令2（ Linux 网络操作系统 06）
本文接着上篇Linux常用命令-1继续往后学习其他常用命令。 2.3 目录操作类命令 1．mkdir命令 mkdir命令用于创建一个目录。该命令的语法为： 上述目录名可以为相对路径，也可以为绝对路径。 mkdir命令的常用参数选项如下。 -p：在创…...
降重秘籍：如何利用ChatGPT将重复率从45%降至10%以下？
AIPaperGPT，论文写作神器~ https://www.aipapergpt.com/ 重复率高达45%？很多人一查论文的重复率，瞬间想“完了，这次真的要重写了”。但其实不用这么绝望！有了ChatGPT，降重真的没那么难。今天就教你几招&a…...
零门槛NAS搭建：WinNAS如何让普通电脑秒变私有云？
一、核心优势：专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发，是一款收费低廉但功能全面的Windows NAS工具，主打“无学习成本部署” 。与其他NAS软件相比，其优势在于： 无需硬件改造：将任意W…...
React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中，RouterProvider 是一个核心组件，用于提供基于数据路由（data routers）的新型路由方案。 它替代了传统的 <BrowserRouter>，支持更强大的数据加载和操作功能（如 loader 和…...
前端倒计时误差!
提示：记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来？二、五大解决方案1. 动态校准法（基础版）2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动（如演唱会、马拉松赛事、高考中考等）期间，城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例，暖城商圈曾因观众集中离场导致周边…...
【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台，覆盖应用全生命周期测试需求，主要提供五大核心能力： 测试类型检测目标关键指标功能体验基…...
.Net Framework 4/C# 关键字（非常用，持续更新...）
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容，如果兼容将返回 true，如果不兼容则返回 false，在进行类型转换前，可以先使用 is 关键字判断对象是否与指定类型兼容，如果兼容才进行转换，这样的转换是安全的。 例如有：首先创建一个字符串对象，然后将字符串对象隐…...
如何在网页里填写 PDF 表格？
有时候，你可能希望用户能在你的网站上填写 PDF 表单。然而，这件事并不简单，因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件，但原生并不支持编辑或填写它们。更糟的是，如果你想收集表单数据ÿ…...
华硕a豆14 Air香氛版，美学与科技的馨香融合
在快节奏的现代生活中，我们渴望一个能激发创想、愉悦感官的工作与生活伙伴，它不仅是冰冷的科技工具，更能触动我们内心深处的细腻情感。正是在这样的期许下，华硕a豆14 Air香氛版翩然而至，它以一种前所未有的方式&#x…...
Git常用命令完全指南：从入门到精通
Git常用命令完全指南：从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...