二叉树进阶--二叉搜索树
目录
1.二叉搜索树
1.1 二叉搜索树概念
1.2 二叉搜索树操作
1.3 二叉搜索树的实现
1.4 二叉搜索树的应用
1.5 二叉搜索树的性能分析
2.二叉树进阶经典题:
1.二叉搜索树
1.1 二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树
1.2 二叉搜索树操作
1. 二叉搜索树的查找a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。b、最多查找高度次,走到到空,还没找到,这个值不存在。2. 二叉搜索树的插入插入的具体过程如下:a. 树为空,则直接新增节点,赋值给root指针b. 树不空,按二叉搜索树性质查找插入位置,插入新节点3.二叉搜索树的删除首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:a. 要删除的结点无孩子结点b. 要删除的结点只有左孩子结点c. 要删除的结点只有右孩子结点d. 要删除的结点有左、右孩子结点删除方法:看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除
1.3 二叉搜索树的实现
这里使用递归版本和非递归版本进行实现,需要注意的是为了保证封装性,这里大多采用子函数的形式来防止封装性被破坏。其中删除的过程最复杂
//节点类
template <class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_key(key),_left(nullptr),_right(nullptr){}
};
//二叉搜索树
template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}//为了不破坏封装性,采用子函数的形式不暴露根BSTree(const BSTree<K>& t){_root = CopyTree(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root,t._root);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}//插入bool Insert(const K& key){//开始插入第一个的情况if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//不允许插入相同的值return false;}}cur = new Node(key);//判断链接的左右if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//查找bool Find(const K& key){if (_root == nullptr)return false;Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}//删除bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//找到了//1.可能是左为空//2.右为空//两边都不为空if(cur->_left == nullptr){//有可能删除根节点if (cur == _root){_root = _root->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){if (cur == _root){_root = _root->_right;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{//都不为空//从当前节点的右子树开始找最小的值Node* minright = cur->_right;Node* parent = cur;while (minright->_left){parent = minright;minright = minright->_left;}cur->_key = minright->_key;//将最小的值的节点剩下的节点链接给parentif (parent->_left == minright){parent->_left = minright->_right;}else{parent->_right = minright->_right;}delete minright;}return true;}}return false;}//打印,为了保证其封装性,可以使用子函数,采用中序遍历void Print(){PrintHelper(_root);}//递归版本的插入bool InsertR(const K& key){return _InsertR(_root, key);}//递归版本的查找bool FindR(const K& key){return _FindR(_root, key);}//递归版本的删除bool EraseR(const K& key){return _EraseR(_root, key);}
private:void Destroy(Node* root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}Node* CopyTree(Node* root){//前序建树即可if (root == nullptr){return true;}Node* newRoot = new Node(root->_key);newRoot->_left = CopyTree(root->_left);newRoot->_right = CopyTree(root->_right);return newRoot;}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{//找到,删除Node* del = root;//还是分3种情况if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{//在当前节点的右子树找到最小值,然后交换Node* minright = root->_right;while (minright->_left){minright = minright->_left;}//交换swap(minright->_key, root->_key);//在右子树中找到要删除的值return _EraseR(root->_right, key);}delete del;return true;}}bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return true;}}bool _InsertR(Node*& root,const K& key){if (root == nullptr){//插入,因为这里是引用,所以直接赋值即可root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{//相同return false;}}void PrintHelper(const Node* _root){//中序遍历if (_root == nullptr)return;PrintHelper(_root->_left);cout << _root->_key << " ";PrintHelper(_root->_right);}Node* _root = nullptr;
};1.4 二叉搜索树的应用
1. K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。2. KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
//改造二叉搜索树变为KV模型
namespace KV
{template <class K, class V>struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _val;BSTreeNode(const K& key, const V& val):_key(key), _val(val), _left(nullptr), _right(nullptr){}};template <class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public://插入bool Insert(const K& key, const V& val){//开始插入第一个的情况if (_root == nullptr){_root = new Node(key,val);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//不允许插入相同的值return false;}}cur = new Node(key,val);//判断链接的左右if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//查找Node* Find(const K& key){if (_root == nullptr)return nullptr;Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn cur;{}}return nullptr;}private:Node* _root = nullptr;};
}下面就是KV模型的两个例子:
1.在字典中查找你写的单词是否存在:
void TestBSTree1(){BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("tree", "树");dict.Insert("left", "左边、剩余");dict.Insert("right", "右边");dict.Insert("sort", "排序");string str;while (cin >> str){//在字典中查找BSTreeNode<string,string>* ret = dict.Find(str);if (ret){cout << ret->_val << endl;}else{cout << "不存在" << endl;}}}看看结果:
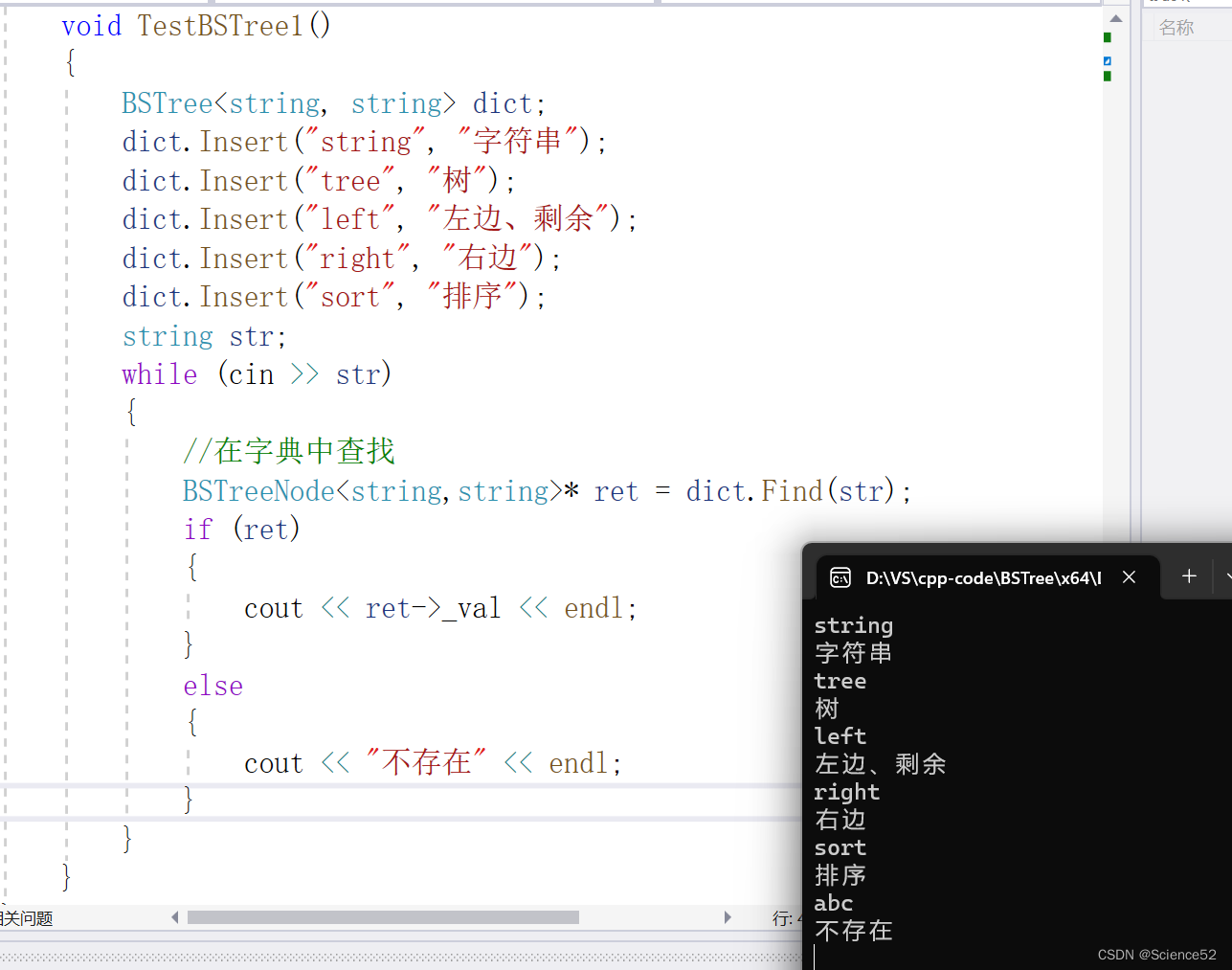
2.统计次数:(常用):
void TestBSTree2(){// 统计水果出现的次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (const auto& e : arr){//将数据插入到二叉搜索树中auto ret = countTree.Find(e);if (ret == nullptr){//树中没有该水果countTree.Insert(e, 1);}else{ret->_val++;}}countTree.Print();}结果:
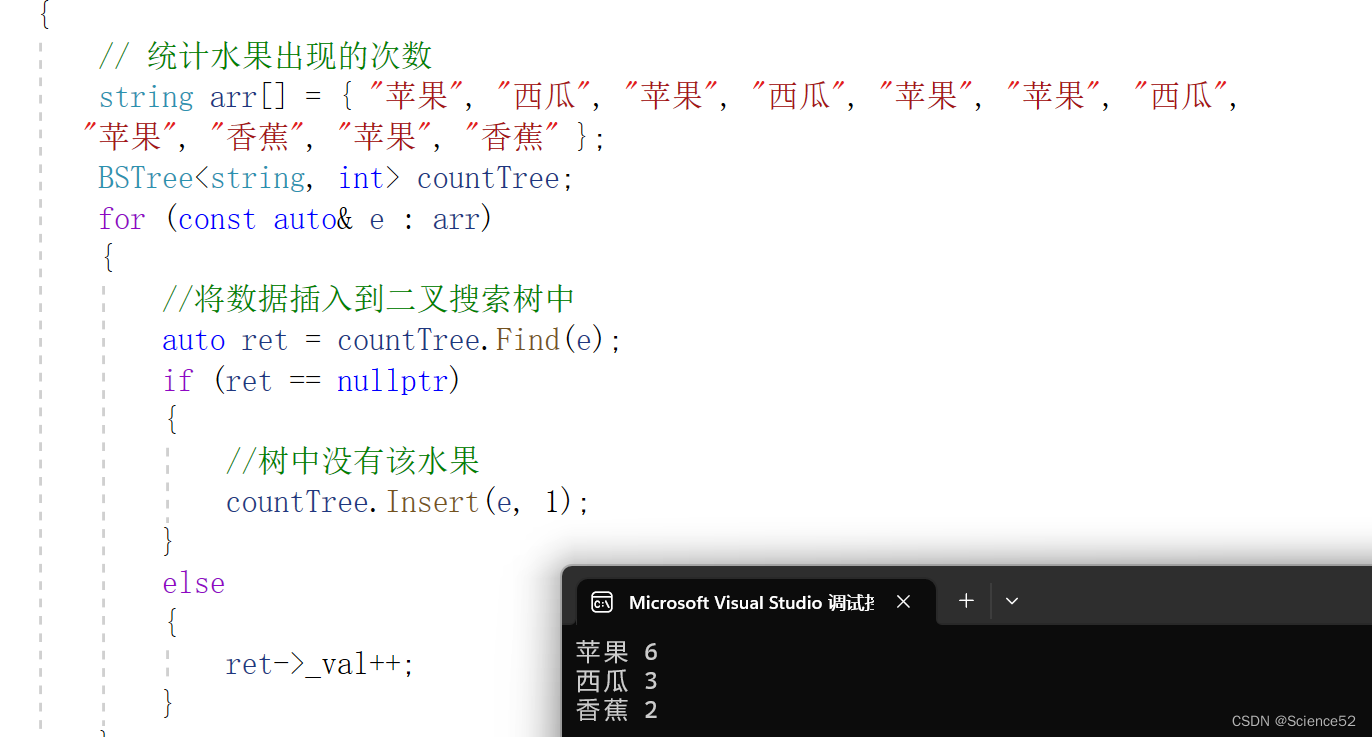
1.5 二叉搜索树的性能分析
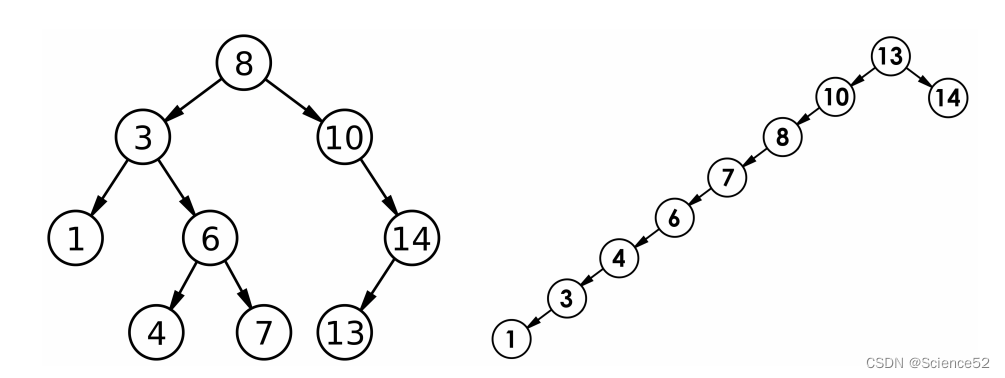
2.二叉树进阶经典题:
1.根据二叉树创建字符串
思路:根据前序遍历,我们可以通过根左子树右子树的顺序进行递归,但是递归子树的时候需要注意条件,如果左子树是空,但是有右子树就需要保留空括号,如果左子树不为空,但右子树为空,就不需要保留空括号。
class Solution {
public:void _tree2str(TreeNode* root,string& result){if(root == nullptr){result += "";return;}result += to_string(root->val);if(root->left || root->right){result += "(";_tree2str(root->left,result);result += ")";}if(root->right){result += "(";_tree2str(root->right,result);result += ")";}}string tree2str(TreeNode* root) {string result;_tree2str(root,result);return result;}
};2.二叉树的层序遍历
思路:我们可以通过队列来模拟层序遍历:一次输入一层的节点,然后把队列中当层的元素全部弹出,同时进入下一层元素,我们可以通过size来控制当层元素的个数。然后把当层元素放入结果集中
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;if(root == nullptr)return result;queue<TreeNode*> q;q.push(root);while(!q.empty()){vector<int> tmp;int size = q.size();while(size--){TreeNode* frontnode = q.front();q.pop();tmp.push_back(frontnode->val);//放入左右节点if(frontnode->left){q.push(frontnode->left);}if(frontnode->right){q.push(frontnode->right);}}result.push_back(tmp);}return result;}
};3.二叉树的最近公共祖先
思路:这题可以使用回溯法来解决,我们可以分别将p和q的路径存放在栈中,然后通过对栈的弹出操作,找到他们相同的节点。其中找路径问题就是回溯问题,我们可以把每次递归的结果先保存起来,如果找到就返回真,就可以结束递归,如果没有找到我们就继续递归,当子树递归到了nullptr时,我们就需要回退,回退的本质就是将栈顶元素pop。
class Solution {
public:bool _lowestCommonAncestor(TreeNode* root,TreeNode* p,stack<TreeNode*>& st){if(root == nullptr){return false;}st.push(root);if(root == p){return true;}if(_lowestCommonAncestor(root->left,p,st)){return true;}if(_lowestCommonAncestor(root->right,p,st)){return true;}//回退st.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//回溯法stack<TreeNode*> pv;stack<TreeNode*> qv;_lowestCommonAncestor(root,p,pv);_lowestCommonAncestor(root,q,qv);while(pv.size() != qv.size()){if(pv.size() > qv.size()){pv.pop();}elseqv.pop();}while(pv.top() != qv.top()){pv.pop();qv.pop();}return pv.top();}
};4.二叉搜索树与双向链表
思路:因为二叉搜索树的中序是有序的,我们可以先递归到最小的节点,然后通过中序改变它们之间的链接关系。
class Solution {
public:void _Convert(TreeNode* cur,TreeNode*& prev){if(cur == nullptr){return;}//中序走到最小_Convert(cur->left,prev);//建立链接关系//这里是防止第一次prev为空的情况if(prev){prev->right = cur;}cur->left = prev;prev = cur;_Convert(cur->right,prev);}TreeNode* Convert(TreeNode* root) {if(root == nullptr)return nullptr;TreeNode* prev = nullptr;_Convert(root,prev);//返回根while(root->left){root = root->left;}return root;}
};
5.从前序与中序遍历序列构造二叉树
思路:因为前序是可以确定根的,所以我们可以在中序中找到根,然后划分左右子树的区间,根据前序的顺序,先递归左子树,再递归右子树,当区间不存在时即可回退。
class Solution {
public:TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int begin,int end,int& i){if(begin > end)return nullptr;//从中序中找子树区间int j = begin;for(;j<=end;++j){if(inorder[j] == preorder[i])break;}TreeNode* root = new TreeNode(preorder[i++]);//[begin,j-1] j [j+1,end]root->left = _buildTree(preorder,inorder,begin,j-1,i);root->right = _buildTree(preorder,inorder,j+1,end,i);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {//先序找根,中序找子树//采用闭区间int i = 0;return _buildTree(preorder,inorder,0,inorder.size()-1,i);}
};6.使用非递归实现二叉树的前序遍历
思路:一般递归可以实现的代码,使用非递归都需要使用到数据结构的栈,我们可以将树分成左路节点和右树,我们先迭代左路节点到空,其中把每个值存放在栈中,并保存到结果集中,然后取栈顶元素再走右树即可。而中序遍历所需要保存的结果刚好是前序遍历栈弹出的结果,代码与这个类似。
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {//分成两部分,左路节点和右子树TreeNode* cur = root;stack<TreeNode*> st;vector<int> v;while(!st.empty() || cur){while(cur){v.push_back(cur->val);st.push(cur);cur = cur->left;}//走右子树TreeNode* tmp = st.top();st.pop();cur = tmp->right;}return v;}
};7.使用非递归实现二叉树的后序遍历
思路:这个和前序以及中序有所不同,就是在确定根的时候,我们需要确定两次,第一次是拿到根并走其右子树,第二次拿到根的时候就可以将根从栈中弹出了。我们也可以使用结构体存放每个节点和节点被取出的次数。当然还有更巧妙的方法:当我们走到右子树的最右端时,我们就可以使用一个指针记录下来,在当前节点回退的时候必然存在cur->right == prev(这个就是用来记录的节点),然后我们再把这个标记节点更新到当前节点,这样就可以不断回退了。具体看代码理解:
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> st;TreeNode* cur = root;TreeNode* prev = nullptr;//用来记录根的右子树是否被访问while(!st.empty() || cur){while(cur){st.push(cur);cur = cur->left;}TreeNode* top = st.top();//如果右子树为空或者到最右端返回的时候就回收结果if(top->right == nullptr || top->right == prev){st.pop();v.push_back(top->val);prev = top;//从最右端回来的时候起重要作用}else{//这时候要往右迭代cur = top->right;}}return v;}
};相关文章:

二叉树进阶--二叉搜索树
目录 1.二叉搜索树 1.1 二叉搜索树概念 1.2 二叉搜索树操作 1.3 二叉搜索树的实现 1.4 二叉搜索树的应用 1.5 二叉搜索树的性能分析 2.二叉树进阶经典题: 1.二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树,…...
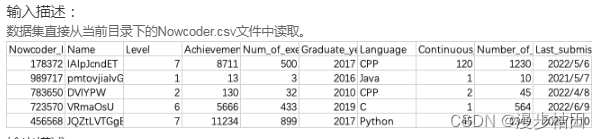
牛客网Python篇数据分析习题(三)
1.现有一个Nowcoder.csv文件,它记录了牛客网的部分用户数据,包含如下字段(字段与字段之间以逗号间隔): Nowcoder_ID:用户ID Level:等级 Achievement_value:成就值 Num_of_exercise&a…...

Java开发常见关键词集绵
一、关键词1: (1)RPC:远程过程调用(Remote Procedure Call)的缩写形式。远程调用的时候让人们觉得是本地调用。 (2)HTTP:超文本传输协议(Hyper Text Transfer…...
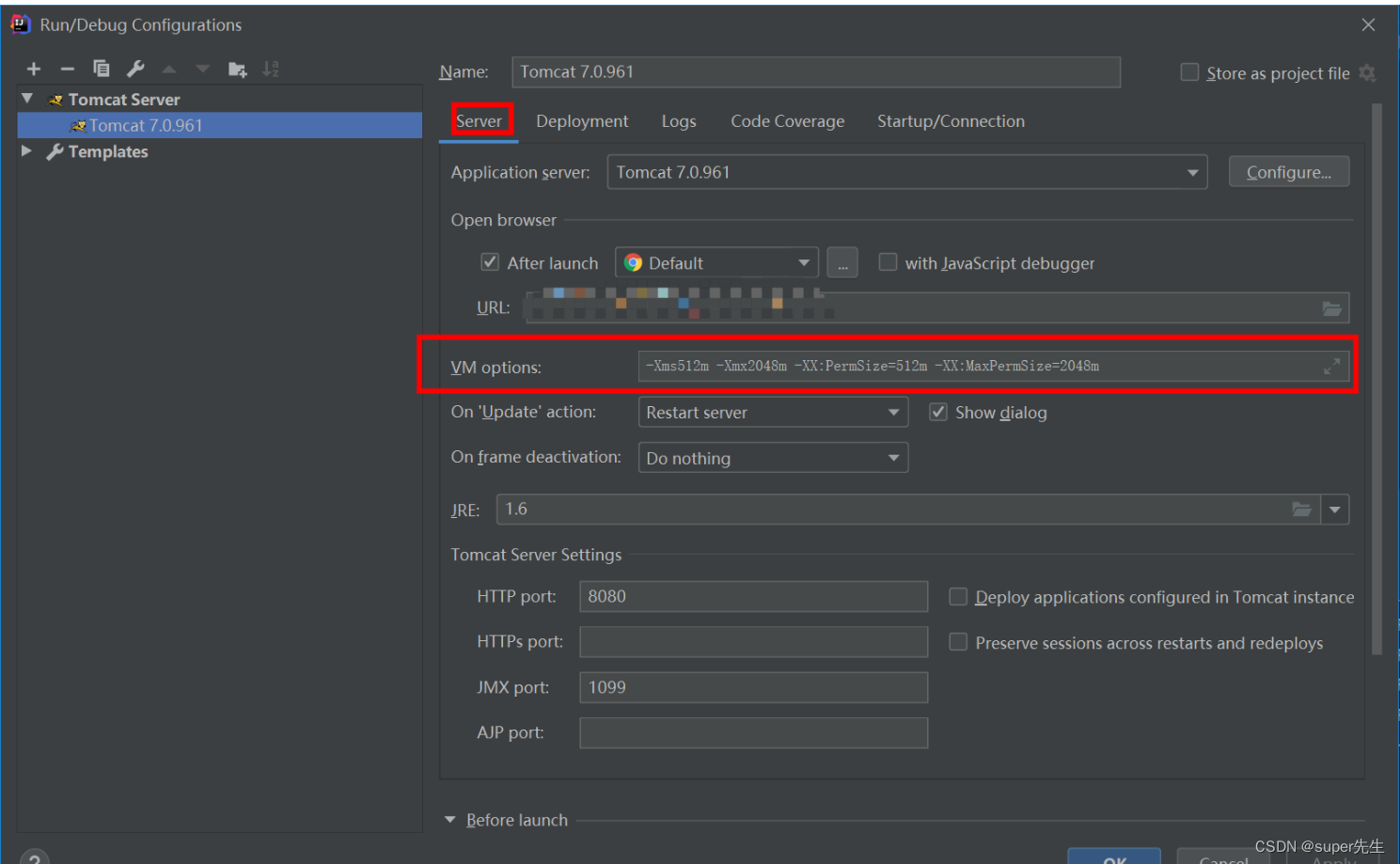
解决idea出现的java.lang.OutOfMemoryError: Java heap space的问题
文章目录1. 复现问题2. 分析问题3. 解决问题4. 补充解决java.lang.OutOfMemoryError: PermGen space问题1. 复现问题 今天使用idea开发时,突然报出如下错误: Exception in thread "main" java.lang.OutOfMemoryError: Java heap spaceat org.…...

为什么子进程要继承处理器亲缘性?
请先考虑一个典型的程序为什么需要启动一个子进程。(当然资源管理器不算一个典型的程序) 这是因为手头的任务被分解为子任务,无论出于何种原因,这些子任务都被放入子流程中。例如,在实现多次遍历型编译器/链接器时,其中每次遍历都…...

【算法】高精度
作者:指针不指南吗 专栏:算法篇 🐾不能只会思路,必须落实到代码上🐾 文章目录前言一、高精度加法二、高精度减法三、高精度乘法四、高精度除法前言 高精度即很大很大的数,超过了 long long 的范围&…...
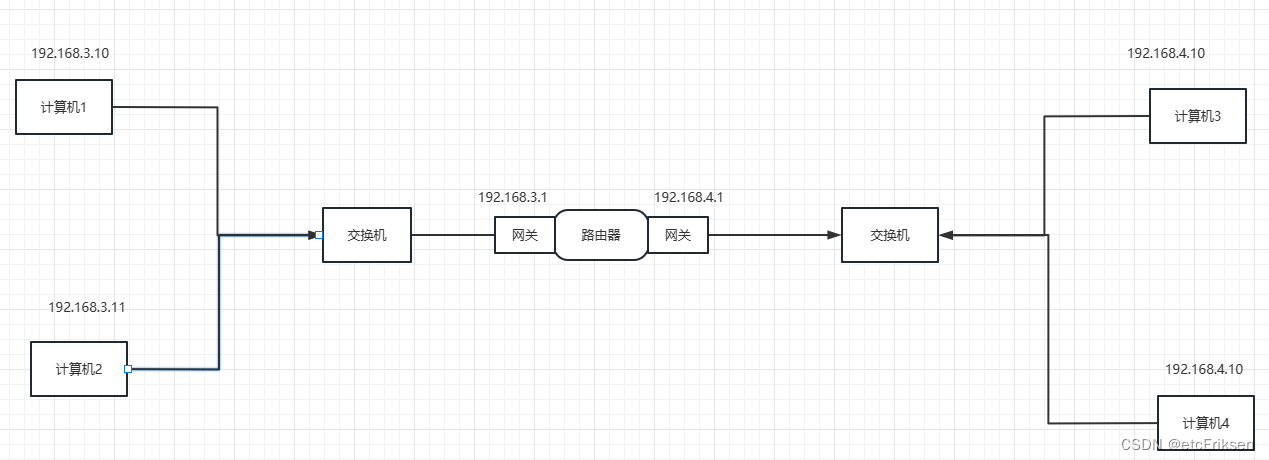
计算机网络-基本概念
目录 计算机网络-基本概念 互联网 Java的跨平台原理 编辑 C\C的跨平台原理 解释性语言的跨平台原理(python,js等) 客户端 vs 服务器 什么是协议? 网络互连模型 请求过程 计算机之间的通信基础 计算机之间的连接方式-网线直连(需要用交叉线,而…...

你评论,我赠书~【哈士奇赠书 - 13期】-〖Python程序设计-编程基础、Web开发及数据分析〗参与评论,即可有机获得
大家好,我是 哈士奇 ,一位工作了十年的"技术混子", 致力于为开发者赋能的UP主, 目前正在运营着 TFS_CLUB社区。 💬 人生格言:优于别人,并不高贵,真正的高贵应该是优于过去的自己。💬 ὎…...
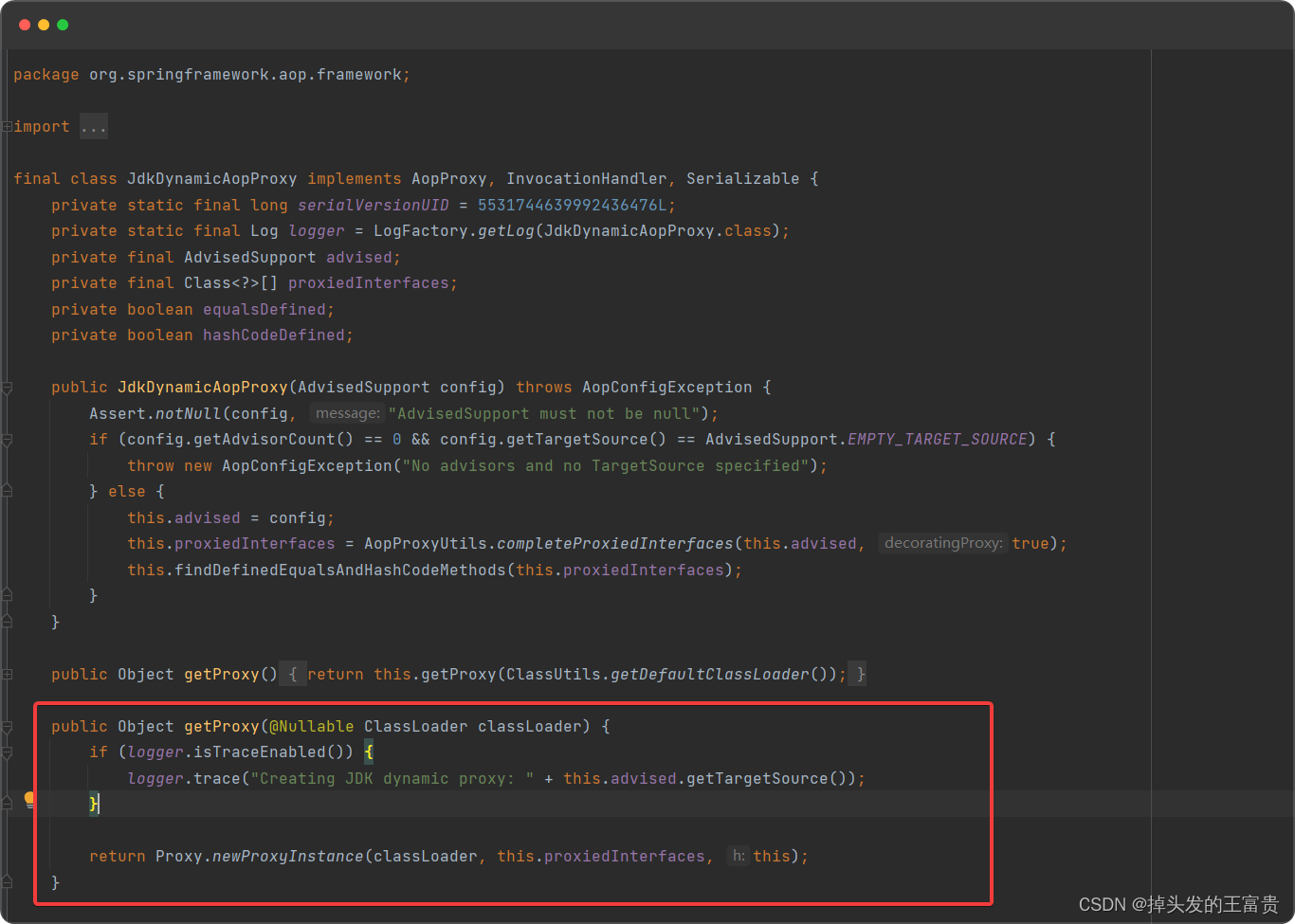
【设计模式】我终于读懂了代理模式。。。
👦代理模式的基本介绍 1)代理模式:为一个对象提供一个替身,以控制对这个对象的访问。即通过代理对象访问目标对象,这样做的好处是:可以在目标对象实现的基础上,增强额外的功能操作,即扩展目标对象的功能。 2)被代理的对象可以是远程对象、创建…...

每天10个前端小知识 【Day 2】
👩 个人主页:不爱吃糖的程序媛 🙋♂️ 作者简介:前端领域新星创作者、CSDN内容合伙人,专注于前端各领域技术,成长的路上共同学习共同进步,一起加油呀! ✨系列专栏:前端…...

帮助中心在线制作工具推荐这4款,很不错哟!
根据用户咨询问题是否解决的情景,分为三个部分,首先帮助中心恰好有用户需要咨询的问题,用户可以通过点击相关问题即可解决自己的问题,其次,用户第一眼没有在帮助中心解决问题,有个搜索框,用户的…...

rabbitMQ相关文章汇总
RabbitMQ五种工作模式: https://blog.csdn.net/weixin_41882200/article/details/117128590?ops_request_misc%257B%2522request%255Fid%2522%253A%2522167625223516800182771874%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id1…...

【C++】异常
🌈欢迎来到C专栏~~异常 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤…...
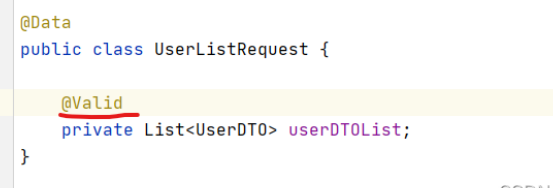
@Validated注解不生效问题汇总
Validated注解不生效问题汇总 文章目录Validated注解不生效问题汇总背景:一:可能原因原因1:原因2:原因3:原因4:二:补充全局异常对validation的处理背景: 项目框架应用的是validatio…...

华科万维C++章节练习2_4
题目:编写程序,从键盘输入一个字符,然后在屏幕上输出该字符开头的连续3个字符以及对应ASCII码。 输出格式请参看: 请输入一个字符>>A 字符 ASCII码 A 65 B 66 C 67 请按任意键继续. . . 请直接…...
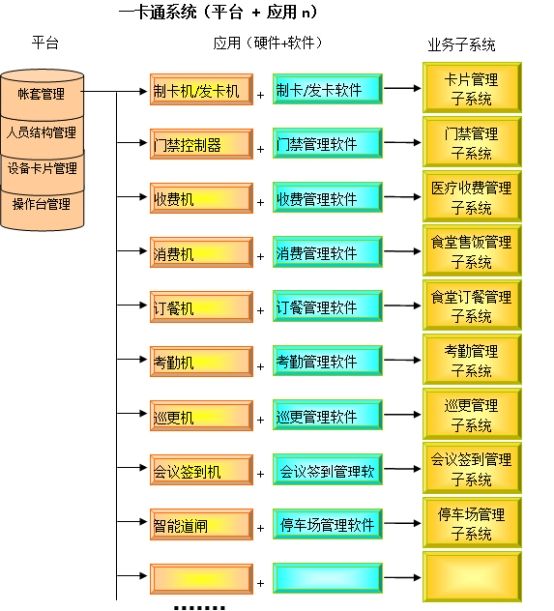
17万字数字化医院信息化建设大数据平台建设方案WORD
【版权声明】本资料来源网络,知识分享,仅供个人学习,请勿商用。【侵删致歉】如有侵权请联系小编,将在收到信息后第一时间删除!完整资料领取见文末,部分资料内容: 目录 第1章 医院信息化概述 1.…...

Android 11系统签名修改
Android OS 映像在两个地方使用加密签名:映像中的所有 .apk 文件都必须经过签名。Android 软件包管理器通过下列两种方式使用 .apk 签名:更换应用时,必须使用与旧应用相同的密钥对其签名,才能存取旧应用的数据。无论是通过覆盖 .a…...

亚马逊、沃尔玛卖家自养号退款经验和测评技术
今天给大家介绍下在做亚马逊、沃尔玛退款自养号中的经验,众所周知,自养号最重要的是养号的环境,包括系统的纯净度,下单的信用卡以及其他的一些细节。 环境系统市面上有很多,鱼龙混杂,比如什么lumi…...
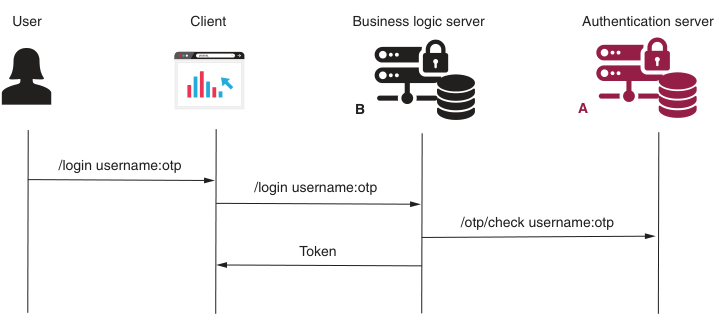
Spring Security in Action 第十一章 SpringSecurity前后端分离实战
本专栏将从基础开始,循序渐进,以实战为线索,逐步深入SpringSecurity相关知识相关知识,打造完整的SpringSecurity学习步骤,提升工程化编码能力和思维能力,写出高质量代码。希望大家都能够从中有所收获&#…...
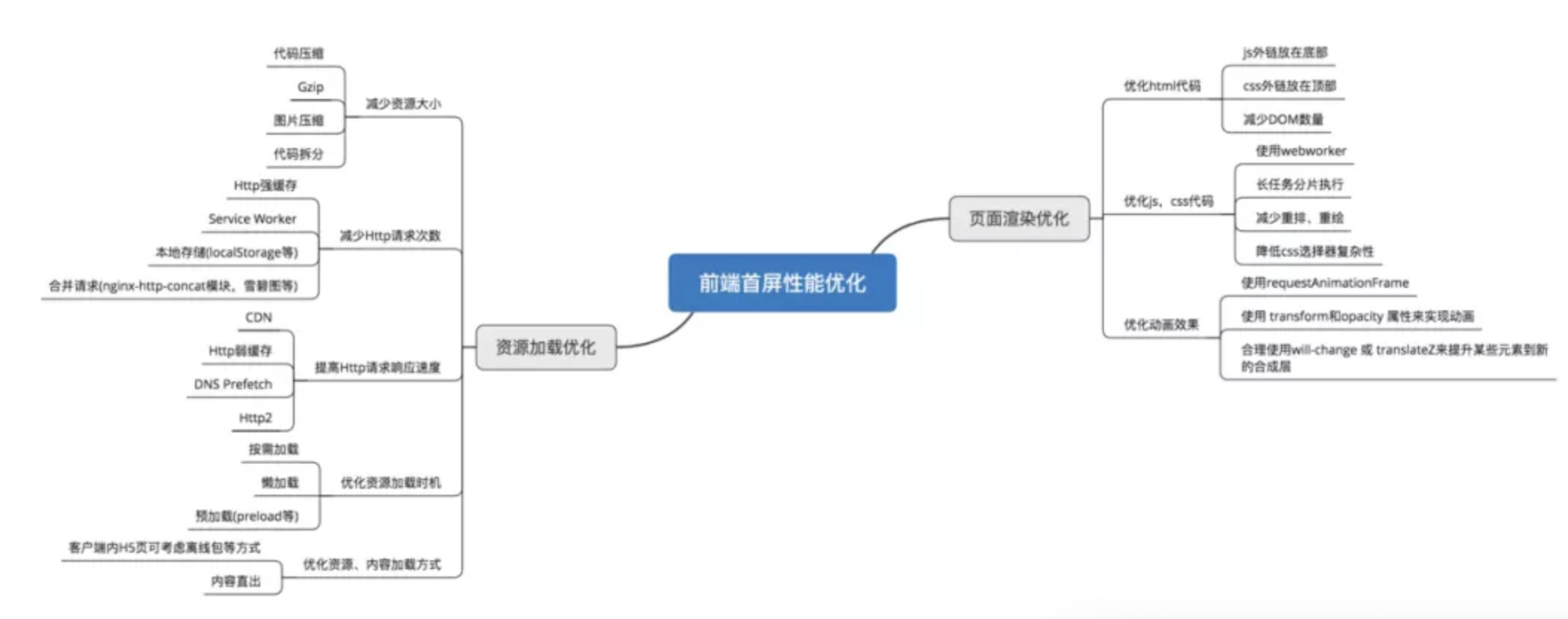
高级前端二面vue面试题(持续更新中)
action 与 mutation 的区别 mutation 是同步更新, $watch 严格模式下会报错 action 是异步操作,可以获取数据后调用 mutation 提交最终数据 MVVM的优缺点? 优点: 分离视图(View)和模型(Model)ÿ…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
