量子计算机的原理与物理实现
量子计算机的原理与物理实现很复杂
指导性原则
首先思考制备一台量子计算机需要些什么? 需要量子比特——二能级量子系统。除了量子计算机需要满足一些物理特性,它还必须要把量子比特绘制到某种初态上,以及测量系统的输出态。
而实验上的挑战在于,这些条件只能部分被满足。拿硬币正反两面举例,硬币是很糟糕的量子比特,因为其很难处于既表示正面又能表示反面的叠加态。核自旋或许可以实现,因为它可以长时间处于顺或逆外磁场的叠加态。但是从核自旋的方向构建量子计算机就很困难,因为它与周围粒子的耦合太弱,人们难以测量单个原子核的指向。
观察到相互抵触的约束是很普遍的:一台量子计算机必须被很好的孤立起来,以便维持它的量子特性,但又必须很好的被触及,因为需要测量其输出的状态。一个实际的实现在于如何维持这些脆弱的折衷。即困难不在于如何制造一台量子计算机,而在于量子计算机能被造的有多好 。
而什么样的物理系统有潜力成为处理量子信息的有些候选者呢?理解某种特定的量子计算机实现的优点的一个关键概念是量子噪声(有时候也被称为退相干(decoherence))。这个概念在之和的文章会介绍。破坏系统的既定演化过程——这是由于最长能允许的量子计算长度由和
的比值确定的,其中
是维持系统的相干性时间,
是完成一个酉运算的时间。在很多系统中,这两个时间实际上相互关联,它们都由系统与外部世界的耦合强度决定。
 量子计算的基本条件
量子计算的基本条件
1.稳定表示量子信息
2.完成一组通用的酉变换
3.制备基准初态
4.测量输出结果
量子信息的表示
量子计算基于量子态的变换。量子比特是一些二能级系统,作为量子计算机最简单的建造单元,它们为成对的量子态提供了方便的标志和物理实现。因此,比如自旋3/2的粒子的四个态,,
,
,
可以用来表示两个量子比特。
以计算作为目的,要实现的关键是可访问态的集合是有限的。沿一维直线运动的粒子的位置x通常不适合作为计算态的集合,尽管粒子可能处于量子态,乃至叠加态
。这是由于x处于概率上的连续区域,且具有无限大小的希尔伯特空间,因此无噪声时其信息容量也是无限的。而实际上噪声存在,会把可分态数目降到有限个。
实际上,通常需要把某些对称性献给态空间的有限性,以便把退相干降到最小。比如说,一个自旋1/2粒子的希尔伯特空间由和
两个态张成;自旋态不能处于此二维空间之外,当被很好的孤立后就会成为一个近乎完美的量子比特。
如果表示的不好就会退相干。譬如,一个处于有限深方势阱中的粒子,势阱深度足够容纳两个束缚态实现一个平庸的量子比特,因为从束缚态到连续非束缚态的跃迁有可能实现。这将导致退相干,因为会破坏量子比特的叠加态。对于单量子比特来说,质量指标是量子比特的最短寿命。用于自旋和原子系统的一个好的度量是,形如
的横弛豫时间,而纵弛豫时间T1(高能态)代表经典态的寿命。
方势阱和量子比特
有一个典型的量子系统,称为“方势阱”。指的是一个处于一维盒子中的粒子,其行为遵守薛定谔方程式,此系统的哈密顿量为,当0<x<L时V(x)=0,不在此区域V(x)=无穷。在位置空间基失波函数展开下的能量本征态为:
其中n为整数,,而
,这些态具有离散的能谱。定义任意波函数,
。由于
其中 。这个二能级系统表示一个量子比特
。该而能级系统表示一个量子比特,能否变换呢,这个量子比特会依据哈密顿量
随时间演化,对于V(x),可以附加扰动项效应。这展示了如何用一个方势阱中的最低两个能级代表量子比特,以及如何用势场的简单扰动对量子比特进行控制。但是扰动也会带来高阶效应,且在真实的物理系统中,盒子并非无限深,其他的能级进来,而能级就逐渐失效。另外实际上控制系统也是另外一个量子系统,而要与我们实现量子计算的系统相互耦合。这些问题导致了退相干。
执行酉运算
封闭系统由哈密顿量决定其酉运算,但是为了完成运算,得能控制哈密顿量,用一组通用的酉运算实现任意的选择,通过合理的控制和
,就能实现单自旋旋转。比如一个但自旋遵循哈密顿量
进行演化。
制备基本初态
通常只需能高保真制备一种特定的量子态,因为酉变换能把它变成任意的量子态。
测量输出结果
量子计算测量过程一个 重要的特性是波函数塌缩,它描述实施投影测量时发生了什么。一个优秀的量子算法输出是一个叠加态,对它进行测量时,会有很高的概率给出有用的答案。比如shor量子因式分解算法中的一步是从测量结果中找到在整数r。测量结果是一个靠近qc/r的整数,其中q是希尔伯特空间的维度。输出态实际上处于c所有可能值的等权叠加态,但是一次次测量将此态塌缩到一个随机的整数,因而能确保以很高概率确定r。
当然其中会遇到很多困难:光子探测器的效率太低,以及放大器热噪声都能使得测量产生误差,不仅如此,投影测量(强测量)通常难以实施,因为量子与经典系统的耦合太大,而且可关闭。
强测量不是必需的;连续地实施且从不关闭耦合的弱测量也可用于量子计算。当计算时间比测量短,且使用大量量子计算机系综时,就可以实现这点。这些系综一起给出的整体信号是一个宏观可观测量,并反映了量子态。
附录
1.什么是横弛豫时间和纵弛豫时间?
在量子计算中,单量子比特的质量指标通常包括其相干时间(包括纵向弛豫时间T1和横向弛豫时间T2)、门操作的保真度、以及量子比特的连通性等。其中,相干时间是衡量量子比特质量的一个重要指标,它描述了量子比特在不受干扰的情况下保持其量子状态的时间长度。量子比特的寿命,即相干时间,越长,意味着量子比特可以支持更多的量子操作,从而有能力执行更复杂的计算任务。
量子比特的寿命T1是指量子比特从高能级|1>衰变到低能级|0>的时间,用公式表示为(|1〉)=e^(-t/T1)。在未施加任何门操作的情况下,经过时间T1,量子比特仍处于|1>态的概率仅为1/e≈0.37。这意味着,量子比特的寿命越长,支持的有效操作的数量越多,即可以完成更复杂的运算。T1的测试方法包括将量子比特制备到|1>态上,等待一段时间t,对量子态进行测量,得到量子比特处于|1>态的概率P(|1〉),逐渐延长等待时间t,当P(|1〉)=1/e时,对应的等待时间t即为T1。
此外,量子比特还存在横向弛豫,即相干时间T2,它描述了量子比特状态在Bloch球面上xy平面出现角度偏移的时间,这种偏移最终会使量子比特从相干态退化为混合态。T2的测试方法包括将量子比特初始化到|0>态,经过一次Hadamard门操作,等待一段时间t,再施加一次Hadamard门操作,测量量子比特处于|0>态的概率P(|0〉),逐渐延长等待时间t,当P(|0〉)=1/e时,对应的等待时间t即为T2。
量子比特的门操作保真度也是一个重要的质量指标,它反映了量子比特执行计算操作的能力。量子比特门错误和量子比特门保真度是一对对应的概念,例如,1%的门错误率对应99%的门保真度,即每次对量子比特执行门操作时,成功率为99%。
相关文章:
量子计算机的原理与物理实现
量子计算机的原理与物理实现很复杂 指导性原则 首先思考制备一台量子计算机需要些什么? 需要量子比特——二能级量子系统。除了量子计算机需要满足一些物理特性,它还必须要把量子比特绘制到某种初态上,以及测量系统的输出态。 而实验上的挑战…...

SQL Server 常用关键词语法汇总
一、函数 1.1 CAST CAST ( expression AS data_type [ ( length ) ] )expression: 这是你想要转换的数据或表达式。data_type: 目标数据类型,比如 INT, VARCHAR, DATE 等等。(length): 对于某些数据类型(如 CHAR, VARCHAR, BINARY, VARBINARYÿ…...

软件测试工程师面试整理 —— 操作系统与网络基础!
在软件测试中,了解操作系统和网络基础知识对于有效地进行测试工作至关重要。无论是在配置测试环境、调试网络问题,还是在进行性能测试和安全测试时,这些知识都是不可或缺的。 1. 操作系统基础 操作系统(Operating System, OS&am…...

网络安全防御策略:通过限制IP访问提升服务器安全性
标题:网络安全防御策略:通过限制IP访问提升服务器安全性 摘要: 在网络安全领域,服务器被入侵是一场严重的事故。一旦发生这种情况,除了立即采取措施恢复系统外,还需要加强后续的安全防护措施。本文将探讨为…...

Multiprocessing出错没有提示was skipped without notice in python
这个问题可以通过打印返回结果解决。 解决方法 比如 Pool.apply_async(csdnKuangXiaoHU, args=(p, DestFile))改成 Result = Pool.apply_async(csdnKuangXiaoHU, args=...
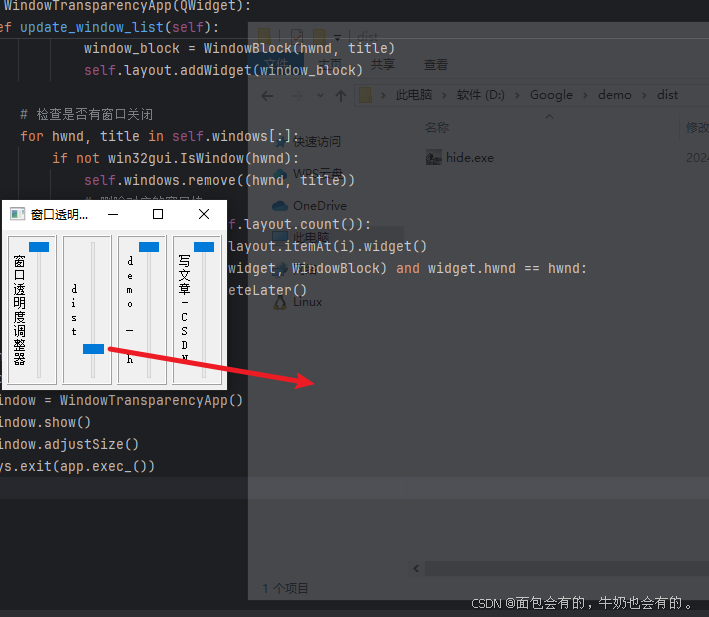
调整应用窗口透明度
朋友问我有没有软件透明得,一开始没理解,他给我发一个,我一看原来时调整窗口透明度得,想着python应该也可以实现,就写了一个。 效果图如下: 源码如下: import sys import ctypes from PySid…...

启智畅想集装箱号码智能识别原理,OCR识别应用
集装箱号码用途: 集装箱号码在填写托运单时是必填项,用于标识和跟踪货物运输过程中的集装箱。它有助于海关管理和物流跟踪,确保货物能够顺利通过海关检查并按时送达目的地。 集装箱号码智能识别原理: 在深入探讨集装箱号码OCR&…...

React基础知识
说明:react版本为 18.3.1 React是什么 React由Meta公司研发,是一个用于构建Web和原生交互界面的库。(开发基于浏览器的web应用和基于mac和android的移动应用)React的优势 1.相较于传统基于DOM开发的优势:组件化的开…...

Java基础:面向对象编程3
1 Java可变长参数 1.1 概述 Java 的可变长参数(Varargs)是在 Java 1.5 中引入的功能,允许方法接受任意数量的相同类型的参数。可变参数的语法是在参数类型后面加上三个点(...),例如 int... numbers。 1.…...

实验kubernetes的CPU绑定策略
CPU 管理配置 CPU 管理策略通过 kubelet 参数 --cpu-manager-policy 或 KubeletConfiguration 中的 cpuManagerPolicy 字段来指定。 支持两种策略: none:默认策略。static:允许为节点上具有某些资源特征的 Pod 赋予增强的 CPU 亲和性和独占…...

Zsh 安装与配置
目录 1 环境配置 1.1 基本工具安装 1.2 安装 oh-my-zsh 1.3 从.bashrc中迁移配置(可选) 2 主题配置 2.1 内置主题 2.2 自定义主题 2.2.1 推荐主题 3 插件安装 3.1 推荐插件 3.1.1 zsh -autosuggestions 3.1.2 zsh-syntax-highlighting 3.2 启…...

Redis可视化工具Redis Desktop Manager(附安装包)
前言 redis工具,我相信每个开发都需要,如果每次查都去client执行指令,我怕查完之后,老大就要发版咯。我之前一直用的Redis可视化工具RedisDesktopManager,总觉得差点意思,直到同事推荐了个新的,…...

sql server删除过期备份文件脚本
一、通过脚本查看过期文件,时间可以自己设定 for /f "delims" %i in (dir /b /a-d "E:\mybak_file\*.bak" ^| findstr /i "backup" ^| findstr /v /i "no_backup") do if "%~ti" LSS "2024/09/29 16:50&qu…...

【Docker系列】Docker查看镜像架构
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

Python案例 | 测试网络的下载速度上传速度和 ping 延迟
使用了 speedtest 库来测试网络的下载速度上传速度和 ping 延迟 注意,这里需要先卸载speedtest,再安装speedtest-cli pip uninstall speedtest pip install speedtest-cli其次运行代码: # 使用了 speedtest 库来测试网络的下载速度上传速度…...

一键找回,2024四大固态硬盘数据恢复工具推荐!
虽然固态硬盘(SSD)因其读写速度快、功耗低等特点受到广泛欢迎,但它并非无懈可击,数据丢失的问题依然存在。如果你也遇到了固态硬盘数据丢失的问题,那么一下的这几款软件可以一试! 福昕数据恢复 直达链接&…...

数据结构~AVL树
文章目录 一、AVL树的概念二、AVL树的定义三、AVL树的插入四、AVL树的平衡五、AVL树的验证六、AVL树的删除七、完整代码八、总结 一、AVL树的概念 AVL树是最先发明的自平衡二叉查找树,AVL是⼀颗空树,或者具备下列性质的二叉搜索树:它的左右子…...

ffmpeg面向对象——rtsp拉流探索(1)
目录 0.avformat_open_input的rtsp流程程纯净版1.rtsp拉流流程图2.rtsp拉流对象图 标准rtsp协议的基石是tcp,本节探索下ffmpeg的rtsp拉流协议tcp的创建及rtsp协商过程。 0.avformat_open_input的rtsp流程程纯净版 ffmpeg拉流,从avformat_open_input接口…...

【启明智显分享】ZX7981PM WIFI6 5G-CPE:2.5G WAN口,2.4G/5G双频段自动调速
昨天,我们向大家展现了ZX7981PG WIFI6 5G-CPE,它强大的性能也引起了一波关注,与此同时,我们了解到部分用户对更高容量与更高速网口的需求。没关系!启明智显早就预料到了!ZX7981PM满足你的需求! …...

openresty“热部署“lua
一、前言 频繁reload 或者restart影响测试使用nginx,修改lua脚本后要实际查看效果值,使用关闭lua代码缓存,可以实现实时查看代码效果。 每次请求都会从磁盘中加载lua脚本,生产上面不要开启,影响响应速度 二、修改ngin…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
