【【自动驾驶】车辆运动学模型】
【自动驾驶】车辆运动学模型
- 1. 引言
- 2. 以车辆重心为中心的单车模型
- 2.1 模型介绍
- 2.2 滑移角 β \beta β 的推导
- 2.2 航向角 ψ \psi ψ推导过程:
- 2.3 滑移角 β \beta β
- 2.3 Python代码实现
- 2.4 C++代码实现
- 3. 前轮驱动的单车模型
- 3.1 模型介绍
- 3.3 Python代码实现
- 3.4 C++代码实现
- 4. 以后轴中心为车辆中心的单车模型
- 4.1 模型介绍
- 4.3 Python代码实现
- 4.4 C++代码实现
- 5. 阿克曼转向几何
- 5.1 模型介绍
- 5.2 滑移角 β \beta β 的推导
- 5.3 Python代码实现
- 5.4 C++代码实现
- 6. 总结
- 参考资料

1. 引言
在自动驾驶技术的发展过程中,对车辆运动的理解和建模至关重要。车辆运动学模型用于描述车辆的运动特性,尤其是在低速条件下,通过控制输入来预测车辆的未来状态。本文将详细介绍几种常见的车辆运动学模型,并提供Python和C++的代码实现。
好的,我们将详细推导并更新其他模型中的侧滑角 β \beta β。以下是每个模型的详细推导和代码实现。
2. 以车辆重心为中心的单车模型
2.1 模型介绍
在自动驾驶领域,通常采用单车模型来简化实际车辆的复杂性。此模型将车辆视为具有两个转动轴的刚体,即前轮和后轮,每个轴上的左右轮合并为一个轮子来考虑。模型的关键参数包括:

- 车辆重心:点C,代表车辆的质量中心。
- 前后轮距离: l f l_f lf 和 l r l_r lr 分别从前轮中心到重心的距离和从后轮中心到重心的距离。
- 轴距: L = l f + l r L = l_f + l_r L=lf+lr。
- 速度: V V V,表示车辆重心的速度。
- 滑移角: β \beta β,车辆速度矢量与车辆纵向轴之间的夹角。
- 航向角: ψ \psi ψ,车身与X轴的夹角。
- 转向角: δ f \delta_f δf 和 δ r \delta_r δr,分别表示前轮和后轮的转向角。对于大多数车辆, δ r \delta_r δr 可以设置为0。
2.2 滑移角 β \beta β 的推导
- 几何关系:
- 假设车辆的重心位于点C,前轮中心位于点F,后轮中心位于点R。
- 前轮的转向角 δ f \delta_f δf 导致前轮的行驶方向与车辆纵向轴之间有一个夹角。
- 后轮的转向角 δ r \delta_r δr 导致后轮的行驶方向与车辆纵向轴之间有一个夹角。
2.2 航向角 ψ \psi ψ推导过程:
- 如上图所示,在三角形 O C A O C A OCA中,根据正弦定理,有:
s i n ( δ f − β ) l f = s i n ( π 2 − δ f ) R (1) \frac{sin(\delta_f - \beta)}{l_f} = \frac{sin(\frac{\pi}{2} - \delta_f)}{R} \tag{1} lfsin(δf−β)=Rsin(2π−δf)(1) - 在三角形 O B C OBC OBC中,根据正弦定理,有:
s i n ( β − δ r ) l r = s i n ( π 2 + δ r ) R (2) \frac{sin(\beta - \delta_r)}{l_r} = \frac{sin(\frac{\pi}{2}+ \delta_r)}{R} \tag{2} lrsin(β−δr)=Rsin(2π+δr)(2) - 化简:
s i n ( δ f ) c o s ( β ) − s i n ( β ) c o s ( δ f ) l f = c o s ( δ f ) R (3) \frac{sin(\delta_f)cos(\beta) - sin(\beta)cos(\delta_f)}{l_f} = \frac{cos(\delta_f)}{R} \tag{3} lfsin(δf)cos(β)−sin(β)cos(δf)=Rcos(δf)(3)
s i n ( β ) c o s ( δ r ) − s i n ( δ r ) c o s ( β ) l r = c o s ( δ r ) R (4) \frac{sin(\beta)cos(\delta_r) - sin(\delta_r)cos(\beta)}{l_r} = \frac{cos(\delta_r)}{R} \tag{4} lrsin(β)cos(δr)−sin(δr)cos(β)=Rcos(δr)(4)
等式(3)两边同乘以 l f c o s ( δ f ) \frac{l_f}{cos(\delta_f)} cos(δf)lf:
s i n ( δ f ) c o s ( β ) − s i n ( β ) c o s ( δ f ) = l f c o s ( δ f ) R (5) sin(\delta_f)cos(\beta) - sin(\beta)cos(\delta_f) = \frac{l_fcos(\delta_f)}{R} \tag{5} sin(δf)cos(β)−sin(β)cos(δf)=Rlfcos(δf)(5)
同理等式(4)两边同乘以 l r l_r lr:
s i n ( β ) c o s ( δ r ) − s i n ( δ r ) c o s ( β ) = l r c o s ( δ r ) R (6) sin(\beta)cos(\delta_r) - sin(\delta_r)cos(\beta) = \frac{l_rcos(\delta_r)}{R} \tag{6} sin(β)cos(δr)−sin(δr)cos(β)=Rlrcos(δr)(6)
(5)(6)两式相加:
c o s ( β ) ( s i n ( δ f ) − s i n ( δ r ) ) = l r + l f R (7) cos(\beta)(sin(\delta_f)-sin(\delta_r)) = \frac{l_r +l_f}{R} \tag{7} cos(β)(sin(δf)−sin(δr))=Rlr+lf(7)
根据条件假设,低速环境下,车辆行驶路径的转弯半径变化缓慢,此时我们可以假设车辆偏航角的变化率 ψ ˙ \dot{\psi} ψ˙
可近似等于车辆的角速度 ω \omega ω。根据车辆角速度 ω = V R \omega = \frac{V}{R} ω=RV得:
ψ ˙ = ω = V R (8) \dot{\psi} = \omega = \frac{V}{R} \tag{8} ψ˙=ω=RV(8)
将(8)带入(7)中,消除 R R R得:
ψ ˙ = V c o s ( β ) l r + l f ( t a n ( δ f ) − t a n ( δ r ) ) (9) \dot{\psi}= \frac{Vcos(\beta)}{l_r +l_f}(tan(\delta_f)-tan(\delta_r)) \tag{9} ψ˙=lr+lfVcos(β)(tan(δf)−tan(δr))(9)
2.3 滑移角 β \beta β
- 滑移角 β \beta β 定义为车辆速度矢量与车辆纵向轴之间的夹角。
- 当车辆转弯时,前轮和后轮的速度矢量会有所不同,导致车辆重心的速度矢量与车辆纵向轴之间有一个夹角。
等式(5)两边同乘以 l r l_r lr:
l r ( t a n ( δ f ) c o s ( β ) − s i n ( β ) − l f l r R (10) l_r(tan(\delta_f)cos(\beta)-sin(\beta) - \frac{l_f l_r}{R} \tag{10} lr(tan(δf)cos(β)−sin(β)−Rlflr(10)
同理等式(6)两边同乘以 l f l_f lf:
l f ( s i n ( β ) − t a n ( δ r ) c o s ( β ) ) = l f l r R (11) l_f(sin(\beta) - tan(\delta_r)cos(\beta)) = \frac{l_f l_r}{R} \tag{11} lf(sin(β)−tan(δr)cos(β))=Rlflr(11)
(10)(11)两式相等:
c o s ( β ) ( l r t a n ( δ f ) + l f t a n ( δ r ) ) = s i n ( β ) ( l r + l f ) (12) cos(\beta)(l_r tan(\delta_f) + l_f tan(\delta_r)) =sin(\beta)(l_r +l_f) \tag{12} cos(β)(lrtan(δf)+lftan(δr))=sin(β)(lr+lf)(12)
合并 t a n ( β ) tan(\beta) tan(β):
t a n ( β ) = l r t a n ( δ f ) + l f t a n ( δ r ) l r + l f (13) tan(\beta) = \frac{l_r tan(\delta_f) + l_f tan(\delta_r)}{l_r +l_f} \tag{13} tan(β)=lr+lflrtan(δf)+lftan(δr)(13)
车辆运动学模型
{ x ˙ = V cos ( ψ + β ) y ˙ = V sin ( ψ + β ) ψ ˙ = V c o s ( β ) l r + l f ( t a n ( δ f ) − t a n ( δ r ) ) (14) \left\{ \begin{array}{l} \dot{x} = V \cos (\psi + \beta) \\ \dot{y} = V \sin (\psi + \beta) \\ \dot{\psi} = \frac{Vcos(\beta)}{l_r +l_f}(tan(\delta_f)-tan(\delta_r)) \end{array} \right. \tag{14} ⎩ ⎨ ⎧x˙=Vcos(ψ+β)y˙=Vsin(ψ+β)ψ˙=lr+lfVcos(β)(tan(δf)−tan(δr))(14)
其中
β = a r c t a n ( l r t a n ( δ f ) + l f t a n ( δ r ) l r + l f ) (15) \beta = arctan(\frac{l_r tan(\delta_f) + l_f tan(\delta_r)}{l_r +l_f} \tag{15}) β=arctan(lr+lflrtan(δf)+lftan(δr))(15)
2.3 Python代码实现
import mathclass KinematicModel_1:def __init__(self, x, y, psi, v, l_r, l_f, dt):self.x = xself.y = yself.psi = psiself.v = vself.l_f = l_fself.l_r = l_rself.dt = dtdef update_state(self, a, delta_f, delta_r=0):# 计算滑移角 βbeta = math.atan2(self.l_r * math.sin(delta_f) + self.l_f * math.sin(delta_r),self.l_r * math.cos(delta_f) + self.l_f * math.cos(delta_r))# 更新状态self.x += self.v * math.cos(self.psi + beta) * self.dtself.y += self.v * math.sin(self.psi + beta) * self.dtself.psi += (self.v / (self.l_f + self.l_r)) * (math.tan(delta_f) - math.tan(delta_r)) * math.cos(beta) * self.dtself.v += a * self.dtdef get_state(self):return self.x, self.y, self.psi, self.v
2.4 C++代码实现
#include <cmath>
#include <iostream>class KinematicModel_1 {
public:KinematicModel_1(double x, double y, double psi, double v, double l_r, double l_f, double dt) :x(x), y(y), psi(psi), v(v), l_f(l_f), l_r(l_r), dt(dt) {}void update_state(double a, double delta_f, double delta_r = 0) {// 计算滑移角 βdouble beta = atan2(l_r * sin(delta_f) + l_f * sin(delta_r),l_r + l_f );// 更新状态x += v * cos(psi + beta) * dt;y += v * sin(psi + beta) * dt;psi += (v / (l_f + l_r)) * (tan(delta_f) - tan(delta_r)) * cos(beta) * dt;v += a * dt;}void get_state() const {std::cout << "x: " << x << ", y: " << y << ", psi: " << psi << ", v: " << v << std::endl;}private:double x, y, psi, v, l_f, l_r, dt;
};
3. 前轮驱动的单车模型
3.1 模型介绍
当仅考虑前轮转向时,模型可以简化为:

车辆运动学模型
{ x ˙ = V cos ( ψ + β ) y ˙ = V sin ( ψ + β ) ψ ˙ = V sin β l r (16) \left\{ \begin{array}{l} \dot{x} = V \cos (\psi + \beta) \\ \dot{y} = V \sin (\psi + \beta) \\ \dot{\psi} = \frac{V \sin \beta}{l_r} \end{array} \right. \tag{16} ⎩ ⎨ ⎧x˙=Vcos(ψ+β)y˙=Vsin(ψ+β)ψ˙=lrVsinβ(16)
其中 δ r = 0 \delta_r = 0 δr=0,滑移角 β \beta β 可以表示为:
β = arctan ( l r l f + l r tan ( δ f ) ) (17) \beta = \arctan \left( \frac{l_r}{l_f + l_r} \tan(\delta_f) \right) \tag{17} β=arctan(lf+lrlrtan(δf))(17)
3.3 Python代码实现
class KinematicModel_2:def __init__(self, x, y, psi, v, l_r, l_f, dt):self.x = xself.y = yself.psi = psiself.v = vself.l_f = l_fself.l_r = l_rself.dt = dtdef update_state(self, a, delta_f):# 计算滑移角 βbeta = math.atan((self.l_r / (self.l_f + self.l_r)) * math.tan(delta_f))# 更新状态self.x += self.v * math.cos(self.psi + beta) * self.dtself.y += self.v * math.sin(self.psi + beta) * self.dtself.psi += (self.v * math.sin(beta) / self.l_r) * self.dtself.v += a * self.dtdef get_state(self):return self.x, self.y, self.psi, self.v
3.4 C++代码实现
class KinematicModel_2 {
public:KinematicModel_2(double x, double y, double psi, double v, double l_r, double l_f, double dt) :x(x), y(y), psi(psi), v(v), l_f(l_f), l_r(l_r), dt(dt) {}void update_state(double a, double delta_f) {// 计算滑移角 βdouble beta = atan((l_r / (l_f + l_r)) * tan(delta_f));// 更新状态x += v * cos(psi + beta) * dt;y += v * sin(psi + beta) * dt;psi += (v * sin(beta) / l_r) * dt;v += a * dt;}void get_state() const {std::cout << "x: " << x << ", y: " << y << ", psi: " << psi << ", v: " << v << std::endl;}private:double x, y, psi, v, l_f, l_r, dt;
};
4. 以后轴中心为车辆中心的单车模型
4.1 模型介绍
当以车辆后轴中心为参考点时,模型可以进一步简化。假设后轮没有转向角( δ r = 0 \delta_r = 0 δr=0),模型可以表示为:

{ x ˙ = V cos ( ψ ) y ˙ = V sin ( ψ ) ψ ˙ = V L tan δ f (18) \left\{ \begin{array}{l} \dot{x} = V \cos (\psi) \\ \dot{y} = V \sin (\psi) \\ \dot{\psi} = \frac{V}{L} \tan \delta_f \end{array} \right. \tag{18} ⎩ ⎨ ⎧x˙=Vcos(ψ)y˙=Vsin(ψ)ψ˙=LVtanδf(18)
其中, L L L 是轴距, δ f \delta_f δf 是前轮转向角。
- 在这种模型中,滑移角 β \beta β 可以近似为0,因为重心位于后轴中心,且后轮没有转向角。
- 因此,滑移角 β \beta β 可以表示为:
β ≈ 0 \beta \approx 0 β≈0
4.3 Python代码实现
class KinematicModel_3:def __init__(self, x, y, psi, v, L, dt):self.x = xself.y = yself.psi = psiself.v = vself.L = Lself.dt = dtdef update_state(self, a, delta_f):# 更新状态self.x += self.v * math.cos(self.psi) * self.dtself.y += self.v * math.sin(self.psi) * self.dtself.psi += (self.v / self.L) * math.tan(delta_f) * self.dtself.v += a * self.dtdef get_state(self):return self.x, self.y, self.psi, self.v
4.4 C++代码实现
class KinematicModel_3 {
public:KinematicModel_3(double x, double y, double psi, double v, double L, double dt) :x(x), y(y), psi(psi), v(v), L(L), dt(dt) {}void update_state(double a, double delta_f) {// 更新状态x += v * cos(psi) * dt;y += v * sin(psi) * dt;psi += (v / L) * tan(delta_f) * dt;v += a * dt;}void get_state() const {std::cout << "x: " << x << ", y: " << y << ", psi: " << psi << ", v: " << v << std::endl;}private:double x, y, psi, v, L, dt;
};
5. 阿克曼转向几何
5.1 模型介绍
阿克曼转向几何(Ackerman Turning Geometry)是一种为了解决交通工具转弯时,内外转向轮路径指向的圆心不同的几何学。在单车模型中,将转向时左、右前轮偏角假设为同一角度 δ f \delta_f δf,虽然通常两个角度大致相等,但实际并不是,通常情况下,内侧轮胎转角更大。

- 外轮转角: δ o = L R + l w 2 \delta_o = \frac{L}{R + \frac{l_w}{2}} δo=R+2lwL
- 内轮转角: δ i = L R − l w 2 \delta_i = \frac{L}{R - \frac{l_w}{2}} δi=R−2lwL
其中, l w l_w lw 为轮距, R R R 为轨迹半径。
5.2 滑移角 β \beta β 的推导
-
几何关系:
- 车辆转弯时,内外轮的轨迹半径不同。
- 外轮的轨迹半径为 R + l w 2 R + \frac{l_w}{2} R+2lw。
- 内轮的轨迹半径为 R − l w 2 R - \frac{l_w}{2} R−2lw。
-
转向角计算:
- 外轮转角 δ o \delta_o δo 可以表示为:
δ o = L R + l w 2 (19) \delta_o = \frac{L}{R + \frac{l_w}{2}} \tag{19} δo=R+2lwL(19) - 内轮转角 δ i \delta_i δi 可以表示为:
δ i = L R − l w 2 (20) \delta_i = \frac{L}{R - \frac{l_w}{2}} \tag{20} δi=R−2lwL(20)
- 外轮转角 δ o \delta_o δo 可以表示为:
-
滑移角 β \beta β 的计算:
- 在阿克曼转向几何中,滑移角 β \beta β 主要取决于车辆的几何参数和转向角。
- 通常情况下,滑移角 β \beta β 可以近似为0,因为阿克曼转向几何设计使得内外轮的转向角能够很好地匹配车辆的转弯半径。
5.3 Python代码实现
class AckermannSteering:def __init__(self, L, l_w, R):self.L = Lself.l_w = l_wself.R = Rdef calculate_steering_angles(self, delta_f):delta_o = self.L / (self.R + self.l_w / 2)delta_i = self.L / (self.R - self.l_w / 2)return delta_o, delta_i
5.4 C++代码实现
#include <cmath>
#include <iostream>class AckermannSteering {
public:AckermannSteering(double L, double l_w, double R) : L(L), l_w(l_w), R(R) {}std::pair<double, double> calculate_steering_angles(double delta_f) {double delta_o = L / (R + l_w / 2);double delta_i = L / (R - l_w / 2);return {delta_o, delta_i};}private:double L, l_w, R;
};
6. 总结
本文详细介绍了车辆运动学模型的基本概念,并提供了Python和C++的实现代码。通过这些模型,我们可以更好地理解车辆在不同控制输入下的运动行为,这对于开发自动驾驶系统的控制策略至关重要。希望本文能够为自动驾驶领域的研究者和开发者提供有价值的参考。
参考资料
- 【自动驾驶】车辆运动学模型 - CSDN博客
以上就是《【自动驾驶】车辆运动学模型》的全部内容,希望能够帮助到你。如果你有任何疑问或者建议,欢迎留言交流!
相关文章:

【【自动驾驶】车辆运动学模型】
【自动驾驶】车辆运动学模型 1. 引言2. 以车辆重心为中心的单车模型2.1 模型介绍2.2 滑移角 β \beta β 的推导2.2 航向角 ψ \psi ψ推导过程:2.3 滑移角 β \beta β2.3 Python代码实现2.4 C代码实现 3. 前轮驱动的单车模型3.1 模型介绍3.3 Python代码实现3.4 …...

叉尖避障新科技:因泰立科技ILS-T52三维深度成像激光雷达
ILS-T52三维深度成像激光雷达是一款高性能的纯固态式激光雷达,采用激光时间飞行法,提供出色的三维图像成像和深度感知功能。特别适用于无人叉车领域,为叉尖避障提供卓越的三维成像和深度感知功能。它的高精度、自适应自动曝光、小尺寸、低功耗…...
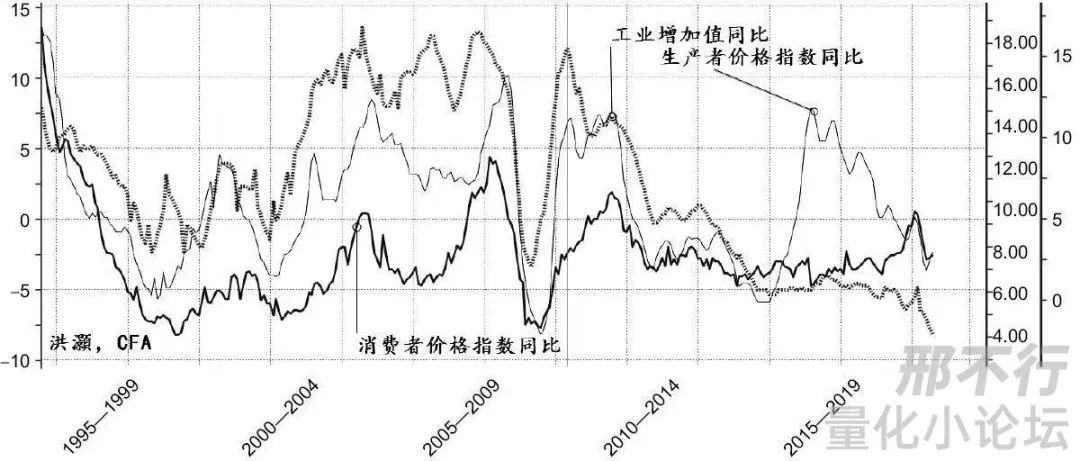
精华帖分享 | 低估值还能涨多久?
本文来源于量化小论坛策略分享会板块精华帖,作者为亮子,发布于2024年3月19日。 这两年,A股给我们的感觉就是成长股坍塌,高股息低估值的股票扛起大旗。表现出来就是中国神华、中海油这样的垄断型央国企大涨,包括移动联通…...

如何制作一个自己的网站?
在今天的互联网时代,网站展示已经是一个很基础的营销工具。不管是企业、还是个人,如何制作一个自己的网站?本文将会提供一个全面的基础制作网页教程,教你如何从零开始制作网页。 网页制作的基础知识:HTML、CSS和JavaS…...

torch报错
The Kernel crashed while executing code in the current cell or a previous cell. Please review the code in the cell(s) to identify a possible cause of the failure. Click here for more info. View Jupyter log for further details. 从日志中可以看出,内…...

深入探索卷积神经网络(CNN):图像分类的利器
深入探索卷积神经网络(CNN):图像分类的利器 前言CNN的崛起:为何我们需要它?图像卷积:CNN的基石轮廓过滤器:捕捉边缘特征 图像池化:降低维度的利器CNN的组成:卷积层、池化…...
网站建设中需要注意哪些安全问题?----雷池社区版
服务器与应用安全指南 1. 服务器安全 1.1 操作系统安全 及时更新补丁:确保操作系统始终安装最新补丁,以防范系统漏洞。例如,Windows Server 定期推送安全更新,修复如远程代码执行等潜在威胁。优化系统服务配置:关闭不…...

光控资本:养老金融建设提速 高速铜缆市场空间广阔
养老金融制作提速 金融监管总局办公厅近来印发的《关于大力展开商业保险年金有关事项的奉告》(下称《奉告》)提出,进一步扩大商业养老金业务试点;开发习惯个人养老金准则的新产品和专属产品;保险公司要坚持长期出资、…...

部署前后端分离若依项目--CentOS7宝塔版
准备: CentOS7服务器一台 通过网盘分享的文件:CentOS 7 h 链接: https://pan.baidu.com/s/17DF8eRSSDuj9VeqselGa_Q 提取码: s7x4 大家有需要可以下载这个,密码61 若依前端编译后文件 通过网盘分享的文件:ruoyi-admin.jar 链…...

ubuntu22.04 R Rstudio conda python 深大
一、配置IP network:version: 2renderer: networkdethernets:eth0:dhcp4: noaddresses:- 172.20.0.52/24gateway4: 172.20.0.2nameservers:addresses: [8.8.8.8, 8.8.4.4] 二、update apt update apt upgrade 三、安装python ubuntu 22.04安装python3 在Ubuntu 22.04上安装…...

二百七十一、Kettle——ClickHouse增量导入数据清洗记录表
一、目的 在完成错误数据表任务后,需要对每条错误数据的错误字段及其字段值进行分析 Hive中原有SQL语句和ClickHouse现有SQL语句很大不同 二、Hive中原有代码 2.1 表结构 --31、静态排队数据清洗记录表 create table if not exists hurys_db.dwd_data_clean_…...

为什么说Tcp是面向字节流的以及(Tcp粘包问题、TCP/UDP对比、listen函数的backlog参数的意义)
为什么说Tcp是面向字节流的: Tcp通信的本质是创建一个tcp的socket,同时就会对应的创建一个发送缓冲区和接收缓冲区。 调用write时, 数据会先写入发送缓冲区中;如果发送的字节数太长, 会被拆分成多个TCP的数据包发出如果发送的字节数太短, 就会先在缓冲…...

Flink PostgreSQL CDC源码解读:深入理解数据流同步
目录 一、PostgreSQL的数据捕获和复制机制 二、WAL日志格式 三、Debezium部署架构 3.1 Kafka Connect With Debezium 3.2 Debezium Server 编辑3.3 作为嵌入式引擎 四、Flink Postgres CDC源码解读 4.1. 如何捕捉数据和更新快照 4.2. 捕获的数据怎么从Postgres SQL…...

系统架构设计师 软件架构的定义与生命周期
软件架构的定义 通过一系列的设计活动,以满足系统的功能性需求和符合一定的非功能性需求与质量属性有相似含义的软件系统框架模式。在软件体系结构设计过程中,主要考虑的是系统的非功能性需求 软件体系结构设计经验的总结与重用是软件工程的重要目标之一…...

从零开始使用Surya-OCR最新版本0.6.1——最强文本检测模型:新添表单表格检测识别
目录 一、更新概述 二、环境安装 1.基础环境配置 2.模型参数下载 3.参数地址配置——settings.py 三、指令使用 1.命令指令运行 一、更新概述 surya项目Github地址:https://github.com/VikParuchuri/surya 号称今年最强OCR的surya近期迎来新的更新,Vik…...

linux中级wed服务器(https搭建加密服务器)
一。非对称加密算法: 公钥:公共密钥,开放 私钥:私有密钥,保密 1.发送方用自己的公钥加密,接受方用发送方的私钥解密:不可行 2.发送方用接受方的公钥加密,接受方用自己的私钥解密…...

聊一聊为什么企业数字化转型总是三天热度
听到“数字化转型”,是不是脑子里立马蹦出各种炫酷词汇:AI、大数据、物联网、区块链……瞬间觉得公司马上就要起飞?可惜,现实往往是:转型刚刚起步时大家热血沸腾,结果没过多久一哄而散。最终,这…...

2025年NPDP产品经理认证考试时间和报考条件
在报考2025年NPDP认证考试前,了解NPDP相关考试信息是非常重要的,可以帮助我们更好地制定备考计划,提高学习效率。 NPDP考试时间 NPDP考试每年举办两次,分别在5月和11月进行,且考试一般安排在周末,以便在职的专业人士…...

微信小程序文字转语音播报案例
插件申请 在小程序官方申请同声传译插件,地址: mp.weixin.qq.com 引入插件 在app.json中加入 "plugins": {"WechatSI": {"version": "0.3.6","provider": "wx069ba97219f66d99"}},封装…...

QT SSDP 局域网检测支持扫描通信
一. 什么是SSDP? 简单服务发现协议(SSDP,Simple Service Discovery Protocol)是一种应用层协议,简单服务发现协议是在HTTPU和HTTPMU的基础上实现的协议。简单服务发现协议(SSDP)提供了在局域网里面发现设备的机制。客户端可以通过使用SSDP,根据自己的需要,在局域网查找特…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
