无用的知识又增加了-静态二值贝叶斯滤波
静态二值贝叶斯滤波
静态二值贝叶斯滤波(Static Binary Bayes Filter)是一种用于处理二值状态(例如,目标存在或不存在)的简单贝叶斯滤波器。这种滤波器通常应用于目标检测、传感器融合等场景,其中状态空间是离散且只有两个可能的状态。
基本概念
- 状态:二值状态 ( x x x ) 可以是 0 或 1,表示目标不存在或存在。
- 观测:观测 ( z z z ) 也可以是 0 或 1,表示没有检测到目标或检测到目标。
- 先验概率:目标存在的先验概率 ( P ( x = 1 ) P(x = 1) P(x=1) ) 和目标不存在的先验概率 ( P ( x = 0 ) P(x = 0) P(x=0) )。
- 似然概率:在给定状态 ( x x x) 的情况下,观测 ( z z z ) 的概率 ( P ( z ∣ x ) P(z | x) P(z∣x) )。
- 后验概率:在给定观测 ( z z z ) 的情况下,状态 ( x x x ) 的概率 ( P ( x ∣ z ) P(x | z) P(x∣z) )。
数学描述
假设我们有一个二值状态 ( x ∈ { 0 , 1 } x \in \{0, 1\} x∈{0,1} ),以及一个二值观测 ( z ∈ { 0 , 1 } z \in \{0, 1\} z∈{0,1} )。
1. 先验概率
定义目标存在的先验概率 ( P ( x = 1 ) P(x = 1) P(x=1) ) 和目标不存在的先验概率 ( P ( x = 0 ) P(x = 0) P(x=0) ):
P ( x = 1 ) = p 1 P ( x = 0 ) = p 0 = 1 − p 1 P(x = 1) = p_1\\ P(x = 0) = p_0 = 1 - p_1 P(x=1)=p1P(x=0)=p0=1−p1
2. 似然概率
定义在给定状态 ( x x x ) 的情况下,观测 ( z ) 的概率 ( P ( z ∣ x ) P(z | x) P(z∣x) ):
P ( z = 1 ∣ x = 1 ) = p 11 P ( z = 0 ∣ x = 1 ) = p 10 = 1 − p 11 P ( z = 1 ∣ x = 0 ) = p 01 P ( z = 0 ∣ x = 0 ) = p 00 = 1 − p 01 P(z = 1 | x = 1) = p_{11} \\ P(z = 0 | x = 1) = p_{10} = 1 - p_{11} \\ P(z = 1 | x = 0) = p_{01} \\ P(z = 0 | x = 0) = p_{00} = 1 - p_{01} P(z=1∣x=1)=p11P(z=0∣x=1)=p10=1−p11P(z=1∣x=0)=p01P(z=0∣x=0)=p00=1−p01
3. 后验概率
根据贝叶斯定理,计算在给定观测 ( z z z ) 的情况下,状态 ( x x x ) 的后验概率 ( P ( x ∣ z ) P(x | z) P(x∣z) ):
P ( x = 1 ∣ z ) = P ( z ∣ x = 1 ) ⋅ P ( x = 1 ) P ( z ) P ( x = 0 ∣ z ) = P ( z ∣ x = 0 ) ⋅ P ( x = 0 ) P ( z ) P(x = 1 | z) = \frac{P(z | x = 1) \cdot P(x = 1)}{P(z)} \\ P(x = 0 | z) = \frac{P(z | x = 0) \cdot P(x = 0)}{P(z)} P(x=1∣z)=P(z)P(z∣x=1)⋅P(x=1)P(x=0∣z)=P(z)P(z∣x=0)⋅P(x=0)
其中,( $P(z) $) 是归一化常数,可以通过全概率公式计算:
P ( z ) = P ( z ∣ x = 1 ) ⋅ P ( x = 1 ) + P ( z ∣ x = 0 ) ⋅ P ( x = 0 ) P(z) = P(z | x = 1) \cdot P(x = 1) + P(z | x = 0) \cdot P(x = 0) P(z)=P(z∣x=1)⋅P(x=1)+P(z∣x=0)⋅P(x=0)
示例代码
下面是一个简单的 C 语言实现示例,展示如何使用静态二值贝叶斯滤波进行状态估计。假设我们有一个简单的系统,状态和观测都是二值的。
#include <stdio.h>// 定义状态和观测的概率
double prior_prob_x1 = 0.5; // 目标存在的先验概率 P(x = 1)
double prior_prob_x0 = 0.5;
double likelihood_z1_given_x1 = 0.7; // P(z = 1 | x = 1)
double likelihood_z0_given_x1 = 0.3; // P(z = 0 | x = 1)
double likelihood_z1_given_x0 = 0.1; // P(z = 1 | x = 0)
double likelihood_z0_given_x0 = 0.9; // P(z = 0 | x = 0)// 计算归一化常数 P(z)
double calculate_normalization_constant(int z) {if (z == 1) {return (likelihood_z1_given_x1 * prior_prob_x1) + (likelihood_z1_given_x0 * (1 - prior_prob_x1));}else {return (likelihood_z0_given_x1 * prior_prob_x1) + (likelihood_z0_given_x0 * (1 - prior_prob_x1));}
}double _calculate_normalization_constant_(int z) {if (z == 1) {return (likelihood_z1_given_x0 * prior_prob_x0) + (likelihood_z1_given_x1 * (1 - prior_prob_x0));}else {return (likelihood_z0_given_x0 * prior_prob_x0) + (likelihood_z0_given_x1 * (1 - prior_prob_x0));}
}// 计算后验概率 P(x | z)
void update_belief(int z, double* posterior_prob_x1) {double normalization_constant = calculate_normalization_constant(z);if (z == 1) {*posterior_prob_x1 = (likelihood_z1_given_x1 * prior_prob_x1) / normalization_constant;}else {*posterior_prob_x1 = (likelihood_z0_given_x1 * prior_prob_x1) / normalization_constant;}
}void _update_belief_(int z, double* posterior_prob_x0) {double normalization_constant = _calculate_normalization_constant_(z);if (z == 1) {*posterior_prob_x0 = (likelihood_z1_given_x0 * prior_prob_x0) / normalization_constant;}else {*posterior_prob_x0 = (likelihood_z0_given_x0 * prior_prob_x0) / normalization_constant;}
}int main() {double posterior_prob_x1;double posterior_prob_x0;// 初始先验概率printf("Initial Prior Probability: P(x = 1) = %.4f\n", prior_prob_x1);printf("Initial Prior Probability: P(x = 0) = %.4f\n", prior_prob_x0);// 第一次观测int observation = 1; // 假设观测到的是 1printf("Observation: %d\n", observation);update_belief(observation, &posterior_prob_x1);printf("Posterior Probability after Observation: P(x = 1 | z = %d) = %.4f\n", observation, posterior_prob_x1);_update_belief_(observation, &posterior_prob_x0);printf("Posterior Probability after Observation: P(x = 0 | z = %d) = %.4f\n", observation, posterior_prob_x0);// 更新先验概率为上一次的后验概率prior_prob_x1 = posterior_prob_x1;prior_prob_x0 = posterior_prob_x0;// 第二次观测observation = 0; // 假设观测到的是 0printf("Observation: %d\n", observation);update_belief(observation, &posterior_prob_x1);printf("Posterior Probability after Observation: P(x = 1 | z = %d) = %.4f\n", observation, posterior_prob_x1);_update_belief_(observation, &posterior_prob_x0);printf("Posterior Probability after Observation: P(x = 0 | z = %d) = %.4f\n", observation, posterior_prob_x0);// 更新先验概率为上一次的后验概率prior_prob_x1 = posterior_prob_x1;prior_prob_x0 = posterior_prob_x0;// 第三次观测observation = 0; // 假设观测到的是 0printf("Observation: %d\n", observation);update_belief(observation, &posterior_prob_x1);printf("Posterior Probability after Observation: P(x = 1 | z = %d) = %.4f\n", observation, posterior_prob_x1);_update_belief_(observation, &posterior_prob_x0);printf("Posterior Probability after Observation: P(x = 0 | z = %d) = %.4f\n", observation, posterior_prob_x0);return 0;
}
详细步骤解释
-
定义概率:
- 定义目标存在的先验概率
prior_prob_x1。 - 定义似然概率
likelihood_z1_given_x1、likelihood_z0_given_x1、likelihood_z1_given_x0和likelihood_z0_given_x0。
- 定义目标存在的先验概率
-
计算归一化常数:
calculate_normalization_constant函数根据观测 ( z z z ) 计算归一化常数 ( P ( z ) P(z) P(z) )。
-
更新后验概率:
update_belief函数根据贝叶斯定理计算后验概率 ( $P(x | z) $)。- 根据观测 ( z z z ) 更新后验概率
posterior_prob_x1。
-
打印结果:
- 打印初始先验概率。
- 进行多次观测,并打印每次观测后的后验概率。
通过这些步骤,你可以实现一个简单的静态二值贝叶斯滤波器,并根据观测数据不断更新状态估计。这个示例展示了基本的原理,实际应用中可能需要更复杂的模型和更多的优化。
相关文章:

无用的知识又增加了-静态二值贝叶斯滤波
静态二值贝叶斯滤波 静态二值贝叶斯滤波(Static Binary Bayes Filter)是一种用于处理二值状态(例如,目标存在或不存在)的简单贝叶斯滤波器。这种滤波器通常应用于目标检测、传感器融合等场景,其中状态空间…...
控制)
cesium相机(camera)控制
camera基础属性: Cesium 中的相机通过 viewer.camera 来获取和操作。 position:相机的位置,用 Cartesian3 坐标表示,表示的是相机在世界坐标系中的绝对位置。 viewer.camera.position Cesium.Cartesian3.fromDegrees(longitude, latitude, height);dir…...

Java 反射
一、基本概念 Java反射机制是Java语言的一种动态特性,允许程序在运行时检查和操作类、接口、字段和方法。反射机制使得Java程序可以在运行时获取关于类的详细信息,并且可以动态地调用类的方法、访问类的字段等。反射机制主要涉及以下几个核心类和接口&a…...

【目标检测01】真实框、预测框、锚框和交并比IoU
文章目录 1. 任务定义2. 基本概念2.1 边界框(bounding box)2.2 真实框、预测框和锚框2.3 交并比 (IoU)2.4 代码实现 1. 任务定义 目标检测的主要目的是让计算机可以自动识别图片或者视频帧中所有目标的类别,并在该目标周围绘制边界框&#x…...
)
青少年编程能力等级测评CPA C++五级试卷(2)
青少年编程能力等级测评CPA C++五级试卷(2) 一、单项选择题(共15题,每题3分,共45分) CP5_2_1.下列有关类的重用方法的叙述中,不正确的是( )。 A.类的继承可以实现类的重用 B.类的组合可以实现类的重用 C.类的封装可以实现类的重用 D.类的继承和类的组合都可…...

SATA数据线
SATA 数据线(Serial ATA 数据线)是一种用于连接计算机主板与存储设备(如硬盘、固态硬盘和光驱)的线缆。它的主要作用是传输数据,允许计算机与这些设备之间进行高效的数据交换。 主要作用 数据传输:SATA 数…...

《云原生安全攻防》-- K8s攻击案例:权限维持的攻击手法
在本节课程中,我们将一起深入了解K8s权限维持的攻击手法,通过研究这些攻击手法的技术细节,来更好地认识K8s权限维持所带来的安全风险。 在这个课程中,我们将学习以下内容: K8s权限维持:简单介绍K8s权限维持…...

回溯算法-Java【力扣】【算法学习day.14】
前言 ###我做这类文档一个重要的目的还是给正在学习的大家提供方向(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非常非常高滴&am…...

从本地到云端:跨用户请求问题的完美解决方案
对于某些单个请求或响应中含有多个用户信息的服务,SDK提供了一套基于统一的UCS拆分和聚合的解决方案供开发者使用。 请求拆分 对于跨用户服务的请求,我们提供了两个处理方案: 【1】根据用户信息拆分请求: 场景:请求内…...

leetcode day4 409+5
409 最长回文串 给定一个包含大写字母和小写字母的字符串 s ,返回 通过这些字母构造成的 最长的 回文串 的长度。 在构造过程中,请注意 区分大小写 。比如 "Aa" 不能当做一个回文字符串。 示例 1: 输入:s "abccccdd" 输出:7 解…...

英语语法学习框架(考研)
一、简单句 英语都是由简单句构成,简单句共有五种基本句型:①主谓;②主谓宾;③主谓宾宾补;④主谓宾间宾(间接宾语);⑤主系表; 其中谓语是句子最重要的部分,谓…...

基于neo4j的学术论文关系管理系统
正在为毕业设计头疼?又或者在学术研究中总是找不到像样的工具来管理浩瀚的文献资料?今天给大家介绍一款超实用的工具——基于Neo4j的学术论文关系管理系统,让你轻松搞定学术文献的管理与展示!🎉 系统的核心是什么呢&a…...

C#中的委托、匿名方法、Lambda、Action和Func
委托 委托概述 委托是存有对某个方法的引用的一种引用类型变量。定义方法的类型,可以把一个方法当作另一方法的参数。所有的委托(Delegate)都派生自 System.Delegate 类。委托声明决定了可由该委托引用的方法。 # 声明委托类型 委托类型声…...

IDEA关联Tomcat——最新版本IDEA 2024
1.链接Tomcat到IDEA上 添加Tomcat到IDEA上有两种方式: 第一种: (1)首先,来到欢迎界面,找到左侧的Customize选项 (2)然后找到Build、Execution、Deployment选项 (3&am…...

【如何获取股票数据18】Python、Java等多种主流语言实例演示获取股票行情api接口之沪深A股解禁限售数据获取实例演示及接口API说明文档
最近一两年内,股票量化分析逐渐成为热门话题。而从事这一领域工作的第一步,就是获取全面且准确的股票数据。因为无论是实时交易数据、历史交易记录、财务数据还是基本面信息,这些数据都是我们进行量化分析时不可或缺的宝贵资源。我们的主要任…...

NVR小程序接入平台/设备EasyNVR多品牌NVR管理工具/设备的多维拓展与灵活应用
在数字化安防时代,NVR批量管理软件/平台EasyNVR作为一种先进的视频监控系统设备,正逐步成为各个领域监控解决方案的首选。NVR批量管理软件/平台EasyNVR作为一款基于端-边-云一体化架构的国标视频融合云平台,凭借其部署简单轻量、功能多样、兼…...
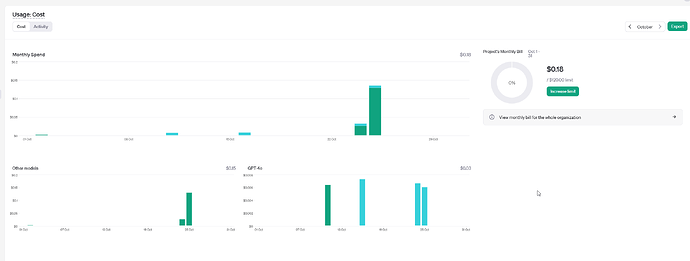
GPT-4o 和 GPT-4 Turbo 模型之间的对比
GPT-4o 和 GPT-4 Turbo 之间的对比 备注 要弄 AI ,不同模型之间的对比就比较重要。 GPT-4o 是 GPT-4 Turbo 的升级版本,能够提供比 GPT-4 Turbo 更多的内容和信息,但成功相对来说更高一些。 第三方引用 在 2024 年 5 月 13 日࿰…...

gin入门教程(10):实现jwt认证
使用 github.com/golang-jwt/jwt 实现 JWT(JSON Web Token)可以有效地进行用户身份验证,这个功能往往在接口前后端分离的应用中经常用到。以下是一个基本的示例,演示如何在 Gin 框架中实现 JWT 认证。 目录结构 /hello-gin │ ├── cmd/ …...

Python 基础语法 - 数据类型
顾名思义,计算机就是用来做数学计算的机器,因此,计算机程序理所当然的可以处理各种数值。但是,计算机能处理的远远不止数值,还可以处理文本,图形,音频,视频,网页等各种各…...
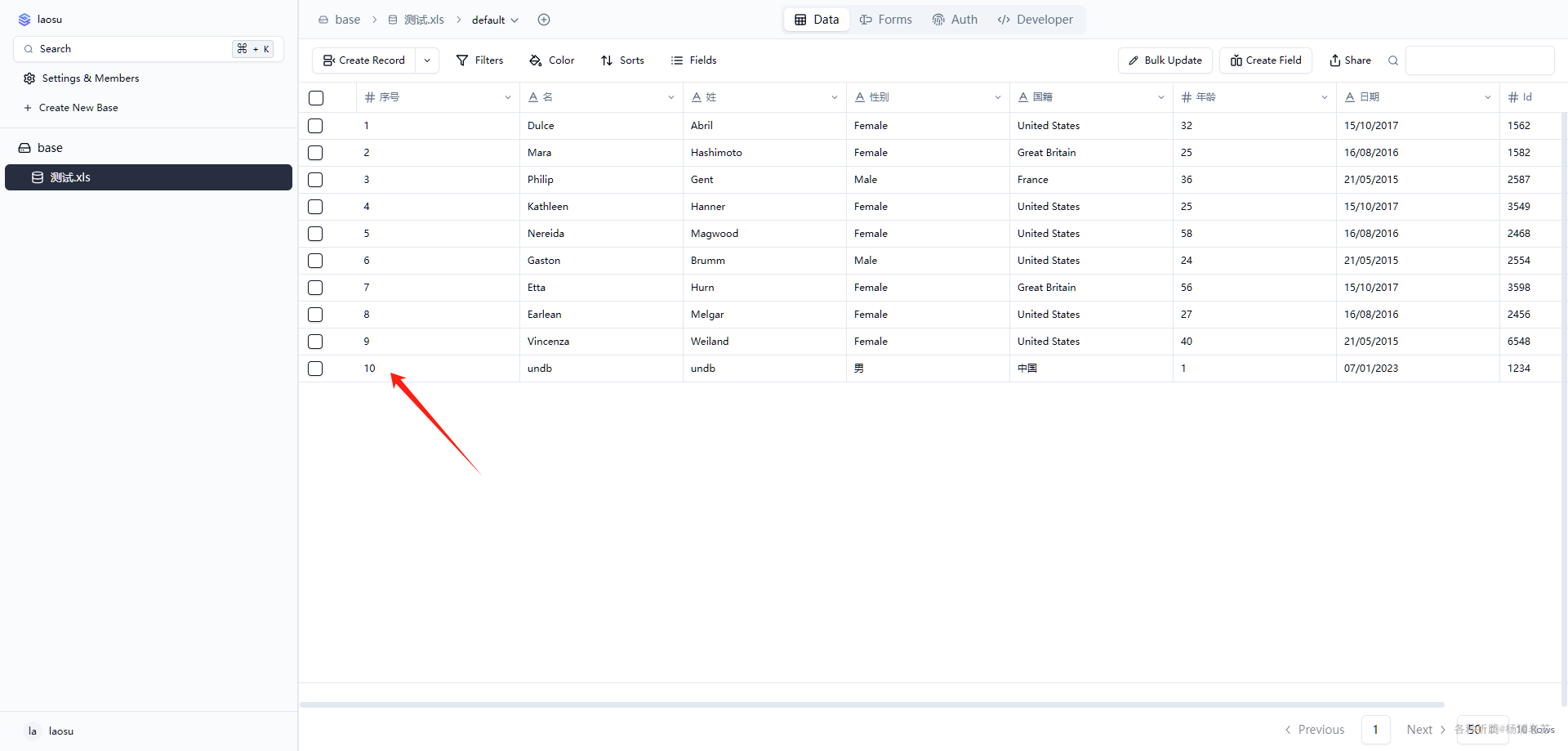
自托管无代码数据库Undb
什么是 Undb ? Undb 是一个无代码平台,也可以作为后端即服务 (BaaS)。它基于 SQLite,可以使用 Bun 打包成二进制文件用于后端服务。此外,它可以通过 Docker 部署为服务,提供表管理的 UI。 软件特点: ⚡ 无…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
