当前位置： 首页 > news >正文

通过FDM升级Firepower

news 2026/2/8 14:25:41

1.基本说明

本文主要主要介绍如何通过FDM来升级Firepower设备，这里以FPR1010设备为例，那么什么事Firepower、FDM呢？在开始之前，进行简单的介绍。

Firepower：思科 Firepower 是网络安全和流量管理产品的集成套件，可以部署在专用平台上或作为软件解决方案部署。

FDM：Firepower Device Management，熟悉Cisco防火墙的朋友可能听过FMC，FDM，简而言之，FDM是设备中的本地管理选项，而 fmc 是单独的管理工具。两者都可以用来管理FTD设备。

其他术语：

  • FTD（Firepower Threat Defense）：思科 Firepower 威胁防御是一种集成软件镜像，将 CISCO ASA 和 Firepower 功能结合到一个硬件和软件包容性系统中。
  • FMC (Firepower Management Centre)：FMC 管理 2100、3100、4100 和 9300 硬件。在硬件之上运行 FTD（或 ASA）软件镜像。

2.升级准备

当前软件版本：Release 6.4.0-102

目标软件版本：Release 6.5.0-115

3.升级操作

如下是Firepower主页页面。

3.1.镜像获取

在思科官网获取升级的目标镜像版本。

3.2.进入Updates界面

在如下页面选择Updates进入。

3.3.选择升级文件

在System update这里点击browse，选择我们下载好的镜像。

等待镜像上传。

3.4.进行Install

可以看到Install是需要reload重启的，这个时候我们可以选择点击Install，并进一步点击continue。

3.5.确认升级情况

设备重启后需要重新登录一下FDM。

进入之后可以看到目前的版本已经升级成功为目标版本。

如果有需要部署的内容，可以进入Updates界面，然后进行Deployment...

好啦~本次记录就到这里了！

相关文章：

通过FDM升级Firepower

1.基本说明 本文主要主要介绍如何通过FDM来升级Firepower设备，这里以FPR1010设备为例，那么什么事Firepower、FDM呢？在开始之前，进行简单的介绍。 Firepower：思科 Firepower 是网络安全和流量管理产品的集成套件&…...

编程日记 2024/10/27 0:20:27

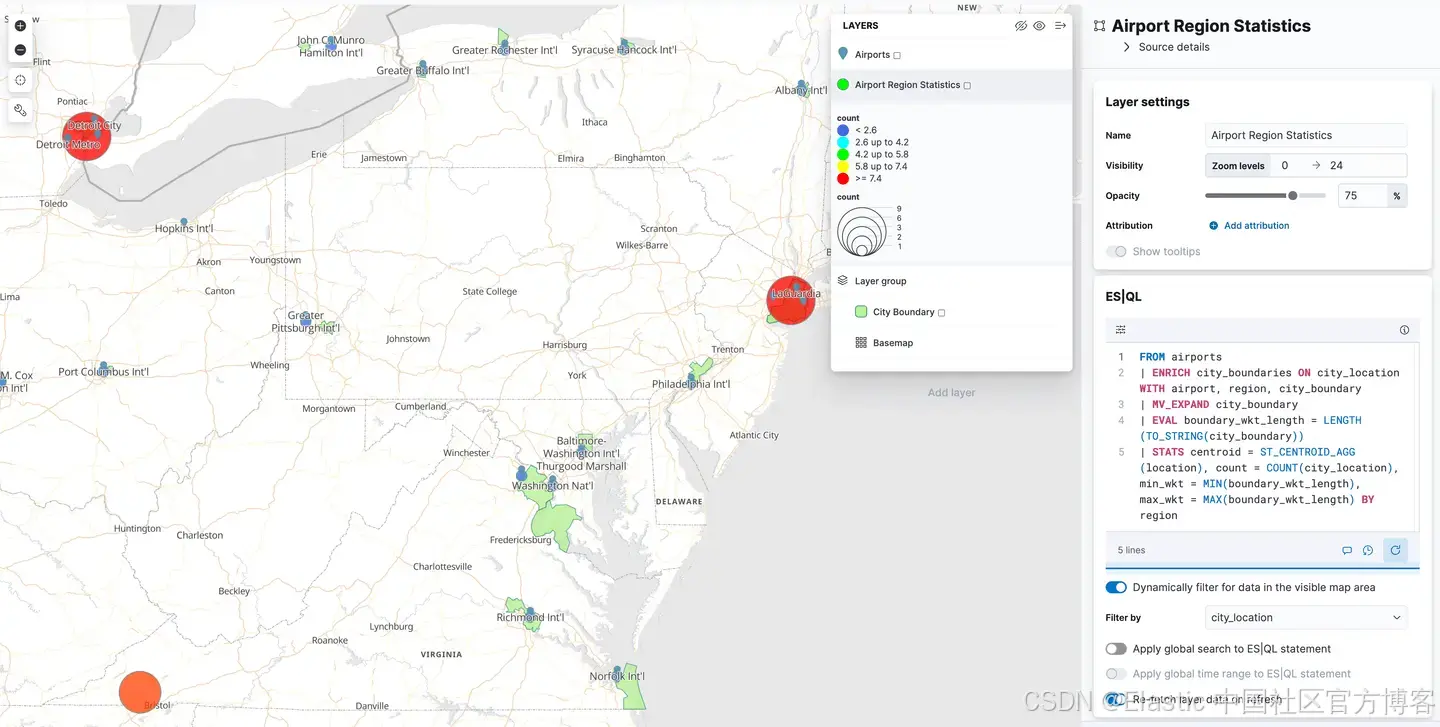
使用 Kibana 将地理空间数据导入 Elasticsearch 以供 ES|QL 使用

作者：来自 Elastic Craig Taverner 如何使用 Kibana 和 csv 采集处理器将地理空间数据采集到 Elasticsearch 中，以便在 Elasticsearch 查询语言 (ES|QL) 中进行搜索。Elasticsearch 具有强大的地理空间搜索功能，现在 ES|QL 也具备这些功能&am…...

编程日记 2024/10/27 0:17:24

demo说明

代码说明 MDIO总线的注册和初始化：分配并注册MDIO总线，用于与PHY设备通信。 网络设备的创建：分配网络设备（如以太网接口）。 PHY设备连接：通过phy_connect函数连接PHY设备，指定回调函数my_adj…...

编程日记 2024/10/27 0:16:24

【c++篇】：从基础到实践--c++内存管理技巧与模版编程基础

✨感谢您阅读本篇文章，文章内容是个人学习笔记的整理，如果哪里有误的话还请您指正噢✨ ✨个人主页：余辉zmh–CSDN博客 ✨ 文章所属专栏：c篇–CSDN博客 文章目录 前言一.c/c内存分布二.c/c的动态内存管理方式2.1.c语言的动态内存管…...

编程日记 2024/10/27 0:14:22

如何减小 Maven 项目生成的 JAR 包体积 提升运维效率

在使用 Maven 构建 Java 项目时，有时需要减小生成的 JAR 包的体积，以提高部署效率或减少资源消耗。以下是一些有效的方法来减小 JAR 包的体积： 排除不必要的依赖打包时，依赖jar包独立于应用jar包 1. 排除不必要的依赖 通过排除项目…...

编程日记 2024/10/27 0:13:21

Python自动化会议记录与摘要生成

前言 在现代工作环境中，会议是团队沟通和决策的重要方式。然而，整理会议记录和生成摘要往往是一项耗时且容易出错的任务。幸运的是，借助Python编程语言以及一些强大的库，我们可以自动化这一过程，让机器帮助我们完成这…...

编程日记 2024/10/27 0:09:16

SwiftUI 中 List 或 Form 子视图关联的 swipeAction 导致展开动画异常的解决

问题现象 小伙伴们都知道，在 SwiftUI 中更快捷的增强 List 或 Form 子视图（Cell）交互功能的方法是使用 swipeAction 修改器。不过，对其使用稍有不慎也会横生枝节。 如上图所示，不适当的设置 Cell 视图布局会使 swipeAction 无法生成正确的收缩和展开动画。对此我们有什么…...

编程日记 2024/10/27 0:08:16

Apache Paimon Catalog

Paimon Catalog可以持久化元数据，当前支持两种类型的metastore： 文件系统（默认）：将元数据和表文件存储在文件系统中。hive：在 hive metastore中存储元数据。用户可以直接从 Hive 访问表。 2.2.1 文件系统…...

编程日记 2024/10/27 0:06:13

C++基础：三个字符串也能搞大小？

上一篇说了三个整数比较大小，按照顺序输入的，这次我们看看字符串的，顺便把那个简化以下： 题目:这次输入三个字符串。如果用户输入“Stenbeck", “Hemingway”,“Fitzgerald”,输出将是“Fitzgerald，Hemingway&…...

编程日记 2024/10/27 0:04:10

了解AIGC——自然语言处理与生成

AIGC——自然语言处理与生成：揭秘AI如何生成语言 近年来，AIGC（AI Generated Content）技术迅猛发展，自然语言处理（Natural Language Processing, NLP）与生成技术的结合，使得机器不仅…...

编程日记 2024/10/27 0:03:09

Modern CMake 简明教程（8）- 集成Qt

在项目中集成 Qt 库需要先使用 find_package 查找 Qt 的安装位置。对于 Qt4， CMake 使用 Module 模式进行查找（FindQt4.cmake 由 CMake 提供），而 对于 Qt5、Qt6，则是使用 Config 模式进行查找，相应的 config 文件位于类似下面的目录中 D:\Qt\5.15.2\msvc2019\lib\cmake。…...

编程日记 2024/10/27 0:01:06

人脸应用实例：性别年龄预测

在当今科技飞速发展的时代，人脸识别技术已经从科幻电影走进了我们的日常生活。通过算法来识别人脸的特征，进而判断身份、年龄和性别，这一技术正逐步改变着我们的生活方式。今天，我们就来探讨一下基于深度学习的人脸应用实例——性…...

编程日记 2024/10/26 23:58:03

学习threejs，通过THREE.Raycaster给模型绑定点击事件

👨‍⚕️ 主页： gis分享者 👨‍⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨‍⚕️ 收录于专栏：threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.Raycaster光线投射概…...

编程日记 2024/10/26 23:57:02

Jackson Json序列化反序列化的两个坑

Jackson is a suite of data-processing tools for Java (and the JVM platform) Jackson最常用的Json序列化功能&#xff0c;引入如下的包即可&#xff1a; <properties>...<!-- Use the latest version whenever possible. --><jackson.version>2.17.1<…...

编程日记 2024/10/26 23:53:59

k8s_Pod健康检查

Kubernetes 3种探针介绍 LivenessProbe&#xff08;存活探针&#xff09; LivenessProbe 用于检查容器是否仍然活着。如果探针检测到容器已经失去响应&#xff0c;Kubernetes 将重启该容器。这通常用来修复由于内部状态错误或死锁引起的程序失效问题。 作用&#xff1a;检测容器…...

编程日记 2024/10/26 23:52:58

基于DDPG算法的股票量化交易

项目源码获取方式见文章末尾&#xff01; 回复暗号&#xff1a;13&#xff0c;免费获取600多个深度学习项目资料&#xff0c;快来加入社群一起学习吧。 **《------往期经典推荐------》**项目名称 1.【基于PyQTFaceNet卷积神经网络实现的学生人脸识别考勤系统】 2.【卫星图像道…...

编程日记 2024/10/26 23:51:57

eIQ笔记（UI介绍+Loss曲线+OpenART例程）

This is a very beginner-friendly article ^o^ 目录 🍂一、训练器设置 input size： learning rate： learning rate decay： Epochs: Decay Rate: Linear Decay: Batch Size： Epochs to Train： QAT（Quantization Aware Training）量化感知训练： Pruning剪枝…...

编程日记 2024/10/26 23:49:55

微信小程序——消息订阅

首先用到的就是wx.requestSubscribeMessage接口。 注意&#xff1a;用户发生点击行为或者发起支付回调后&#xff0c;才可以调起订阅消息界面 requestSubscribeMessage() {uni.requestSubscribeMessage({tmplIds: [],//需要订阅的消息模板的id的集合&#xff0c;一次调用最多可…...

编程日记 2024/10/26 23:45:51

网络原理（传输层）-＞TCP协议解

前言 大家好&#xff01;我是小帅&#xff0c;今天我们来学习TCP协议&#xff0c;个人主页 文章目录 1. TCP协议2. TCP的核心机制2.1TCP核心机制一&#xff1a;确认应答2.2 TCP核心机制二&#xff1a;超时重传2.3 TCP核心机制三&#xff1a;连接管理2.4 TCP核心机制四&#xf…...

编程日记 2024/10/26 23:43:50

oracle imp和exp 导入不同库的用户和表空间

参考&#xff1a; oracle 导入(imp)数据时的表空间(tablespace users)问题_imp tablespace-CSDN博客 网上的解决办法大概都是这种&#xff0c;但是实际测试19c数据库并不能成功&#xff0c;所以最后采取在导出文件上强行修改表空间的办法&#xff0c;改完后再继续执行导出导入…...

编程日记 2024/10/26 23:42:49

7.4.分块查找

一.分块查找的算法思想&#xff1a; 1.实例&#xff1a; 以上述图片的顺序表为例&#xff0c; 该顺序表的数据元素从整体来看是乱序的&#xff0c;但如果把这些数据元素分成一块一块的小区间&#xff0c; 第一个区间[0,1]索引上的数据元素都是小于等于10的&#xff0c; 第二…...

编程新知 2026/1/27 18:11:42

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2026/2/7 10:59:19

linux 错误码总结

1，错误码的概念与作用 在Linux系统中，错误码是系统调用或库函数在执行失败时返回的特定数值，用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递，errno由操作系统维护，保存最近一次发生的错误信息。值得注意的是，errno的值在每次系统调用或函数调用失败时…...

编程新知 2025/9/16 22:48:47

汇编常见指令

汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX&#xff08;不访问内存&#xff09;XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

编程新知 2026/1/23 2:04:44

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/12/2 3:35:50

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2026/2/4 16:21:14

Web中间件--tomcat学习

Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机&#xff0c;它可以执行Java字节码。Java虚拟机是Java平台的一部分&#xff0c;Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

编程新知 2025/9/13 18:20:34

「全栈技术解析」推客小程序系统开发：从架构设计到裂变增长的完整解决方案

在移动互联网营销竞争白热化的当下&#xff0c;推客小程序系统凭借其裂变传播、精准营销等特性&#xff0c;成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径&#xff0c;助力开发者打造具有市场竞争力的营销工具。​ 一、系统核心功能架构&…...

编程新知 2025/8/21 16:28:18

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter

java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用&#xff08;Math::max&#xff09; 2 函数接口…...

编程新知 2026/2/4 6:10:10

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50