【动手学强化学习】part2-动态规划算法
阐述、总结【动手学强化学习】章节内容的学习情况,复现并理解代码。
文章目录
- 一、什么是动态规划?
- 1.1概念
- 1.2适用条件
- 二、算法示例
- 2.1问题建模
- 2.2策略迭代(policyiteration)算法
- 2.2.1伪代码
- 2.2.2完整代码
- 2.2.3运行结果
- 2.2.4代码流程概述
- 2.3价值迭代(value iteration)算法
- 2.3.1伪代码
- 2.3.2完整代码
- 2.3.3运行结果
- 2.4截断策略迭代(Truncated policy iteration)
- 2.4.1伪代码
- 小结
一、什么是动态规划?
1.1概念
**动态规划(dynamic programming)**是程序设计算法中非常重要的内容,能够高效解决一些经典问题,例如背包问题和最短路径规划。动态规划的基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到目标问题的解。动态规划会保存已解决的子问题的答案,在求解目标问题的过程中,需要这些子问题答案时就可以直接利用,避免重复计算。
基于动态规划的强化学习算法主要有两种:一是策略迭代(policy iteration),二是价值迭代(value iteration)。
1.2适用条件
需要“白盒”环境(model-based)!!!基于动态规划的这两种强化学习算法要求事先知道环境的状态转移函数和奖励函数,也就是需要知道整个马尔可夫决策过程。策略迭代和价值迭代通常只适用于有限马尔可夫决策过程,即状态空间和动作空间是离散且有限的。
二、算法示例
2.1问题建模
CliffWalking悬崖漫步环境
- 目标:要求一个智能体从起点出发,避开悬崖行走,最终到达目标位置。

根据MDP过程进行建模:
- 状态空间:4×12 的网格世界,每一个网格表示一个状态。起点是左下角的状态,目标是右下角的状态。
- 动作空间:可以采取 4 种动作:上、下、左、右。
- 折扣因子:取0.9。
- 奖励函数:智能体采取动作后触碰到边界墙壁则状态不发生改变,否则就会相应到达下一个状态。环境中有一段悬崖,智能体掉入悬崖或
到达目标状态都会结束动作并回到起点,也就是说掉入悬崖或者达到目标状态是终止状态。智能体每走一步的奖励是 −1,掉入悬崖的奖励是−100。 - 状态转移函数:
2.2策略迭代(policyiteration)算法
2.2.1伪代码

- 算法流程简述:
①初始化:根据环境,初始化各state的state value,一般设置为0;policy同时也初始化,一般设置为每个state选取各action的概率相等
②价值评估(policy evaluation,PE):循环迭代计算,毕竟当前policy下稳态state value
③策略提升(policy improvement):依据当前statevalue值,根据环境模型( p ( r ∣ s , a ) p(r|s,a) p(r∣s,a)、 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a))计算各(s,a)对action value,并以greedy policy策略将各state中action value最大的值进行policy优化
④终止判断:判断最近两次policy是否相等,若是则停止算法输出policy,若否则重复执行②③步。
2.2.2完整代码
# =============================================================================
#
# 悬崖漫步是一个非常经典的强化学习环境,它要求一个智能体从起点出发,避开悬崖行走,最终到达目标位置。
# state:如图 4-1 所示,有一个 4×12 的网格世界,每一个网格表示一个状态,智能体的起点是左下角的状态,目标是右下角的状态.
# action:智能体在每一个状态都可以采取 4 种动作:上、下、左、右。
# goal:如果智能体采取动作后触碰到边界墙壁则状态不发生改变,否则就会相应到达下一个状态。环境中有一段悬崖,智能体掉入悬崖或
# 到达目标状态都会结束动作并回到起点,也就是说掉入悬崖或者达到目标状态是终止状态。
# reward:智能体每走一步的奖励是 −1,掉入悬崖的奖励是−100。
# =============================================================================import copyclass CliffWalkingEnv:""" 悬崖漫步环境"""def __init__(self, ncol=12, nrow=4):self.ncol = ncol # 定义网格世界的列self.nrow = nrow # 定义网格世界的行# 转移矩阵P[state][action] = [(p, next_state, reward, done)]包含下一个状态和奖励self.P = self.createP()def createP(self):# =============================================================================
# 转移矩阵P[s][a] = [(p, next_state, reward, done)]包含下一个状态和奖励
# p:s到next_state的状态转移概率,在这里都取1
# reward:s到next_state的即时奖励
# done:是否到达终点或悬崖
# =============================================================================# 初始化P = [[[] for j in range(4)] for i in range(self.nrow * self.ncol)]# 4种动作, change[0]:上,change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)# 定义在左上角change = [[0, -1], [0, 1], [-1, 0], [1, 0]]for i in range(self.nrow):for j in range(self.ncol):for a in range(4):# 位置在悬崖或者目标状态,因为无法继续交互,任何动作奖励都为0if i == self.nrow - 1 and j > 0:# 除了4行1列的元素的done状态都设置为True,其都为悬崖,除4行12列为终点P[i * self.ncol + j][a] = [(1, i * self.ncol + j, 0,True)]continue# 其他位置next_x = min(self.ncol - 1, max(0, j + change[a][0]))next_y = min(self.nrow - 1, max(0, i + change[a][1]))next_state = next_y * self.ncol + next_xreward = -1done = False# 下一个位置在悬崖或者终点if next_y == self.nrow - 1 and next_x > 0:done = Trueif next_x != self.ncol - 1: # 下一个位置在悬崖reward = -100P[i * self.ncol + j][a] = [(1, next_state, reward, done)]return Pclass PolicyIteration:""" 策略迭代算法 """def __init__(self, env, theta, gamma):self.env = envself.v = [0] * self.env.ncol * self.env.nrow # 初始化价值为0#🌟初始策略是均匀分布的self.pi = [[0.25, 0.25, 0.25, 0.25]for i in range(self.env.ncol * self.env.nrow)] # 初始化为均匀随机策略self.theta = theta # 策略评估收敛阈值self.gamma = gamma # 折扣因子def policy_evaluation(self): # 策略评估cnt = 1 # 计数器while 1:max_diff = 0new_v = [0] * self.env.ncol * self.env.nrowfor s in range(self.env.ncol * self.env.nrow):qsa_list = [] # 开始计算状态s下的所有Q(s,a)价值。4x12各state,4个actionfor a in range(4):qsa = 0for res in self.env.P[s][a]:p, next_state, r, done = res# 🌟这里在计算action valueqsa += p * (r + self.gamma * self.v[next_state] * (1 - done))# 本章环境比较特殊,奖励和下一个状态有关,所以需要和状态转移概率相乘qsa_list.append(self.pi[s][a] * qsa)# 🌟这里更新state valuenew_v[s] = sum(qsa_list) # 状态价值函数和动作价值函数之间的关系max_diff = max(max_diff, abs(new_v[s] - self.v[s])) #这里判断阈值是否继续进行迭代self.v = new_vif max_diff < self.theta: break # 满足收敛条件,退出评估迭代cnt += 1print("策略评估进行%d轮后完成" % cnt)def policy_improvement(self): # 策略提升for s in range(self.env.nrow * self.env.ncol):qsa_list = []for a in range(4):qsa = 0for res in self.env.P[s][a]:p, next_state, r, done = resqsa += p * (r + self.gamma * self.v[next_state] * (1 - done))qsa_list.append(qsa)maxq = max(qsa_list) #🌟选取当前state下maxQ(s,a)cntq = qsa_list.count(maxq) # 计算有几个动作得到了最大的Q值# 让这些动作均分概率,考虑到了最大qsa可能存在多个的情况self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]print("策略提升完成")return self.pidef policy_iteration(self): # 策略迭代while 1:self.policy_evaluation()old_pi = copy.deepcopy(self.pi) # 将列表进行深拷贝,方便接下来进行比较new_pi = self.policy_improvement()print_agent(agent, action_meaning, list(range(37, 47)), [47])if old_pi == new_pi: breakdef print_agent(agent, action_meaning, disaster=[], end=[]):print("状态价值:")for i in range(agent.env.nrow):for j in range(agent.env.ncol):# 为了输出美观,保持输出6个字符print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')print()print("策略:")for i in range(agent.env.nrow):for j in range(agent.env.ncol):# 一些特殊的状态,例如悬崖漫步中的悬崖if (i * agent.env.ncol + j) in disaster:print('****', end=' ')elif (i * agent.env.ncol + j) in end: # 目标状态print('EEEE', end=' ')else:a = agent.pi[i * agent.env.ncol + j]pi_str = ''for k in range(len(action_meaning)):pi_str += action_meaning[k] if a[k] > 0 else 'o' #action存在概率就打印print(pi_str, end=' ')print()env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001 #policy iteration的迭代终止的阈值判断
gamma = 0.9
agent = PolicyIteration(env, theta, gamma)
agent.policy_iteration()
# print_agent(agent, action_meaning, list(range(37, 47)), [47])
2.2.3运行结果
策略评估进行60轮后完成
策略提升完成
状态价值:
-27.23 -28.51 -29.62 -30.30 -30.63 -30.71 -30.57 -30.14 -29.22 -27.47 -24.65 -21.45
-33.63 -36.89 -38.79 -39.68 -40.04 -40.13 -40.01 -39.59 -38.59 -36.33 -31.53 -23.34
-47.27 -58.58 -61.78 -62.77 -63.10 -63.17 -63.09 -62.79 -61.93 -59.42 -51.38 -22.98
-66.15 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
^o<o oo<o oo<o oo<o oo ooo> ooo> ooo> ooo> ooo> ^oo>
^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ooo> ^ooo
^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ^ooo ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
策略评估进行72轮后完成
策略提升完成
状态价值:
-10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00
-10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00
-10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -10.00 -1.900 -1.000
-10.00 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
^v<> ^v<> ^v<> ^v<> ooo> ^vo> ^v<> ^v<> ^v<> ^v<> ^v<> ^v<>
^v<> ^v<> ^v<> ^v<> ooo> ^vo> ^v<> ^v<> ^v<> ^v<> ovoo ovoo
^v<> ^o<> ^o<> ^o<> ooo> ^oo> ^o<> ^o<> ^o<> ooo> ooo> ovoo
^v<o **** **** **** **** **** **** **** **** **** **** EEEE
策略评估进行44轮后完成
策略提升完成
状态价值:
-9.934 -9.902 -9.826 -9.678 -9.405 -9.338 -9.168 -8.718 -7.913 -6.729 -5.429 -4.817
-9.934 -9.898 -9.816 -9.657 -9.357 -9.285 -9.075 -8.499 -7.363 -5.390 -2.710 -1.900
-9.937 -9.891 -9.800 -9.622 -9.280 -9.200 -8.935 -8.173 -6.474 -2.710 -1.900 -1.000
-9.954 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo ovoo ovoo
ooo> ooo> ooo> ooo> ovoo ooo> ooo> ooo> ooo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
策略评估进行12轮后完成
策略提升完成
状态价值:
-7.712 -7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
策略评估进行1轮后完成
策略提升完成
状态价值:
-7.712 -7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
2.2.4代码流程概述
(1)创建环境
env = CliffWalkingEnv()
设置环境行列数,以及设置环境奖励及状态转移概率,都存存储在P(3维list[48,1,4])中,其中最小元组代表(s,a)对的信息(P[s][a] = [(p, next_state, reward, done)]),即状态转移概率、下一状态、即时奖励、是否完成标志(掉入悬崖或走至终点都视为“完成”)。
(2)设置参数
theta = 0.001 #policy iteration的迭代终止的阈值判断
gamma = 0.9
theta为PE过程停止的阈值判断,即“if max_diff < self.theta: break”,gamma 为奖励折扣率。
(3)价值评估(PE)
def policy_evaluation(self): # 策略评估cnt = 1 # 计数器while 1:max_diff = 0new_v = [0] * self.env.ncol * self.env.nrowfor s in range(self.env.ncol * self.env.nrow):qsa_list = [] # 开始计算状态s下的所有Q(s,a)价值。4x12各state,4个actionfor a in range(4):qsa = 0for res in self.env.P[s][a]:p, next_state, r, done = res# 🌟这里在计算action valueqsa += p * (r + self.gamma * self.v[next_state] * (1 - done))# 本章环境比较特殊,奖励和下一个状态有关,所以需要和状态转移概率相乘qsa_list.append(self.pi[s][a] * qsa)# 🌟这里更新state valuenew_v[s] = sum(qsa_list) # 状态价值函数和动作价值函数之间的关系max_diff = max(max_diff, abs(new_v[s] - self.v[s])) #这里判断阈值是否继续进行迭代self.v = new_vif max_diff < self.theta: break # 满足收敛条件,退出评估迭代cnt += 1print("策略评估进行%d轮后完成" % cnt)
①遍历所有(s,a),计算q(s,a),再累加得到v(s)=Σq(s,a)
v π k ( j + 1 ) ( s ) = ∑ a π k ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π k ( j ) ( s ′ ) ] v_{\pi_{k}}^{(j+1)}(s)=\sum_{a}\pi_{k}(a|s)\left[\sum_{r}p(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v_{\pi_{k}}^{(j)}(s')\right] vπk(j+1)(s)=∑aπk(a∣s)[∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπk(j)(s′)]
等同于
q π ( s , a ) = ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) \begin{aligned}q_\pi(s,a)=\sum_rp(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v_\pi(s')\end{aligned} qπ(s,a)=r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)
v π ( s ) = ∑ a π ( a ∣ s ) q π ( s , a ) v_{\pi}(s)=\sum_{a}\pi(a|s)q_{\pi}(s,a) vπ(s)=∑aπ(a∣s)qπ(s,a)
②通过比较max_diff 和theta 的差值,判断是否完成策略评估
(4)策略提升(PI)
def policy_improvement(self): # 策略提升for s in range(self.env.nrow * self.env.ncol):qsa_list = []for a in range(4):qsa = 0for res in self.env.P[s][a]:p, next_state, r, done = resqsa += p * (r + self.gamma * self.v[next_state] * (1 - done))qsa_list.append(qsa)maxq = max(qsa_list) #🌟选取当前state下maxQ(s,a)cntq = qsa_list.count(maxq) # 计算有几个动作得到了最大的Q值# 让这些动作均分概率,考虑到了最大qsa可能存在多个的情况self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]print("策略提升完成")return self.pi
①遍历所有(s,a),根据PE估计的v(s)值计算各q(s,a)值
②根据q(s,a)优化policy,若存在q(s,a)相同的情况,则policy中多个action概率相等
a k ∗ ( s ) = arg max a q π k ( s , a ) a_{k}^{*}(s)=\arg\max_{a}q_{\pi_{k}}(s,a) ak∗(s)=argmaxaqπk(s,a)
(5)终止判断
if old_pi == new_pi: break
最近两次policy一致时,终止循环。
2.3价值迭代(value iteration)算法
2.3.1伪代码

- 算法流程简述:
①值初始化:根据环境,初始化各state的state value,一般设置为0
②更新Q值:进入循环,根据bellman方程计算各state下所有action的action value
③策略更新(policy update):以最大的action value更新policy(greedy policy)
④价值更新(value update):估计新一轮的state value
⑤阈值判断:判断最近两轮的state value差值是否小于阈值,若是则跳出循环输出policy;若否则继续重复②~④步
2.3.2完整代码
import copyclass CliffWalkingEnv:""" 悬崖漫步环境"""def __init__(self, ncol=12, nrow=4):self.ncol = ncol # 定义网格世界的列self.nrow = nrow # 定义网格世界的行# 转移矩阵P[state][action] = [(p, next_state, reward, done)]包含下一个状态和奖励self.P = self.createP()def createP(self):# =============================================================================
# 转移矩阵P[s][a] = [(p, next_state, reward, done)]包含下一个状态和奖励
# p:s到next_state的状态转移概率,在这里都取1
# reward:s到next_state的即时奖励
# done:是否到达终点或悬崖
# =============================================================================# 初始化P = [[[] for j in range(4)] for i in range(self.nrow * self.ncol)]# 4种动作, change[0]:上,change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)# 定义在左上角change = [[0, -1], [0, 1], [-1, 0], [1, 0]]for i in range(self.nrow):for j in range(self.ncol):for a in range(4):# 位置在悬崖或者目标状态,因为无法继续交互,任何动作奖励都为0if i == self.nrow - 1 and j > 0:# 除了4行1列的元素的done状态都设置为True,其都为悬崖,除4行12列为终点P[i * self.ncol + j][a] = [(1, i * self.ncol + j, 0,True)]continue# 其他位置next_x = min(self.ncol - 1, max(0, j + change[a][0]))next_y = min(self.nrow - 1, max(0, i + change[a][1]))next_state = next_y * self.ncol + next_xreward = -1done = False# 下一个位置在悬崖或者终点if next_y == self.nrow - 1 and next_x > 0:done = Trueif next_x != self.ncol - 1: # 下一个位置在悬崖reward = -100P[i * self.ncol + j][a] = [(1, next_state, reward, done)]return Pclass ValueIteration:""" 价值迭代算法 """def __init__(self, env, theta, gamma):self.env = envself.v = [0] * self.env.ncol * self.env.nrow # 初始化价值为0self.theta = theta # 价值收敛阈值self.gamma = gamma# 价值迭代结束后得到的策略self.pi = [None for i in range(self.env.ncol * self.env.nrow)]def value_iteration(self):cnt = 0while 1:max_diff = 0new_v = [0] * self.env.ncol * self.env.nrowfor s in range(self.env.ncol * self.env.nrow):qsa_list = [] # 开始计算状态s下的所有Q(s,a)价值for a in range(4):qsa = 0for res in self.env.P[s][a]:p, next_state, r, done = resqsa += p * (r + self.gamma * self.v[next_state] * (1 - done))qsa_list.append(qsa) # 这一行和下一行代码是价值迭代和策略迭代的主要区别new_v[s] = max(qsa_list)max_diff = max(max_diff, abs(new_v[s] - self.v[s]))self.v = new_vif max_diff < self.theta: break # 满足收敛条件,退出评估迭代cnt += 1print("价值迭代一共进行%d轮" % cnt)self.get_policy()def get_policy(self): # 根据价值函数导出一个贪婪策略for s in range(self.env.nrow * self.env.ncol):qsa_list = []for a in range(4):qsa = 0for res in self.env.P[s][a]:p, next_state, r, done = resqsa += p * (r + self.gamma * self.v[next_state] * (1 - done))qsa_list.append(qsa)maxq = max(qsa_list)cntq = qsa_list.count(maxq) # 计算有几个动作得到了最大的Q值# 让这些动作均分概率self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]def print_agent(agent, action_meaning, disaster=[], end=[]):print("状态价值:")for i in range(agent.env.nrow):for j in range(agent.env.ncol):# 为了输出美观,保持输出6个字符print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')print()print("策略:")for i in range(agent.env.nrow):for j in range(agent.env.ncol):# 一些特殊的状态,例如悬崖漫步中的悬崖if (i * agent.env.ncol + j) in disaster:print('****', end=' ')elif (i * agent.env.ncol + j) in end: # 目标状态print('EEEE', end=' ')else:a = agent.pi[i * agent.env.ncol + j]pi_str = ''for k in range(len(action_meaning)):pi_str += action_meaning[k] if a[k] > 0 else 'o' #action存在概率就打印print(pi_str, end=' ')print()env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001
gamma = 0.9
agent = ValueIteration(env, theta, gamma)
agent.value_iteration()
print_agent(agent, action_meaning, list(range(37, 47)), [47])
2.3.3运行结果
价值迭代一共进行14轮
状态价值:
-7.712 -7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
2.4截断策略迭代(Truncated policy iteration)
2.4.1伪代码

在policy iteration的基础上增加了一个截断因子j,用于提升PE的效率,最终也能收敛。
小结
- 动态规划算法是强化学习的基础,其中应用的贝尔曼方程是估计state value,action value的“渠道”
- 必须是在“白盒”环境下应用,即为model-based算法,适用范围有限
- Truncated policy iteration中,截断步数取1,即为value iteration;截断步数取∞,即为policy iteration
相关文章:

【动手学强化学习】part2-动态规划算法
阐述、总结【动手学强化学习】章节内容的学习情况,复现并理解代码。 文章目录 一、什么是动态规划?1.1概念1.2适用条件 二、算法示例2.1问题建模2.2策略迭代(policyiteration)算法2.2.1伪代码2.2.2完整代码2.2.3运行结果2.2.4代码…...

【python爬虫实战】爬取全年天气数据并做数据可视化分析!附源码
由于篇幅限制,无法展示完整代码,需要的朋友可在下方获取!100%免费。 一、主题式网络爬虫设计方案 1. 主题式网络爬虫名称:天气预报爬取数据与可视化数据 2. 主题式网络爬虫爬取的内容与数据特征分析: - 爬取内容&am…...

初识Linux · 动静态库(incomplete)
目录 前言: 静态库 动态库 前言: 继上文,我们从磁盘的理解,到了文件系统框架的基本搭建,再到软硬链接部分,我们开始逐渐理解了为什么运行程序需要./a.out了,这个前面的.是什么我们也知道了。…...

华为OD机试 - 匿名信(Java 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(E卷D卷A卷B卷C卷)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加…...
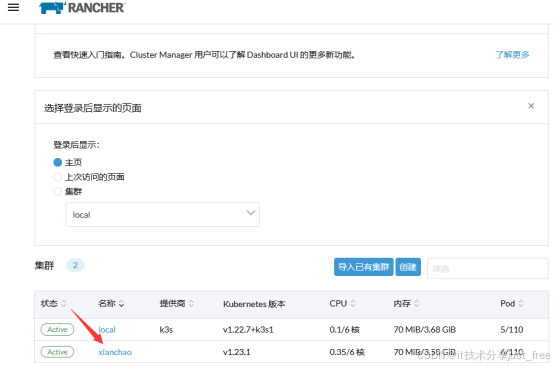
通过rancher2.7管理k8s1.24及1.24以上版本的k8s集群
目录 初始化实验环境 安装Rancher 登录Rancher平台 通过Rancher2.7管理已存在的k8s最新版集群 文档中的YAML文件配置直接复制粘贴可能存在格式错误,故实验中所需要的YAML文件以及本地包均打包至网盘. 链接:https://pan.baidu.com/s/1oYX4eGoBtW_R-7i…...

text-align的属性justify
text-align常用的属性是left、center、right,具体的可参考css解释,今天重点记录的对象是justify justify 可以使文本的两端都对齐在两端对齐文本中,文本行的左右两端都放在父元素的内边界上。然后,调整单词和字母间的间隔&#x…...

使用python自制桌面宠物,好玩!——枫原万叶桌宠,可以直接打包成exe去跟朋友炫耀。。。
大家好,我是小黄。 今天我们使用python实现一个桌面宠物。只需要gif动态图片就行。超级简单容易上手。 #完整源代码可在下方图片免费获取 一:下载相关的库文件。 我们本次使用到的库文件为:tkinter和pyautogui 下载命令: pip…...
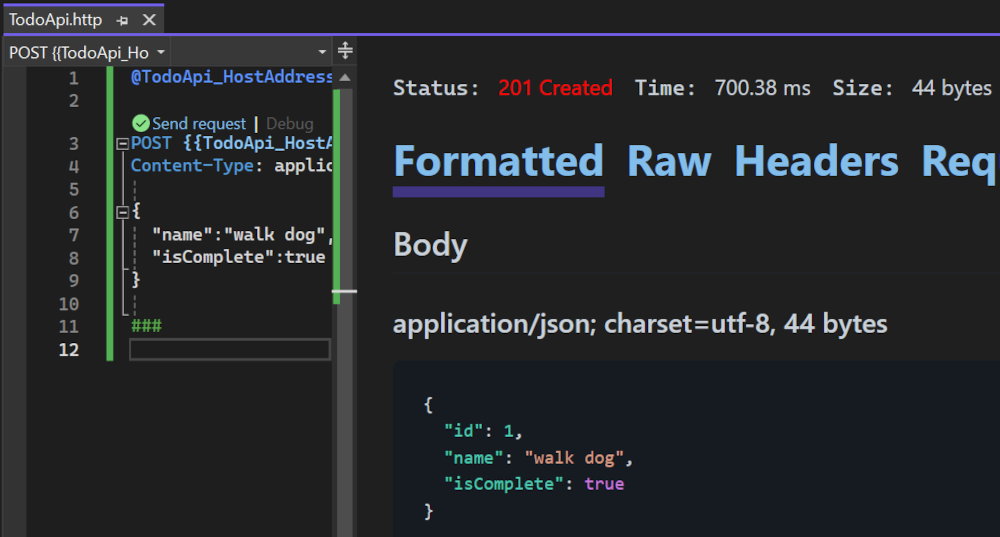
使用 ASP.NET Core 8.0 创建最小 API
构建最小 API,以创建具有最小依赖项的 HTTP API。 它们非常适合需要在 ASP.NET Core 中仅包括最少文件、功能和依赖项的微服务和应用。 本教程介绍使用 ASP.NET Core 生成最小 API 的基础知识。 在 ASP.NET Core 中创建 API 的另一种方法是使用控制器。 有关在最小 …...
气候服务平台ClimateSERV2.0简介(python)
1 简介 ClimateSERV 2.0允许开发从业者、科学家/研究人员和政府决策者可视化和下载历史降雨数据、植被状况数据以及 180 天的降雨和温度预报,以增进对农业和水资源供应相关问题的理解并做出改进的决策。 这些数据可以通过 Web 应用程序直接访问,也可以…...

Docker | centos7上对docker进行安装和配置
安装docker docker配置条件安装地址安装步骤2. 卸载旧版本3. yum 安装gcc相关4. 安装需要的软件包5. 设置stable镜像仓库6. 更新yum软件包索引7. 安装docker引擎8. 启动测试9. 测试补充:设置国内docker仓库镜像 10. 卸载 centos7安装docker https://docs.docker.com…...

React--》掌握Valtio让状态管理变得轻松优雅
Valtio采用了代理模式,使状态管理变得更加直观和易于使用,同时能够与React等框架无缝集成,本文将深入探讨Valtio的核心概念、使用场景以及其在提升应用性能中的重要作用,帮助你掌握这一强大工具,从而提升开发效率和用户…...

python爬虫百度图片
直接给代码,可直接用,个人需要修改的地方有两处: self.directory 这是本地存储地址,修改为自己电脑的地址,另外,**{}**不要删spider.json_count 10 这是下载的图像组数,一组有30张图像&#x…...
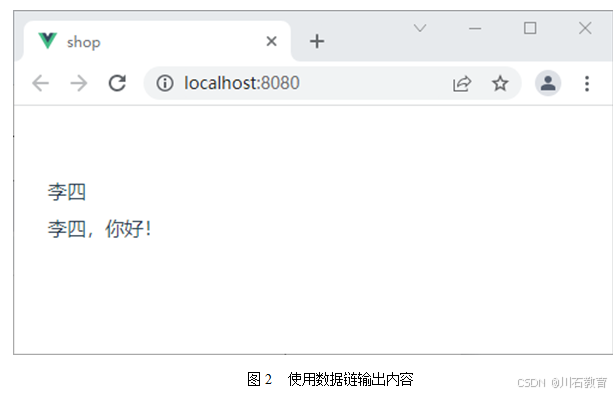
前端开发:Vue中数据绑定原理
Vue 中最大的一个特征就是数据的双向绑定,而这种双向绑定的形式,一方面表现在元数据与衍生数据之间的响应,另一方面表现在元数据与视图之间的响应,而这些响应的实现方式,依赖的是数据链,因此,要…...

CTF-RE 从0到N: TEA
TEA TEA(Tiny Encryption Algorithm,轻量加密算法) 是一种简单、快速的对称加密算法。它是一个分组加密算法,通常用于加密 64 位的数据块,并使用 128 位的密钥。TEA 是一种“费斯妥结构”(Feistel structu…...

python 使用PIL获取图片长宽
在Python中,你可以使用Pillow库(PIL的一个分支和替代品)来获取图片的长和宽。Pillow提供了丰富的图像处理功能,包括获取图像的基本属性,如尺寸。 以下是一个简单的示例,展示了如何使用Pillow库来获取图片的…...
【Nas】X-DOC:搞机之PVE部署All In One(黑群晖NAS 软路由OpenWrt Docker Win10远程桌面)
【Nas】X-DOC:搞机之PVE部署All In One(黑群晖NAS & 软路由OpenWrt & Docker & Win10远程桌面) 1、原硬件配置清单:2、改AIO后增加配置清单:3、虚拟化平台PVE:4、搭建的关键服务: 1…...

linux 驱动源码分析的理解。
首先 , 是linux 驱动,我看网上的老师,在分析源码时 , 不会 所有的函数都分析,而是分析一些比较重要的函数,一些厉害的人,在分析源码时…...

鸿蒙-任务栏右击退出 或 UIAbility窗口关闭,怎么弹框拦截
onPrepareToTerminate 需要配置权限 ohos.permission.PREPARE_APP_TERMINATE 参考链接:文档中心import { emitter } from kit.BasicServicesKit; import { common } from kit.AbilityKit; import { TipsDialog } from kit.ArkUI;// entryAbility.ets 在你的uiabilit…...

【C++进阶篇】——STL的简介
【C进阶篇】——STL的简介 1.什么是STL STL(standard template libaray-标准模板库):是C标准库的重要组成部分,不仅是一个可复用的组件库,而且是一个包罗数据结构与算法的软件框架。 2.STL的版本 原始版本 Alexander Stepanov、Meng Lee 在…...

信息安全工程师(70)网络攻击陷阱技术与应用
前言 网络攻击陷阱技术是一种主动的防御方法,作为网络安全的重要策略和技术手段,有利于网络安全管理者获得信息优势。 一、网络攻击陷阱技术原理 网络攻击陷阱技术可以消耗攻击者所拥有的资源,加重攻击者的工作量,迷惑攻击者&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
