【数据结构】快速排序(三种实现方式)
目录
一、基本思想
二、动图演示(hoare版)
三、思路分析(图文)
四、代码实现(hoare版)
五、易错提醒
六、相遇场景分析
6.1 ❥ 相遇位置一定比key要小的原因
6.2 ❥ 右边为key,左边先走
6.3 ❥ 一边为key,另一边先走的原因
七、时间复杂度分析
八、快排的优化
8.1 ❥ key值的选取
8.1.1 随机数选key
8.1.2 三数取中
8.2 ❥ 小区间优化
九、挖坑法
9.1 ❥ 动图演示
9.2 ❥ 思路详解
9.3 ❥ 代码实现
十、前后指针法
10.1 ❥ 动图演示
10.2 ❥ 思路详解
10.3 ❥ 代码实现
一、基本思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。
其基本思想为:
- 任取待排序元素序列中的某元素作为基准值,按照该排序将待排序集合分割成两个子序列
- 左子序列中所有元素均小于基准值,右子序列中的所有元素均大于基准值
- 然后分别对左右两部分重复上述操作,直到将无序序列排列成有序序列。
二、动图演示(hoare版)

三、思路分析(图文)
以下以升序为例:








简言之,就是先进行单趟的排序,单趟排完之后,key已经放在它合适的位置上,分割出了一个左区间和右区间,然后进行递归排序,当左右区间都有序时,那么就整体有序。

四、代码实现(hoare版)
void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//hoare版
void QuickSort(int* a, int left, int right) //参数为数组下标
{//递归结束条件 if (left >= right){return;}int keyi = left;int begin = left;int end = right;//单趟排序while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}swap(&a[begin], &a[end]);}swap(&a[begin], &a[keyi]);keyi = begin; //将begin下标位置赋给keyi//分割出左右区间// [left, keyi-1] keyi [keyi+1, right]//整体排序 递归QuickSort(a, left, keyi - 1);QuickSort(a, keyi+1,right);}五、易错提醒
我们看如下一段代码:
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = left;int begin = left;int end = right;while (begin < end){while (a[end] >= a[keyi]){end--;}while (a[begin] <= a[keyi]){begin++;}swap(&a[begin], &a[end]);}swap(&a[begin], &a[keyi]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
上述代码是有问题存在的
通过调试可知,第二个while遇到相遇要停止,这里while少了相遇停止条件,否则可能会一直死循环下去
为何要创建begin和end?
通过上述思路分析易知,区间的每次分割,left都需要指向原始序列第一个元素的位置,right指向原始序列最后一个元素的位置,所以这里专门定义一个begin和end 而不是用left和right去++ --,就是为了便于分割区间。
六、相遇场景分析
6.1 ❥ 相遇位置一定比key要小的原因
我们发现,每次L与R相遇时与key进行交换时,L的值都小于key,这是为什么呢?
这里对他们相遇的场景进行分析:
相遇时无非两种场景,要么R遇见L,要么L遇见R
L遇R:
R先走,找小,停下来。
R停下条件是:遇见比key小的值,R停的位置一定比key小,L没有找到大的,遇见R停下
所以说:L遇R,它们相遇的位置就是R的位置

R遇L:
R先走,找小,没有找到比key小的,直接跟L相遇了。
L停留的位置是上一轮交换的位置
上一轮交换,把比key小的值,换到了L的位置

6.2 ❥ 右边为key,左边先走
我们发现,上面相遇场景都是左边做key,如果右边做key,让左边先走呢?
右边做key时:相遇位置一定比key要大
如下图所示:

结论:
- 左边做key,右边先走,可以保证相遇位置一定比key小
- 右边做key,左边先走,可以保证相遇位置一定比key大
6.3 ❥ 一边为key,另一边先走的原因
有人肯定会疑惑,为什么要一边做key,另一边先走,不可以做key的一边先走吗?
可以验证一下:

上图是让key在左边,且左边先走,在8相遇,然后与key==5进行交换
交换完后,5换到了数组下标为5的位置,并没有换到他所对应的正确位置,且左区间的8比5大。
我们知道,快排是当一趟排完之后,左区间都比key小,右区间都比key大,且key刚好在正确位置上,这样才可以继续分左右区间进行递归排序。
因此,不可以做key的一边先走
结论:一边做key,只能让另一边先走
七、时间复杂度分析
在比较理想的情况下,快排的递归结构接近完全二叉树,所以层数为logn层,每一层排序次数近似为n,(即单趟的时间复杂度为n)
故时间复杂度为:O(nlogn)

但是在有序场景下使用快排会性能会下降,时间复杂度为O(N^2)
如下图所示:
- 当key在左边时,右边R找小就会找不到,然后一直往左走,直到在key处相遇,
- 然后自己跟自己交换,结束一趟的排序。分割出左右区间。
- 此处没有左区间,只存在右区间
- 就这样依次类推......
- 那么总共执行的次数就会是一个等差数列
- 即:时间复杂度为O(N^2)
- 它的效率就会大幅度降低。

八、快排的优化
- 经过时间复杂度的分析,发现当前的快排算法还是存在一些缺陷的,那就是在有序场景下使用快排会性能会下降,此外,还有可能导致栈溢出。
- 为什么在有序场景下会发生栈溢出?
- 因为每走一层就是一个递归,这里递归的深度太深会有栈溢出的风险。
- 所以快排在此还是有较为明显的缺陷的,面对这些缺陷,我们在此应怎么解决呢?
- 我们知道,时间复杂度为O(nlogn)的前提是每次区间的划分都是二分,也就是每次选择交换的key,都是接近中间位置的值,哪怕不那么接近二分,但整体深度是logn就可以
- 所以key值的选取非常关键,如果固定的选择最左边(下标为0)的值,就有可能选到最小的值,然后出现效率退化栈溢出的风险
- 那如何选key才能避免有序的情况下效率退化呢?
- 下面提供了两种选取key值的方式
8.1 ❥ key值的选取
8.1.1 随机数选key
- 如果想要输出给定范围[a,b]内的随机数,需要使用rand()%(b-a+1)+a
- 缺陷:可能刚刚好选到最大或者最小值
代码如下:
void rand_key(int* a, int left, int right)
{int randi = left + (rand() % (right - left + 1));swap(&a[left], &a[randi]);
}8.1.2 三数取中
所谓三数取中,就是从最左边,最右边,最中间三个位置,选择中间的值(不大不小的值)作为key(赋值给key)
代码如下:
int GetMidi(int* a, int left, int right)
{int midi = (left + right) / 2;if (a[left] > a[right]){if (a[left] < a[midi]) // r<l<m{return left;}else if(a[midi]<a[right]) //m<r<l{return right;}else //r<m<l{return midi;}}else{if (a[right]<a[midi]) //l<r<m{return right;}else if (a[midi]<a[left]) //m<l<r{return left;}else //l<m<r{return midi;}}
}注意
这里是选出的中间值还应跟最左边的值进行交换,还应该让最左边的值作为key

8.2 ❥ 小区间优化
为何要有小区间优化:
当将一组待排序列进行快排,递归到只剩下5个值时,我们还要进行选key,分割左右区间等操作让5个值有序,此刻使用递归调用花费代价太大(最后一层递归调用就要占整体递归调用的50%),这就引入了小区间优化的方式。
小区间优化目的:
当待排区间长度小于等于某个阈值时,不再递归分割排序,减少递归调用的深度和对栈空间的使用,避免过度分割导致的效率下降,可以在处理小规模数据时获得更好的性能,从而提高整体排序算法的效率。
思路分析:
- 这里选择直接插入排序,首先希尔排序适合数据量较大时使用,这里不适合使用。
- 直接插入排序在同是O(N^2)的情况下,它的速度要更快
- 因为通常情况下,它是达不到O(N^2),只有在完全有序的情况下,才能达到O(N^2)
- 所以同级情况下,它要比其它排序更快一点,它的实践意义也在于此。
- 当然,引入小区间优化会使得效率低下,增加了算法的复杂度。
代码如下:
//直接插入算法
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]) {a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}//交换算法
void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//三数取中
int GetMidi(int* a, int left, int right)
{int midi = (left + right) / 2;if (a[left] > a[right]){if (a[left] < a[midi]) {return left;}else if (a[midi] < a[right]) {return right;}else {return midi;}}else{if (a[right] < a[midi]) {return right;}else if (a[midi] < a[left]) {return left;}else {return midi;}}
}//hoare版
void QuickSort(int* a, int left, int right) //参数为数组下标
{if (left >= right){return;}// 小区间优化,不再递归分割排序,减少递归的次数if ((right - left + 1) < 10){InsertSort(a + left, right - left + 1);}else{//三数取中int midi = GetMidi(a, left, right);swap(&a[left], &a[midi]);int keyi = left;int begin = left;int end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}swap(&a[begin], &a[end]);}swap(&a[begin], &a[keyi]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}九、挖坑法
这里的挖坑法是以单趟排序的思路优化出的挖坑法。
该方法没有效率的提升(因为单趟排序效率无提升空间,至少都得遍历一遍)
但理解起来更简单,因为它们相遇的位置是坑,所以不用分析左边做key,右边先走的问题,也不用分析相遇位置比key小的原因
9.1 ❥ 动图演示

9.2 ❥ 思路详解
- 将序列的第一个元素作为基准值,存放在临时变量key中,此时的第一个坑位形成
- L指向第一个元素,R指向最后一个元素
- R开始向前移动,R--,找比key小的值,找到后,将R指向的值填入L的坑位,此时R形成一个坑位
- 然后L开始向后移动,L++,找比key大的值,找到后,将L指向的值填入R的坑位,此时L形成一个坑位
- R和L交错移动,形成新的坑位,直到R与L相遇
- 此时将key值填入L和R共同所指向的坑位
- 单趟排序完成
- 然后分割左右区间进行递归排序
- 最后排成一个有序序列

9.3 ❥ 代码实现
//挖坑法
void QuickSort1(int*a,int left,int right)
{//递归结束条件 if (left >= right){return;}int key = a[left];int begin = left;int end = right;//单趟排序while (begin < end){while (begin<end&&a[end] >= key){end--;}a[begin] = a[end]; //甩给右区间坑while (begin<end&&a[begin] <= key){begin++;}a[end] = a[begin]; //甩给左区间坑}a[begin] = key; //将key填入相遇的坑//进行递归排序QuickSort1(a, left, begin - 1);QuickSort1(a, begin + 1, right);}
十、前后指针法
前后指针法只是单趟逻辑改变,整体递归思路并没有改变。
该方法没有效率的提升。
10.1 ❥ 动图演示

10.2 ❥ 思路详解
- 将key指向序列的第一个元素,设为基准值
- prev指向key的位置,cur指向prev的下一个位置
- 对cur进行判断:
如果cur>=key,则cur++
如果cur<key,prev++,交换cur和prev所指向的值,然后cur++
- 再对cur进行判断,直到cur++到序列的最后一个元素的下一个位置,交换prev与key的值
- 此时单趟排序完成
- 然后分割左右区间进行递归排序
- 最后排成一个有序序列

10.3 ❥ 代码实现
void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//前后指针法
void QuickSort2(int* a, int left, int right)
{if (left >= right){return;}//单趟排序int keyi = left;int prev = left;int cur = left + 1;while (cur<=right){if (a[cur] < a[keyi]) //cur的值比keyi的值小{prev++;if (prev != cur) //判断prev与cur是否指向同一位置{swap(&a[prev], &a[cur]);}}cur++;}swap(&a[prev], &a[keyi]);QuickSort2(a, left, prev - 1);QuickSort2(a, prev + 1, right);}相关文章:

【数据结构】快速排序(三种实现方式)
目录 一、基本思想 二、动图演示(hoare版) 三、思路分析(图文) 四、代码实现(hoare版) 五、易错提醒 六、相遇场景分析 6.1 ❥ 相遇位置一定比key要小的原因 6.2 ❥ 右边为key,左边先走 …...
)
利用前向勾子获取神经网络中间层的输出并将其进行保存(示例详解)
代码示例: # 激活字典,用于保存每次的中间特征 activation {}# 将 forward_hook 函数定义在 upsample_v2 外部 def forward_hook(name):def hook(module, input, output):activation[name] output.detach()return hookdef upsample_v2(in_channels, o…...

CTF-RE 从0到N: S盒
S盒(Substitution Box) 是密码学中的一种替换表,用于对输入数据进行非线性变换,以增加加密过程的复杂性。它主要用于对称加密算法中(例如AES、DES),作为加密轮次的一部分,对输入字节…...
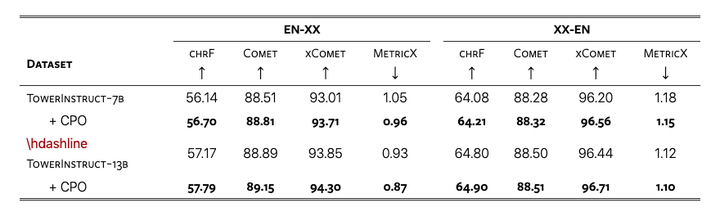
MT-Pref数据集:包含18种语言的18k实例,涵盖多个领域。实验表明它能有效提升Tower模型在WMT23和FLORES基准测试中的翻译质量。
2024-10-10,由电信研究所、里斯本大学等联合创建MT-Pref数据集,它包含18种语言方向的18k实例,覆盖了2022年后的多个领域文本。通过在WMT23和FLORES基准测试上的实验,我们展示了使用MT-Pref数据集对Tower模型进行对齐可以显著提高翻…...

【C++ 真题】B2099 矩阵交换行
矩阵交换行 题目描述 给定一个 5 5 5 \times 5 55 的矩阵(数学上,一个 r c r \times c rc 的矩阵是一个由 r r r 行 c c c 列元素排列成的矩形阵列),将第 n n n 行和第 m m m 行交换,输出交换后的结果。 输入格式 输入共 6 6 6 …...
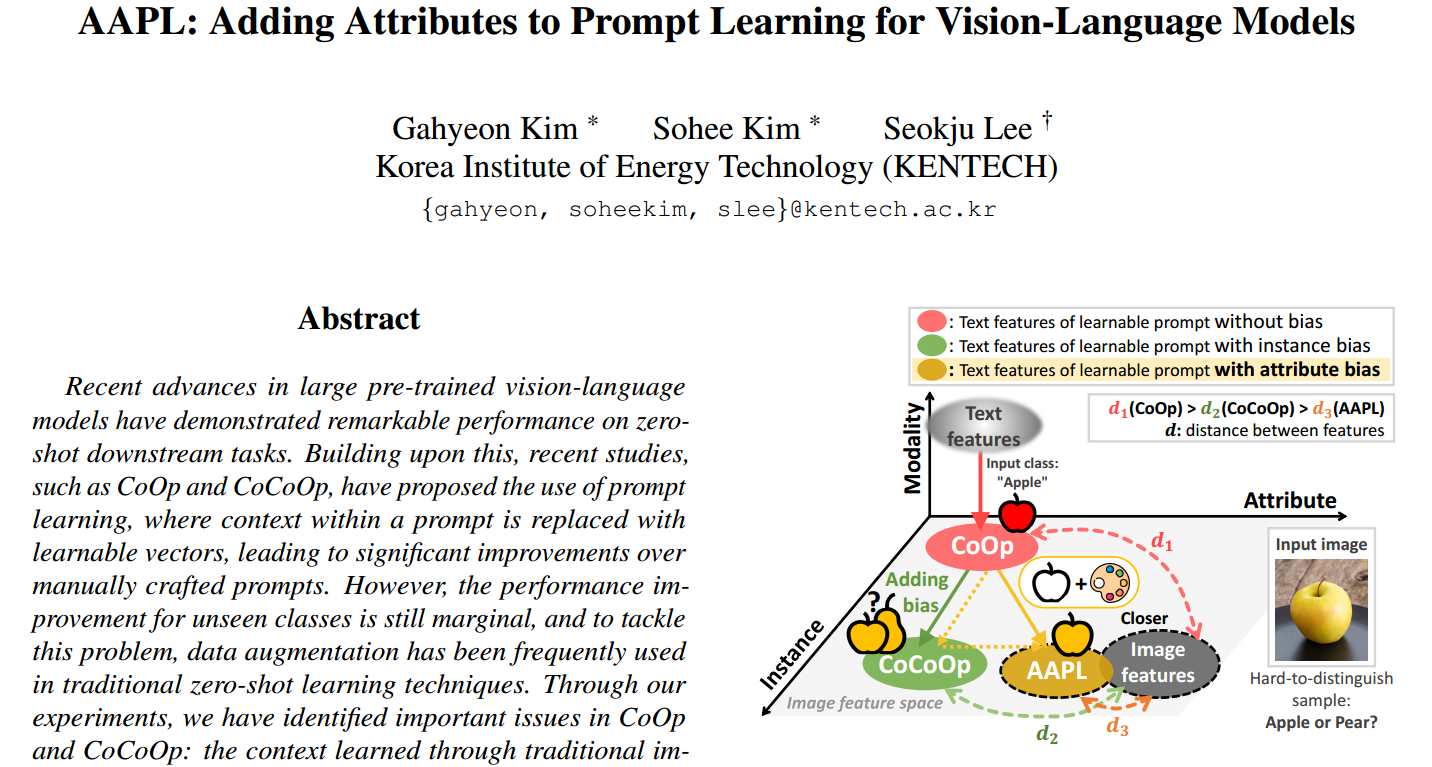
AAPL: Adding Attributes to Prompt Learning for Vision-Language Models
文章汇总 当前的问题 1.元标记未能捕获分类的关键语义特征 如下图(a)所示, π \pi π在类聚类方面没有显示出很大的差异,这表明元标记 π \pi π未能捕获分类的关键语义特征。我们进行简单的数据增强后,如图(b)所示,效果也是如…...
)
MySQLDBA修炼之道-开发篇(一)
三、开发基础 1. 数据模型 1.1 关系数据模型介绍 关于NULL 如果某个字段的值是未知的或未定义的,数据库会提供一个特殊的值NULL来表示。NULL值很特殊,在关系数据库中应该小心处理。例如查询语句“select*from employee where 绩效得分<85 or>绩…...

Spring MVC 知识点全解析
Spring MVC 知识点全解析 Spring MVC 是一个基于 Java 的请求驱动的 Web 框架,属于 Spring 框架的一部分,广泛用于构建企业级 Web 应用程序。本文将详细阐述 Spring MVC 的核心知识点,包括其工作原理、关键组件、配置、请求处理、数据绑定、…...

python 基于FastAPI实现一个简易的在线用户统计 服务
简易在线用户统计服务 概述 这是一个基于Python的FastAPI框架实现的服务,用于统计客户端的心跳信息,并据此维护在线用户列表以及记录活跃用户数。 功能特性 心跳接收:接受来自客户端的心跳包,以更新客户端的状态。在线用户统计…...

glibc中xdr的一个bug
本人在64位linux服务器上(centos7),发现xdr_u_long这个函数有个bug,就是数字的范围如果超过unsigned int的最大值(4294967295)时,xdr_u_long失败。 这个场景主要用在unix时间戳上面,比如一款软件,设置有效期为100年。…...

Android Framework定制sim卡插入解锁pin码的界面
文章目录 手机设置SIM卡pin码一、安卓手机二、苹果手机 Android Framework中SIM卡pin码代码定位pin码提示文本位置定位pin码java代码位置 定制pin码framework窗口数字按钮 手机设置SIM卡pin码 设置 SIM 卡 PIN 码可以提高手机的安全性,防止他人在未经授权的情况下使…...

cc2530 Basic RF 讲解 和点灯讲解(1_1)
1. Basic RF 概述 Basic RF 是 TI 提供的一套简化版的无线通信协议栈,旨在帮助开发者快速搭建无线通信系统。它基于 IEEE 802.15.4 标准的数据包收发,但只用于演示无线设备数据传输的基本方法,不包含完整功能的协议。Basic RF 的功能限制包括…...

Android H5页面性能分析策略
文章目录 引言一、拦截资源加载请求以优化性能二、通过JavaScript代码监控资源下载速度三、使用vConsole进行前端性能调试四、使用Chrome DevTools调试Android端五、通过抓包分析优化网络性能六、总结 引言 在移动应用开发中,H5页面的性能直接影响到用户体验。本文…...

【前端面试】Typescript
Typescript面试题目回答 Typescript有哪些常用类型? Typescript的常用类型包括: 基本类型:boolean(布尔类型)、number(数字类型)、string(字符串类型)。特殊类型:nul…...
、手动管理(C语言)与所有权机制(Rust)(手动内存管理、手动管理内存))
程序语言的内存管理:垃圾回收GC(Java)、手动管理(C语言)与所有权机制(Rust)(手动内存管理、手动管理内存)
文章目录 程序语言的内存管理:垃圾回收、手动管理与所有权机制引言一、垃圾回收机制(GC)(Java)1. 什么是垃圾回收机制2. 垃圾回收的工作原理3. 优点与缺点4. 示例代码 二、手动管理内存的分配和释放(C语言&…...

研究生论文学习记录
文献检索 检索论文的网站 知网:找论文,寻找创新点paperswithcode :这个网站可以直接找到源代码 直接再谷歌学术搜索 格式:”期刊名称“ 关键词 在谷歌学术搜索特定期刊的关键词相关论文,可以使用以下几种方法&#…...

毕业设计选题:基于Django+Vue的图书馆管理系统
开发语言:Python框架:djangoPython版本:python3.7.7数据库:mysql 5.7数据库工具:Navicat11开发软件:PyCharm 系统展示 系统首页 图书馆界面 图书信息界面 个人中心界面 后台登录界面 管理员功能界面 用户…...

#网络安全#NGSOC与传统SOC的区别
NGSOC是Next Generation Security Operation Center(下一代安全运营中心)的缩写。 NGSOC安全运营服务基于态势感知与安全运营平台来开展监测分析等一系列的服务工作,旨在通过专业、高效的运营服务工作,帮助用户尽可能发挥NGSOC作…...

GCN+BiLSTM多特征输入时间序列预测(Pytorch)
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 GCNBiLSTM多特征输入时间序列预测(Pytorch) 可以做风电预测,光伏预测,寿命预测,浓度预测等。 Python代码,基于Pytorch编写 1.多特征输入单步预测…...

LinkedList和链表之刷题课(下)
1. 给定x根据x把链表分割,大的结点放在x后面,小的结点放在x前面 题目解析: 注意此时的pHead就是head(头节点的意思) 基本上就是给定一个链表,我们根据x的值来把这个链表分成俩部分,大的那部分放在x后面,小的那部分放在x前面,并且我们不能改变链表本来的顺序,比如下面的链表,我…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
