算法题总结（十九）——图论

图论

DFS框架

void dfs(参数) {
if (终止条件) {存放结果;return;
}for (选择：本节点所连接的其他节点) {处理节点;dfs(图，选择的节点); // 递归回溯，撤销处理结果
}
}

深搜三部曲

1. 确认递归函数，参数
2. 确认终止条件
3. 处理目前搜索节点出发的路径

797、所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

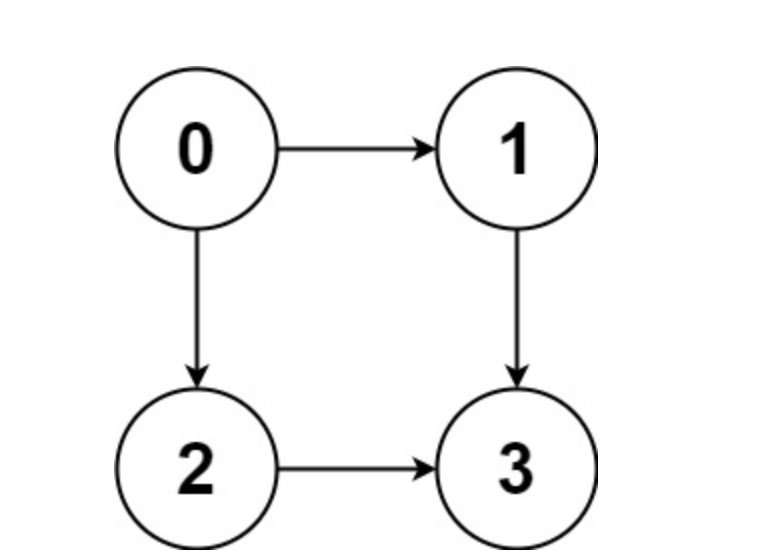
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

1、确认递归函数、参数

首先我们dfs函数一定要存一个图，用来遍历的，还要存一个目前我们遍历的节点，定义为x。

至于路径和路径集合，可以放在全局变量里。

2、确认终止条件

当目前遍历的节点 为 最后一个节点的时候，就找到了一条，从 出发点到终止点的路径。

3、处理目前搜索节点出发的路径

class Solution {List<List<Integer>> res =new ArrayList<>();List<Integer> path=new ArrayList<>();public void DFS(int[][] graph,int x){//说明找到了终点if(x==graph.length-1){res.add(new ArrayList<>(path));  //这里一定要建立一个新的return;}//遍历和x相连的结点for(int i=0;i<graph[x].length;i++){path.add(graph[x][i]);DFS(graph,graph[x][i]);path.remove(path.size()-1);  //回溯}}public List<List<Integer>> allPathsSourceTarget(int[][] graph) {//从头结点开始path.add(0);DFS(graph,0);return res;}
}

BFS框架

广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。

当然，也有一些问题是广搜 和 深搜都可以解决的，例如岛屿问题，这类问题的特征就是不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行

200、岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

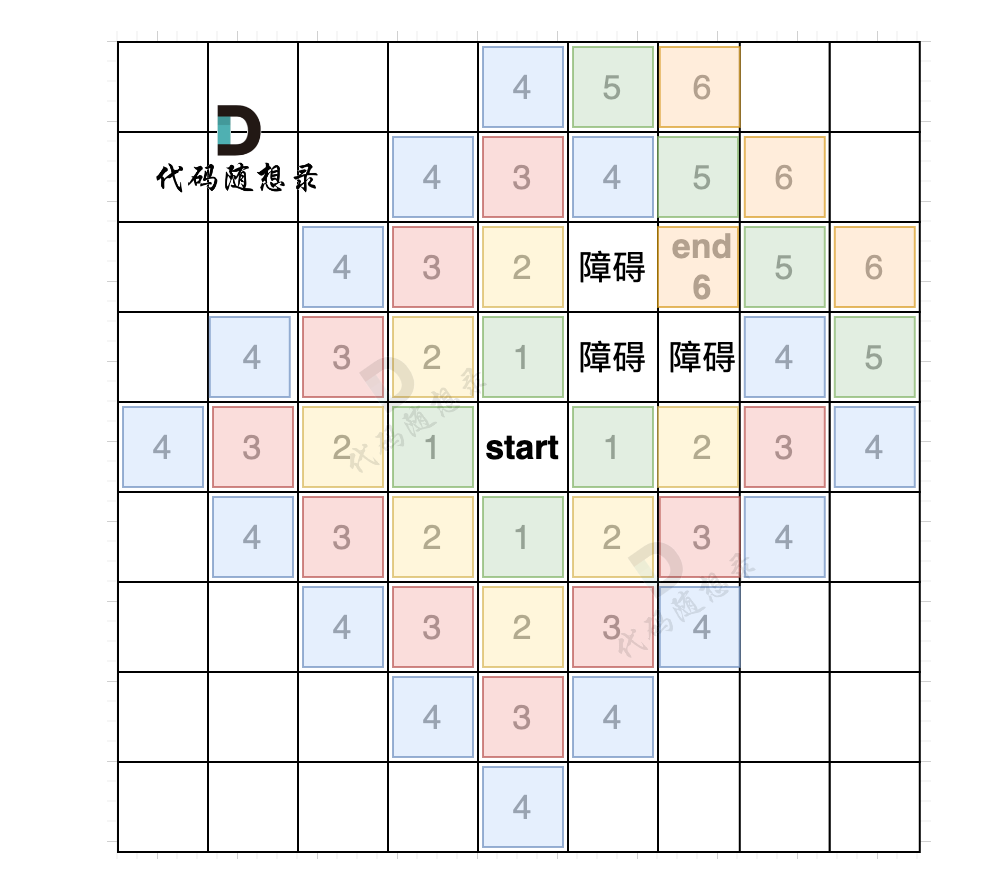
输入：grid = [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]
]
输出：3

思路

本题思路，遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。

在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。

那么如何把节点陆地所能遍历到的陆地都标记上呢，就可以使用 DFS，BFS或者并查集

DFS:

class Solution {boolean[][] visited;  //定义成全局的，不用传递int dir[][]={{0,1},{0,-1},{1,0},{-1,0}};  //右、左、下、上//把与某陆地结点相邻的陆地都标记上public void DFS(char[][] grid,int x,int y){   if(visited[x][y]==true||grid[x][y]=='0') //如果被访问过或者是水return;visited[x][y]=true;for(int i=0;i<4;i++){ //四个方向遍历一遍int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;//也可以把上面的放这里，if(visited[x][y]==false && grid[x][y]=='1')DFS(grid,nx,ny);}}public int numIslands(char[][] grid) {int count=0;visited=new boolean[grid.length][grid[0].length];//遇到一个没有遍历过的节点陆地，计数器就加一//然后把该节点陆地所能遍历到的陆地都标记上。for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(visited[i][j]==false && grid[i][j]=='1'){count++;DFS(grid,i,j);}}}return count;}
}

BFS

不少同学用广搜做这道题目的时候，超时了。 这里有一个广搜中很重要的细节：

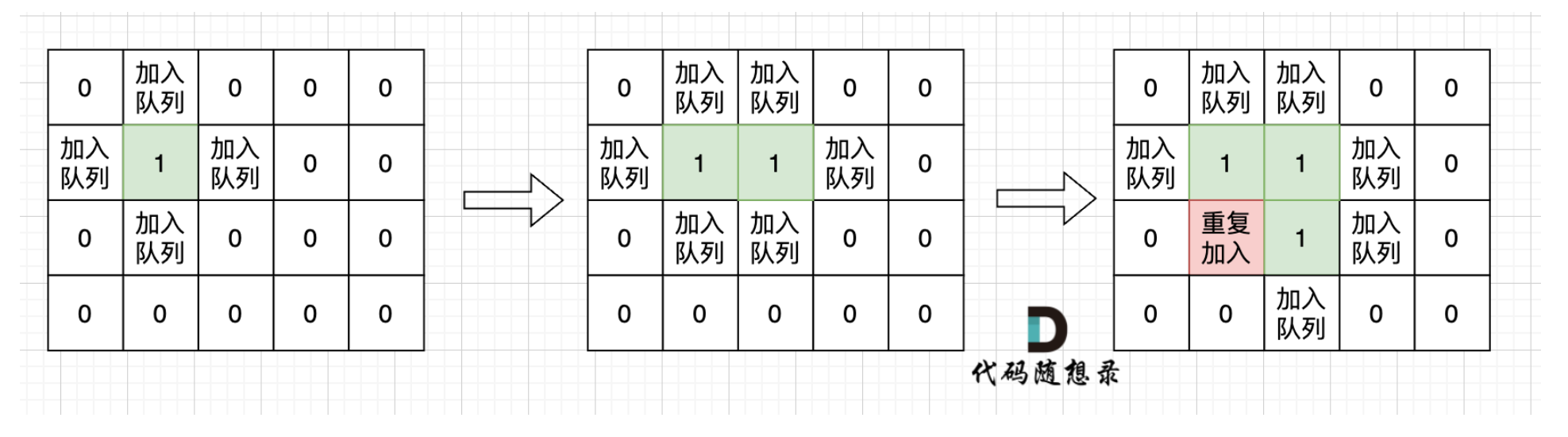
根本原因是只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过。

很多同学可能感觉这有区别吗？

如果从队列拿出节点，再去标记这个节点走过，就会发生下图所示的结果，会导致很多节点重复加入队列。

class Solution {boolean[][] visited;  //定义成全局的，不用传递int dir[][]={{0,1},{0,-1},{1,0},{-1,0}};  //右、左、下、上//把与某陆地结点相邻的陆地都标记上public void BFS(char[][] grid,int x,int y){   Deque<int[]> queue=new ArrayDeque<>();queue.offer(new int[]{x,y});visited[x][y]=true; //只要入队就标记while(!queue.isEmpty()){int[] cur=queue.poll();int cx=cur[0];int cy=cur[1];for(int i=0;i<4;i++){int nx=cx+dir[i][0];int ny=cy+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;if(visited[nx][ny]==false && grid[nx][ny]=='1'){   queue.offer(new int[]{nx,ny});visited[nx][ny]=true;}}}    }public int numIslands(char[][] grid) {int count=0;visited=new boolean[grid.length][grid[0].length];//遇到一个没有遍历过的节点陆地，计数器就加一//然后把该节点陆地所能遍历到的陆地都标记上。for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(visited[i][j]==false && grid[i][j]=='1'){count++;BFS(grid,i,j);}}}return count;}
}

695、岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

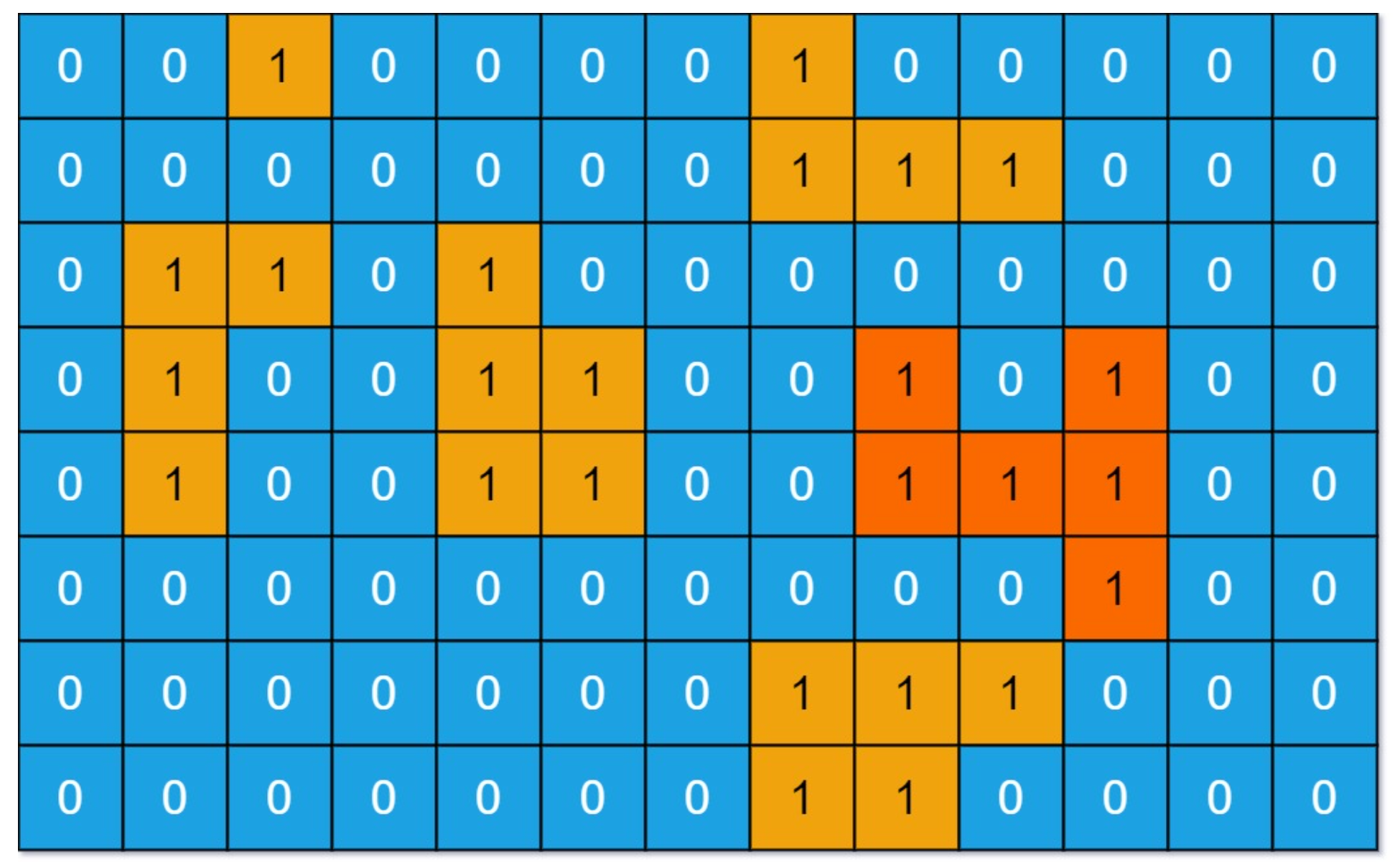
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

DFS:

设置一个全局变量count，每次DFS的时候++，遍历的时候把count置为0

class Solution {boolean[][] visited;int[][] dir ={{0,1},{0,-1},{1,0},{-1,0}};int count;public void DFS(int[][] grid,int x,int y){   if(visited[x][y]==true ||grid[x][y]==0)return;visited[x][y]=true;count++;for(int i=0;i<4;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;DFS(grid,nx,ny);}}public int maxAreaOfIsland(int[][] grid) {visited=new boolean[grid.length][grid[0].length];int result=0;  //记录最大值for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(visited[i][j]==false && grid[i][j]==1){count=0; //每次找的时候，赋值为0DFS(grid,i,j);result=Math.max(result,count);}}}return result;}
}

BFS

class Solution {boolean[][] visited;int[][] dir ={{0,1},{0,-1},{1,0},{-1,0}};int count;public void BFS(int[][] grid,int x,int y){   Deque<int[]> queue=new ArrayDeque<>();queue.offer(new int[]{x,y});visited[x][y]=true;count++;while(!queue.isEmpty()){int [] cur=queue.poll();int cx=cur[0];int cy=cur[1];for(int i=0;i<4;i++){int nx=cx+dir[i][0];int ny=cy+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;if(visited[nx][ny]==false && grid[nx][ny]==1){queue.offer(new int[]{nx,ny});visited[nx][ny]=true;count++;}}}     }public int maxAreaOfIsland(int[][] grid) {visited=new boolean[grid.length][grid[0].length];int result=0;  //记录最大值for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(visited[i][j]==false && grid[i][j]==1){count=0; //每次找的时候，赋值为0BFS(grid,i,j);result=Math.max(result,count);}}}return result;}
}

1020、飞地的数量

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

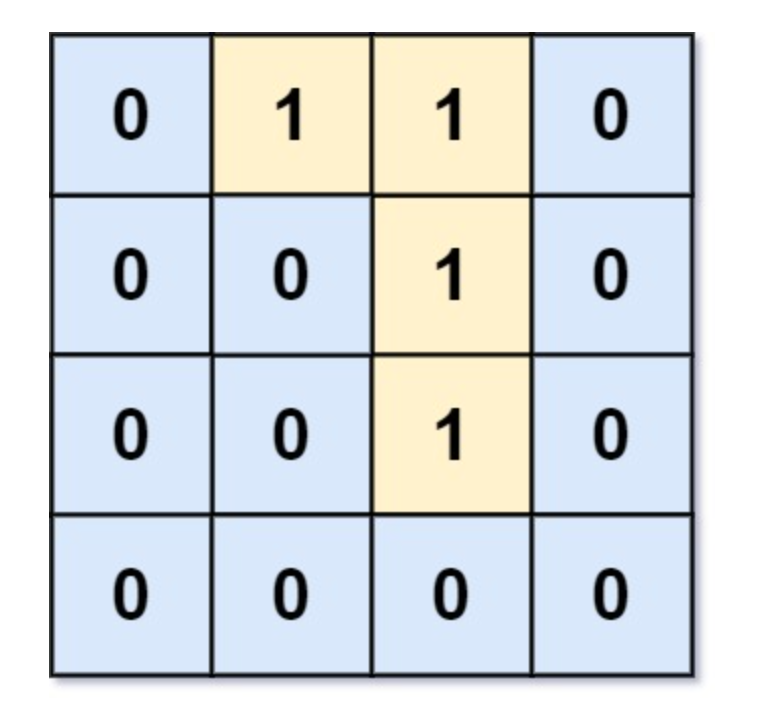
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

思路：

本题要求找到不靠边的陆地面积，那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋，然后再去重新遍历地图的时候，统计此时还剩下的陆地就可以了，所以不需要使用visited数组。

DFS：

class Solution {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};public void DFS(int[][] grid,int x,int y){if(grid[x][y]==0)return;grid[x][y]=0;   //访问一个陆地，就把他变成海洋for(int i=0;i<4;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;DFS(grid,nx,ny);}}public int numEnclaves(int[][] grid) {int count=0;//遍历边界，如果边界是陆地，就使用dfs把相邻的变成海洋for(int i=0;i<grid.length;i++){if(grid[i][0]==1)DFS(grid,i,0);if(grid[i][grid[0].length-1]==1)DFS(grid,i,grid[0].length-1);}for(int j=1;j<grid[0].length-1;j++){if(grid[0][j]==1)DFS(grid,0,j);if(grid[grid.length-1][j]==1)DFS(grid,grid.length-1,j);}//计算陆地单元格的数量for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(grid[i][j]==1)count++;}}return count;}
}

BFS：

class Solution {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};public void BFS(int[][] grid,int x,int y){Queue<int[]> queue =new LinkedList<>();queue.offer(new int[]{x,y});grid[x][y]=0;// 把陆地变为海洋while(!queue.isEmpty()){int[] cur=queue.poll();int cx=cur[0];int cy=cur[1];for(int i=0;i<4;i++){int nx=cx+dir[i][0];int ny=cy+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;if(grid[nx][ny]==1){queue.offer(new int[]{nx,ny});grid[nx][ny]=0;   // 把陆地变为海洋}} }}public int numEnclaves(int[][] grid) {int count=0;//遍历边界，如果边界是陆地，就使用dfs把相邻的变成海洋for(int i=0;i<grid.length;i++){if(grid[i][0]==1)BFS(grid,i,0);if(grid[i][grid[0].length-1]==1)BFS(grid,i,grid[0].length-1);}for(int j=1;j<grid[0].length-1;j++){if(grid[0][j]==1)BFS(grid,0,j);if(grid[grid.length-1][j]==1)BFS(grid,grid.length-1,j);}//计算陆地单元格的数量for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(grid[i][j]==1)count++;}}return count;}
}

130、被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

示例 1：

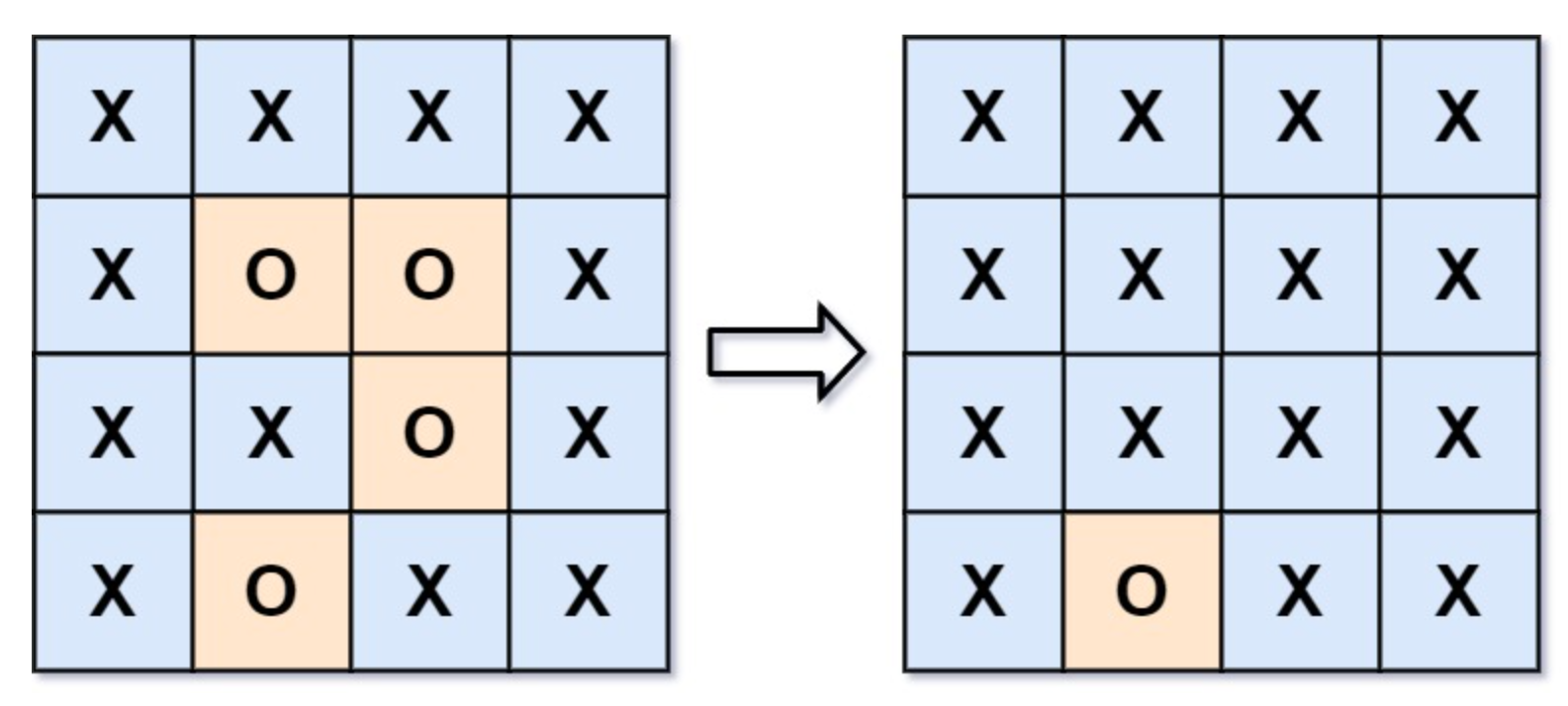
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

被围绕的区域就是出不去的区域。

与上一题的思路类似，任何边界上的O以及与边界O相邻的O都不会变动，其他的O都会被填充为X，因此先对边界进行遍历，把这些与边界O以及边界相邻的O都标记为A ，然后遍历整个数组，把O变为X，把A变为O

DFS：

class Solution {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};public void DFS(char[][] board,int x,int y){if(board[x][y]=='X'||board[x][y]=='A')return;//把边界O以及边界相邻的O标记为Aboard[x][y]='A';for(int i=0;i<4;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=board.length||ny>=board[0].length)continue;DFS(board,nx,ny);}}public void solve(char[][] board) {//对边界进行DFSfor(int i=0;i<board.length;i++){if(board[i][0]=='O')DFS(board,i,0);if(board[i][board[0].length-1]=='O')DFS(board,i,board[0].length-1);}for(int j=1;j<board[0].length-1;j++){if(board[0][j]=='O')DFS(board,0,j);if(board[board.length-1][j]=='O')DFS(board,board.length-1,j);}for(int i=0;i<board.length;i++){for(int j=0;j<board[0].length;j++){if(board[i][j]=='O')board[i][j]='X';if(board[i][j]=='A')   //注意这两个的if顺序不能颠倒board[i][j]='O';}}}
}

BFS：

class Solution {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};public void BFS(char[][] board,int x,int y){Queue<int[]> queue =new LinkedList<>();queue.offer(new int[]{x,y});//先把O转换成Aboard[x][y]='A';while(!queue.isEmpty()){int[] cur=queue.poll();int cx=cur[0];int cy=cur[1];for(int i=0;i<4;i++){int nx=cx+dir[i][0];int ny=cy+dir[i][1];if(nx<0||ny<0||nx>=board.length||ny>=board[0].length)continue;if(board[nx][ny]=='X' ||board[nx][ny]=='A')continue;queue.offer(new int[]{nx,ny});board[nx][ny]='A';   //把O入队并修改成A}}}public void solve(char[][] board) {//对边界进行BFSfor(int i=0;i<board.length;i++){if(board[i][0]=='O')BFS(board,i,0);if(board[i][board[0].length-1]=='O')BFS(board,i,board[0].length-1);}for(int j=1;j<board[0].length-1;j++){if(board[0][j]=='O')BFS(board,0,j);if(board[board.length-1][j]=='O')BFS(board,board.length-1,j);}for(int i=0;i<board.length;i++){for(int j=0;j<board[0].length;j++){if(board[i][j]=='O')board[i][j]='X';if(board[i][j]=='A')   //注意这两个的if顺序不能颠倒board[i][j]='O';}}}
}

417、太平洋大西洋水流问题

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

思路：与之前类似，本题只需要设置两个数组来分别记录能流入太平洋和流入大西洋的位置，然后就可以找到既可流向太平洋也可流向大西洋的位置，因为海洋是在周边，所以还是要从周边进行遍历。标记能流入到周边的

DFS：

class Solution {int[][] dir ={{0,1},{0,-1},{1,0},{-1,0}};//使用DFS来找到能到达海洋的位置public void DFS(int[][] heights,boolean[][] mark,int x,int y){if(mark[x][y]==true)return;mark[x][y]=true;for(int i=0;i<4;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=heights.length||ny>=heights[0].length)continue;if(heights[x][y]>heights[nx][ny])  //能流入到周边的continue;DFS(heights,mark,nx,ny);	}}public List<List<Integer>> pacificAtlantic(int[][] heights) {List<List<Integer>> ans =new ArrayList<>();int m=heights.length;int n=heights[0].length;boolean[][] pacific=new boolean[m][n];    //标记能流入太平洋的位置boolean[][] atlantic=new boolean[m][n];   //标记能流入大西洋的位置for(int i=0;i<m;i++){DFS(heights,pacific,i,0); //遍历最左列DFS(heights,atlantic,i,n-1);  //遍历最右列}for(int j=0;j<n;j++)//这个循环要从0开始，因为和大西洋也是相邻的{DFS(heights,pacific,0,j);   //最上列DFS(heights,atlantic,m-1,j); //最下列}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(pacific[i][j]==true && atlantic[i][j]==true)ans.add(List.of(i,j));}}return ans;}
}

BFS:

class Solution {int[][] dir ={{0,1},{0,-1},{1,0},{-1,0}};//使用BFS来找到能到达海洋的位置public void BFS(int[][] heights,boolean[][] mark,int x,int y){Queue<int[]> queue =new LinkedList<>();queue.offer(new int[]{x,y});mark[x][y]=true;while(!queue.isEmpty()){int[] cur=queue.poll();int cx=cur[0];int cy=cur[1];for(int i=0;i<4;i++){int nx=cx+dir[i][0];int ny=cy+dir[i][1];if(nx<0||ny<0||nx>=heights.length||ny>=heights[0].length)continue;//高度不合适或者被访问过了//一定要加mark[nx][ny]==true，否则会死循环if(heights[cx][cy]>heights[nx][ny] ||mark[nx][ny]==true)continue;queue.offer(new int[]{nx,ny});  //能够到达海洋mark[nx][ny]=true;}}}public List<List<Integer>> pacificAtlantic(int[][] heights) {List<List<Integer>> ans =new ArrayList<>();int m=heights.length;int n=heights[0].length;boolean[][] pacific=new boolean[m][n];    //标记能流入太平洋的位置boolean[][] atlantic=new boolean[m][n];   //标记能流入大西洋的位置for(int i=0;i<m;i++){//可以共用一个队列，因为执行完一个BFS后，队列就空了BFS(heights,pacific,i,0); //遍历最左列BFS(heights,atlantic,i,n-1);  //遍历最右列}for(int j=0;j<n;j++)//这个循环要从0开始，因为和大西洋也是相邻的{BFS(heights,pacific,0,j);   //最上列BFS(heights,atlantic,m-1,j); //最下列}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(pacific[i][j]==true && atlantic[i][j]==true)ans.add(List.of(i,j));}}return ans;}
}

827、最大人工岛

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的 1 形成。

示例 1:

输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:

输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。

暴力思路：

遍历地图尝试 将每一个 0 改成1，然后去使用DFS或者BFS搜索地图中的最大的岛屿面积，整体时间复杂度为：n^4。

优化思路：

其实每次深搜遍历计算最大岛屿面积，我们都做了很多重复的工作。

只要用一次深搜把每个岛屿的面积记录下来就好。

第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积

第二步：在遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。

拿如下地图的岛屿情况来举例： （1为陆地）

第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示：

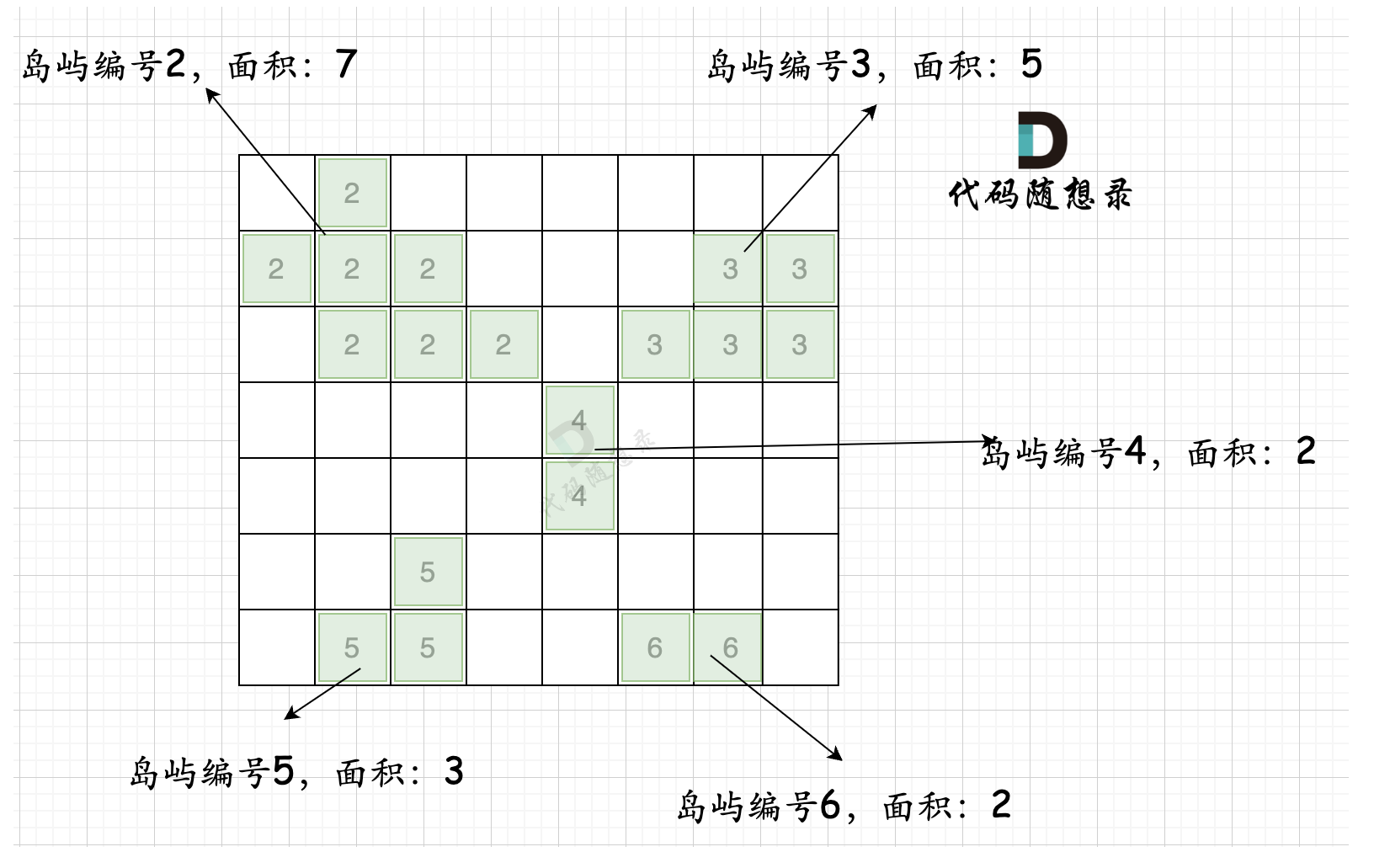
本过程代码如下：

class Solution {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};int count=0;boolean[][] visited;  //访问数组//使用DFS把相邻的陆地都标记成一样的数字public void DFS(int[][] grid,int x,int y,int mark){if(visited[x][y]||grid[x][y]==0)return;visited[x][y]=true; //标记访问过grid[x][y]=mark;   //给陆地添加新标记count++;for(int i=0;i<4;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;DFS(grid,nx,ny,mark);}}public int largestIsland(int[][] grid) {int n=grid.length;int m=grid[0].length;visited=new boolean[n][m];int[] gridNum=new int[n*m]; //记录每一个岛屿的面积int mark=2;boolean isAllGrid = true; // 标记是否整个地图都是陆地for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==0) isAllGrid=false;if(grid[i][j]==1 &&visited[i][j]==false){count=0;   //每次DFS之前把count清空DFS(grid,i,j,mark);  //使用DFS把相邻的陆地都标记成一样的数字gridNum[mark]=count;mark++;}}}}
}

这个过程的时间复杂度是n²，因为n * n这个方格地图中，每个节点我们就遍历一次，并不会重复遍历。

第二步过程如图所示：

也就是遍历每一个0的方格，并统计其相邻岛屿面积，最后取一个最大值。这个过程的时间复杂度也为 n²。

所以整个代码的复杂度就是n²

class Solution {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};int count=0;boolean[][] visited;  //访问数组//使用DFS把相邻的陆地都标记成一样的数字public void DFS(int[][] grid,int x,int y,int mark){if(visited[x][y]||grid[x][y]==0)return;visited[x][y]=true; //标记访问过grid[x][y]=mark;   //给陆地添加新标记count++;for(int i=0;i<4;i++){int nx=x+dir[i][0];int ny=y+dir[i][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;DFS(grid,nx,ny,mark);}}public int largestIsland(int[][] grid) {int n=grid.length;int m=grid[0].length;visited=new boolean[n][m];int[] gridNum=new int[n*m+2]; //记录每一个岛屿的面积,加2是防止矩阵只有1的长度int mark=2;boolean isAllGrid = true; // 标记是否整个地图都是陆地//把相连的岛屿进行标记for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==0) isAllGrid=false;if(grid[i][j]==1 &&visited[i][j]==false){count=0;   //每次DFS之前把count清空DFS(grid,i,j,mark);  //使用DFS把相邻的陆地都标记成一样的数字gridNum[mark]=count;mark++;}}}//把一个0变为陆地，并计算最大的面积if(isAllGrid)return n*m;int result=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==0)   //把0换成1{int num=1;   //0本身的面积boolean[] visitedGrid =new boolean[mark]; //每次变过之后，标记0周边访问过的岛屿，有可能相邻的是属于同一个岛屿for(int k=0;k<4;k++){int nx=i+dir[k][0];int ny=j+dir[k][1];if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length)continue;if(visitedGrid[grid[nx][ny]]==true)continue;num+=gridNum[grid[nx][ny]];  // 把相邻四面的岛屿数量加起来visitedGrid[grid[nx][ny]]=true;  // 标记该岛屿已经添加过}result=Math.max(result,num);}}}return result;}
}

把问题转换为图的遍历

127、单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk：

• 每一对相邻的单词只差一个字母。
• 对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
• sk == endWord

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回 从 beginWord 到 endWord 的 最短转换序列 中的 __单词数目 。如果不存在这样的转换序列，返回 0 。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

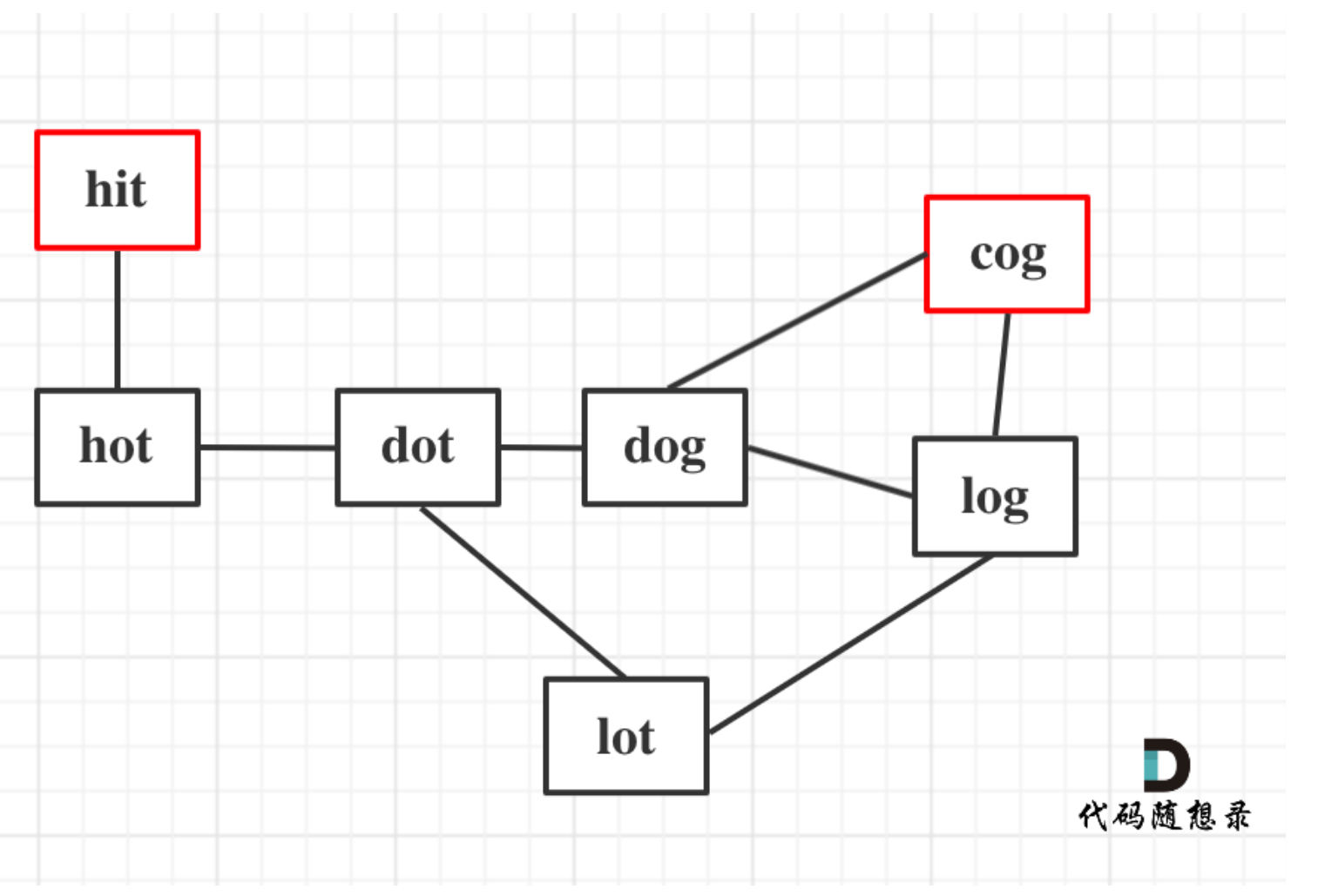
这道题要解决两个问题：

• 图中的线是如何连在一起的
• 起点和终点的最短路径长度

首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个，所以判断点与点之间的关系，要自己判断是不是差一个字符，如果差一个字符，那就是有链接。

然后就是求起点和终点的最短路径长度，这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。

另外需要有一个注意点：

• 本题是一个无向图，需要用标记位，标记着节点是否走过，否则就会死循环！
• 本题给出集合是数组型的，可以转成set结构，查找更快一些

转换为图求最短路径

使用一个队列记录bfs的结点，并使用一个map记录访问过的结点和路径长度，使用Hashset判断更换后的单词是否在列表中。

class Solution {public int ladderLength(String beginWord, String endWord, List<String> wordList) {HashSet<String> wordset =new HashSet<>(wordList); //加快判断速度if(wordset.size()==0 ||!wordset.contains(endWord))return 0;Queue<String> queue =new LinkedList<>();queue.offer(beginWord);//记录单词对应的路径长度，同时也有标记功能，标记wordList的访问过的单词Map<String,Integer> map =new HashMap<>(); map.put(beginWord,1);while(!queue.isEmpty()){String word=queue.poll(); //从队列中取出第一个单词int path=map.get(word);   //单词对应的路径长度for(int i=0;i<word.length();i++)   //遍历单词每个字符，把单词进行替换{char[] chars=word.toCharArray(); //变为数组，方便操作for(char k='a';k<='z';k++){chars[i]=k;String newword=String.valueOf(chars); //替换成新单词if(endWord.equals(newword))return path+1;//如果新单词在列表中，并且没有访问过if(wordset.contains(newword) && !map.containsKey(newword)){queue.offer(newword); //加入队列map.put(newword,path+1); //记录单词对应的路径长度}}}} return 0;//未找到}
}

841、钥匙和房间

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。

当你进入一个房间，你可能会在里面找到一套不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。

给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true，否则返回 false。

示例 1：

输入：rooms = [[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。

示例 2：

输入：rooms = [[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。

相当于一个有向图，rooms[i] 就是i结点能到达的结点。能到达就标记，然后看最后能否标记完

DFS

class Solution {boolean[] visited;//DFS的第一种写法，处理当前访问的结点public void DFS(List<List<Integer>> rooms,int curKey){if(visited[curKey])return;visited[curKey]=true;for(int key:rooms.get(curKey)){DFS(rooms,key);}}//DFS的第二种写法,处理下一个结点public void DFS(List<List<Integer>> rooms,int curKey){//这里 没有终止条件，而是在 处理下一层节点的时候来判断for(int key:rooms.get(curKey)){if (visited[key] == false) { // 处理下一层节点，判断是否要进行递归{   visited[key] = true;DFS(rooms,key);}}}public boolean canVisitAllRooms(List<List<Integer>> rooms) {visited=new boolean[rooms.size()]; //标记数组DFS(rooms,0);for(int i=0;i<visited.length;i++){if(visited[i]==false)return false;}return true;}}

什么本题就没有回溯呢？

代码中可以看到dfs函数下面并没有回溯的操作。

此时就要在思考本题的要求了，本题是需要判断 0节点是否能到所有节点，那么我们就没有必要回溯去撤销操作了，只要遍历过的节点一律都标记上。

那什么时候需要回溯操作呢？

当我们需要搜索一条可行路径的时候，就需要回溯操作了，因为没有回溯，就没法“调头”

BFS

class Solution {//因为只需要遍历一次BFS 所以可以写在主函数里public boolean canVisitAllRooms(List<List<Integer>> rooms) {boolean[] visited=new boolean[rooms.size()]; //标记数组Queue<Integer> queue =new LinkedList<>();queue.add(0);visited[0]=true;while(!queue.isEmpty()){int curKey=queue.poll();for(int key:rooms.get(curKey)){if(visited[key]==false){queue.add(key);visited[key]=true;}}}for(int i=0;i<visited.length;i++){if(visited[i]==false)return false;}return true;}
}

463、岛屿的周长

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

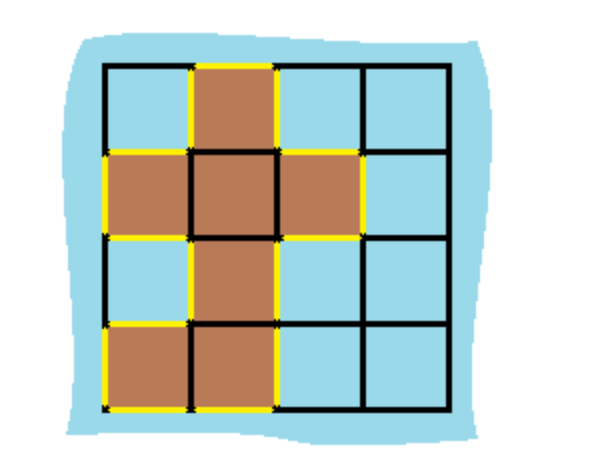
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

思路：

岛屿问题最容易让人想到BFS或者DFS，但是这道题还真的没有必要，别把简单问题搞复杂了

遍历每一个空格，遇到岛屿，计算其上下左右的情况，遇到水域或者出界的情况，就可以计算边了

class Solution {public int islandPerimeter(int[][] grid) {int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};int count=0;for(int i=0;i<grid.length;i++){for(int j=0;j<grid[0].length;j++){if(grid[i][j]==1)  //遇到陆地{for(int k=0;k<4;k++){int nx=i+dir[k][0];int ny=j+dir[k][1];//新位置遇到边界,不要忘记continue，因为下面会利用到这些坐标if(nx<0||ny<0||nx>=grid.length||ny>=grid[0].length){count++;continue;}if(grid[nx][ny]==0)  //x新位置遇到水域，周长加1count++;}}}}return count;}
}