双曲函数(Hyperbolic functuons)公式
在python等语言里有双曲函数库和反双曲函数库,但是并没有包含所有的双曲函数。以numpy为例子,numpy只提供了sinh、cosh、tanh、arcsinh、arccosh、arctanh六种函数,那么其余的就需要用公式计算了。
转换公式
对于函数库不能直接计算的,我整理出了计算公式:
coth x = 1 tanh x s e c h x = 1 cosh x c s c h x = 1 sinh x a r c c o t h x = a r c t a n ( 1 x ) a r c s e c h x = a r c c o s ( 1 x ) a r c c s c h x = a r c s e c ( 1 x ) \coth x = \frac1{\tanh x} \\ sech\thinspace x = \frac1{\cosh x} \\ csch\thinspace x = \frac1{\sinh x} \\ arccoth\thinspace x = arctan (\frac1x)\\ arcsech\thinspace x = arccos (\frac1x)\\ arccsch\thinspace x = arcsec(\frac1x) cothx=tanhx1sechx=coshx1cschx=sinhx1arccothx=arctan(x1)arcsechx=arccos(x1)arccschx=arcsec(x1)
导数公式
对双曲函数和反双曲函数求导的公式也非常重要,必须要背诵下来。
d d x ( sinh x ) = cosh x d d x ( cosh x ) = sinh x d d x ( tanh x ) = s e c h 2 x d d x ( coth x ) = − c s c h 2 x d d x ( s e c h x ) = − s e c h x t a n h x d d x ( c s c h x ) = − c s c h x c o t h x \frac{d}{dx}(\sinh x)=\cosh x\\ \frac{d}{dx}(\cosh x)=\sinh x\\ \frac{d}{dx}(\tanh x)=sech^2\thinspace x\\ \frac{d}{dx}(\coth x)=-csch^2\thinspace x\\ \frac{d}{dx}(sech x)= -sech\thinspace x \thinspace tanh\thinspace x\\ \frac{d}{dx}(csch x)= -csch\thinspace x \thinspace cot h\thinspace x\\ dxd(sinhx)=coshxdxd(coshx)=sinhxdxd(tanhx)=sech2xdxd(cothx)=−csch2xdxd(sechx)=−sechxtanhxdxd(cschx)=−cschxcothx
接下来是反双曲函数inverse hyperbolic functions的导数公式:
d d x ( a r c s i n h x ) = 1 x 2 + 1 d d x ( a r c c o s h x ) = 1 x 2 − 1 , x > 1 d d x ( a r c t a n h x ) = 1 1 − x 2 d d x ( a r c c o t h x ) = 1 1 − x 2 d d x ( a r c s e c h x ) = − 1 x 1 − x 2 d d x ( a r c c o s h x ) = − 1 ∣ x ∣ 1 + x 2 \frac{d}{dx}(arcsinh \thinspace x)=\frac1{\sqrt{x^2+1}}\\ \frac{d}{dx}(arccosh \thinspace x)=\frac1{\sqrt{x^2-1}},x > 1\\ \frac{d}{dx}(arctanh \thinspace x)=\frac1{{1-x^2}}\\ \frac{d}{dx}(arccoth \thinspace x)=\frac1{{1-x^2}}\\ \frac{d}{dx}(arcsech \thinspace x)=-\frac1{x\sqrt{1-x^2}}\\ \frac{d}{dx}(arccosh \thinspace x)=-\frac1{|x|\sqrt{1+x^2}}\\ dxd(arcsinhx)=x2+11dxd(arccoshx)=x2−11,x>1dxd(arctanhx)=1−x21dxd(arccothx)=1−x21dxd(arcsechx)=−x1−x21dxd(arccoshx)=−∣x∣1+x21
积分公式
上面这些求导公式,反推一下就是积分公式了,但是有些特殊的积分公式,不能直接推导出来,需要记忆:
∫ d x a 2 + x 2 = a r c s i n h ( x a ) + C , a > 0 ∫ d x x 2 − a 2 = a r c c o s h ( x a ) + C , x > a > 0 ∫ d x a 2 − x 2 = { 1 a a r c t a n h ( x a ) + C , x 2 < a 2 1 a a r c c o t h ( x a ) + C , x 2 > a 2 ∫ d x x a 2 − x 2 = − 1 a a r c s e c h ( x a ) + C , 0 < x < a ∫ d x x a 2 + x 2 = − 1 a a r c c s c h ∣ x a ∣ + C , x ≠ 0 , a > 0 \int\frac{dx}{\sqrt{a^2+x^2}}= arcsinh \thinspace (\frac{x}{a})+C,a>0\\ \int\frac{dx}{\sqrt{x^2-a^2}}= arccosh \thinspace (\frac{x}{a})+C,x>a>0\\ \int\frac{dx}{a^2-x^2}= \begin{cases} \frac1a \thinspace arctanh \thinspace (\frac{x}{a})+C,x^2<a^2\\ \frac1a \thinspace arccoth \thinspace (\frac{x}{a})+C,x^2>a^2\\ \end{cases}\\ \int\frac{dx}{x\sqrt{a^2-x^2}}=-\frac1a arcsech \thinspace (\frac{x}{a})+C,0<x<a\\ \int\frac{dx}{x\sqrt{a^2+x^2}}=-\frac1a arccsch \thinspace \lvert \frac{x}{a}\rvert+C,x \neq 0, a>0 ∫a2+x2dx=arcsinh(ax)+C,a>0∫x2−a2dx=arccosh(ax)+C,x>a>0∫a2−x2dx={a1arctanh(ax)+C,x2<a2a1arccoth(ax)+C,x2>a2∫xa2−x2dx=−a1arcsech(ax)+C,0<x<a∫xa2+x2dx=−a1arccsch∣ax∣+C,x=0,a>0
恒等式
最后,我再整理一点恒等式:
c o s h 2 x − s i n h 2 x = 1 s i n h x = 2 s i n h x c o s h x c o s h x = s i n h 2 x + c o s h 2 x c o s h 2 x = c o s h 2 x + 1 2 s i n h 2 x = c o s h 2 x − 1 2 t a n h 2 x = 1 − s e c h 2 x c o t h 2 x = 1 + c s c h 2 x cosh^2 \thinspace x -sinh^2 \thinspace x = 1\\ sinh\thinspace x = 2sinh\thinspace x \thinspace cosh\thinspace x \\ cosh\thinspace x = sinh^2\thinspace x \thinspace + cosh^2\thinspace x \\ cosh^2\thinspace x = \frac{cosh\thinspace 2x +1}2\\ sinh^2\thinspace x = \frac{cosh\thinspace 2x -1}2\\ tanh^2\thinspace x = 1-sech^2x\\ coth^2\thinspace x = 1+csch^2x\\ cosh2x−sinh2x=1sinhx=2sinhxcoshxcoshx=sinh2x+cosh2xcosh2x=2cosh2x+1sinh2x=2cosh2x−1tanh2x=1−sech2xcoth2x=1+csch2x
相关文章:
公式)
双曲函数(Hyperbolic functuons)公式
在python等语言里有双曲函数库和反双曲函数库,但是并没有包含所有的双曲函数。以numpy为例子,numpy只提供了sinh、cosh、tanh、arcsinh、arccosh、arctanh六种函数,那么其余的就需要用公式计算了。 转换公式 对于函数库不能直接计算的&#…...

【CSS/SCSS】@layer的介绍及使用方法
目录 基本用法layer 的作用与优点分离样式职责,增强代码可读性和可维护性防止无意的样式冲突精确控制样式的逐层覆盖提高复用性 兼容性实际示例:使用 import 管理加载顺序实际示例:混入与 layer 结合使用 layer 是 CSS 中用于组织和管理样式优…...

我为什么投身于青少年AI编程?——打造生态圈(三)
第五部分 青少年AI编程生态圈 一、生态圈 主要涵盖家庭、社区/中小学、高校高职、主管部门。 1、家庭 我们与社区/中小学一道打造让家长满意的模式。 教得好: 费用少: 家门口: 2、社区/中小学 社区党群服务中心和中小学都有大面积科普…...

出海要深潜,中国手机闯关全球化有了新标杆
经济全球化的大势之下,中国科技企业开拓海外市场已成为一种必然选择。 对于国内手机企业来说,推进全球商业版图扩张,业务潜力巨大,海外市场是今后的关键增长引擎。 当前中国手机厂商在海外市场的发展,有收获也有坎坷…...

百度SEO中的关键词密度与内容优化研究【百度SEO专家】
大家好,我是百度SEO专家(林汉文),在百度SEO优化中,关键词密度和关键词内容的优化对提升页面排名至关重要。关键词的合理布局与内容的质量是确保网页在百度搜索结果中脱颖而出的关键因素。下面我们将从关键词密度和关键…...

如何用fastapi集成pdf.js 的viewer.html ,并支持 mjs
fastapi 框架 集成pdf.js 的 viewer.html?file=***,支持跨域,支持.mjs .wasm .pdf 给出完整示例代码 要在 FastAPI 框架中集成 pdf.js 的 viewer.html,并支持跨域访问以及 .mjs、.wasm、.pdf 文件的正确加载,可以按照以下步骤进行。下面提供一个完整的示例,包括项目结构…...

文件相对路径与绝对路径
前言: 在写代码绘制图像的过程中,发现出现cant read input file的异常,而且输出框没有绘制图片,所以寻找解决方案。先贴上之前写的简洁版绘制图像代码 1.BackGround类 import java.awt.image.BufferedImage;public class BackG…...

Linux 重启命令全解析:深入理解与应用指南
Linux 重启命令全解析:深入理解与应用指南 在 Linux 系统中,掌握正确的重启命令是确保系统稳定运行和进行必要维护的关键技能。本文将深入解析 Linux 中常见的重启命令,包括功能、用法、适用场景及注意事项。 一、reboot 命令 功能简介 re…...

【北京迅为】《STM32MP157开发板嵌入式开发指南》-第六十七章 Trusted Firmware-A 移植
iTOP-STM32MP157开发板采用ST推出的双核cortex-A7单核cortex-M4异构处理器,既可用Linux、又可以用于STM32单片机开发。开发板采用核心板底板结构,主频650M、1G内存、8G存储,核心板采用工业级板对板连接器,高可靠,牢固耐…...

`a = a + b` 与 `a += b` 的区别
在 Java 中,a a b 和 a b 都用于将 b 的值加到 a 上,但它们之间存在一些重要的区别,尤其是在类型转换和操作行为方面。 使用 操作符时,Java 会自动进行隐式类型转换,而使用 则不会。这意味着在 a b 的情况下&am…...

mysqld.log文件过大,清理后不改变所属用户
#1024程序员节# 一、背景 突然有一天,我的mysql报磁盘不足了。仔细查看才发现,是磁盘满了。而MySQL的日志文件占用了91个G.如下所示: [roothost-172-16-14-128 mysql]# ls -lrth 总用量 93G -rw-r----- 1 mysql mysql 1.1G 7月 30 2023 m…...
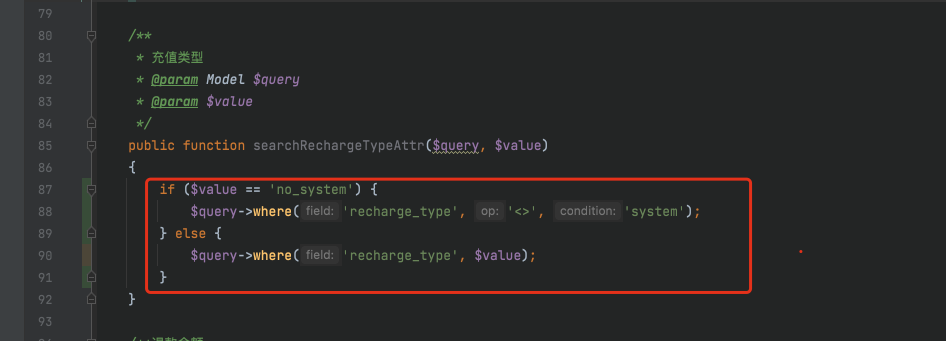
v4.7+版本用户充值在交易统计中计算双倍的问题修复
app/services/statistic/TradeStatisticServices.php 文件中 $whereInRecharge[recharge_type] no_system; $whereInRecharge[recharge_type] system; app/model/user/UserRecharge.php 中 修改此搜索器内容 public function searchRechargeTypeAttr($query, $value){ if…...

[GXYCTF 2019]Ping Ping Ping 题解(多种解题方式)
知识点: 命令执行 linux空格绕过 反引号绕过 变量绕过 base64编码绕过 打开页面提示 "听说php可以执行系统函数?我来康康" 然后输入框内提示输入 bjut.edu.cn 输入之后回显信息,是ping 这个网址的信息 输入127.0.0.1 因为提示是命令…...

MODSI EVI 数据的时间序列拟合一阶谐波模型
目录 简介 函数 ee.Reducer.linearRegression(numX, numY) Arguments: Returns: Reducer ee.Image.cat(var_args) Arguments: Returns: Image hsvToRgb() Arguments: Returns: Image 代码 结果 简介 MODIS/006/MOD13A1数据是由美国国家航空航天局(NASA)的MODIS…...

Java:String类(超详解!)
一.常用方法 🥏1.字符串构造 字符串构造有三种方法: 📌注意: 1. String是引用类型,内部并不存储字符串本身 如果String是一个引用那么s1和s3应该指向同一个内容,s1和s2是相等的,应该输出两…...

【日志】力扣13.罗马数字转整数 || 解决泛型单例热加载失败问题
2024.10.28 【力扣刷题】 13. 罗马数字转整数 - 力扣(LeetCode)https://leetcode.cn/problems/roman-to-integer/description/?envTypestudy-plan-v2&envIdtop-interview-150这题用模拟的思想可以给相应的字母赋值,官方的答案用的是用一…...

Mybatis高级
系列文章目录 高级Mybatis,一些结果映射,引入新的注解 目录 系列文章目录 文章目录 一、结果映射 1.ResultType 2.ResultMap 基础应用: 二、一对一 嵌套结果和嵌套查询 嵌套结果 嵌套查询 区别 三、一对多 四、多对多 五、注解补充 1.一对一…...

【spark】spark structrued streaming读写kafka 使用kerberos认证
spark版本:2.4.0 官网 Spark --files使用总结 Spark --files理解 一、编写jar import org.apache.kafka.clients.CommonClientConfigs import org.apache.kafka.common.config.SaslConfigs import org.apache.spark.sql.SparkSession import org.apache.spark.sql.streaming.T…...

【脚本】B站视频AB复读
控制台输入如下代码,回车 const video document.getElementsByTagName("video")[0];//获取bpx-player-control-bottom-center容器,更改其布局方式const div document.getElementsByClassName("bpx-player-control-bottom-center")[0];div.sty…...
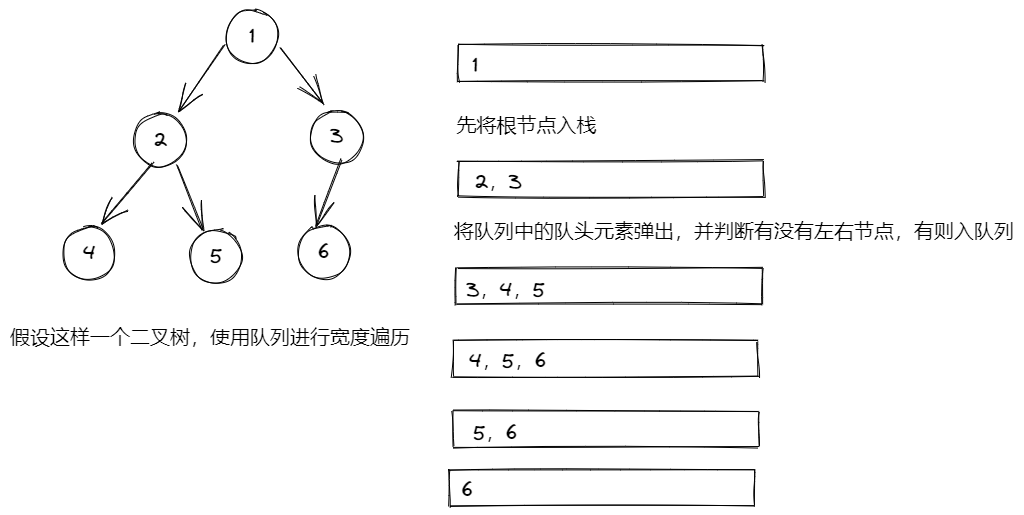
leetcode - 257. 二叉树的所有路径
257. 二叉树的所有路径 题目 解决 做法一:深度优先搜索 回溯 深度优先搜索(Depth-First Search, DFS)是一种用于遍历或搜索树或图的算法。这种搜索方式会尽可能深地探索每个分支,直到无法继续深入为止,然后回溯到上…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
