python机器人编程——一种3D骨架动画逆解算法的启示（上）

一、前言

我们用blender等3D动画软件时，会用到骨骼的动画，通过逆向IK动力学，可以实现控制少量点，就能控制一个复杂的骨架运动。这种IK动力学几乎是实时的，非常的高效。这种IK动力学算法的代表是fabrik 算法，该算法应被用于UE虚幻引擎、Unity等3D软件中。大至效果是，可以实现骨架的目标跟随，而且几乎是“实时”的：

这种感觉，不就是机械臂的虚拟拖拽吗？是否可以给机械臂的逆解，或者是虚拟化示教带来一些启发，是一个有意思的应用。本篇先来初步研究一下fabrik 算法。

二、fabrik 算法

该算法在文章 FABRIK: A fast, iterative solver for the Inverse Kinematics problem中有详细说明，FABRIK算法是一种用于解决逆运动学问题的启发式方法。它通过迭代地调整关节链，使末端执行器逐渐接近目标位置。与传统方法相比，FABRIK算法不需要使用旋转角度或矩阵，而是通过在线段上定位点来找到每个关节的位置，这使得它在计算上更加高效，并且能够产生视觉上现实的关节姿势。

三、python实现

网上已经有很多实现的python算法，这里，主要是利用实现的3D算法，实现在matplot中的IK，即，任意点击3D坐标点，实现IK，骨架的末端移动到目标点，就像开始的blender一样。

首先，我们需要导入一些必要的Python库，包括NumPy、Math、Matplotlib等，用于数学运算和图形绘制。

import numpy as np
import math
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import re

单位向量函数
定义了一个函数 unitVector，它接受一个向量作为输入，并返回该向量的单位向量。

def unitVector(vector):return vector / np.linalg.norm(vector)

Segment3D 类用于存储逆运动学链的一部分。它接受参考点坐标、段长度和初始角度作为参数，并计算出该段的新坐标。

class Segment3D:def __init__(self, referenceX, referenceY, referenceZ, length, zAngle, yAngle):self.zAngle = zAngleself.yAngle = yAngleself.length = lengthdeltaX = math.cos(math.radians(zAngle)) * lengthdeltaY = math.sin(math.radians(zAngle)) * lengthdeltaZ = math.sin(math.radians(yAngle)) * lengthnewX = referenceX + deltaXnewY = referenceY + deltaYnewZ = referenceZ + deltaZself.point = np.array([newX, newY, newZ])

FabrikSolver3D 类是FABRIK算法的核心，它初始化了一个3D逆运动学求解器，并提供了添加段、检查可达性、迭代求解和绘图等功能。

        
class FabrikSolver3D:""" An inverse kinematics solver in 3D. Uses the Fabrik Algorithm."""def __init__(self, baseX=0, baseY=0, baseZ=0,  marginOfError=0.01):# Create the base of the chain.self.basePoint = np.array([baseX, baseY, baseZ])# Initialize empty segment array -> [].self.segments = []# Initialize length of the chain -> 0.self.armLength = 0# Initialize the margin of error.self.marginOfError = marginOfErrorself.targetpoint=Noneself.fig = plt.figure()self.ax1 = self.fig.add_subplot(111, projection="3d")self.mousep=Nonedef addSegment(self, length, zAngle, yAngle):if len(self.segments) > 0:segment = Segment3D(self.segments[-1].point[0], self.segments[-1].point[1], self.segments[-1].point[2], length, zAngle + self.segments[-1].zAngle, self.segments[-1].yAngle + yAngle)else:# Maak een segment van de vector beginpoint, lengte en hoek.segment = Segment3D(self.basePoint[0], self.basePoint[1], self.basePoint[2], length, zAngle, yAngle)# Voeg lengte toe aan de totale armlengte.self.armLength += segment.length# Voeg de nieuwe segment toe aan de list.self.segments.append(segment)def isReachable(self, targetX, targetY, targetZ):if np.linalg.norm(self.basePoint - np.array([targetX, targetY, targetZ])) < self.armLength:return Truereturn Falsedef inMarginOfError(self, targetX, targetY, targetZ):if np.linalg.norm(self.segments[-1].point - np.array([targetX, targetY, targetZ])) < self.marginOfError:return Truereturn False     def iterate(self, targetX, targetY, targetZ):target = np.array([targetX, targetY, targetZ])# Backwards.for i in range(len(self.segments) - 1, 0, -1):if i == len(self.segments) - 1:self.segments[i-1].point = (unitVector(self.segments[i-1].point - target) * self.segments[i].length) + targetelse:self.segments[i-1].point = (unitVector(self.segments[i-1].point - self.segments[i].point) * self.segments[i].length) + self.segments[i].point# Forwards.for i in range(len(self.segments)):if i == 0:self.segments[i].point = (unitVector(self.segments[i].point - self.basePoint) * self.segments[i].length) + self.basePointelif i == len(self.segments) - 1:self.segments[i].point = (unitVector(self.segments[i-1].point - target) * self.segments[i].length * -1) + self.segments[i-1].pointelse:self.segments[i].point = (unitVector(self.segments[i].point - self.segments[i-1].point) * self.segments[i].length) + self.segments[i-1].pointdef compute(self, targetX, targetY, targetZ):if self.isReachable(targetX, targetY, targetZ):while not self.inMarginOfError(targetX, targetY, targetZ):self.iterate(targetX, targetY, targetZ)   self.targetpoint=[targetX, targetY, targetZ]else:print('Target not reachable.')sys.exit()def plot(self, save=False, name="graph"):self.ax1.clear()  # 清除当前轴ax1=self.ax1# Plot arm.for i, segment in enumerate(self.segments):#ax1.scatter(segment.point[2], segment.point[0], segment.point[1], c='b')ax1.scatter(segment.point[0], segment.point[1], segment.point[2], c='b')if i > 0:  # Connect to the previous segmentax1.plot([self.segments[i-1].point[0], segment.point[0]],[self.segments[i-1].point[1], segment.point[1]],[self.segments[i-1].point[2], segment.point[2]], 'b-')"""ax1.plot([self.segments[i-1].point[2], segment.point[2]],[self.segments[i-1].point[0], segment.point[0]],[self.segments[i-1].point[1], segment.point[1]], 'b-')"""# Connect the last segment to the base point"""ax1.plot([self.basePoint[2], self.segments[0].point[2]],[self.basePoint[0], self.segments[0].point[0]],[self.basePoint[1], self.segments[0].point[1]], 'b-')"""ax1.plot([self.basePoint[0], self.segments[0].point[0]],[self.basePoint[1], self.segments[0].point[1]],[self.basePoint[2], self.segments[0].point[2]], 'b-')# Start point#ax1.scatter(self.basePoint[2], self.basePoint[0], self.basePoint[1], c='g')ax1.scatter(self.basePoint[0], self.basePoint[1], self.basePoint[2], c='g')ax1.scatter(self.targetpoint[0],self.targetpoint[1],self.targetpoint[2], c='r',alpha=0.6, s=100)ax1.set_ylabel('y-axis')ax1.set_zlabel('z-axis')ax1.set_xlabel('x-axis')# Set the view angle so that the z-axis is pointing upwardsax1.view_init(elev=45., azim=45.)plt.pause(0.01)def extract_coordinates(self,s):# 使用正则表达式匹配x, y, z的值# 注意：负号前面加上了反斜杠进行转义# 使用正则表达式提取实数值，包括负号pattern = r'−?\d+\.\d+'matches = re.findall(pattern, s)values = [float(match.replace('−', '-')) for match in matches]x, y, z=values return x, y, zdef show(self):self.plot()self.fig.canvas.mpl_connect('button_press_event', self.on_click)  # 连接点击事件self.fig.canvas.mpl_connect('motion_notify_event', self.on_motion) plt.show()def on_motion(self,event):if event.inaxes is not None:x, y = event.xdata, event.ydatasting = self.ax1.format_coord(x, y)              x,y,z=self.extract_coordinates(sting)#print(x,y,z) self.mousep=(x,y,z)def on_click(self, event):# 检查点击事件是否在坐标轴内if event.inaxes is not None:print(f'Clicked on axis {event.inaxes}')# 触发你的函数print(self.mousep)if not type(self.mousep) == type(None):           x,y,z=self.mousepprint("compute")self.compute(x, y, z)self.plot()# 获取点击的坐标值#self.compute(x, y, z)# 重绘图形#

可以通过如下步骤实现逆解：

• 添加关节段：通过addSegment方法，我们可以为机械臂添加多个关节段，每个关节段都有自己的长度和初始角度。

• 检查可达性：isReachable方法检查目标位置是否在机械臂的可达范围内。

• 迭代计算：iterate方法执行一次FABRIK算法迭代，调整关节位置以接近目标。

• 绘图显示：plot方法用于在3D空间中绘制机械臂的当前状态，show方法则显示最终的图形界面，并允许用户通过点击来选择目标位置。

• 事件处理：on_click和on_motion方法用于处理用户的点击和鼠标移动事件，以便动态地调整目标位置。

        if __name__ == "__main__":        arm = FabrikSolver3D()    arm.addSegment(0, 0, 0)arm.addSegment(50, 0, 0)arm.addSegment(50, 0, 0)arm.addSegment(50, 0, 0)arm.addSegment(50, 0, 0)arm.compute(50, 50, 100)    arm.show()

结论

通过这个Python实现，我们可以看到FABRIK算法在解决3D逆运动学问题中的强大能力。它不仅能够快速找到解决方案，还能够实时响应用户的交互，这在模拟和实际应用中都是非常有价值的。接下来我们尝试丰富这个算法，在各关节添加约束，并应用到6轴机械臂的IK计算中，看看能否获得预期效果。

[------------本篇完-------------]

PS.扩展阅读

————————————————————————————————————————

对于python机器人编程感兴趣的小伙伴，可以进入如下链接阅读相关咨询

ps1.六自由度机器人相关文章资源

(1) 对六自由度机械臂的运动控制及python实现（附源码)

(2) N轴机械臂的MDH正向建模，及python算法

ps2.四轴机器相关文章资源

(1) 文章：python机器人编程——用python实现一个写字机器人

（2）python机器人实战——0到1创建一个自动是色块机器人项目-CSDN直播

(3)博文《我从0开始搭建了一个色块自动抓取机器人，并实现了大模型的接入和语音控制-(上基础篇)》的vrep基础环境
(3)博文《我从0开始搭建了一个色块自动抓取机器人，并实现了大模型的接入和语音控制-(上基础篇)》的vrep基础环境
(4)实现了语音输入+大模型指令解析+机器视觉+机械臂流程打通

ps3.移动小车相关文章资源

（1）python做了一个极简的栅格地图行走机器人，到底能干啥？[第五弹]——解锁蒙特卡洛定位功能-CSDN博客
(2) 对应python资源：源码地址

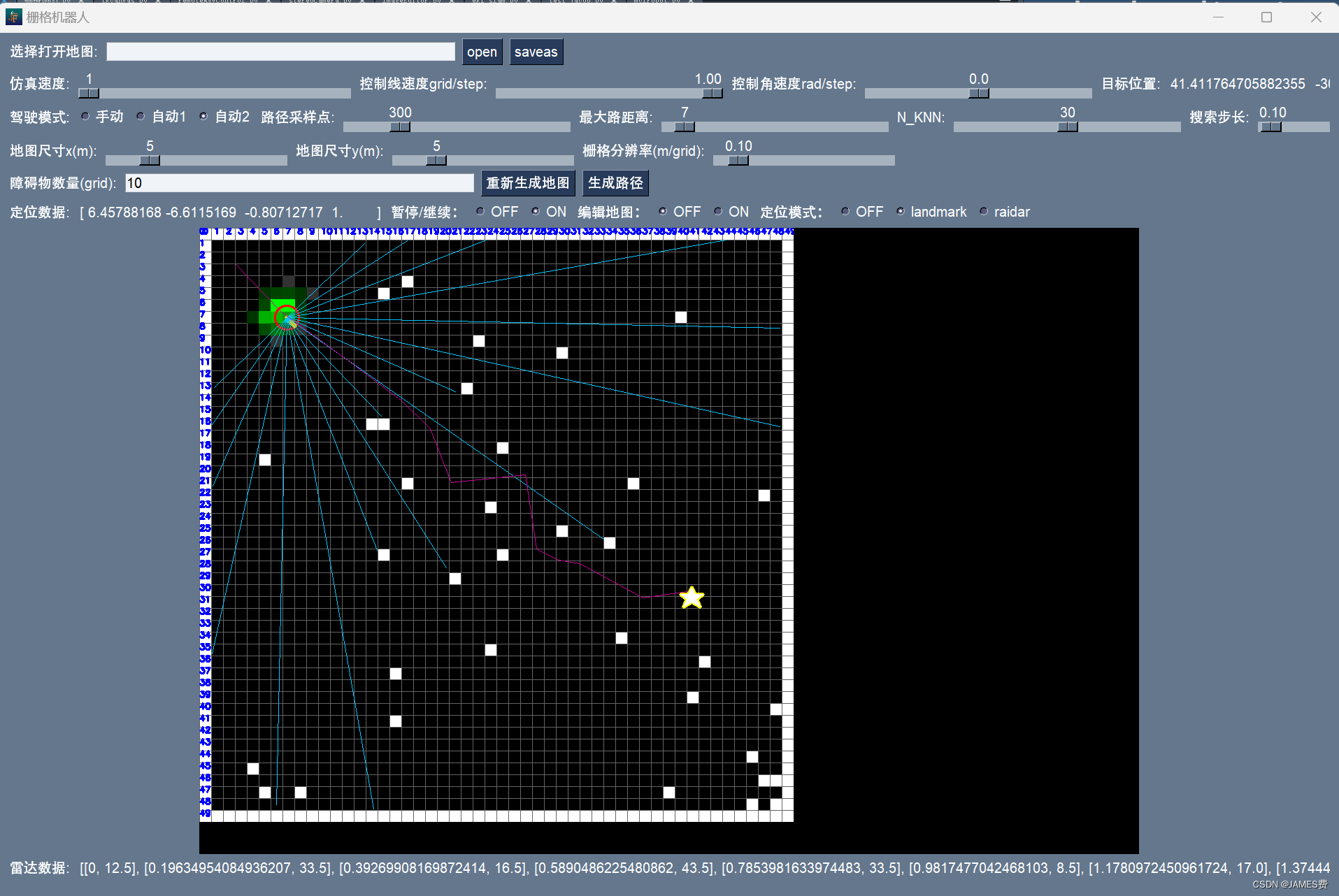
(3)python机器人编程——差速AGV机器、基于视觉和预测控制的循迹、自动行驶（上篇）_agv编程-CSDN博客
(4)python机器人编程——差速AGV机器、基于视觉和预测控制的循迹、自动行驶（下篇）_agv路线规划原则python-CSDN博客
对应python及仿真环境资源：源码链接

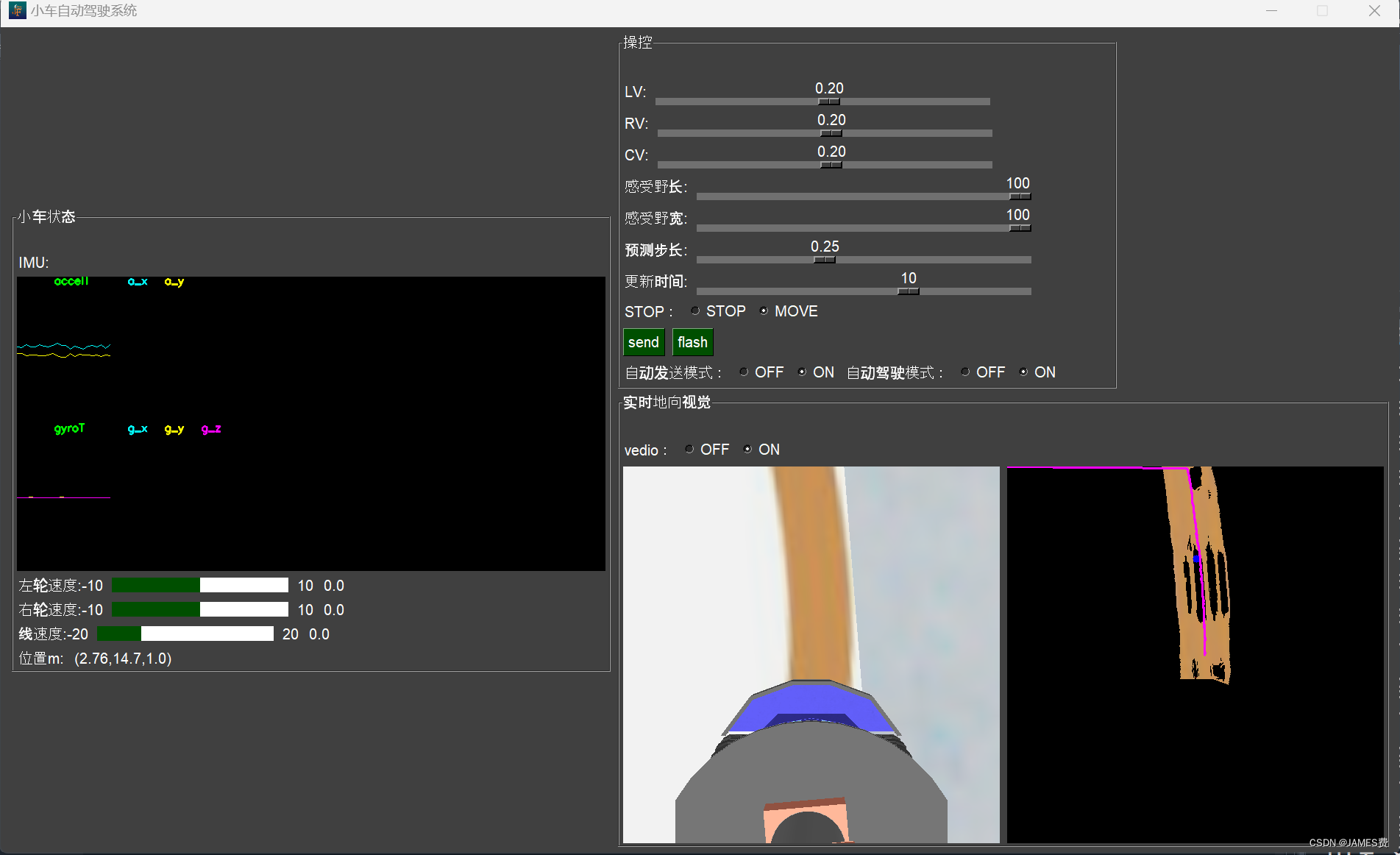
ps3.wifi小车控制相关文章资源

web端配套资源源代码已经上传(竖屏版)，下载地址
仿真配套资源已经上传：下载地址
web端配套资源源代码已经上传(横屏版)，下载地址

在这里插入代码片