Educational Codeforces Round 88 E. Modular Stability
题目链接
Educational Codeforces Round 88 E. Modular Stability
思路
对于任意的非负整数 x x x,我们要满足 x % a % b = x % b % a x \% a \% b = x \% b \% a x%a%b=x%b%a。因为 a < b a < b a<b,所以只有 b b b为 a a a的倍数时才满足条件。
因此,我们可以枚举最小的 a a a,求出值域范围内有多少个它的倍数,然后使用组合数学计算答案即可。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int N = 5e5 + 5, M = 1e6 + 5;
const int mod = 998244353;
const int inf = 0x3f3f3f3f3f3f3f3f;
int n, k;
int fac[N], infac[N];
int qmi(int a, int b, int c)
{int res = 1;while (b){if (b & 1)res = res * a % c;b >>= 1;a = a * a % c;}return res;
}
void init()
{fac[0] = infac[0] = 1;for (int i = 1; i <= n; i++){fac[i] = fac[i - 1] * i % mod;infac[i] = infac[i - 1] * qmi(i, mod - 2, mod) % mod;}
}
int C(int a, int b)
{return fac[a] * infac[b] % mod * infac[a - b] % mod;
}
int MOD(int x)
{return (x % mod + mod) % mod;
}
void solve()
{cin >> n >> k;init();if (n < k){cout << 0 << endl;}else{int ans = 0;for (int i = 1; i <= n - k + 1; i++) //假设最小的a[i]为i{int num = n / i - 1;if (num < k - 1) break;ans = (ans + C(num, k - 1)) % mod;}cout << MOD(ans) << endl;}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int test = 1;// cin >> test;for (int i = 1; i <= test; i++){solve();}return 0;
}
相关文章:

Educational Codeforces Round 88 E. Modular Stability
题目链接 Educational Codeforces Round 88 E. Modular Stability 思路 对于任意的非负整数 x x x,我们要满足 x % a % b x % b % a x \% a \% b x \% b \% a x%a%bx%b%a。因为 a < b a < b a<b,所以只有 b b b为 a a a的倍数时才满足条件…...

Android中SurfaceView与GLSurfaceView 的关系
SurfaceView 与 GLSurfaceView 的关系 在 Android 开发中,SurfaceView 和 GLSurfaceView 是实现自定义渲染效果的关键组件。它们提供了不同的渲染方式,适用于不同的应用场景。我们将通过以下几个方面详细说明 SurfaceView 和 GLSurfaceView 的特点及实现…...

numpy——数学运算
一、标量——矢量 import numpy as npa 3.14 b np.array([[9, 5], [2, 7]])print(a) print(b)# ---------- 四则运算 ---------- print(a b) # np.add print(a - b) # np.subtract print(a * b) # np.multiply print(a / b) # np.divide 二、矢量——矢量 import nump…...

【工具】Charles对360浏览器抓包抓包
Charles 和 switchy sharp 配合,可以对 Chrome 进行抓包也可以配合对360安全浏览器抓包。 本文以Windows 电脑中的配置为例,介绍如何实现抓包。(Mac中操作基本一致) 1.安装Charles 可根据自己的电脑下载对应的版本:…...

【HarmonyOS】判断应用是否已安装
【HarmonyOS】判断应用是否已安装 前言 在鸿蒙中判断应用是否已安全,只是通过包名是无法判断应用安装与否。在鸿蒙里新增了一种判断应用安装的工具方法,即:canOpenLink。 使用该工具函数的前提是,本应用配置了查询标签querySch…...

Qt Designer客户端安装和插件集(pyqt5和pyside2)
GitHub - PyQt5/QtDesignerPlugins: Qt Designer PluginsQt Designer Plugins. Contribute to PyQt5/QtDesignerPlugins development by creating an account on GitHub.https://github.com/PyQt5/QtDesignerPlugins 一、下载客户端 https://github.com/PyQt5/QtDesigner/rel…...
基于边缘计算的智能门禁系统架构设计分析
案例 阅读以下关于 Web 系统架构设计的叙述,回答问题1至问题3。 【说明】 某公司拟开发一套基于边缘计算的智能门禁系统,用于如园区、新零售、工业现场等存在来访被访业务的场景。来访者在来访前,可以通过线上提前预约的方式将自己的个人信息…...

鸿蒙实现相机拍照及相册选择照片
前言: 1.如果你的应用不是存储类型或者相机拍照类型,你就需要用 kit.CameraKit Api 实现相机拍照和相册选择照片功能,如果你不用这个的话,你使用 picker.PhotoViewPicker ,你就需要申请权限,那你提交应用审…...

「C/C++」C++17 之 std::filesystem::recursive_directory_iterator 目录及子目录迭代器
✨博客主页何曾参静谧的博客📌文章专栏「C/C」C/C程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasoli…...

智能EDA小白从0开始 —— DAY30 冉谱微RFIC-GPT
在科技日新月异的今天,电子设计自动化(EDA)行业正以前所未有的速度推动着半导体产业的革新与发展,引领着全球电子产业迈向更加智能化、高效化的未来。作为EDA领域的佼佼者,冉谱公司始终站在技术创新的前沿,…...

Android -- 调用系统相册之图片裁剪保存
前言 最近线上反馈,部分vivo手机更换头像时调用系统相册保存图片失败,经本人测试,确实有问题。 经修复后,贴出这块的代码供小伙伴们参考使用。 功能 更换头像选择图片: 调用系统相机拍照,调用系统图片…...

读《道德经》让人感到心胸气闷?董仲舒篡改
为什么读《道德经》会让人感到心胸气闷?难道是董仲舒篡改所致? 作为世界智慧源头的《老子》,享誉古今中外,是世界历史上最伟大的著作之一。 然而,很多人读《道德经》时会感到心胸气闷,这究竟是为什么呢&am…...
D52【python 接口自动化学习】- python基础之模块与标准库
day52 标准库 学习日期:20241029 学习目标:模块与标准库 -- 67 标准库:Python默认提供的便携功能有哪些? 学习笔记 标准库中的常见组件 如何通过官方文档学习标准 from urllib.request import urlopen with urlopen(http://ww…...

基于yolov8的布匹缺陷检测系统,支持图像、视频和摄像实时检测【pytorch框架、python源码】
更多目标检测和图像分类识别项目可看我主页其他文章 功能演示: 基于yolov8的布匹缺陷检测系统,支持图像、视频和摄像实时检测【pytorch框架、python源码】_哔哩哔哩_bilibili (一)简介 基于yolov8的布匹缺陷检测系统是在 PyTo…...

SQL Server 中,将单行数据转换为多行数据
在 SQL Server 中,将单行数据转换为多行数据通常涉及到将某个字段中的逗号分隔的值拆分成多行。这种操作通常称为“拆分”或“展开”(Explode)。以下是一些常用的方法来实现这一目标: 1. 使用内置函数 STRING_SPLIT 从 SQL Serv…...

解决数组两数之和问题与逻辑推理找出谋杀案凶手
给定一个整数数组nums和一个整数目标值target(2<nums.length<10^4),请你在该数组中找出和为目标值target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。 你可以按任意顺序返…...
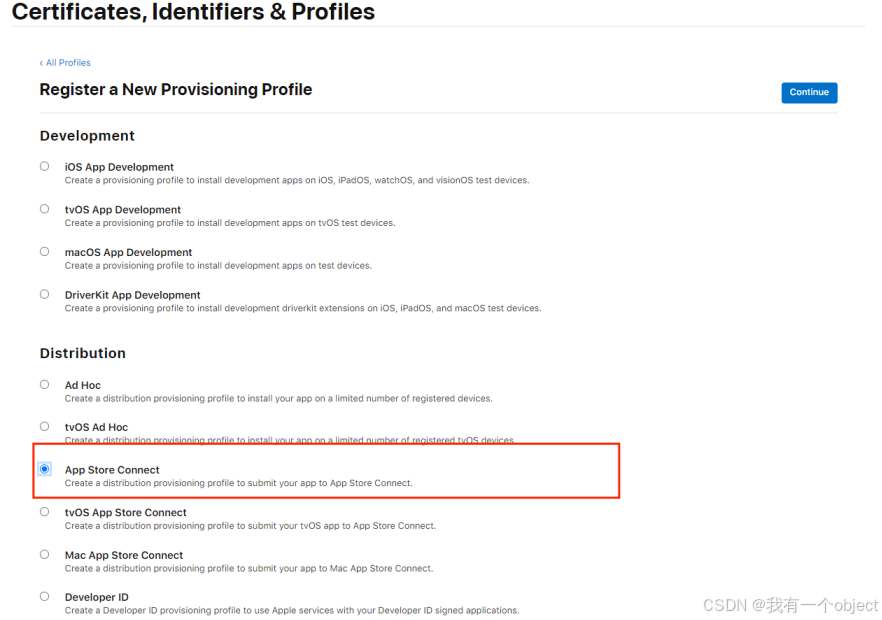
uniapp的IOS证书申请(测试和正式环境)及UDID配置流程
1.说明 本教程只提供uniapp在ios端的证书文件申请(包含正式环境和开发环境)、UDID配置说明,请勿用文档中的账号和其他隐私数据进行测试,请勿侵权! 2.申请前准备 证书生成网站:苹果应用上传、解析&#x…...

windows 安装apex_Nvidia Apex安装
参见windows 安装apex_Nvidia Apex安装 重点: 1、在安装前先检查一下,电脑的cuda版本和pytorch内的cuda版本是否一样,不一样的话就把低版本的进行升级; $ git clone https://github.com/NVIDIA/apex$ cd apex2、在保证cuda版本一…...

Laravel5 抓取第三方网站图片,存储到本地
背景 近期发现,网站上的部分图片无法显示, 分析发现,是因为引用的第三方网站图片(第三方服务器证书已过期) 想着以后显示的方便 直接抓取第三方服务器图片,转存到本地服务器 思路 1. 查询数据表࿰…...

DevOps和CI/CD以及在微服务架构中的作用
DevOps 和 CI/CD 是现代软件开发和运维中两个重要的概念,它们之间有紧密的联系,但也有不同的侧重点。以下是对这两个概念的详细介绍和比较。 1. DevOps 定义: DevOps 是一种文化、运动和实践,旨在通过促进开发(Development)和运维(Operations)团队之间的协作,提升软…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
