大语言模型的Scaling Law【Power Low】
NLP-大语言模型学习系列目录
一、注意力机制基础——RNN,Seq2Seq等基础知识
二、注意力机制【Self-Attention,自注意力模型】
三、Transformer图文详解【Attention is all you need】
四、大语言模型的Scaling Law【Power Low】
文章目录
- NLP-大语言模型学习系列目录
- 一、什么是 Scaling Law
- 二、 Scaling Law的应用
- (1)最佳模型参数,数据量求解方法
- (2)LLaMA3.1中的Scaling Law
- (3)计算实例【根据计算量和数据量,求最佳模型大小】
- 三、未来挑战
- 参考资料
一、什么是 Scaling Law
Scaling Law(缩放法则)是人工智能和机器学习中一类理论,它描述了随着模型规模(例如参数数量)、训练数据量、计算资源的增加,模型性能如何提升的规律。简单来说,Scaling Law 研究的是模型性能与模型规模之间的关系。
定义【Scaling Law】1
在生成模型中被广泛观察到的现象,对于计算量C,模型参数量N和数据大小D,当不受另外两个因素影响时,模型的性能与每个因素都呈幂律关系:
- 性能 ∝ N α \propto N^{\alpha} ∝Nα
- 性能 ∝ D β \propto D^{\beta} ∝Dβ
- 性能 ∝ C γ \propto C^{\gamma} ∝Cγ
这些公式中的 α、β、γ 是对应维度的缩放指数。通常模型性能可以用Test Loss来表示,Loss越小说明模型性能越好。
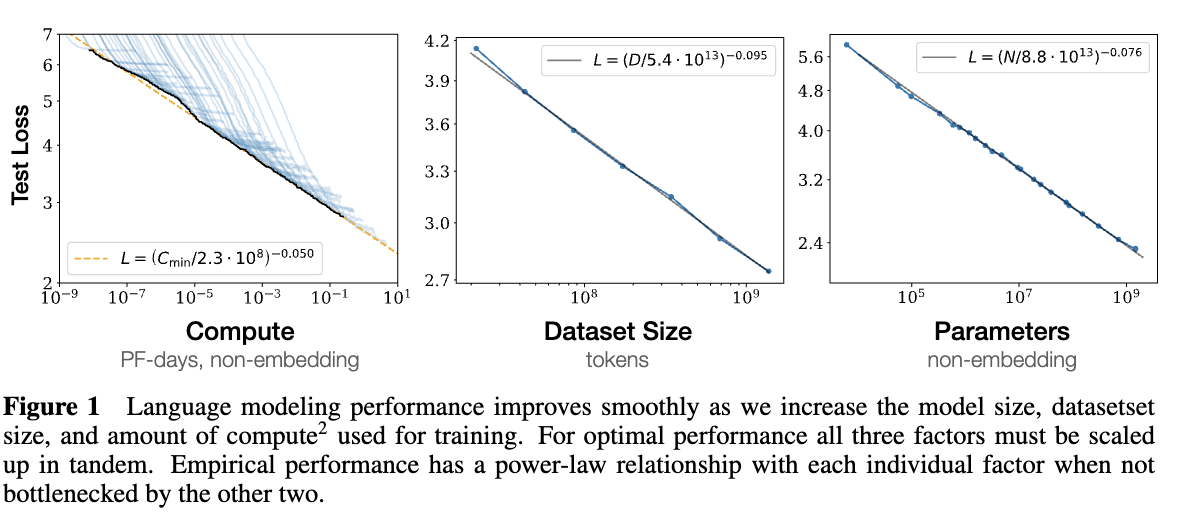
Scaling Law背后的基本思想是:模型的性能可以通过简单的扩展(例如增加模型参数、训练数据或计算资源)来不断提升,并且这种提升往往遵循一定的幂律关系。通过研究这种关系,研究者可以预测模型在不同规模下的性能表现,指导大模型的设计和训练。
二、 Scaling Law的应用
Scaling Law总结出来的一个规律是:
C ≈ 6 N D C\approx6ND C≈6ND
其中C是计算量,N是参数量,D是训练数据量。举个例子:
假设一个模型有 10亿个参数( N = 1 0 9 N=10^9 N=109 ), 并且训练数据集的规模是 D = 1 0 12 \mathrm{D}=10^{12} D=1012 (1万亿个 token).使用公式 C = 6ND, 总的计算量就是:
C = 6 × 1 0 9 × 1 0 12 = 6 × 1 0 21 F L O P s C=6 \times 10^9 \times 10^{12}=6 \times 10^{21} \mathrm{FLOPs} C=6×109×1012=6×1021FLOPs
这表明要训练这个模型, 大约需要 6 × 1 0 21 6\times 10^{21} 6×1021 次浮点运算。

这个规律有什么用呢?通过前面的Scaling Law我们知道,训练大模型时,增加模型的参数量或者训练的数据量,模型性能会得到提升。但是我们并不能无止境的增加,因为现实训练模型收到计算量的制约,训练一个语言大模型是很费钱的。所以当给定一个计算量budget,我们怎么分配N和D得到一个最好的模型呢?
(1)最佳模型参数,数据量求解方法
上面的问题可以建模为如下的优化问题:
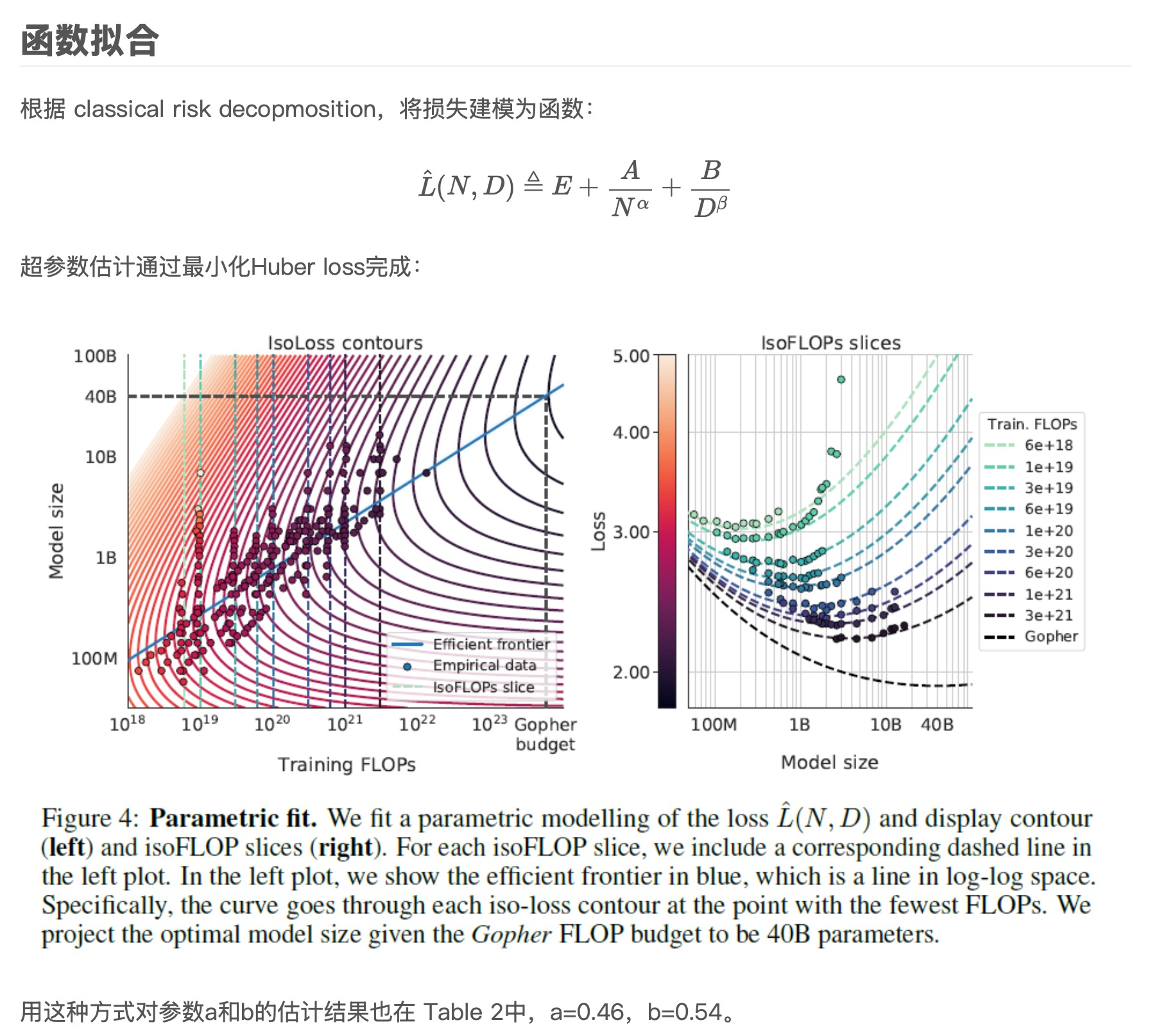
N o p t ( C ) , D o p t ( C ) = argmin N , D s.t. FLOPs ( N , D ) = C L ( N , D ) , L ^ ( N , D ) ≜ E + A N α + B D β . N_{opt}(C),D_{opt}(C)=\underset{N,D\text{ s.t. FLOPs}(N,D)=C}{\operatorname*{argmin}}L(N,D),\\ \hat{L}(N,D)\triangleq E+\frac A{N^\alpha}+\frac B{D^\beta}. Nopt(C),Dopt(C)=N,D s.t. FLOPs(N,D)=CargminL(N,D),L^(N,D)≜E+NαA+DβB.
这个多变量问题怎么解呢?主要有三种方法:
- 固定模型大小,改变训练数据
- 固定计算量,改变模型大小
- 拟合幂律曲线
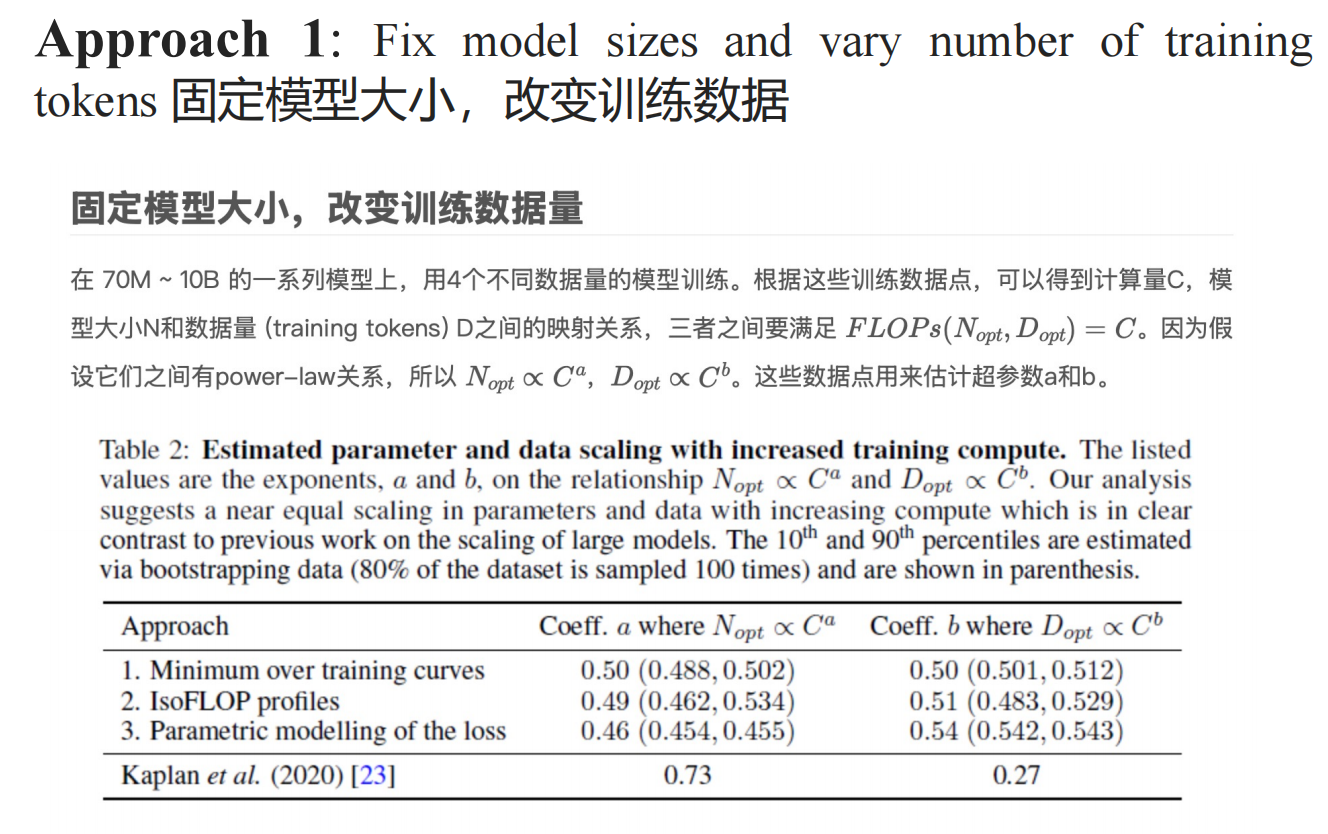
根据上表的结果,得出a=0.5,b=0.5

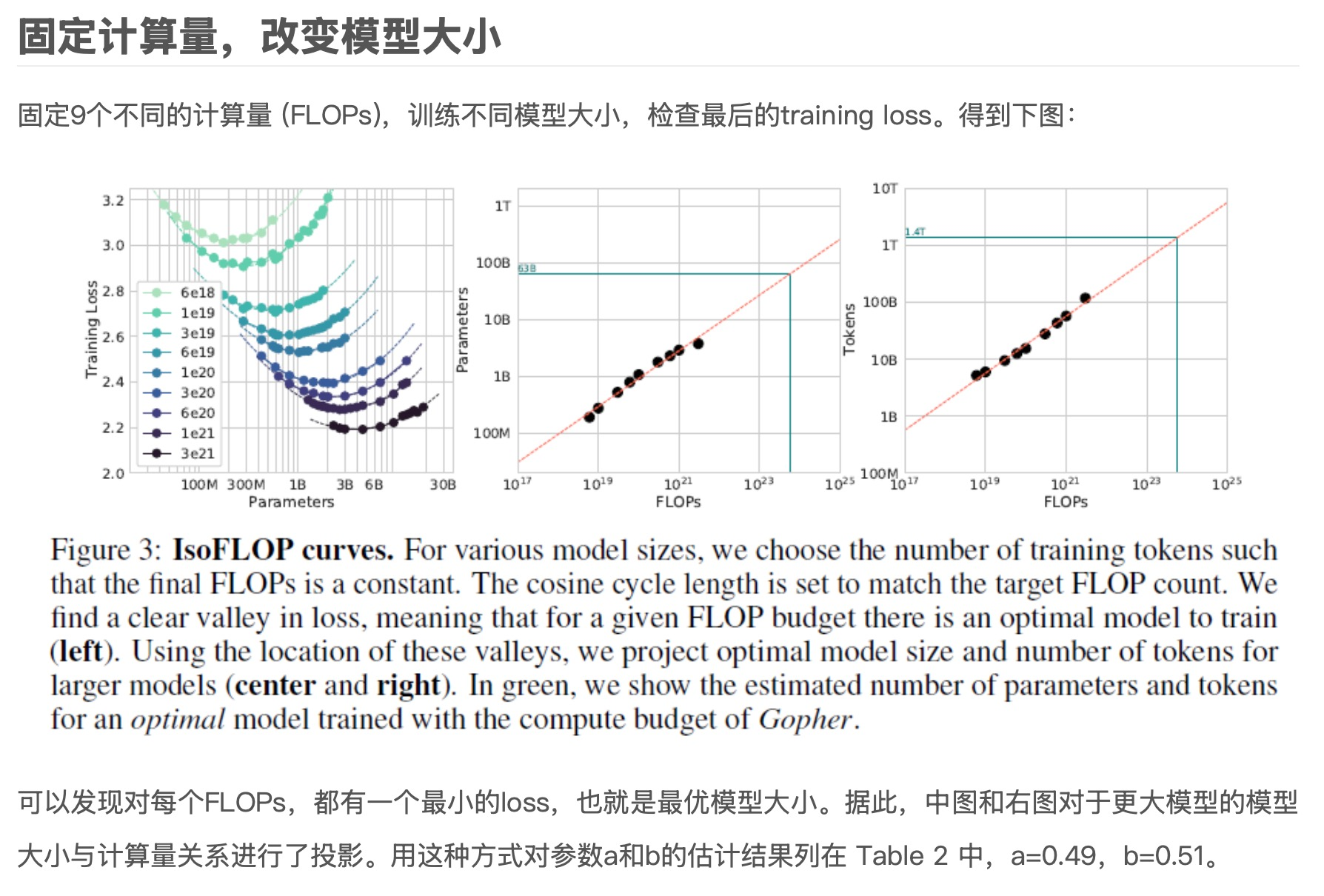 根据图3右边两图所得到的点,向外延伸,可以得到给定计算量C最佳的N、D.
根据图3右边两图所得到的点,向外延伸,可以得到给定计算量C最佳的N、D.
(2)LLaMA3.1中的Scaling Law
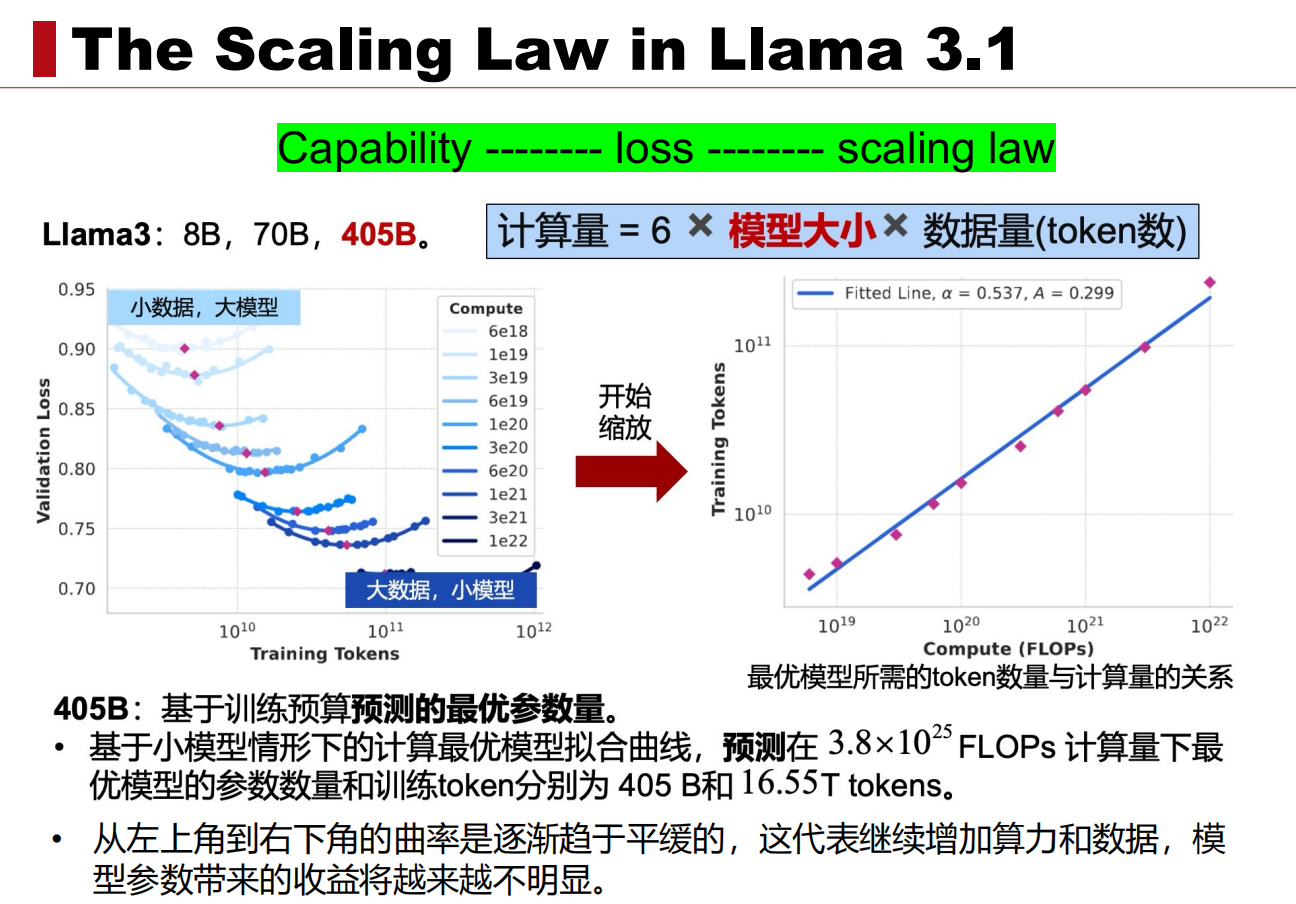
如下图所示,是LLaMA3.1中的Scaling Law,LLaMA3.1发布了3个模型,分别是8B,70B,405B.这个405B是怎么定下来的呢,难道是领导拍脑袋想出来的吗(国内可能是hh).显然他们做了实验,先在小数据和小模型上进行实验(左图),然后根据实验结果画出Scaling Law曲线,找到对应计算量的最优模型大小和最优训练数据量。
(3)计算实例【根据计算量和数据量,求最佳模型大小】
例:
- 假设你有1000张H100显卡,并且可以用6个月。
- 假设你有10T的数据。
- 那么你应该训练多大的模型?

另一种更快的估计方法:

三、未来挑战
尽管 Scaling Law 提供了重要的理论指导,仍然存在一些挑战:
- 计算成本问题:大规模扩展模型的参数和训练数据通常需要极高的计算成本。虽然 Scaling Law 提供了理论依据,但大规模训练的实际成本可能难以承受。
- 数据质量:Scaling Law 假设数据量的增加会提升模型性能,但在实际应用中,数据的质量同样至关重要,低质量数据可能会导致性能下降甚至模型偏差。
- 性能饱和:Scaling Law 研究表明,性能提升并不是无限的,通常会在某个点达到瓶颈。因此,研究者需要找到其他方法(如新架构、知识蒸馏)来进一步提高性能。
参考资料
Scaling Laws for Neural Language Models【paper】 ↩︎
相关文章:

大语言模型的Scaling Law【Power Low】
NLP-大语言模型学习系列目录 一、注意力机制基础——RNN,Seq2Seq等基础知识 二、注意力机制【Self-Attention,自注意力模型】 三、Transformer图文详解【Attention is all you need】 四、大语言模型的Scaling Law【Power Low】 文章目录 NLP-大语言模型学习系列目录一、什么是…...

windows环境下,使用docker搭建redis集群
参考: https://blog.csdn.net/weixin_46594796/article/details/137864842 https://www.cnblogs.com/niceyoo/p/14118146.html 史上最详细Docker搭建Redis Cluster集群环境 值得收藏 每步都有图,不用担心学不会-腾讯云开发者社区-腾讯云 一、基础环境描述 宿主机:192.168…...

Python(pandas库3)
函数 随机抽样 语法: n:要抽取的行数 frac:抽取的比例,比如 frac0.5,代表抽取总体数据的50% axis:示在哪个方向上抽取数据(axis1 表示列/axis0 表示行) 案例: 输出结果都为随机抽取。 空…...

WPF+MVVM案例实战(十)- 水波纹按钮实现与控件封装
文章目录 1、运行效果1、封装用户控件1、创建文件2、依赖属性实现2、使用封装的按钮控件1.主界面引用2.按钮属性设置3 总结1、运行效果 1、封装用户控件 1、创建文件 打开 Wpf_Examples 项目,在 UserControlLib 用户控件库中创建按钮文件 WaterRipplesButton.xaml ,修改 Us…...

数据结构————map,set详解
今天带来map和set的详解,保证大家分清楚 一,概念 map和set是一种专门用来搜索的容器或数据结构 map能存储两个数据类型,我们称之为<key-value>模型 set只能存储一个数据类型,我们称之为纯<key>模型 它们的效率都非…...

fdisk - Linux下的磁盘分区利器
文章目录 前言一、安装和启动二、基本命令2.1 查看分区表2.2 删除分区2.3 创建新分区2.4 更改分区类型2.5 其他指令 三、注意事项四、其他相关工具 前言 在Linux系统中,磁盘管理是维护系统性能和数据安全的重要环节。fdisk 是一个强大的命令行工具,专门…...

or-tools优化库记录
介绍 Or-tools是谷歌人工智能系列的运筹优化包,是一个用于优化的开源软件套件,针对性地解决车辆路线问题、流程优化、整数和线性规划以及约束规划等问题。 官网地使用说明比我详细,我就不多逼逼了 使用说明网址: https://develo…...

M1 Pro MacBook Pro 上的奇遇:Rust 构建失败,SIGKILL 惊魂记
你是否也曾在 M1 Pro MacBook Pro 上遇到过离奇的编译问题?这次我遇到的奇葩问题绝对值得一聊——一个仅在苹果M1 Pro上的神秘构建失败。其他设备都安然无恙,唯独它!折腾了一番,终于让我揭开了这“阴谋”的真相。 问题描述 在运…...

重构商业生态:DApp创新玩法与盈利模式的深度剖析
随着区块链技术的发展,DApp(去中心化应用)正在从实验走向成熟。DApp以去中心化、透明性和不可篡改性为基础,结合智能合约,逐步改变传统商业运作模式,创造新的市场生态。本文将从DApp的独特优势、创新玩法和…...

2024首届亚洲国际电影节圆满落下帷幕
10月26日下午,2024首届亚洲国际电影节颁奖典礼在中国•澳门隆重举行。在这座充满时尚感的“东亚文化之都”,一座座金鹮奖杯,汇聚起全球电影艺术的荣耀之光,见证着无数电影梦想的傲然绽放。明星云集欢聚一堂,同庆澳门回…...

【Mybatis】动态SQL+配置文件+数据库连接池+企业规范(10)
本系列共涉及4个框架:Sping,SpringBoot,Spring MVC,Mybatis。 博客涉及框架的重要知识点,根据序号学习即可。 目录 本系列共涉及4个框架:Sping,SpringBoot,Spring MVC,Mybatis。 博客涉及框架的重要知识点,根据序号学习即可。 …...

layui扩展组件之----右键菜单
源码:rightmenu.js layui.define([element], function (exports) {let element layui.element;const $ layui.jquery;let MOD_NAME rightmenu;let RIGHTMENUMOD function () {this.v 1.0.0;this.author raowenjing;};String.prototype.format function () {…...

ue5实现数字滚动增长
方法1 https://www.bilibili.com/video/BV1h14y197D1/?spm_id_from333.999.0.0 b站教程 重写loop节点 方法二 写在eventtick里...

Flink(一)
目录 架构处理有界与无界数据部署应用到任意地方运行任意规模应用利用内存性能 流应用流处理应用的基本组件流状态时间 应用场景事件驱动应用事件驱动应用的优势Flink如何支持事件驱动应用? 典型的事件驱动示例 数据分析应用流式分析应用的优势?Flink 如…...

kaggle 数据集下载
文章目录 kaggle 数据集下载(1) 数据集下载(2) 手机号验证 kaggle 数据集下载 这两天想学习 kaggle 赛事 把深度学习相关的内容自己给过一遍,快忘得差不多了,惭愧。 参考了好多帖子,使用命令行…...

Linux shell编程学习笔记87:blkid命令——获取块设备信息
0 引言 在进行系统安全检测时,我们需要收集块设备的信息,这些可以通过blkid命令来获取。 1 blkid命令的安装 blkid命令是基于libblkid库的命令行工具,可以在大多数Linux发行版中使用。 如果你的Linux系统中没有安装blkid命令,…...

wireshark筛选条件整理
Wireshark筛选条件整理 一、MAC地址过滤二、IP地址过滤三、端口过滤四、协议筛选五、数据分析1、整体2、frame数据帧分析3、 Ethernet II 以太网4、IP协议5、TCP6、HTTP7、ARP8、DLEP动态链接交换协议 六、统计-协议分级(统计包占比) and && 、 …...

基于现代 C++17 的模块化视频质量诊断处理流程设计
文章目录 0. 引言1. 原始设计分析2. 新的设计思路2.1 定义通用的检测接口2.2 使用 std::function 和 std::any 管理检测模块2.3 构建可动态配置的检测管道 3. 示例实现3.1 定义检测接口和模块3.1.1 检测接口3.1.2 信号检测模块3.1.3 冻结检测模块3.1.4 其他检测模块 3.2 构建检…...

高级java每日一道面试题-2024年10月23日-JVM篇-说一下JVM有哪些垃圾回收算法?
如果有遗漏,评论区告诉我进行补充 面试官: 说一下JVM有哪些垃圾回收算法? 我回答: 在 Java 虚拟机 (JVM) 中,垃圾回收 (Garbage Collection, GC) 是一项非常重要的功能,用于自动管理应用程序的内存。JVM 采用多种垃圾回收算法来决定何时以及如何回收…...

高效文本编辑与导航:Vim中的三种基本模式及粘滞位的深度解析
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
