当前位置： 首页 > news >正文

开源一个开发的聊天应用与AI开发框架，集成 ChatGPT，支持私有部署的源码

news 2026/2/8 18:07:05

大家好，我是一颗甜苞谷，今天分享一个开发的聊天应用与AI开发框架，集成 ChatGPT，支持私有部署的源码。

介绍

当前系统集成了ChatGPT的聊天应用，不仅提供了基本的即时通讯功能，还引入了先进的AI技术，使得交流更加智-能化。

一句话囊括：

 智-能化的聊天体验，由内而外的技术创新。

特点

  • 高-效的应用构建：基于Vite5，快速构建应用，提升开发效率。
  • 安-全的身份验证：通过JWT权限控制，确保用户安-全。
  • AI语言模型：接入OpenAI，提供智-能化的对话体验。
  • 便捷的聊天记录：支持聊天记录截图分享，沟通更灵活。
  • 强大的通讯能力：基于IM即时通讯SDK，稳定可靠。
  • 智-能模式切换：自动适应光明与黑暗模式，保护用户视力。
  • 丰富的文本支持：支持Markdown渲染和代码高亮，适合技术用户。
  • 多语言支持：提供英语与简体中文，满足不同用户需求。
  • 代码规范：采用Prettier与ESLint，代码质量高。
  • 无缝社交体验：通过GitHub快速登录，简化用户操作。
  • 桌面应用支持：提供Electron版本，支持macOS与Windows。

技术架构

采用了当前流行的技术栈，包括Vue3、Vite5和Electron，确保了应用的高性能和良好的用户体验。

部署方式

部署非常简单，只需在本地环境中安装Node.js 18.20+，然后通过以下命令即可完成安装和启动：

pnpm install
pnpm dev

开源协议

遵循MIT协议，可以自由地用于商业和非商业项目。

即刻体验一波

许多功能都可以通过在线预览体验，包括但不限于：

  • 智-能的ChatGPT机器人对话体验。
  • 便捷的聊天记录截图和分享。
  • 多语言界面的切换。
  • 基于GitHub的快速登录流程。
  • 桌面应用的下-载和体-验。

结语

作为一个集成了ChatGPT的聊天应用，不仅提供了丰富的功能，还通过AI技术提升了用户的沟通体验。

需要的小伙伴直接点击如下链接免费获取
链接：https://pan.quark.cn/s/bd19027e2d38

相关文章：

开源一个开发的聊天应用与AI开发框架，集成 ChatGPT，支持私有部署的源码

大家好，我是一颗甜苞谷，今天分享一个开发的聊天应用与AI开发框架，集成 ChatGPT，支持私有部署的源码。 介绍 当前系统集成了ChatGPT的聊天应用，不仅提供了基本的即时通讯功能，还引入了先进的AI技术&#x…...

编程日记 2024/10/30 8:06:10

开发了一个成人学位英语助考微信小程序

微信小程序名称：石榴英语 全称：石榴英语真题助手 功能定位 北京成人学士学位英语辅助学习工具，包含记高频单词，高频词组，专项练习，模拟考试等功能。 开发背景 个人工作需要提高学习英文水平&#xff…...

编程日记 2024/10/30 8:05:09

LeetCode16:最接近的三数之和

原题地址：. - 力扣（LeetCode） 题目描述 给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例 1&#xf…...

编程日记 2024/10/30 8:02:06

VisualStudio2022配置2D图形库SFML

文章目录 1. 下载安装SFML库2. 创建C项目并配置SFML配置include目录和库目录链接SFML库配置动态链接库 3. 测试 1. 下载安装SFML库 SFML（Simple and Fast Multimedia Library）C库，适合2D游戏和图形界面，提供了以下模块&#xff1…...

编程日记 2024/10/30 8:00:05

「Mac畅玩鸿蒙与硬件4」鸿蒙开发环境配置篇4 - DevEco Studio 高效使用技巧

本篇将进一步介绍如何在 DevEco Studio 中高效使用各种功能，通过掌握快捷键、代码补全、调试工具等，帮助开发者在鸿蒙应用开发中大幅提升工作效率。 关键词 DevEco Studio快捷键代码补全调试工具项目导航 一、快捷键与高效操作 快捷键是提升开发效率的…...

编程日记 2024/10/30 7:59:03

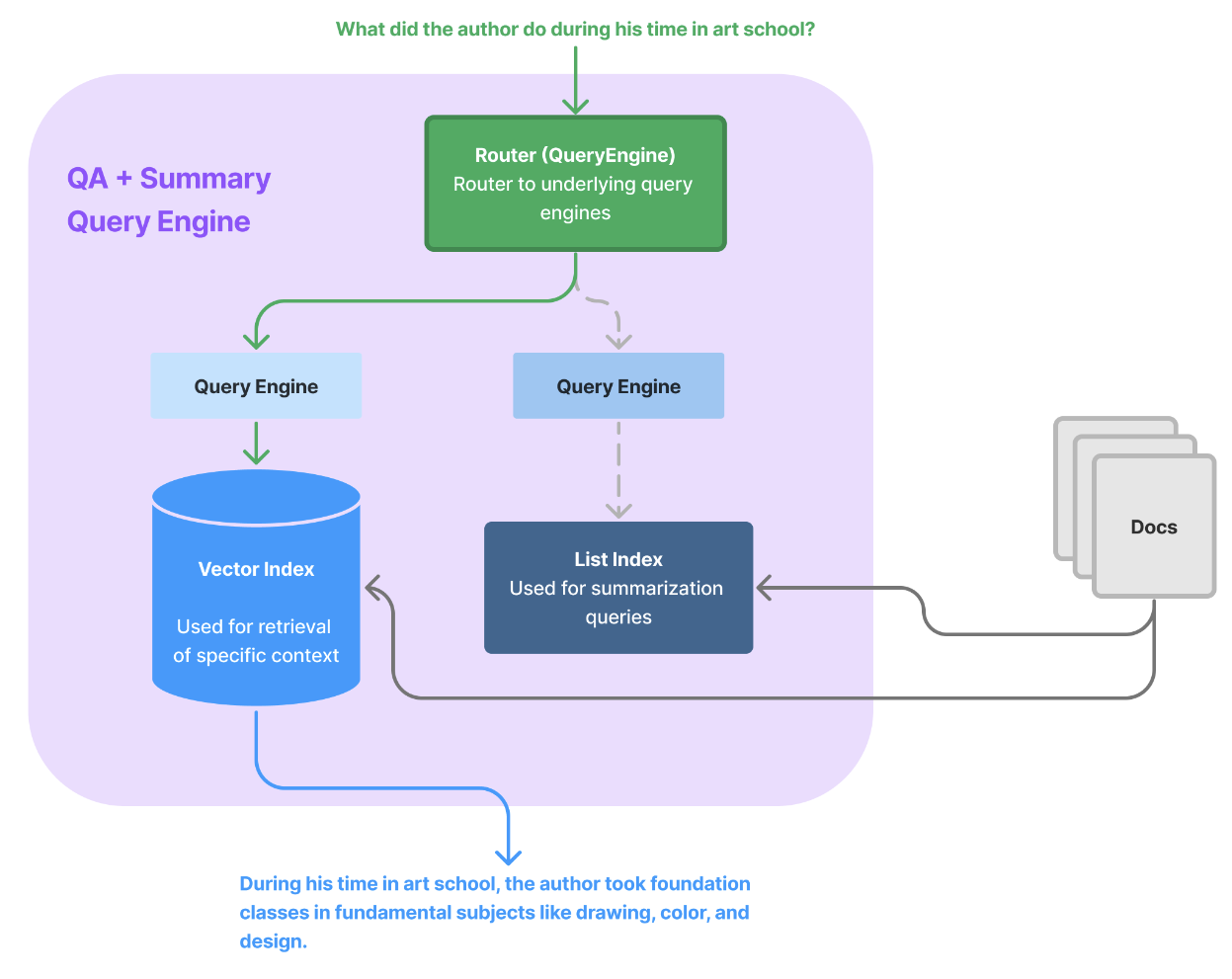
构建生产级的 RAG 系统

对 RAG 应用程序进行原型设计很容易，但要使其高性能、健壮且可扩展到大型知识语料库却很困难。 本指南包含各种提示和技巧，以提高 RAG 工作流程的性能。我们首先概述一些通用技术 - 它们按照简单到复杂的顺序进行排列。然后，我们将更深入地研…...

编程日记 2024/10/30 7:52:57

完全透彻了解一个asp.net core MVC项目模板2

这是《完全透彻了解一个asp.net core MVC项目模板》的第二篇，如果你直接进入了本篇博文而不知道上下文，请先阅读《完全透彻了解一个asp.net core MVC项目模板》的第一篇。 文章目录 一、补充几个问题1、有关导航链接和Tag Helper2、_ViewStart.cshtml与…...

编程日记 2024/10/30 7:45:50

uniapp 如何调用音频

uniapp调用音频 button点击 <view><button click"startPlay">开始播放</button></view>方法实现 startPlay() { const innerAudioContext uni.createInnerAudioContext();innerAudioContext.src /static/sounds/oqc.mp3;innerAudioContex…...

编程日记 2024/10/30 7:44:49

在Facebook运营中使用住宅IP的重要性

在当前社交媒体的浪潮中&#xff0c;Facebook作为全球最大的社交网络之一&#xff0c;吸引了数以亿计的用户。为了在这一平台上实现有效的运营和推广&#xff0c;越来越多的博主和营销人员正在寻求最佳的养号策略。其中&#xff0c;IP地址的选择显得尤为重要&#xff0c;尤其是…...

编程日记 2024/10/30 7:40:46

EJB项目如何升级SpringCloud

记录某金融机构老项目重构升级为微服务过程1 如何从EJB架构拆分微服务 这个非常有趣的过程&#xff0c;整个过程耗时大致接近半年时光&#xff0c;需要考虑到重构升级保留原来的业务线&#xff0c;而且还要考虑后续的维护成本&#xff0c;保留现有的数据库表结构&#xff0c;…...

编程日记 2024/10/30 7:39:45

HTTPS 协议原理

一.HTTPS的定义 大家在刚开始学习的时候是不是也是非常好奇HTTP与HTTPS之间有什么区别和联系&#xff0c;两者都是应用层协议&#xff0c;而HTTPS是在HTTP的基础上引入了加密层&#xff0c;从而将HTTP的明文传输进行加密&#xff0c;保障数据的安全性 二.加密与解密 定义&#…...

编程日记 2024/10/30 7:29:32

Vxe UI 表格行编辑(默认不显示编辑框,点击后可编辑)

效果: HTML代码:(type"integer"为这个,是限制只能输入正整数或负整数,英文和汉字自动转成0) <vxe-tableshow-overflowkeep-sourcev-loading"loading":data"ruleList"ref"Table":row-config"{isHover: true}"height"…...

编程日记 2024/10/30 7:28:31

移远通信闪耀2024香港秋灯展，以丰富的Matter产品及方案推动智能家居产业发展

10月27-30日&#xff0c;2024香港国际秋季灯饰展在香港会议展览中心盛大开展。 作为全球领先的物联网整体解决方案供应商&#xff0c;移远通信再次亮相&#xff0c;并重点展示了旗下支持Matter协议以及亚马逊ACK ( Alexa Connect Kit ) SDK for Matter方案的Wi-Fi模组、低功耗蓝…...

编程日记 2024/10/30 7:27:30

爬虫利器playwright

是什么 它是微软在 2020 年初开源的新一代自动化测试工具&#xff0c;其功能和 selenium 类似&#xff0c;都可以驱动浏览器进行各种自动化操作。还可以录制脚本 案列-01 运行之后我们用它自动打开的谷歌浏览器&#xff0c;打开百度&#xff0c;输入漂亮小姐姐并查找&#x…...

编程日记 2024/10/30 7:26:30

着色器的认识

知识了解&#xff1a; 着色器&#xff1a; 顶点着色器: 用来描述顶点的特性,如位置、颜色等&#xff0c;其中&#xff0c;顶点&#xff1a;是指二维或三维空间中的一个点比如交点或者端点。 片元着色器&#xff1a;用来进行逐片元处理操作&#xff0c;比如光照、颜色叠加等&…...

编程日记 2024/10/30 7:24:28

科技的成就（六十四）

591、《传奇》开始公开测试 "2001 年 9 月&#xff0c;《传奇》开始公开测试。《传奇》&#xff08;全称《热血传奇》&#xff09;是由韩国 WeMade 娱乐开发制作的大型多人在线角色扮演游戏&#xff0c;由 Delphi 编写。盛大网络于2001 年获得该游戏在中国的代理权。《传奇…...

编程日记 2024/10/30 7:23:27

银行信贷风控专题：Python、R 语言机器学习数据挖掘应用实例合集：xgboost、决策树、随机森林、贝叶斯等...

全文链接&#xff1a;https://tecdat.cn/?p38026 分析师&#xff1a;Fanghui Shao 在当今金融领域&#xff0c;风险管控至关重要。无论是汽车贷款违约预测、银行挖掘潜在贷款客户&#xff0c;还是信贷风控模型的构建&#xff0c;以及基于决策树的银行信贷风险预警&#xff0c;…...

编程日记 2024/10/30 7:22:25

〈壮志凌云：独行侠〉中的超高音速战机

电影《壮志凌云&#xff1a;独行侠》中使用的黑星&#xff08;Darkstar&#xff09;高超音速概念战机模型&#xff0c;虽然看起来像是科幻电影里的产物&#xff0c;但这架飞机实际上是由洛克希德马丁公司的臭鼬工厂&#xff08;Skunk Works&#xff09;设计&#xff0c;这是一家…...

编程日记 2024/10/30 7:21:23

k8s集群 ceph rbd 存储动态扩容

k8s 集群 rbd 扩容有两种方法&#xff0c;如下所示 通过StorageClass自动扩容 # kubectl get sc csi-rbd-sc -oyaml|grep allowVolumeExpansion allowVolumeExpansion: true如果搜索有如上字段&#xff0c;说明是可以自动扩容的&#xff0c;修改对应要扩容的 PVC容量&#xf…...

编程日记 2024/10/30 7:20:21

C语言笔记（指针题目）例题+图解

本文分为两部分 &#xff0c;第一部分为数组、字符串、字符指针在sizeof和strlen中的辨析&#xff0c;第二部分是一些笔试题目。若有错误&#xff0c;请批评指正。 目录 1.第一部分 1.1.数组名的使用 1.1.1一维整型数组在sizeof中的使用 1.1.2一维字符数组在sizeof中的使用…...

编程日记 2024/10/30 7:19:20

【机器视觉】单目测距——运动结构恢复

ps&#xff1a;图是随便找的&#xff0c;为了凑个封面 前言 在前面对光流法进行进一步改进&#xff0c;希望将2D光流推广至3D场景流时&#xff0c;发现2D转3D过程中存在尺度歧义问题&#xff0c;需要补全摄像头拍摄图像中缺失的深度信息&#xff0c;否则解空间不收敛&#xf…...

编程新知 2026/2/8 3:03:01

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2026/2/4 23:47:47

DIY｜Mac 搭建 ESP-IDF 开发环境及编译小智 AI

前一阵子在百度 AI 开发者大会上&#xff0c;看到基于小智 AI DIY 玩具的演示&#xff0c;感觉有点意思&#xff0c;想着自己也来试试。 如果只是想烧录现成的固件&#xff0c;乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外&#xff0c;还提供了基于网页版的 ESP LA…...

编程新知 2026/2/3 8:13:35

Neo4j 集群管理：原理、技术与最佳实践深度解析

Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...

编程新知 2025/12/27 16:43:24

ElasticSearch搜索引擎之倒排索引及其底层算法

文章目录 一、搜索引擎1、什么是搜索引擎？2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长，文件大。2.其次，树深，IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

编程新知 2026/1/30 17:10:19

Android Bitmap治理全解析：从加载优化到泄漏防控的全生命周期管理

引言 Bitmap&#xff08;位图&#xff09;是Android应用内存占用的“头号杀手”。一张1080P&#xff08;1920x1080&#xff09;的图片以ARGB_8888格式加载时&#xff0c;内存占用高达8MB&#xff08;192010804字节&#xff09;。据统计&#xff0c;超过60%的应用OOM崩溃与Bitm…...

编程新知 2026/1/8 22:17:14

Swagger和OpenApi的前世今生

Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章&#xff0c;二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑&#xff1a; &#x1f504; 一、起源与初创期&#xff1a;Swagger的诞生&#xff08;2010-2014&#xff09; 核心…...

编程新知 2026/1/25 9:08:41

HarmonyOS运动开发：如何用mpchart绘制运动配速图表

##鸿蒙核心技术##运动开发##Sensor Service Kit&#xff08;传感器服务&#xff09;# 前言 在运动类应用中&#xff0c;运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据&#xff0c;如配速、距离、卡路里消耗等&#xff0c;用户可以更清晰…...

编程新知 2026/2/2 7:49:59

回溯算法学习

一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

编程新知 2026/1/24 12:01:38

抽象类和接口（全）

一、抽象类 1.概念&#xff1a;如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象&#xff0c;这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法&#xff0c;包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中&#xff0c;⼀个类如果被 abs…...

编程新知 2026/2/5 4:38:22