““ 引用类型应用举例
| #include <iostream> //使能cin(),cout(); #include <stdlib.h> //使能exit(); #include <iomanip> //使能setbase(),setfill(),setw(),setprecision(),setiosflags()和resetiosflags(); //setbase( char x )是设置输出数字的基数,如输出进制数则用setbase(8);如输出进制数则用setbase(10);如输出进制数则用setbase(16); //setbase( char x )的参数x只能是,10和,其它参数无效,setbase对其后的cout都有影响; //当程序需要在屏幕上显示输出时,可以使用插入操作符“<<”向cout输出流中插入字符; //例如: cout<<"I love C++\n"; //当程序需要执行键盘输入时,可以使用抽取操作符“>>”从cin输人流中抽取字符; //例如: int myAge; cin>>myAge; //I/O流的常用控制符如下: //dec 置基数为; //hex 置基数为; //oct 置基数为; //left 左对齐 //right 右对齐 //setiosflags(ios::left) 左对齐,left位于ios文件中 //setiosflags(ios::right) 右对齐,right位于ios文件中 //setiosflags(ios::uppercase) 控制进制数大写输出 //resetiosflags(ios::uppercase) 控制进制数小写输出 //setfill(c) 没填充字符为c,对其后的cout都有影响; //setw(n) 设置值的输出宽度为n个字符,仅仅影响下一个数值输出; //setiosflags(ios::showpos) 强制显示正负号,对于浮点数和十进制数,正数将显示+; //setiosflags(ios::fixed) 固定以小数方式显示 //setiosflags(ios::showpoint) 若只有整数部分,则强制显示小数点; //setprecision(n) 设置浮点数小数点后有n位小数; //setiosflags(ios::scientific) 指数表示; //注意:在使用setiosflags()之后,一定要使用resetiosflags(()恢复到默认设置;否则,会出现意想不到的错误; //例如:在cout<<setiosflags(ios::fixed)被使用完后,要调用cout<<resetiosflags(ios::fixed)恢复到默认设置; //注意:cout<<setiosflags(ios::lowercase); //控制进制数小写输出,在Visual studio C++2005中,不支持该语句; //在不使用#include<iomanip>时,cout.setf(ios::right); //设置为右对齐输出; //浮点数默认显示位有效位; using namespace std; //告诉编译器使用std标准程序库; int main() { unsigned int i; //声明五符号字节型变量i; unsigned char x=1; //声明无符号字节型变量x,并初始化为; unsigned char &y=x; //声明引用y为x的别名; for(i=0;i<15;i++) { cout<<setbase(10); //采用10进制方式输出; cout<<"i="<<i<<" "; //将i的值输出到屏幕上; cout<<setbase(10); //采用10进制方式输出; cout<<"x="<<(int)x<<" "; //将x的值输出到屏幕上; cout<<setbase(16); //采用16进制方式输出; cout<<"y="<<(int)y<<endl; //将y的值输出到屏幕上; x++; } cout<<setbase(10); //重新设置为默认,采用10进制方式输出; return(0); //退出函数; }
|
相关文章:

““ 引用类型应用举例
#include <iostream> //使能cin(),cout(); #include <stdlib.h> //使能exit(); #include <iomanip> //使能setbase(),setfill(),setw(),setprecision(),setiosflags()和resetiosflags(); //setbase( char x )是设置输出数字的基数,如输出进制数则用se…...

数字图像处理 - 基于ubuntu20.04运行.NET6+OpenCVSharp项目
一、简述 上一篇Ubuntu20.04 更新Nvidia驱动 + 安装CUDA12.1 + cudnn8.9.7-CSDN博客,记录了Ubuntu20.04 更新Nvidia驱动 + 安装CUDA12.1 + cudnn8.9.7的过程,最终的目的是要这些服务器上运行.net6的程序,进行图像处理、onnxruntime推理等。 这里记录进行OpenCVSharp的安装和…...

git cherry-pick用法详解
git cherry-pick 是 Git 中一个非常有用的命令,它允许你选择一个特定的提交(commit)并将其变更应用到当前分支上。这个功能在你需要将某个分支上的某个或某些特定提交合并到另一个分支时特别有用,而不需要将整个分支合并过去。 基…...

HCIP-HarmonyOS Application Developer V1.0 笔记(一)
HarmonyOS的系统特性 硬件互助,资源共享;一次开发,多端部署;统一OS,弹性部署。 分布式软总线:分布式任务调度、分布式数据管理、分布式硬件虚拟化的基座 18N的独立设备 1个手机,8种设备(车机,…...

开发流程初学者指南——需求分析
目录 从零开始理解需求分析什么是需求分析?需求分析的目标需求分析的基本原则需求分析的各个阶段需求分析的常用方法和工具编写需求文档总结 从零开始理解需求分析 需求分析是软件开发过程中不可或缺的一环,它帮助我们明确用户的需求,确保最…...

CRM平台排名:用户体验与客户满意度的深度解析
在数字化时代,客户关系管理(CRM)系统已成为企业不可或缺的工具,它帮助企业优化客户互动,提升销售效率,并增强客户满意度。本文将深度解析各大CRM平台的用户体验和客户满意度,盘点它们的品牌介绍…...

WIFI、NBIOT、4G模块调试AT指令连接华为云物联网服务器(MQTT协议)
一、前言 随着物联网(IoT)技术的飞速发展,越来越多的设备开始连接到互联网,形成了一个万物互联的世界。在这个背景下,设备与云端之间的通讯变得尤为重要。 本文将探讨几种常见的无线通信模块——EC20-4G、Air724ug-4…...

打造自己的RAG解析大模型:(新技能)企业垂类数据标注(一)
在上一篇文章中,我们以通用版面分析服务为例,展示了从模型发布到API集成的完整流程。如果你成功完成了这些步骤,值得庆祝!这不仅意味着你已成功安装PaddleX,还掌握了利用它发布OCR和目标检测等大模型服务的能力&#x…...

怎么理解ES6 Proxy
Proxy 可以理解成,在目标对象之前架设一层 “拦截”,外界对该对象的访问,都必须先通过这层拦截,因此提供了一种机制,可以对外界的访问进行过滤和改写。Proxy 这个词的原意是代理,用在这里表示由它来 “代理…...

verilog实现一个5bit序列检测器
以下是用 Verilog 实现一个 5bit 序列检测器的代码: module five_bit_sequence_detector(input clk,input reset,input [4:0] in,output reg detected );// 定义状态参数localparam IDLE 4b0000;localparam STATE1 4b0001;localparam STATE2 4b0010;localparam …...

Redis数据安全_持久化机制
由于Redis的数据都存放在内存中,如果没有配置持久化,Redis重启后数据就全丢失了,于是需要开启Redis的持久化功能,将数据保存到磁盘上,当Redis重启后,可以从磁盘中恢复数据。 持久化机制概述 对于Redis而言…...

什么是信息熵,什么是交叉熵,什么是KL散度?
什么是信息熵? 信息熵(Entropy)是信息论中的一个基本概念,用来衡量一个随机变量不确定性的大小。它反映了对一个事件结果的预测难度,或者说是描述这个事件需要多少“信息量”。信息熵是由香农(Claude Shan…...
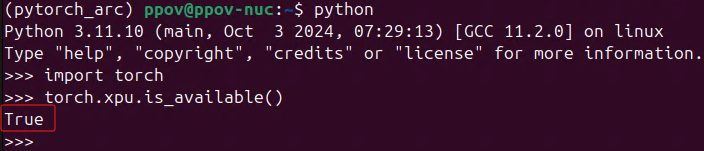
开发者的福音:PyTorch 2.5现已支持英特尔独立显卡训练
《PyTorch 2.5重磅更新:性能优化新特性》中的一个新特性就是:正式支持在英特尔独立显卡上训练模型! PyTorch 2.5 独立显卡类型 支持的操作系统 Intel 数据中心GPU Max系列 Linux Intel Arc™系列 Linux/Windows 本文将在IntelCore™…...

Deep InfoMax(DIM)(2019-02-ICLR)
论文:LEARNING DEEP REPRESENTATIONS BY MUTUAL INFORMATION ESTIMATION AND MAXIMIZATION ABSTRACT 研究目标 研究通过最大化输入和深度神经网络编码器输出之间的互信息来进行无监督表示学习目的是学习到对下游任务有用的特征表示 核心发现:结构很重…...

2024年10月中国数据库排行榜:TiDB续探花,GaussDB升四强
10月中国数据库流行度排行榜如期发布,再次印证了市场分层的加速形成。国家数据库测评结果已然揭晓,本批次通过的产品数量有限,凸显了行业标准的严格与技术门槛的提升。再看排行榜,得分差距明显增大,第三名与后续竞争者…...

css边框修饰
一、设置线条样式 通过 border-style 属性设置,可选择的一些属性如下: dotted:点线 dashed:虚线 solid:实线 double:双实线 效果如下: 二、设置边框线宽度 ① 通过 border-width 整体设置…...

利用Python进行数据可视化:实用指南与推荐库
利用Python进行数据可视化:实用指南与推荐库 数据可视化是将数据转化为图形和图表的过程,它能够帮助我们更直观地理解数据的趋势、模式和关系。在Python中,有许多强大的库可用于数据可视化,从简单的折线图到复杂的交互式图表,应有尽有。本文将详细介绍Python数据可视化的…...

MobileNetv2网络详解
背景: MobileNet v1中DW卷积在训练完之后部分卷积核会废掉,大部分参数为“0” MobileNet v2网络是由Google团队在2018年提出的,相比于MobileNet v1网络,准确率更高,模型更小 网络亮点: Inverted Residu…...

惊了!大模型连这样的验证码都能读懂_java_识别验证码
最近在看视觉大模型的能力,然后用了某网站的一个验证码试了试,竟然连这样的验证码都能认识,这个有点夸张,尤其是这个9和6颠倒的都能理解,现在的能力已经这么牛了么 具体就是用了通义最新的qwen vl模型spring ai alibab…...
【小白学机器学习26】 极大似然估计,K2检验,logit逻辑回归(对数回归)(未完成----)
目录 1 先从一个例题出来,预期值和现实值的差异怎么评价? 1.1 这样一个问题 1.2 我们的一般分析 1.3 用到的关键点1 1.4 但是差距多远,算是远呢? 2 极大似然估计 2.1 极大似然估计的目的 2.1.1 极大似然估计要解决什么问题…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
