当前位置： 首页 > news >正文

telnet 密码模式 访问路由器

news 2026/2/8 10:55:20

telnet 密码访问华为路由器

在这里插入图片描述
模拟被访问路由
sy
[Huawei]int g0/0/0 //选中 g0/0/0端口
[Huawei-GigabitEthernet0/0/0]ip add 192.168.1.1 24 //设置端口ip

[Huawei]user-interface vty 0 4 //配置vty
[Huawei-ui-vty0-4]set authentication password cipher huawei@123 //设置vty 明文密码 huawei@123
[Huawei-ui-vty0-4]user privilege level 15 //设置vty用户级别15
在这里插入图片描述

模拟pc
sy
[Huawei]int g0/0/0 //选中g0/0/0端口
[Huawei-GigabitEthernet0/0/0]ip add 192.168.1.2 24 //设置端口ip

[Huawei-GigabitEthernet0/0/0]q
[Huawei]q
telnet 192.168.1.1 //用户模式下访问192.168.1.1
Press CTRL_] to quit telnet mode
Trying 192.168.1.1 …
Connected to 192.168.1.1 …

Login authentication

Password:

相关文章：

telnet 密码模式 访问路由器

telnet 密码访问华为路由器 模拟被访问路由 sy [Huawei]int g0/0/0 //选中 g0/0/0端口 [Huawei-GigabitEthernet0/0/0]ip add 192.168.1.1 24 //设置端口ip [Huawei]user-interface vty 0 4 //配置vty [Huawei-ui-vty0-4]set authentication password cipher huawei123 //设置…...

编程日记 2024/10/30 18:13:58

文心一言 VS 讯飞星火 VS chatgpt （380）-- 算法导论24.4 12题

十二、给出一个有效算法来解决 A x ⩽ b Ax⩽b Ax⩽b 的差分约束系统，这里 b b b 的所有元素为实数，而变量 x i x_i xi​ 中某个给定的子集是整数。如果要写代码，请用go语言。 文心一言： 差分约束系统问题通常用于解决带有约…...

编程日记 2024/10/30 18:12:57

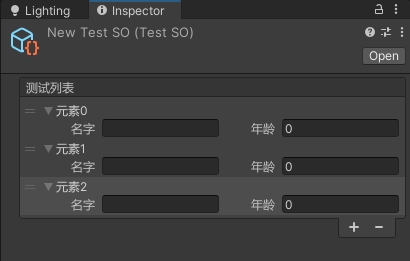
Unity自定义数组在Inspector窗口的显示方式

了解 单行高度:EditorGUIUtility.singleLineHeight获取 PropertyField 控件所需的高度:EditorGUI.GetPropertyHeight属性是否在Inspector窗口展开：SerializedProperty.isExpanded可重新排序列表类：ReorderableList绘制纯色矩形：EditorGUI.Dr…...

编程日记 2024/10/30 18:10:55

ERC论文阅读(03)--SPCL论文阅读笔记(2024-10-29)

SPCL论文阅读笔记 论文中心思想 这篇论文是研究ERC任务的论文，作者提出了监督原型对比学习的方法用于ERC任务。 论文 EMNLP2022 paper “Supervised Prototypical Contrastive Learning for Emotion Recognition in Conversation” 现存问题 现存的使用监督对…...

编程日记 2024/10/30 18:08:53

Straightforward Layer-wise Pruning for More Efficient Visual Adaptation

对于模型中冗余的参数，一个常见的方法是通过结构化剪枝方法减少参数容量。例如，基于幅度值和基于梯度的剪枝方法。尽管这些方法在传统训练上通用性，本文关注的PETL迁移有两个不可避免的问题： 显著增加了模型存储负担。由于不同的…...

编程日记 2024/10/30 18:07:52

喜讯 | 创邻科技杭州电子科技大学联合实验室揭牌成立！

近日，杭州电子科技大学图书情报专业硕士行业导师聘任仪式暨杭电-创邻图技术与数字化联合实验室（图书档案文物数字云联合研发中心）揭牌仪式在杭州电子科技大学隆重举行。杭州电子科技大学原副校长吕金海、研究生院副院长潘建江，科研…...

编程日记 2024/10/30 18:05:50

海外媒体发稿：如何打造媒体发稿策略

新闻媒体的发稿推广策略对于提升品牌知名度、吸引流量以及增加收入非常重要。本文将介绍一套在21天内打造爆款新闻媒体发稿推广策略的方法。 第一天至第七天：明确目标和定位 在这个阶段，你需要明确你的目标和定位，以便为你的新闻媒体建立一个…...

编程日记 2024/10/30 18:03:48

PyTorch模型保存与加载

1.保存与加载的概念（序列化与反序列化） 模型训练完毕之后，肯定想要把它保存下来，供以后使用，不需要再次去训练。 那么在pytorch中如何把训练好的模型，保存，保存之后又如何加载呢？ 这就用需要序列化与反序列化，序列化与反序列化的概念如下图所示： 因为在内…...

编程日记 2024/10/30 18:02:47

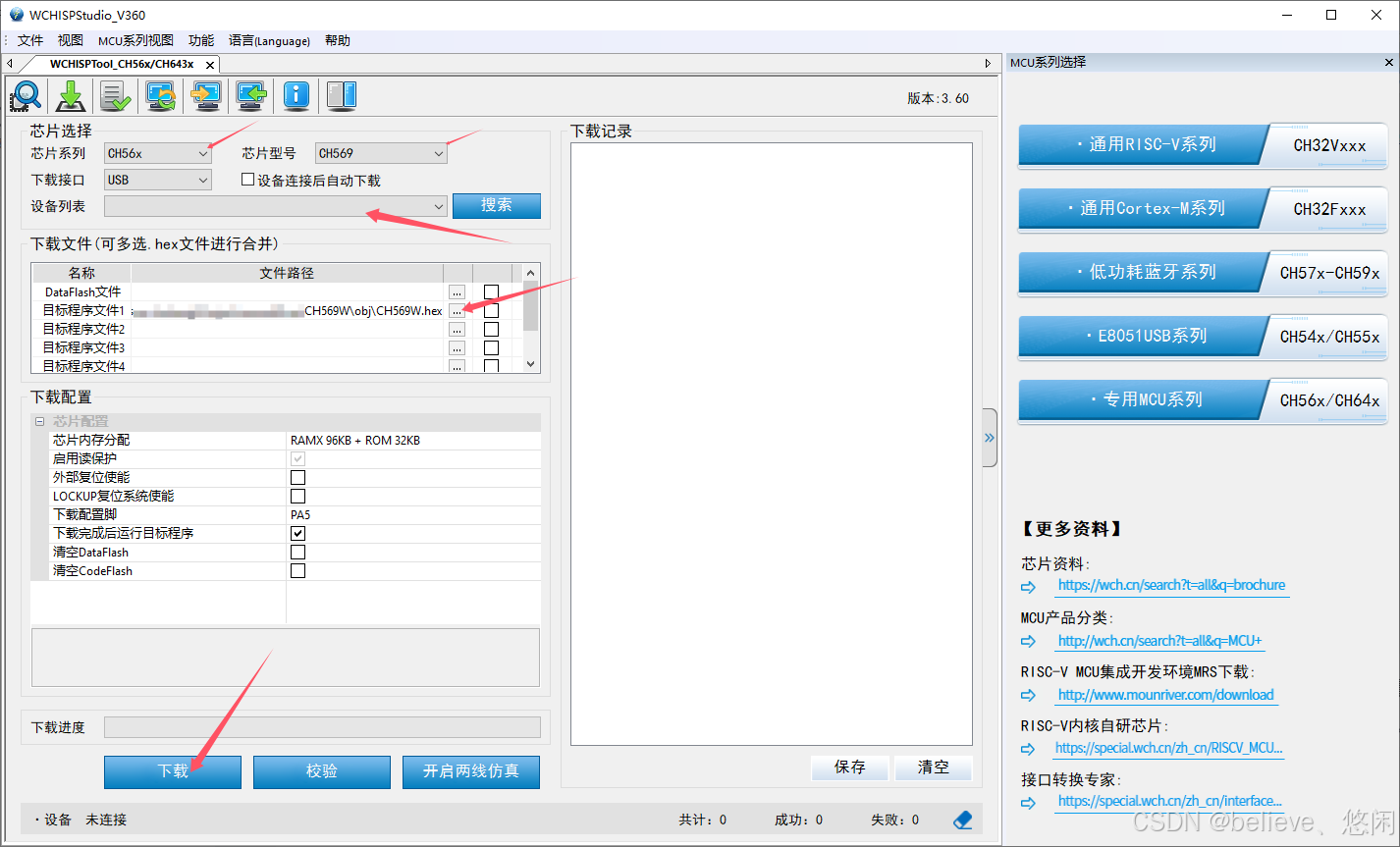
CH569开发前的测试

为了玩转准备Ch569的开发工作 ，准备了如下硬件和软件： 硬件 1.官方的 Ch569 开发板，官方买到的是两块插接在一起的；除了HSPI接口那里的电阻，这两块可以说是一样的。也意味着两块板子的开发也需要烧录两次&#xff1b…...

编程日记 2024/10/30 18:00:43

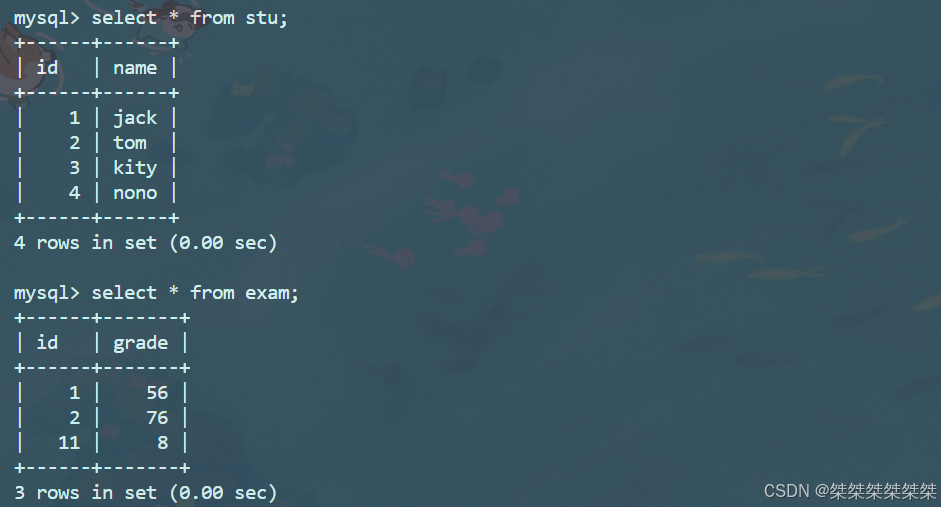
MySQL中表的外连接和内连接

内连接和外连接 ​ 表的连接分为内连接和外连接，内连接就是将需要连接的表形成笛卡尔积筛选；外连接分为左外连接和右外连接，左外连接为左侧的表需要完全显示，右外连接为右侧的表现需要完全显示。 文章目录 内连接和外连接内连接外…...

编程日记 2024/10/30 17:59:42

Ubuntu 上安装 Redmine 5.1 指南

文章目录 官网安装文档：命令步骤相关介绍GemRubyRailsBundler 安装 Redmine更新系统包列表和软件包：安装必要的依赖：安装 Ruby：安装 bundler下载 Redmine 源代码：安装 MySQL配置 Redmine 的数据库配置文件：…...

编程日记 2024/10/30 17:58:41

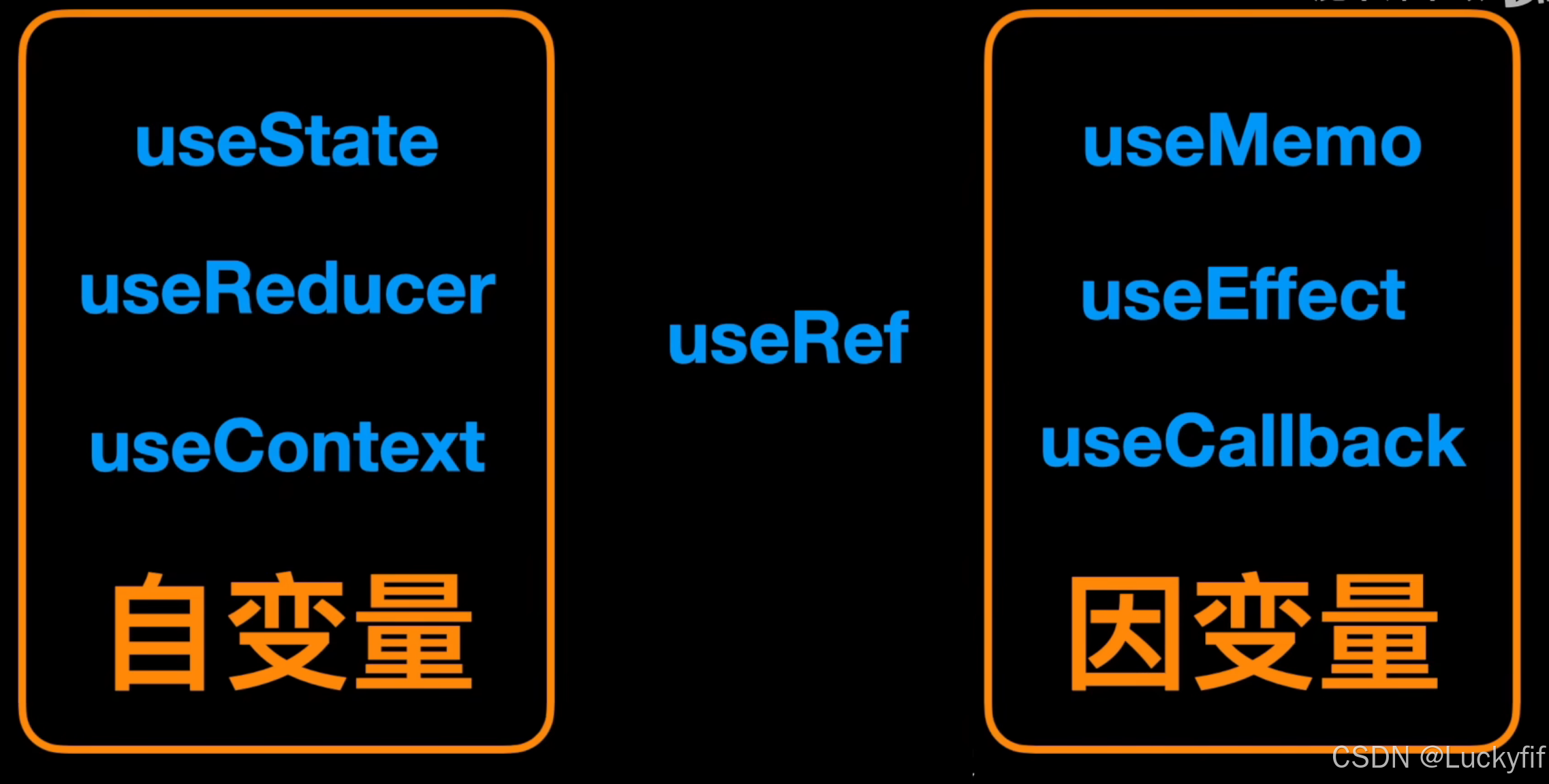
从变量的角度理解 Hooks , 变得更简单了

从变量角度理解Hooks 在React的世界里，Hooks的引入为函数式组件带来了前所未有的灵活性和能力。它们让我们得以完全摆脱class式的写法，在函数式组件中完成生命周期管理、状态管理、逻辑复用等几乎全部组件开发工作。这次，我们就从变量的角度…...

编程日记 2024/10/30 17:56:39

LabVIEW Modbus通讯稳定性提升

在LabVIEW开发Modbus通讯程序时，通讯不稳定是一个常见问题，可能导致数据丢失、延迟或错误。为了确保通讯的可靠性，可以从多个角度进行优化，以下是一些有效的解决方案，结合实际案例进行分析。 1. 优化通讯参数设置 通讯…...

编程日记 2024/10/30 17:55:38

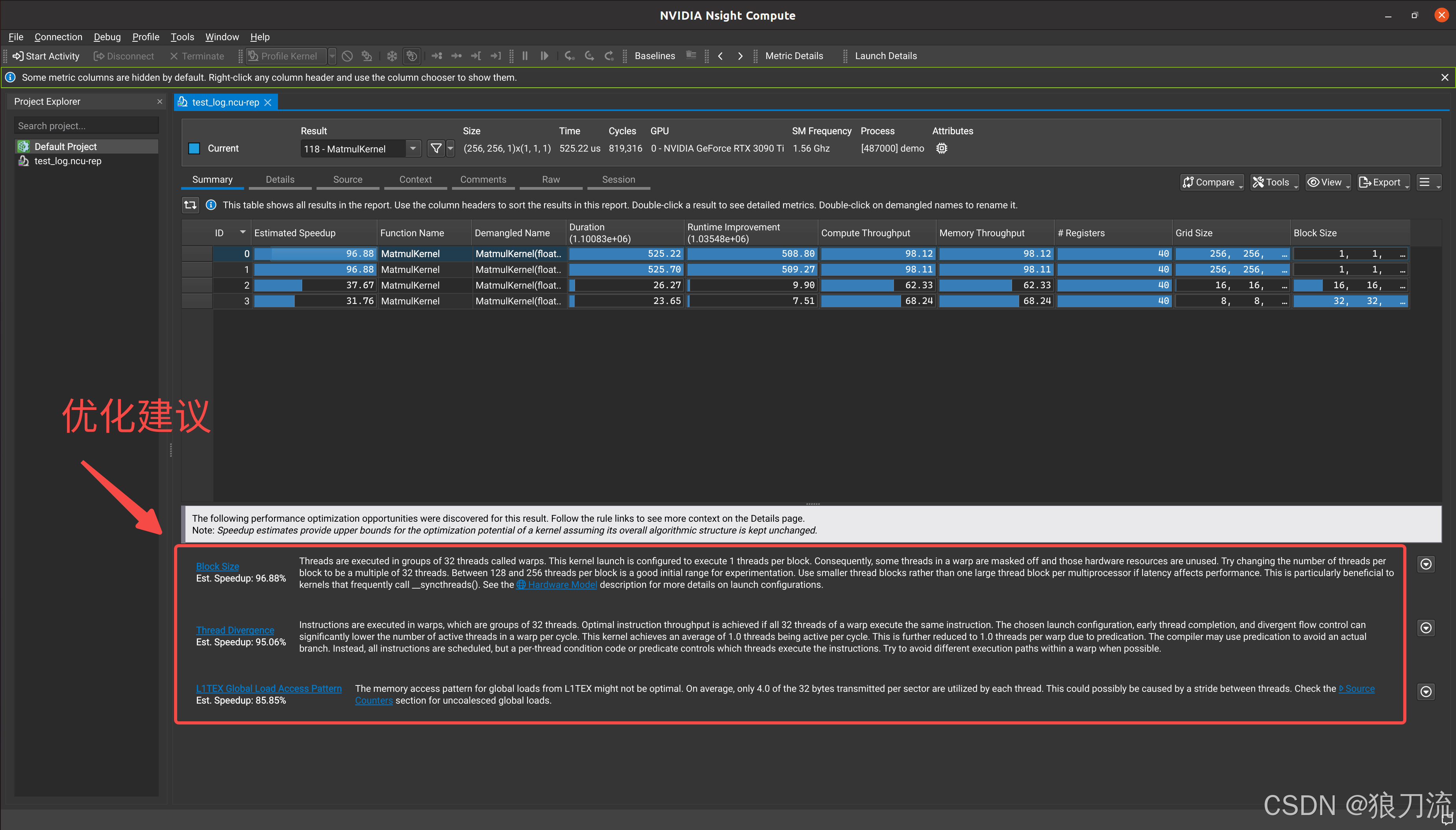
(8) cuda分析工具

文章目录 Nvidia GPU性能分析工具Nsight SystemNvidia GPU性能分析工具Nsight System Nvidia GPU性能分析工具Nsight System NVIDIA Nsight Systems是一个系统级的性能分析工具，用于分析和优化整个CUDA应用程序或系统的性能。它可以提供对应用程序整体性能的全面见…...

编程日记 2024/10/30 17:53:36

C语言 | Leetcode C语言题解之第517题超级洗衣机

题目&#xff1a; 题解&#xff1a; int findMinMoves(int* machines, int machinesSize){int sum0;for(int i0;i<machinesSize;i){summachines[i];}if(sum%machinesSize!0){return -1;}int psum/machinesSize;int ans0;int cur0;for(int i0;i<machinesSize;i){cur(mac…...

编程日记 2024/10/30 17:52:35

Java多线程编程基础

目录 编写第一个多线程程序 1. 方式一 : 继承Thread类, 重写run方法 2. 方式二: 实现Runnable接口, 重写run方法 3. 方式三: 使用Lambda表达式 [匿名内部类] [Lambda表达式] 在上个文章中, 我们了解了进程和线程的相关概念. 那么, 在Java中, 我们如何进行多线程编程呢? …...

编程日记 2024/10/30 17:50:33

刷代随有感(134):单调栈——下一个更大元素I（难点涉及哈希表与单调栈的结合)

单调栈处理的是下标&#xff01; 题干&#xff1a; 代码&#xff1a; class Solution { public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {stack<int>ddst;unordered_map<int,int>umap;vector<int…...

编程日记 2024/10/30 17:40:22

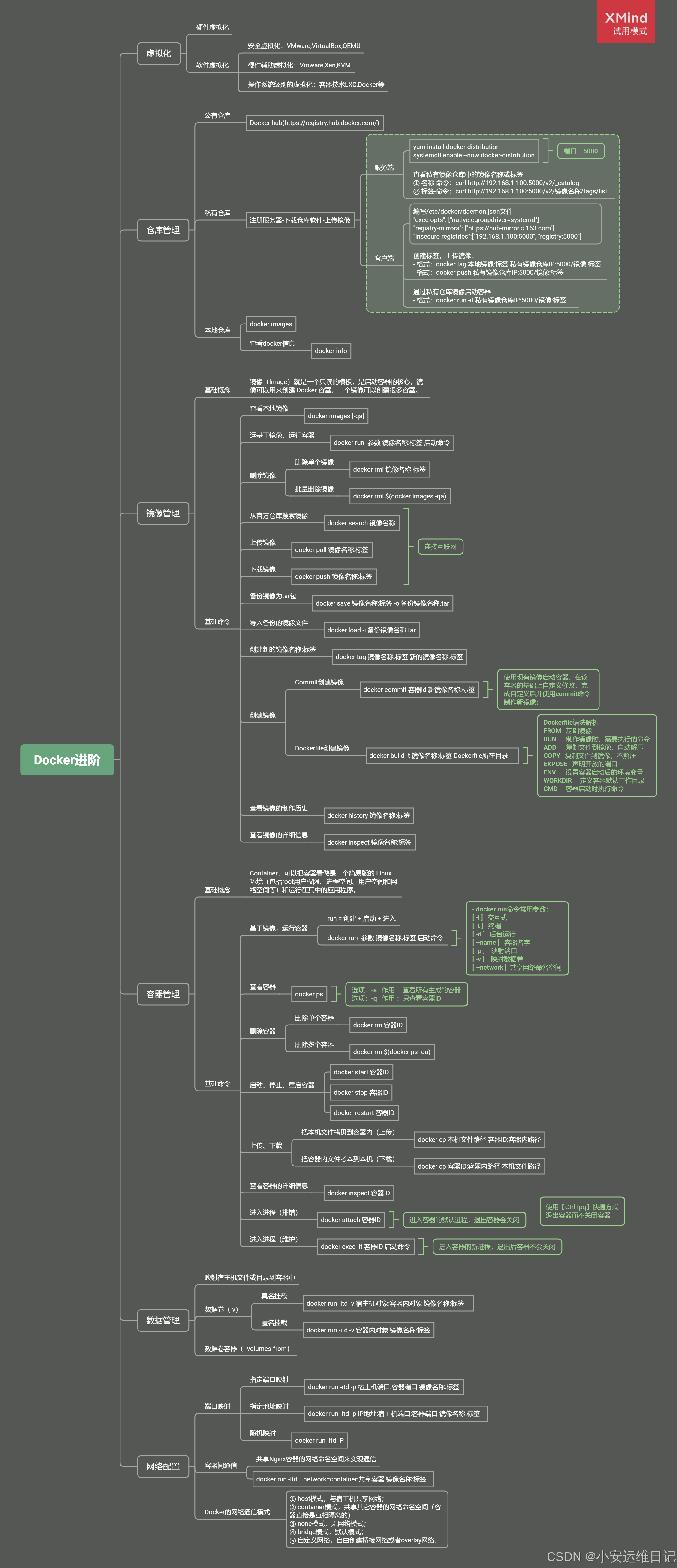
Linux云计算 |【第五阶段】CLOUD-DAY5

主要内容&#xff1a; 容器的镜像编排&#xff0c;commit简单镜像创建&#xff0c;Dockerfile制作服务镜像&#xff08;语法、创建镜像&#xff09;、创建复杂镜像&#xff08;Docker微服务架构、示例&#xff1a;NGINXPHP&#xff09;、私有仓库 一、简单镜像创建 1、自定义…...

编程日记 2024/10/30 17:37:19

被上传文件于后端的命名策略

上一篇博客我们了解了前端上传的文件资源应该存放在后端项目中的什么位置&#xff0c;那么随之而来的另一个问题——我们应该如何为上传的文件命名呢&#xff1f;往往直接采用原文件名并不稳妥&#xff0c;会导致命名冲突、文件冲突、数据库管理冲突等多种问题&#xff0c;下面…...

编程日记 2024/10/30 17:35:17

哈希表 算法专题

哈希表简介 是什么 存储数据的容器有啥用? "快速"查找某个元素什么时候用哈希表 频繁地查找某个数(有序用二分)怎么用哈希表 容器用数组模拟 字符串中的字符 范围比较小的数 一. 两数之和 两数之和 class Solution {public int[] twoSum(int[] nums, int targe…...

编程日记 2024/10/30 17:34:15

观成科技：隐蔽隧道工具Ligolo-ng加密流量分析

1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具&#xff0c;该工具基于TUN接口实现其功能&#xff0c;利用反向TCP/TLS连接建立一条隐蔽的通信信道&#xff0c;支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式&#xff0c;适应复杂网…...

编程新知 2026/2/8 4:37:24

Flask RESTful 示例

目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题&#xff1a; 下面创建一个简单的Flask RESTful API示例。首先&#xff0c;我们需要创建环境&#xff0c;安装必要的依赖&#xff0c;然后…...

编程新知 2026/2/6 3:59:37

STM32标准库-DMA直接存储器存取

文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA&#xff08;Direct Memory Access&#xff09;直接存储器存取 DMA可以提供外设…...

编程新知 2026/1/26 10:55:51

智能仓储的未来：自动化、AI与数据分析如何重塑物流中心

当仓库学会“思考”&#xff0c;物流的终极形态正在诞生 想象这样的场景&#xff1a; 凌晨3点&#xff0c;某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径&#xff1b;AI视觉系统在0.1秒内扫描包裹信息&#xff1b;数字孪生平台正模拟次日峰值流量压力…...

编程新知 2026/2/1 2:49:30

大学生职业发展与就业创业指导教学评价

这里是引用 作为软工2203/2204班的学生&#xff0c;我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要&#xff0c;而您认真负责的教学态度&#xff0c;让课程的每一部分都充满了实用价值。 尤其让我…...

编程新知 2025/11/16 1:39:27

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/12/2 3:35:50

Swagger和OpenApi的前世今生

Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章&#xff0c;二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑&#xff1a; &#x1f504; 一、起源与初创期&#xff1a;Swagger的诞生&#xff08;2010-2014&#xff09; 核心…...

编程新知 2026/1/25 9:08:41

Unsafe Fileupload篇补充-木马的详细教程与木马分享（中国蚁剑方式）

在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马&#xff08;服务器方面的&#xff09;的原理&#xff0c;连接&#xff0c;以及各种木马及连接工具的分享 文件木马&#xff1a;https://w…...

编程新知 2026/1/25 10:13:29

现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？

现有的 Redis 分布式锁库&#xff08;如 Redisson&#xff09;相比于开发者自己基于 Redis 命令&#xff08;如 SETNX, EXPIRE, DEL&#xff09;手动实现分布式锁&#xff0c;提供了巨大的便利性和健壮性。主要体现在以下几个方面&#xff1a; 原子性保证 (Atomicity)&#xff…...

编程新知 2025/9/23 11:26:04

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00