ReactOS系统中平衡二叉树。给定地址超导其所属区块MmFindRegion()
系列文章目录
PMM_REGION NTAPI MmFindRegion(
PVOID BaseAddress,
PLIST_ENTRY RegionListHead,
PVOID Address,
PVOID* RegionBaseAddress
);
宏函数
//给定地址找到其中所属区块
#define CONTAINING_RECORD(address,type,field) ((type FAR *\(PCHAR)(address)-(PCHAR)(&((type *)0)->field)))获取外层数据结构的指针```
@[TOC](文章目录)---# MmFindRegion()
```c
//给定地址超导其所属区块
PMM_REGION NTAPI
MmFindRegion(PVOID BaseAddress, PLIST_ENTRY RegionListHead,PVOID Address, PVOID * RegionBaseAddress)
{PLIST_ENTRY current_entry;PMM_REGION current;PVOID StartAddress = BaseAddress;//搜索的起点current_entry = RegionListHead->Flink;//获得第一个MM REGION区块指针while (current_entry != RegionListHead)//遍历一个MEMORY AREA即某个区间的区块双向链表{//curren获得该指向该结构的首地址current = CONTAINING_RECORD(current entry, MM REGION, RegionListEntry);//若目标地址在(StartAddress ~startAddress+current->Length)说明找到了该地址所在区块if (StartAddress <= Address &&((char*)StartAddresS + current->Length) > (char*)Address) {//找到了if (RegionBaseAddress != NULL)*RegionBaseAddress = StartAddress;//将区块开始地址给RegionBaseAddress返回return(current);//返回该区块的结构信息currententry = current_entry->Flink://下一个区块StartAddress =(PVOID)((ULONG PTR)StartAddress + current->Length);return(NULL);}current_entry = current_entry->Flink;//下一个区块StartAddress = (PVOID)((ULONG_PTR)StartAddress + current->Length);}return (NULL);
}
c
相关文章:
)
ReactOS系统中平衡二叉树。给定地址超导其所属区块MmFindRegion()
系列文章目录 PMM_REGION NTAPI MmFindRegion( PVOID BaseAddress, PLIST_ENTRY RegionListHead, PVOID Address, PVOID* RegionBaseAddress ); 宏函数 //给定地址找到其中所属区块 #define CONTAINING_RECORD(address,type,field) ((type FAR *\(PCHAR)(address)-(PCHAR)(&…...

基于TESSY的单元测试与分类树方法深入解析
在现代软件开发中,单元测试是确保软件质量和可靠性的关键步骤之一。特别是对于嵌入式软件,由于其应用环境的特殊性和高安全性要求,单元测试显得尤为重要。本文将基于《TESSY 用户手册》的内容,详细介绍如何使用TESSY 进行单元测试,并深入探讨分类树方法(Classification T…...

整理了一些大模型的课程,非常详细,大模型零基础入门到精通,收藏我这一篇就够了
目前有多个科普类的大模型课程,这些课程涵盖了从基础理论到实际应用的各个方面。以下是一些主要的科普类大模型课程:复旦大学“大模型开发与赋能”专题讲习班:由复旦大学计算机学院邱锡鹏教授带来的《大模型科普讲解》课程,通过深…...

区块链国赛题目--食品溯源(模块三)
区块链国赛题目–食品溯源(模块三) 任务 3-1:区块链应用前端功能开发 1.请基于前端系统的开发模板,在登录组件 login.js、组件管理文件components.js 中添加对应的逻辑代码,实现对前端的角色选择功能,并测试功 能完整性,示例页面如下: 具体要求如下: (1)有明…...

【Searxng】Searxng docker 安装
SearXNG将用户的查询请求分发至多个支持的搜索引擎,并收集返回的结果进行汇总处理。在这个过程中,它通过内置的过滤器功能屏蔽广告和其他不相关内容,确保搜索结果的纯净度。 一键部署 docker run \--name searxng \-p ????:8080 \-v ~/s…...

Java Lock/AQS ReentrantLock 源码
前言 相关系列 《Java & Lock & 目录》(持续更新)《Java & AQS & 目录》(持续更新)《Java & Lock/AQS & ReentrantLock & 源码》(学习过程/多有漏误/仅作参考/不再更新)《Jav…...

魔法伤害--是谁偷走了我的0
起因:需要迁移数据进行数据更新,使用pandasorcal进行数据处理以及库迁移 首先把数据导出为xls格式数据文件,使用python import pandas as pdnew_obj pd.read_excel(ne,dtype{DAY: str, MONTH: str}) 原有导出数据格式为: 使用…...

【ArcGIS Pro实操第4期】绘制三维地图
【ArcGIS Pro实操第4期】绘制三维地图 ArcGIS Pro绘制三维地图-以DEM高程为例参考 如何使用ArcGIS Pro将栅格数据用三维的形式进行表达?在ArcGIS里可以使用ArcScene来实现,ArcGIS Pro实现原理跟ArcScene一致。由于Esri未来将不再对ArcGIS更新,…...

Vuestic 整理使用
简单示例 1. 条件渲染 2. 列表渲染 3. 组件插槽 4. 插值语法 5. 前后端路由的区别(还是转一下,可以减少代码量)SFC 构建 … … Okay,可以干活了,通顺 数据表的操作更加简化了 数据类别通过后端路由区别,但是还得由前端路由转一下 简单了许多呀,上脚手…...

学习伊圣雨老师的 epoll 编程
(1)书里提出了疑问,epoll 函数的工作方式,区分为水平触发与边缘触发 : (2) 谢谢...

详细了解C++11(1)
大家好呀,我是残念,希望在你看完之后,能对你有所帮助,有什么不足请指正!共同学习交流哦 本文由:残念ing原创CSDN首发,如需要转载请通知 个人主页:残念ing-CSDN博客,欢迎各…...

ITA的去锅盖处理流程
一、说明 锅盖是什么 锅盖的类型有哪些 二、去锅盖处理流程 去锅盖算法首先需要采集一份锅盖模板数据,该模板数据用户可以自定义保存,方便后面的开机重启直接导入使用。去锅盖处理包含两个历程:保存锅盖模板;去锅盖处理。 保存锅盖模板: ( 1 ) 打开采集锅盖模板开关。…...

日志管理系统的系统目标是什么?
在网络安全、数据管理、故障排查等领域,日志都被广泛使用并需要进行有效的管理与分析。因此,日志管理系统的系统目标显得尤为重要,如以下几方面。 1、确保数据的安全性及完整性 在企业和组织的日常运营中,各类信息数据都会通过系统…...

uniapp 底部导航栏tabBar设置后不显示的问题——已解决
uniapp 底部导航栏tabBar设置后不显示的问题——已解决 网上找了一堆解决办法,挨个对着试吧 解决办法一:tabBar里的list第一项和page中的第一项要相同,确实就能显示了。但是问题来了,page中的第一项是入口页,那就意味…...

JVM 类加载器
字节码的结构 魔数u4 cafe babe 版本u4 52 java8 常量池计数器u2 从1开始,0索引留给不需要的情况 常量池 表 #1 -> #计数器-1 类标识符 u2 public final abstrat class annotion interface 之类 类索引u2 名字 父类索引u2 父类名字 接口计数器 u2 接口数…...

《C++长时间运行程序:驯服内存膨胀的“怪兽”》
在 C编程的世界里,当我们编写长时间运行的程序时,内存膨胀问题就像一个隐藏在暗处的“怪兽”,随时可能吞噬我们程序的性能和稳定性。无论是服务器应用程序、大型模拟系统还是其他长时间运行的关键任务软件,有效地处理内存膨胀问题…...

ELK之路第二步——可视化界面Kibana
Kibana 1.安装2.解压3.修改配置4.启动 这部分内容就比较简单了,水一片文章。 1.安装 需要梯子 官网下载链接:https://www.elastic.co/cn/downloads/past-releases/kibana-7-3-0 如果你去官网下载页面,点击下载是404报错,记得切换…...
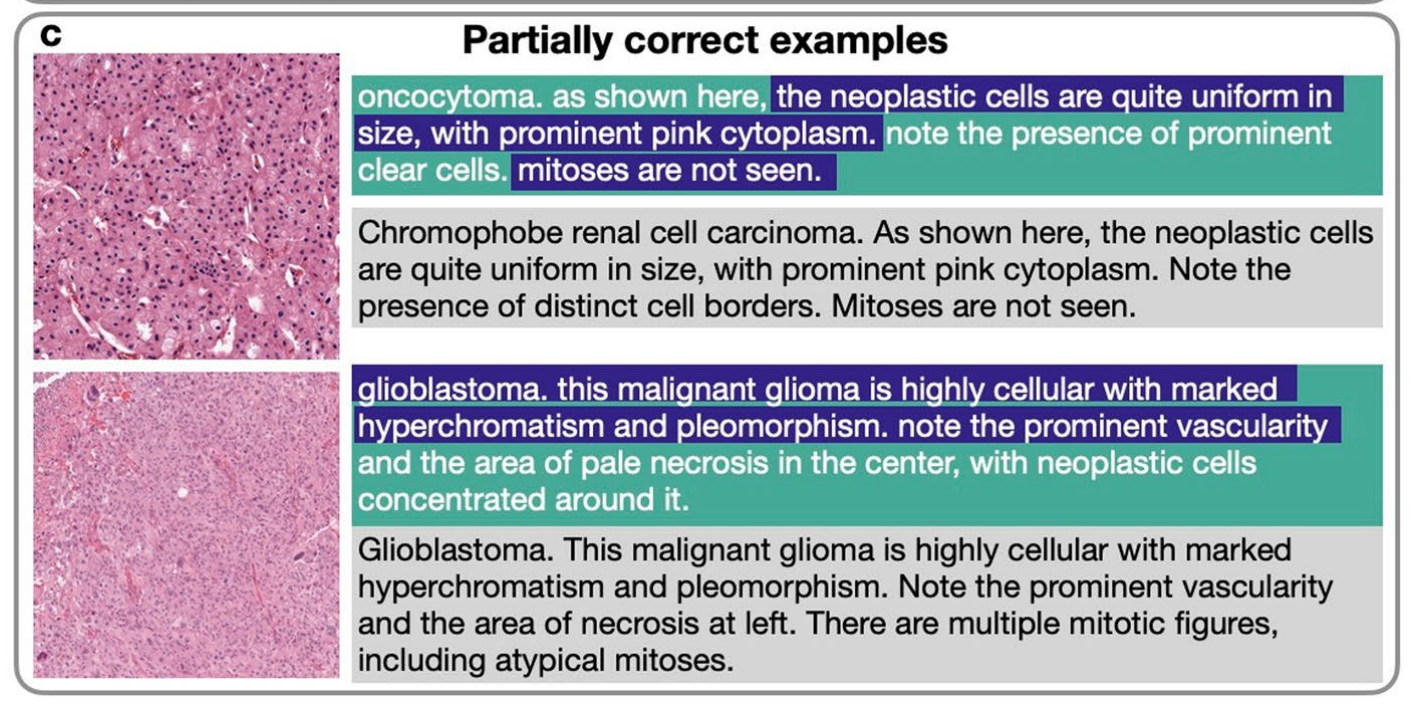
Nature Medicine病理AI汇总|CONCH:病理图像分析的零样本学习模型·顶刊精析·24-10-30
小罗碎碎念 最近在整理24年发表在Nature Medicine上的病理AI文章,简单列了一个表。 接下来我将按照先后顺序,系统的把这13篇文献分析完。其中底色做了填充的,代表商业公司在本论文中占据了一作或通讯。 本期推文介绍的模型是CONCH࿰…...

通过不当变更导致 PostgreSQL 翻车的案例分析与防范
在数据库管理领域,PostgreSQL 凭借其强大的功能和稳定性,赢得了广泛的认可。然而,即便是如此稳健的系统,在不当的变更操作下,也可能遭遇性能下降、数据丢失甚至系统崩溃的风险。本文将通过一个具体案例,分析…...

Windows高级技巧:轻松实现多进程窗口的连接与管理
在Windows操作系统中,管理多个进程窗口可能是一项复杂的任务,特别是在自动化测试或多任务处理时。本文将介绍一种高效的方法,通过Python编程和AirtestIDE工具,实现多进程窗口的便捷连接与管理。同时,将提供具体的代码示…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
