两步GMM计算权重矩阵
在广义矩方法(GMM)中,权重矩阵(W)的选择是关键的一步。理想情况下,(W)应该等于矩条件的协方差矩阵的逆矩阵。这是因为使用这样的权重矩阵可以使得估计量达到最小方差,从而提高估计效率。
两步GMM计算权重矩阵(W)
-
第一步 - 初始估计:
- 使用一个简单的权重矩阵(如单位矩阵)来进行初始的参数估计。
- 基于这个初始估计,计算出样本矩条件向量(g_n(\theta))。
-
估计协方差矩阵:
- 使用初始估计得到的参数值来计算每个观测点的矩条件向量(g(x_i, \hat{\theta}_0))。
- 计算这些矩条件向量的样本协方差矩阵(\hat{S})。
-
构造新的权重矩阵:
- 将上述估计得到的协方差矩阵取逆,即得到更有效的权重矩阵(\hat{W} = \hat{S}^{-1})。
MATLAB代码示例
下面是一个MATLAB代码示例,演示如何通过两步GMM来计算权重矩阵(W):
% 生成模拟数据
n = 1000; % 样本数量
x = randn(n, 1); % 自变量
e = randn(n, 1); % 随机扰动项
y = 1 + 2 * x + e; % 因变量,真实参数为β0=1, β1=2% 定义矩条件函数
moment_conditions = @(params, x, y) [y - (params(1) + params(2) * x), ...x .* (y - (params(1) + params(2) * x))];% 第一步:使用单位矩阵作为初始权重矩阵进行初始估计
W_initial = eye(2);
options = optimset('Display', 'iter', 'MaxIter', 500, 'TolX', 1e-8, 'TolFun', 1e-8);
objective_function = @(params, x, y, W) moment_conditions(params, x, y)' * W * moment_conditions(params, x, y);
start_params = [0, 0];
result_initial = fminunc(@(params) objective_function(params, x, y, W_initial), start_params, options);% 第二步:基于初始估计计算新的权重矩阵
g_n = moment_conditions(result_initial, x, y);
S_hat = g_n' * g_n / n; % 估计协方差矩阵
W_new = inv(S_hat); % 新的权重矩阵% 输出新的权重矩阵
disp('New Weight Matrix W:');
disp(W_new);% 可以继续使用新的权重矩阵W_new进行第二次优化
result_final = fminunc(@(params) objective_function(params, x, y, W_new), result_initial, options);% 输出最终结果
fprintf('Final estimated parameters: beta0 = %.4f, beta1 = %.4f\n', result_final(1), result_final(2));
代码解释
- 生成数据:生成模拟数据。
- 定义矩条件:定义矩条件函数
moment_conditions。 - 第一步 - 初始估计:使用单位矩阵作为初始权重矩阵,通过
fminunc进行初始参数估计。 - 第二步 - 估计协方差矩阵:基于初始估计,计算每个观测点的矩条件向量,并估计协方差矩阵(\hat{S})。
- 构造新的权重矩阵:将协方差矩阵取逆,得到新的权重矩阵(\hat{W})。
- 输出新的权重矩阵:显示新的权重矩阵。
- 第二次优化:使用新的权重矩阵进行第二次优化,得到最终的参数估计。
这个过程展示了如何通过两步GMM来计算和更新权重矩阵。你可以根据具体问题调整矩条件、数据处理和优化选项。如果你有更具体的模型或数据,请提供更多细节以便进一步定制化处理。
相关文章:

两步GMM计算权重矩阵
在广义矩方法(GMM)中,权重矩阵(W)的选择是关键的一步。理想情况下,(W)应该等于矩条件的协方差矩阵的逆矩阵。这是因为使用这样的权重矩阵可以使得估计量达到最小方差,从而提高估计效率。 两步GMM计算权重矩阵(W) 第一…...

leetcode452. 用最少数量的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。 一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一…...

【Android】使用TextView实现按钮开关代替Switch开关
介绍 Android 本身自己带的有开关控件,但是很多时候我们是不愿意使用这种开关的,感觉使用起来比较麻烦,特别是遇到需要延迟操作的情况。 比如有一个需求是这样的:我们需要打开一个设置,但是这个设置是否打开需要经过…...

(49)MATLAB实现迫零均衡器原理与代码
文章目录 前言一、迫零均衡器设计说明二、迫零均衡器MATLAB源代码1.函数说明2.代码实现3.辅助函数 前言 使用MATLAB实现迫零均衡器。给出完整的MATLAB设计源代码。 一、迫零均衡器设计说明 理想的迫零均衡器有无限多个抽头权系数,是不能实现的,本文考虑…...

滚柱导轨出现异常损坏的原因
滚柱导轨是一种精密的直线滚动导轨,具有较高的承载能力和较高的刚性,对反复动作、起动、停止往复运动频率较高情况下可减少整机重量和传动机构及动力成本。滚柱导轨可获得较高的灵敏度和高性能的平面直线运动,在重载或变载的情况下࿰…...
论文专题:论分布式架构设计)
架构师考试系列(6)论文专题:论分布式架构设计
论分布式架构设计 摘要: 2020年2月,我司中标了某省电力公司的配网运维管控项目,该项目接入电力公司营销、设备和调度等多个部门的专业数据,为配网运行、配网检修、配网抢修、配网工程、供电服务等核心业务提供数据支撑。由于本项目是省级项目,系统可靠性、可用性要求比较…...

leetcode hot100【LeetCode 230. 二叉搜索树中第K小的元素】java实现
LeetCode 230. 二叉搜索树中第K小的元素 题目描述 给定一个二叉搜索树的根节点 root,和一个整数 k,请你找出其中第 k 小的节点。 注意: 题目保证 k 的有效性。 示例: 给定二叉搜索树: 5/ \3 7/ \ \ 2 4 …...

从0开始深度学习(23)——图像卷积
上节了解了卷积层的原理,本节以图像为例,介绍一下它的实际应用 1 互相关运算 严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation)。 首先,我们暂时忽略通…...

编程小白如何成为大神
成为编程大神的过程需要时间、耐心和实践。以下是一些适合大学新生的入门攻略: 1. 确定学习目标 选择语言:选择一门编程语言作为起点,如 Python、Java 或 JavaScript。Python 是初学者的热门选择,因为其语法简洁易懂。设定目标&…...

JetCache启动循环依赖分析
问题呈现 项目性能优化,需要将本地内存(JVM内存)替换为本地Redis(同一个Pod中的Container),降低JVM内存和GC的压力,同时引入了JetCache简化和统一使用(对JetCache也做了扩展&#x…...
【科研绘图】3DMAX管状图表生成插件TubeChart使用方法
3DMAX管状图表生成插件TubeChart,一款用于制作3D管状图表的工具。可以自定义切片的数量以及随机或指定切片颜色。 【版本要求】 3dMax 2008及更高版本 【安装方法】 TubeChart插件无需安装,使用时直接拖动插件脚本文件到3dMax视口中打开即可࿰…...
基于SSM土家风景文化管理系统的设计
管理员账户功能包括:系统首页,个人中心,用户管理,景点分类管理,热门景点管理,门票订单管理,旅游线路管理,系统管理 前提账号功能包括:系统首页,个人中心&…...

C++超强图片预览器
下载 文件打开关联 关键代码 uint32_t getSrcPx3(const cv::Mat& srcImg, int srcX, int srcY, int mainX, int mainY) const {cv::Vec3b srcPx = srcImg.at<cv::Vec3b>(srcY, srcX);intUnion ret = 255;if (curPar.zoomCur < curPar.ZOOM_BASE && src…...

网络搜索引擎Shodan(2)
声明:学习视频来自b站up主 泷羽sec,如涉及侵权马上删除文章 声明:本文主要用作技术分享,所有内容仅供参考。任何使用或依赖于本文信息所造成的法律后果均与本人无关。请读者自行判断风险,并遵循相关法律法规。 感谢泷…...

【Tableau】
Tableau 是一款强大且广泛使用的数据可视化和商业智能(BI)工具,用于帮助用户分析、探索和呈现数据。它通过直观的拖放界面,允许用户轻松创建动态仪表板和报告,而无需编写代码。Tableau 可处理多种数据源,如…...

分类与有序回归
分类问题 分类问题,例如分类猫、狗、猪时,使用数字进行表示为1,2,3。而1、2、3之间有大小,分类算法为了平衡标签之间的差异,使得损失公平,会使用one-hot编码。例如,分别使用&#x…...

Mac如何实现高效且干净的卸载应用程序
使用Mac卸载应用程序,你还在使用废纸篓这个办法吗,看不见卸载了什么,看不见清理了多少,真的不会有残留吗 XApp Mac上的卸载专家,强大的垃圾逻辑检测,垃圾扫描更全面,卸载更干净 使用简单&#…...
LaTex中的常用空格命令
【LaTex中的常用空格命令】 在 LaTeX 中,有几个常用的空格指令: ● \,:一个小空格,通常用于在数学公式中插入较小的间距。● \quad:一个等宽空格,相当于当前字体尺寸下的字符宽度。 ● \qquad:两…...

k8s 1.28.2 集群部署 Thanos 对接 MinIO 实现 Prometheus 数据长期存储
文章目录 [toc]什么是 ThanosThanos 的主要功能Thanos 的架构组件Thanos 部署架构SidecarReceive架构选择 开始部署部署架构创建 namespacenode-exporter 部署kube-state-metrics 部署Prometheus Thanos-Sidecar 部署固定节点创建 label生成 secretMinIO 配置etcd 证书 启动 P…...

域渗透AD渗透攻击利用 python脚本攻击之IPC连接 以及 python生成exe可执行程序讲解方式方法
Python脚本批量检测ipc连接 import os, timeips [192.168.1.121,192.168.1.8 ] users {administrator,hack,hack1,test, } passs {123qq.com,456qq.com,Admin12345 } for ip in ips:for user in users:for mima in passs:exec1 "net use \\" "\\" i…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
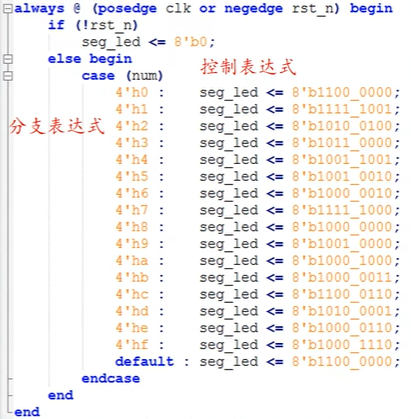
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

十二、【ESP32全栈开发指南: IDF开发环境下cJSON使用】
一、JSON简介 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,具有以下核心特性: 完全独立于编程语言的文本格式易于人阅读和编写易于机器解析和生成基于ECMAScript标准子集 1.1 JSON语法规则 {"name"…...
