数据结构与算法分析:你真的理解图算法吗——深度优先搜索(代码详解+万字长文)
一、前言
图是计算机科学中用来表示复杂结构信息的一种基本结构。本章我们会讨论一些通用的围表示法,以及一些频繁使用的图算法。本质上来说,一个图包含一个元素集合(也就是顶点),以及元素两两之间的关系(也就是边),由于应用范围所限,本章我们仅仅讨论简单图,简单围并不会如(a)那样有一个顶点的一条边是自己指向自己,以及不会如(b)那样一对顶点之间存在多条边。
一个图G=(V.E)由一个顶点集V以及一个边集E组成,算法中通常会出现如下几种图:
无向图
顶点(u,v)之间的关系模型不需要考虑关系的方向如何。在处理对称信息时,这种图非常有用。例如,汽车可以在A镇和B镇之间的路上双向行驶。
有向图
顶点(u,v)之间的关系和顶点(vu)之间的关系不同,后者或许不存在。例如,一个提供驾驶信息的程序必须存储单线道路的信息,以避免给出错误的方向。
有权图
顶点(u,v)之间的关系是有权重的,可以是数值的也可以是非数值的。例如,在A镇和B镇之间的道路有公里数,当然也包含了等袋时间这个信息。
超图
在顶点(w,v)之间可能存在多种关系,本章我们将讨论限定在简单图上。
如果图中任意两点之间都存在一条边,那么这个围是连通图。一个有向有权图的定义为:一个非空顶点集合( V n V_n Vn… V n − 1 V_{n-1} Vn−1)一个有向的边集合,每对顶点之间只有一条边,以及每条边上都有一个正权值。在很多应用中,这个权值被认为是距离或者开销。对某些应用来说,我们希望能够放宽权值必须为正的限制(例如,负值可以反映利润情
况),但是我们必须高度关注这样做的后果。考虑下图的有向有权图,它由6个顶点4条边组成。存储这个图有两个标准的数据结构:它们都显式地存储了权值,隐式表示了边的方向。

一种数据结构叫邻接表,如下图所示:

下图则是表明了如何用一个内阶的邻接知阵来存健有向有权图,每个维度可以被索引。条目A[i][j]存储的是从 V i V_{i} Vi到 V j V_{j} Vj的边的权值,当A[i][j]=0时,顶点,和頂点v,之间不存在边。使用邻接知阵表示法,在加一条边只要要常数时间。

我们他可以使用邻接表和邻接矩阵来存储无向图。看看下图6-5的无向图,我们使用< v 0 , v_{0}, v0, v 1 , v_{1}, v1,…… v k − 1 v_{k-1} vk−1>来描述一条有k个顶点的路,这条路遍历了k<1条边,一个有向图的路径是由同一方向的边组成。在下图中,路径< v 0 , v_{0}, v0, v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4,>是有效的。环是一个多次包含了同一个顶点的路径。一个环通常用其最小形式表示,在下图中,在路径< v 0 , v_{0}, v0, v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4, v 2 , v_{2}, v2, v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4, v 2 , v_{2}, v2,>中存在一个环,这个环可以用 v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4, v 2 , v_{2}, v2, v 1 v_{1} v1来表示。注意上上上个图的有向有权图权图,存在一个环< v 3 , v_{3}, v3, v 3 , v_{3}, v3, v 3 , v_{3}, v3,>.

存储问题
当使用部接表来存储无向图时,同一条边(w,v)在邻接表中出现了两次,一次是在的邻接节点健表,一次是在v的邻接节点键表。因此,相比同样数目的顶点和边的有向图,无向图在邻接表中存储所需要的存储空间是前者的两倍,当使用邻核知阵来存储无向图时,你必须保证条目A[AU)=AU114,不需要任何的额外存储空间。
当使用二维矩阵来表示元素集合中内个元素的潜在关系时,需要注意一些事项。首先,矩阵需要 n 2 n^2 n2个元素的存储空间,即使有时候元素之间的关系集合非常小。在这些情况下,也就是所谓的稀疏围,由于计算机内存的限制,不可能存储超过数千个顶点的图。例如,Java虚拟机使用默认值256MB,创建一个二维的int[4096][4096]矩阵就已经超出可用内存。即使程序员能够在一台有着更多内存的计算机上执行程序,事实上创建的矩阵规模存在一个固定的上界,另外,在大规模矩阵中存储稀疏键图,遍历矩阵来寻找边的操作的开销会很大,并且这种存储方法也限制了更多的改进。第二,当顶点之间有多种关系时,不适合使用矩阵,为了能够在矩阵中存储这种关系,矩阵中每一个元素将会当作一个表。
每一种邻接表示法都存储了相同的信息,假设,你写了一个程序,需要计算出世界上任意两个城市之间的最便宜的航班。每条边的权重和两个城市之间最便宜直航的价格有关(假设载线不会中转),根据2005年国际机场协会(ACI)发布的一份接告,世界上有总共1659个机场,这样也就需要一个有2752281个条目的二维矩阵。那么就有一个问题:“多少条目是有值的”,它的答案率决于直航航线的数目,ACI的接告也显示,2005年有71600000次 “航空括动”, 简单地说每天有大概196164次航班。即使所有的航班都是在两个不同机场之间的直航(虽然直航的数目要比这个小很多),这个矩阵也有93%是空值 ——一个非常好的稀疏矩阵的例子!当使用一个邻接表表示无向图时,我们可以使用一些方法来减少需要的存储空间,假设一个顶点的部接顶点为:2.8.1.5.3.10.11和4,首先,这些部接顶点会以升序来存储,这样做能修快速地定位是否存在一条边(w.y),在这种结构下,虽然有8个邻接顶点,但是确定是否边(u,6)是否存在只需要6次比较。当然,添加一条边就不再是常数时间,这里我们需要权衡一下利弊。其次,为了能够更加高效的检查是否边(u,v)存在,邻接表可以存储邻接顶点的范围,例子中的邻接表中八个顶点可以减少到三个;1-5、8、10-11。这种方法也能够减少是否存在一条边的计算次数,不过这会降低添加或者删除边的效率。
图分析
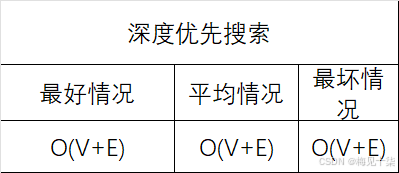
当使用本章的算法时,决定使用邻接表还是邻接矩阵的最重要因素是围是否为稀疏图。算法的性能是和围的顶点教IVIRRERRERR相关书一样,我们简化了性能的公式,无论在最好、最坏还是平均情况下,我们都使用V,E的大0记法来表示性能。
O(V)表示需要和图中的顶点数成直接比例的计算步数,但是图中边的密度他必须考虑,在稀疏图中,O(E)近似等于O(V),然而在稠密图中,它近似等于O( V 2 V^2 V2)。
我们将会看到,根据图的结构,一些算法会有两个变种,并且这两个变种的性能不尽相同,一个变种也许执行时间为O((V+E)*logV),而另外一个是O( V 2 + E V^2+E V2+E)。哪个更加高效呢?下表告诉我们这个答案取决于图G是稀疏图还是橋稠密图。对于稀疏图来说, O ( ( V + E ) ∗ l o g V ) \mathrm{O}((V{+}E)^{*}\mathrm{log}V) O((V+E)∗logV)虽然更加高效一点,而对于稠密图, O ( V 2 + E ) O(V^2+E) O(V2+E)就更加快速了,标记为“均衡图”的条目,这种图的期望性能在稀疏图和稠密图上都是相同的,为 O ( V 2 ) O(V^2) O(V2),在这些图上,边的数目大致等于 O ( V 2 / l o g V ) O(V^2/log V) O(V2/logV)。

问题
使用图结构可以解决很多问题。本章我们只是讨论其中一些,不过你仍然有机会寻找到一些我们没有讨论的问题,然后去研究,给定一个用边来定义的图,很多问题会和图中两顶点之间的最短路径相关,路的长度就是路上边的长度之和。在“单源最短路径”这个问题上,给定一个顶点,我们需要计算出到图中其他所有顶点的最短路径。在“对顶点间最短路径”问题中,我们需要计算图中所有的顶点对(w.v)之间的最短路径。有些问题则是在更加深人地使用了图的结构,我们可以从一个图中构造出一个最小生成树(MST)。最小生成树是一个无向有权图,是原图边的一个子集,但是,原图的顶点仍然是连通的,而边的权值总和最小,在“最小生成树算法”一节,我们将会描述如何高效地解决这个问题。
我们首先从如何探索图开始讨论。两个最常使用的搜索方法是深度优先搜索(DFS)和广度优先搜索(BFS)。
二、算法描述
考虑下图左边的迷宫,在经过一尝试后,一个孩子能够快速地找到从起点s到终点t的路,但是计算机解决这个问题看起来就比较复杂,一种方法是假设离目标并不太远,然后做尽可能多的深度移动,也就是说,只要可以,随机选择一个方向,然后向这个方向前进,标记一下起点,如果你走上一条死路,或者不能在不重新访问顶点的情况下做任何深度移动,那么就会遇到另一条未访问的分支上,并且向这个方向前进。下图右边的数字表示的是一个解的分支点。事实上,在这个解中,我们访问了迷中的所有点。

我们能够用一个包含了点和边的图来表示上图的迷宫。一个顶点表示迷宫中的每一个分支点(在上图的右边用数字标记) ,当然也包括“末路点”。如果迷宫中在两个顶点之间存在一条有向路,并且在这个方向上没有其他的选择,那么我们就说存在一条边。从上图得到的迷宫的无向图表示如下图所示,每一个顶点都有一个唯一标识符。

为了解决这个问题,我们需要知道在图 G=(V,E)的顶点s到顶点r是否存在一条路。本例中,所有的边都是无向的,但是即使在迷宫上加一些限制条件,我们也能够非常容易地将其看成有向图。下图的详解包括了用伪代码描述的深度优先搜索。深度优先搜索的核心是递归的 dfs_visit(u)操作,这个操作访问之前没有访问过的顶点u。并且这个操作通过对顶点染色记录下了搜索进程。顶点可能会染成如下三种颜色;
白色
顶点还未访问。
灰色
顶点已经被访向过了,但是其可能还有没有被访问过的顶点。
黑色
顶点以及其所有的邻接顶点都已经被访向过了。
首先,所有的顶点初始为白色,然后深度优先搜索在源顶点 s 上调用 dfs_visit,在对 u 所有的未访向邻接顶点(它们为白色)递归调用 dfs_visit 之前,dfs_visit(u)将 u 染成灰色。一旦这些递归调用完成,那么我们将 u 染成黑色,然后函数返回。当递归函数 dfs_visit 返回,深度优先搜索开始回溯,直到回溯到一个有邻接顶点未被访问过的顶点(事实上,回溯到标记为灰色的顶点)。
对有向和无向图来说,深度优先搜索从 s 开始,访问了图中所有 s 可达的顶点。如果 G 中仍然有未访问,但是从s不可达的顶点存在,深度优先搜索将会随机从其中选择一个作为源点,然后重复操作。这个过程将会一直重复,直到 G 中所有的顶点都被访问。
在这个执行过程中,深度优先搜索遍历图中的边,计算和复杂的图结构有关的信息。深度优先搜索维护一个计数器,在一个顶点第一次被访问(标记为灰色)和完成在这个顶点上的深度优先搜索(标记为黑色)时,这个计数器增加计数。对于每个顶点,深度优先搜索记录如下信息。
pred[v]
前驱顶点,用来恢复从源点 s 到顶点 v 的路。
discovered[v]
其值为当深度优先搜索第一次访向 v 时,计数器增加后的值,简写为 d[v]。
finished[v]
其值为完成在这个顶点 v 上的深度优先搜索,计数器增加后的值,简写为 f[v]。
顶点访问的顺序将会改变计数器的值。所以需要注意邻接节点的顺序。对很多构建在深度优先搜索上的算法,深度优先搜索计算出来的信息都是非常有用的,包括拓扑排序,寻找强连通部,寻找网络中潜在的弱点。让我们来看看上图,假设顶点的邻接顶点是升序排列。那么计算出来的信息如下图所示。当计数器为 18,顶点 8 正在被访问时,让我们看看图中顶点的颜色。图中有些部分(例如标记为黑色的点)已经被完全搜索井且不会被重复访问。我们需要注意白色顶点的 d 都将大于 18(因为它们现在还没有被访间),以及黑色顶点的f都小于等于 18,因为它们已经被完全搜索过,灰色顶点的 d 小于等于 18,f 大于 18,因为它们现在正处于某条递归访问的路上。

深度优先搜索没有对图的一个整体认识,所以它是盲目地搜索顶点<5,6,7,8>,即使是南辕北辙。一旦深度优先搜索结束,pred[]的值能够用来生成一条从任意顶点到源点 s 的路。当然,这条路也许不会是最短路径,例如<s,1,3,4,5,9,>,但是最短的路径是<s, 6, 5,9, > (这里的最短路径指的是s到r经过的点的个数最少) 。
深度优先搜索计算三个数组。d[v]表示的是 v 第一次被访问时,计数器的值。pred[v]是深度优先搜索时,顶点 v 的先驱顶点。[fv]则是当 v 被完全访问过之后,计数器的值,即 dfs_visit(v)之后计数器的值。如果原图是不连通的,那么根据 pred[]的值实际上可以得到一个由深度优先树组成的深度优先森林。对于森林中的树来说,它们根节点的 pred[r]的值都为-1。此算法对于有向图和无向图同样适用。
深度优先搜索(DFS)的基本过程:
深度优先搜索(DFS)
算法步骤:
-
初始化:
- 创建一个栈(可以使用递归实现)来存储待访问的节点。
- 创建一个布尔数组
visited,用于标记每个节点是否已访问。
-
遍历:
- 从起始节点开始,将其推入栈并标记为已访问。
- 当栈不为空时,执行以下操作:
- 从栈中弹出一个节点
u。 - 访问节点
u,进行必要的处理(如打印或存储)。 - 遍历
u的所有邻接节点v:- 如果节点
v未被访问,则将其推入栈并标记为已访问。
- 如果节点
- 从栈中弹出一个节点
三、复杂度分析
深度优先搜索只需要在遍历图时存储每个顶点的频色(白、灰或者黑)。因此深度优先搜索在逾历围时,只需要很小的存储开销。深度优先搜索能够在数组中存储其遍历图时的信息。事实上,深度优先搜索对图的唯一要求是能够遍历给定顶点的所有邻接顶点,于是这样,我们能够在复杂的数据结构上方便地进行深度优先搜索。因为 df_visit 函数将原图看做一个只读结构。但是,深度优先搜索仅仅依靠当前的信息,是一种盲目的搜索,它并没有一个明智的计划来快速达到目标顶点 t。
图中的每一个顶点都会调用递归的dfs_visit函数一次。dfs_search中的循环不会执行超过n次。在dfs_visit函数中,每一个邻接顶点都要被检查,对于有向围来说,每一条边都只会遍历一次,然而在无向图中,它们会被遍历一次然后会被检查一次,在任何情况下,性能开销都是O(V+E)。
四、适用情况
以下是一些常见的适用场景:
图的遍历:
DFS 可以用于遍历图中的所有节点,适合于寻找所有连通分量。
路径查找:
在寻找从一个节点到另一个节点的路径时,DFS 可以有效地探索所有可能的路径,特别是在解决迷宫问题时。
拓扑排序:
在有向无环图(DAG)中,DFS 可以用于拓扑排序,帮助确定任务的优先级或依赖关系。
解决约束满足问题:
如数独、八皇后问题等,DFS 可以通过递归尝试所有可能的放置方式,寻找有效解。
生成组合和排列:
在生成集合的所有组合或排列时,DFS 是一个有效的选择。
强连通分量:
在有向图中,DFS 可以用于查找强连通分量,通过 Tarjan 或 Kosaraju 算法实现。
解决游戏问题:
在一些回合制游戏中(如棋类游戏),DFS 可以用于评估所有可能的游戏状态,帮助选择最佳策略。
图的颜色问题:
在一些图的颜色问题中,DFS 可以用于验证图是否可着色或寻找可行的着色方案。
寻找特定节点:
当需要寻找特定特征的节点时,DFS 可以在较深的层次上更早找到目标。
注意事项:
空间复杂度:DFS 在深度较大的图中可能会导致栈溢出,因此在处理非常深的树或图时,要考虑使用迭代的方式或增加栈的大小。
性能:在某些情况下(如图较大且稀疏时),DFS 可能不是最优选择,这时广度优先搜索(BFS)或其他算法可能更合适。
五、算法实现
下面是深度优先搜索的C++实现:
#include <iostream>
#include <vector>
#include <list>using namespace std;// 定义边的类型枚举
enum edgeType { Tree, Backward, Forward, Cross };// 定义顶点颜色枚举
enum class vertexColor { white, gray, black };// 定义边标签结构
struct EdgeLabel {int u, v;edgeType type;EdgeLabel(int _u, int _v, edgeType _type) : u(_u), v(_v), type(_type) {}
};// 定义图的类型(使用邻接表表示)
class Graph {
public:vector<vector<int>> adj;Graph(int n) : adj(n) {}void addEdge(int u, int v) {adj[u].push_back(v);}const vector<int>& operator[](int u) const {return adj[u];}auto begin(int u) const {return adj[u].begin();}auto end(int u) const {return adj[u].end();}
};void dfs_visit(Graph const& graph, int u, vector<int>& d, vector<int>& f, vector<int>& pred, vector<vertexColor>& color, int& ctr, list<EdgeLabel>& labels);// 访问顶点 u 并更新信息
void dfs_visit(Graph const& graph, int u, vector<int>& d, vector<int>& f, vector<int>& pred, vector<vertexColor>& color, int& ctr, list<EdgeLabel>& labels)
{color[u] = vertexColor::gray; // 将顶点 u 标记为灰色(正在访问)d[u] = ++ctr; // 记录发现时间for (int v : graph[u]) {if (color[v] == vertexColor::white) { // 如果顶点 v 仍然是白色(未访问)pred[v] = u; // 更新前驱dfs_visit(graph, v, d, f, pred, color, ctr, labels); // 递归访问 v}}color[u] = vertexColor::black; // 将顶点 u 标记为黑色(完成访问)f[u] = ++ctr; // 记录完成时间// 处理所有邻接顶点for (auto ci = graph.begin(u); ci != graph.end(u); ++ci) {int v = *ci;edgeType type = Cross; // 初始化边的类型为交叉边if (color[v] == vertexColor::white) {type = Tree; // 如果 v 是白色,则为树边}else if (color[v] == vertexColor::gray) {type = Backward; // 如果 v 是灰色,则为回边}else {if (d[u] < d[v]) {type = Forward; // 如果 d[u] < d[v],则为前向边}}labels.push_back(EdgeLabel(u, v, type)); // 添加边标签}
}// 从顶点 s 开始执行深度优先搜索
void dfs_search(Graph const& graph, int n, vector<int>& d, vector<int>& f, vector<int>& pred, vector<vertexColor>& color, list<EdgeLabel>& labels) {int ctr = 0; // 发现和完成时间的计数器for (int u = 0; u < n; u++) {if (color[u] == vertexColor::white) { // 如果顶点 u 是白色dfs_visit(graph, u, d, f, pred, color, ctr, labels); // 开始访问}}
}int main() {// 创建一个包含 5 个顶点的图Graph graph(5);graph.addEdge(0, 1);graph.addEdge(0, 2);graph.addEdge(1, 3);graph.addEdge(1, 4);graph.addEdge(2, 4);int n = 5; // 顶点数量vector<int> d(n, 0); // 发现时间vector<int> f(n, 0); // 完成时间vector<int> pred(n, -1); // 前驱vector<vertexColor> color(n, vertexColor::white); // 顶点颜色list<EdgeLabel> labels; // 边标签// 从顶点 0 开始深度优先搜索dfs_search(graph, n, d, f, pred, color, labels);// 输出发现和完成时间cout << "顶点\t发现时间\t完成时间\n";for (int i = 0; i < n; i++) {cout << i << "\t" << d[i] << "\t\t" << f[i] << "\n";}// 输出边标签cout << "\n边标签:\n";for (const auto& label : labels) {cout << "(" << label.u << ", " << label.v << ") : " << static_cast<int>(label.type) << "\n";}return 0;
}
下面是两个不同写法的dfs_visit函数的对比:
void dfs_visit(int u, int& time, vector<int>& d, vector<int>& f, vector<int>& color, vector<vector<int>>& G) {color[u] = 1;d[u] = ++time;for (int v : G[u]) {if (color[v] == 0) {dfs_visit(v, time, d, f, color, G);}}color[u] = 2;f[u] = ++time;
}
/*
这两个 dfs_visit 函数在功能上都是执行深度优先搜索(DFS),但实现上有一些明显的差异。以下是对比和说明:1. 参数类型和数量
上段代码中的 dfs_visit:接受的参数有多个,包括图的结构、前驱节点数组、颜色数组、时间计数器、边标签列表等。
使用的颜色类型是枚举 vertexColor,用来表示未访问、正在访问和已完成。
新代码中的 dfs_visit:参数较少,主要是顶点 u、时间 time、发现时间数组 d、完成时间数组 f、颜色数组 color 和图 G。
颜色使用整数(0, 1, 2)来表示状态,分别对应未访问、正在访问和已完成。
2. 颜色管理
上段代码:
使用 vertexColor 枚举来表示顶点的状态,赋值 gray 表示正在访问,赋值 black 表示已完成。
新代码:
使用简单的整数来表示状态,color[u] = 1 代表正在访问,color[u] = 2 代表已完成。
3. 边标签处理
上段代码:在遍历邻接点时,记录边的类型(树边、回边、前向边、交叉边),并将这些信息存储在边标签列表中。
新代码:没有处理边标签,专注于顶点的发现和完成时间。
4. 递归调用
上段代码:在递归调用 dfs_visit 之前更新前驱节点数组 pred。
新代码:没有更新前驱节点的信息,这可能影响对DFS树的重建或后续操作。
5. 代码风格
上段代码:
使用更丰富的结构体和类型定义,增加了代码的可读性和维护性。
新代码:
相对简单直接,适合快速实现DFS,但可能在后续分析中缺少某些信息。
总结
这两个函数的主要目的是相同的,都是实现深度优先搜索。上段代码提供了更多的功能和信息处理(如前驱记录和边标签),而新代码则相对简单,适用于基本的DFS实现。如果你的目标是构建DFS树或分析图的结构,上段代码可能更适合;如果只需要基本的DFS遍历,新代码足够用。
*/
如果d[]和f[]不需要,那么这些值的计算过程(以及将其作为函数参数)可以从上例中的代码删除掉。深度优先搜索可以得到关于图中边的额外信息。尤其在深度优先森林中,有四种边。
树边
对于所有pred[v]-u的顶点v,dfs_visit(u)坊问边(w.v)来遍历图。这些边记录了深度优先搜索的进程。上图中的边(s,1)就是一个很好的例子。
后边
当dfs_visit(u)处理到顶点时,如果v是的邻接顶点并且是灰色,那么深度优先搜索就会知道它已经访问过这个顶点。图6-10中的边(8.3)就是一个很好的例子。
前边
当dfs_visit(u)处理到顶点的,如果v是的部接顶点,v的颜色是黑色,而且&在v之前被访问,那么边(w,v)是一个前边。那么深度优先搜索就会知道它已经访问过这个顶点了。图6-10中的边(5,9)就是一个很好的例子。
交叉边
当dfs_visit(u)处理到顶点时,如果的邻接顶色是黑色,而且色是黑色,而且在v之后被访问,那么边(u,v)是一个交叉边。交叉边只是在有向图中存在。标记这些边的代码在上例中。对于无向图,边(w.v)可能会被标记很多次,但是一般来说,只有在这条边第一次被标记时其标记有效。
六、算法优化
以下是一些常见的优化策略:
剪枝:
在搜索过程中,如果发现某个路径不可能满足目标条件,可以提前结束该路径的搜索,从而减少不必要的计算。
使用迭代加深:
结合深度优先搜索和广度优先搜索的优点,通过在一定深度限制内进行多次深度优先搜索,可以在不消耗太多内存的情况下找到最优解。
路径存储:
对已访问的节点进行标记,避免重复访问,从而减少时间复杂度。使用集合或哈希表来存储已访问节点,可以快速检查节点是否已经被访问。
深度限制:
对于某些问题,可以设置最大深度限制,防止在深度过大的情况下出现栈溢出,尤其是在递归实现中。
调整搜索顺序:
根据启发式信息调整子节点的访问顺序,可以更快地找到目标节点。例如,优先搜索可能更有希望的路径。
记忆化搜索:
将中间结果缓存起来,避免重复计算同样的子问题,提高效率。
图的表示:
选择合适的数据结构表示图(如邻接表或邻接矩阵)可以提高DFS的性能,尤其是在稀疏或密集图中。
七、引用及参考文献
1.《算法设计手册》
相关文章:

数据结构与算法分析:你真的理解图算法吗——深度优先搜索(代码详解+万字长文)
一、前言 图是计算机科学中用来表示复杂结构信息的一种基本结构。本章我们会讨论一些通用的围表示法,以及一些频繁使用的图算法。本质上来说,一个图包含一个元素集合(也就是顶点),以及元素两两之间的关系(也就是边),由于应用范围所限,本章我们仅仅讨论简单图,简单围并不会如(a…...
LinkedList 分析
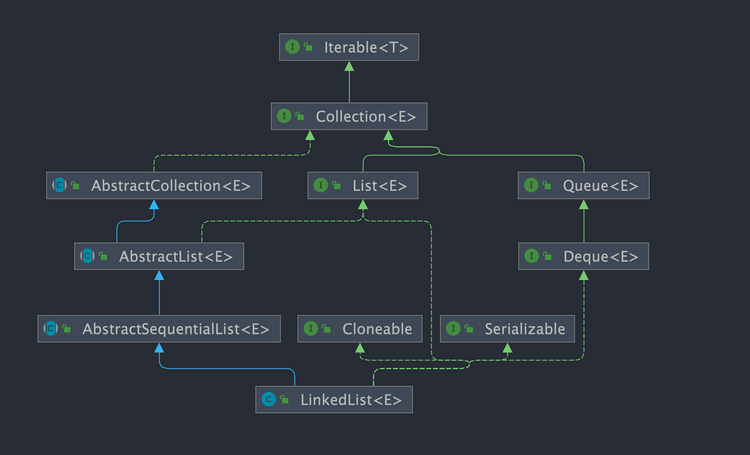
LinkedList 简介 LinkedList 是一个基于双向链表实现的集合类,经常被拿来和 ArrayList 做比较。关于 LinkedList 和ArrayList的详细对比,我们 Java 集合常见面试题总结(上)有详细介绍到。 双向链表 不过,我们在项目中一般是不会使用到 Link…...
【C/C++】模拟实现strlen
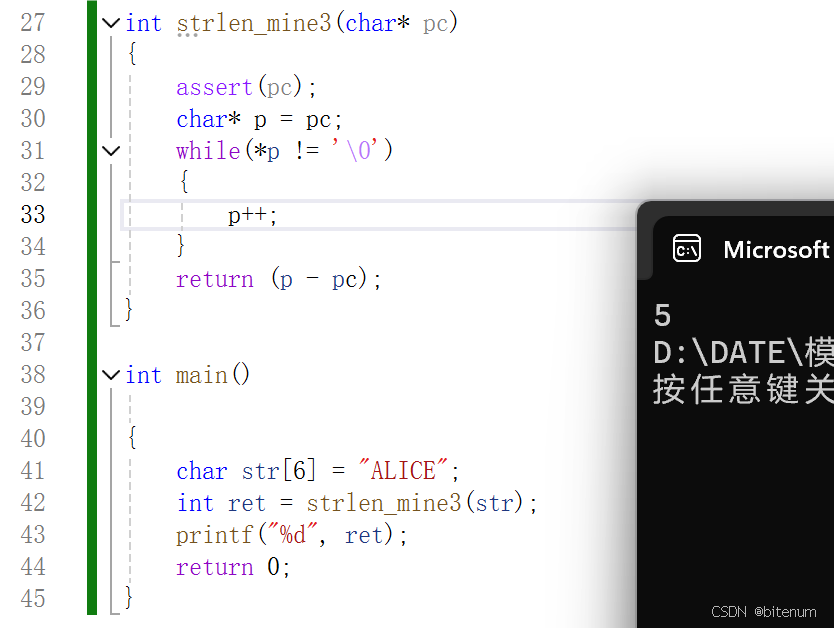
学习目标: 使用代码模拟实现strlen。 逻辑: strlen 需要输入一个字符串数组类型的变量,并且返回一个整型类型的数据。strlen 需要计算字符串数组有多少个元素。 代码1:使用计数器 #define _CRT_SECURE_NO_WARNINGS 1 #include&…...
mybatis从浅入深一步步演变分析
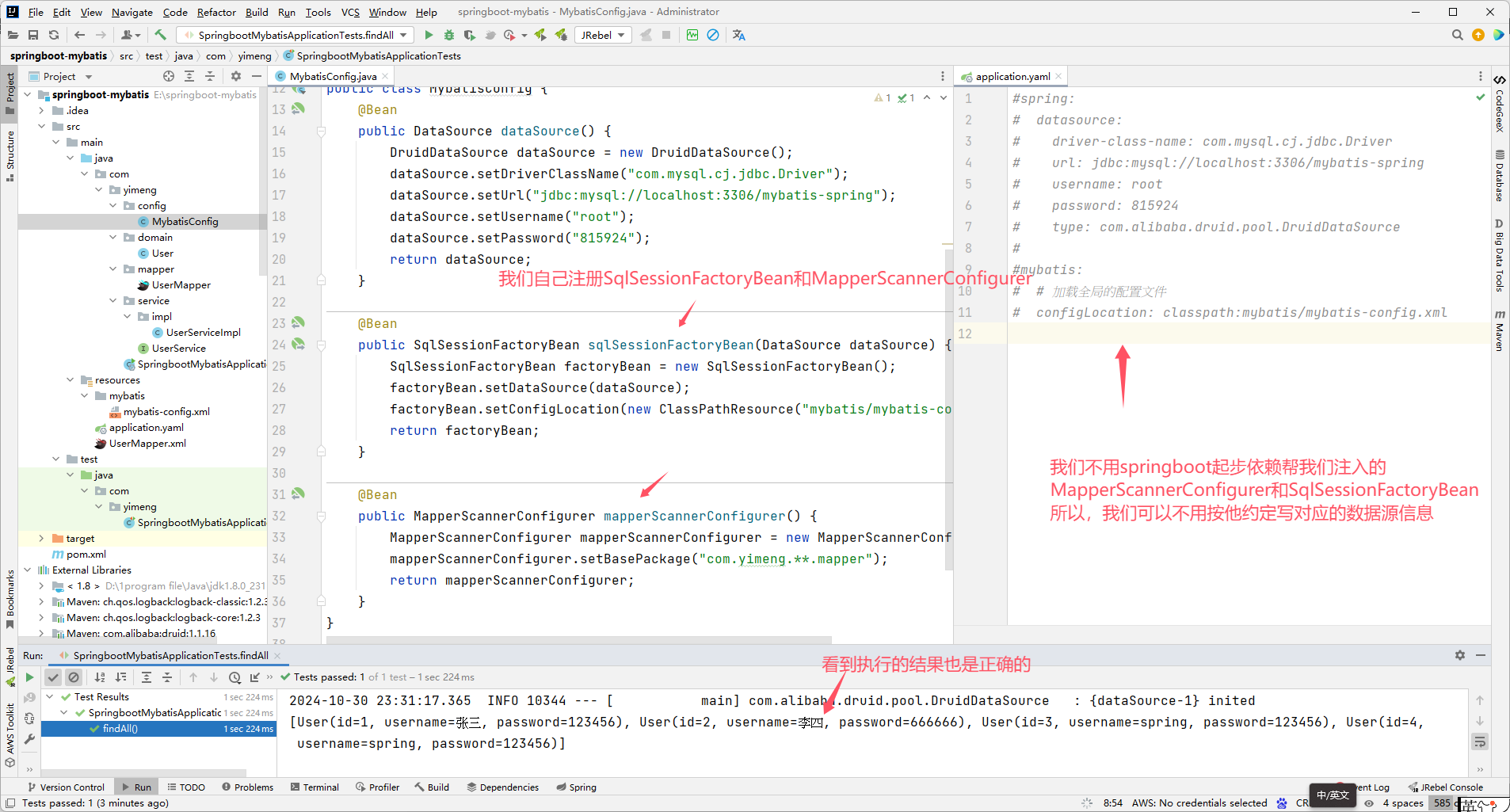
mybatis从浅入深一步步演变分析 版本一:不使用代理(非spring) package com.yimeng.domain;public class User {private int id;private String username;private String password;public int getId() {return id;}public void setId(int id…...
Java阶段三02
第3章-第2节 一、知识点 面向接口编程、什么是spring、什么是IOC、IOC的使用、依赖注入 二、目标 了解什么是spring 理解IOC的思想和使用 了解IOC的bean的生命周期 理解什么是依赖注入 三、内容分析 重点 了解什么是spring 理解IOC的思想 掌握IOC的使用 难点 理解IO…...
【Linux】掌握库的艺术:我的动静态库封装之旅
🌈个人主页:Yui_ 🌈Linux专栏:Linux 🌈C语言笔记专栏:C语言笔记 🌈数据结构专栏:数据结构 🌈C专栏:C 文章目录 1.什么是库1.2 认识动静态库1.2.1 动态库1.2.2…...
UE5动画控制 基础
素材 mixamo先去选择一个character 点击下载 就这个下载下来 然后选几个animation, 记得勾选 把动作下载了 without skin就是只要动作 然后把他们放在一个文件夹里先 UE里导入 找一个文件夹,直接拖拽进来那个character的fbx,默认配置就…...

流畅!HTMLCSS打造网格方块加载动画
效果演示 这个动画的效果是五个方块在网格中上下移动,模拟了一个连续的加载过程。每个方块的动画都是独立的,但是它们的时间间隔和路径被设计为相互协调,以创建出流畅的动画效果。 HTML <div class"loadingspinner"><…...

linux命令之top(Linux Command Top)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 本人主要分享计算机核心技…...
笔记)
数据结构-希尔排序(ShellSort)笔记
看动画理解 【数据结构】八大排序(超详解附动图源码)_数据结构排序-CSDN博客 一 基本思想 先选定一个整数gap,把待排序文件中所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的元素进行排序。 然后将gap逐渐减小重复上…...

Junit + Mockito保姆级集成测试实践
一、做好单测,慢即是快 对于单元测试的看法,业界同仁理解多有不同,尤其是在业务变化快速的互联网行业,通常的问题主要有,必须要做吗?做到多少合适?现在没做不也挺好的吗?甚至一些大…...

软件项目管理要点
一.项目管理 1.盈亏平衡分析 销售额固定成本可变成本税费利润 当利润为0的时候就是盈亏平衡点。 2.范围管理 范围定义的输入包括:项目章程、项目范围管理计划、组织过程资产、批准的变更申请。 3.时间管理 项目时间管理中的过程包括活动定义、活动排序、活动的资…...

ESP8266 连接 MQTT 服务器EMQX 连接MQTTX
目录 1.先用有一台自己的云服务器 2. 使用FinalShell连接阿里云云服务器ECS 3.安装宝塔 4.在云服务器打开8888端口 5.使用外网面板地址打开宝塔面板 6.安装Docker 7.下载emqx 8.打开emqxWeb 界面 9.下载MQTTX 10.EMQX加一个客户端 11.开始通信 12.加入单片机ESP8266 …...

Python中如何处理异常情况?
1、Python中如何处理异常情况? 在Python中,处理异常情况通常使用try/except语句。try语句块包含可能会引发异常的代码,而except语句块包含处理异常的代码。如果try块中的代码引发了异常,控制流将立即转到相应的except块。 以下是…...

openpnp - 在openpnp中单独测试相机
文章目录 openpnp - 在openpnp中单独测试相机概述笔记END openpnp - 在openpnp中单独测试相机 概述 底部相机的位置不合适, 重新做了零件,准备先确定一下相机和吸嘴的距离是多少才合适。 如果在设备上直接实验,那么拆装调整相机挺麻烦的。 准备直接在电…...

Spark窗口函数
1、 Spark中的窗口函数 窗口就是单纯在行后面加一个列 可以套多个窗口函数,但彼此之间不能相互引用,是独立的 窗口函数会产生shuffle over就是用来划分窗口的 (1) 分组聚合里面的函数,基…...

Idea、VS Code 如何安装Fitten Code插件使用
博主主页:【南鸢1.0】 本文专栏:JAVA 目录 编辑 简介 所用工具 1、Idea如何安装插件 1.idea下载插件 2.需要从外部下载然后在安装, 2、VS Code如何安装插件 总结 简介 Fitten Code是由非十大模型驱动的AI编程助手,它可以自动生成代…...

elasticsearch7.x在k8s中的部署
一、说明 二、思路 三、部署 1、建nfs服务器 2、建持久卷 3、部署elasticsearch 四、附件 ?pv.yaml内容 elasticsearch.yaml内容 一、说明 本文章内容主要的参考来源是https://www.cnblogs.com/javashop-docs/p/12410845.html,但参考文献中的elasticsearc…...

校园社团信息管理平台:Spring Boot技术实战指南
3系统分析 3.1可行性分析 通过对本校园社团信息管理系统实行的目的初步调查和分析,提出可行性方案并对其一一进行论证。我们在这里主要从技术可行性、经济可行性、操作可行性等方面进行分析。 3.1.1技术可行性 本校园社团信息管理系统采用SSM框架,JAVA作…...

【Linux】从内核角度理解 TCP 的 全连接队列(以及什么是 TCP 抓包)
文章目录 概念引入理解全连接队列内核方面理解Tcp抓包方法注意事项 概念引入 我们知道,TCP的三次握手是由TCP协议 自动处理的,建立连接的过程与用户是否进行accept无关,accept()的作用主要是为当前连接创建一个套接字,用于进行后…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
