【考研数学 - 数二题型】考研数学必吃榜(数二)
数学二
suhan, 2024.10
文章目录
- 数学二
- 一、函数
- ❗1.极限
- 1.1求常见极限
- 1.2求数列极限
- 1.2.1 n项和数列极限
- 1.2.2 n项连乘数列极限
- 1.2.3 递推关系定义的数列极限
- 1.3确定极限式中的参数
- 1.4无穷小量阶的比较
- 2.连续
- 2.1判断是否连续,不连续则判断间断点类型
- 2.2证明题
- 二、一元函数微分学
- 1.导数、微分的定义
- 1.1导数定义求极限
- 1.2导数定义求导数
- 1.3导数定义判定可导性
- 2.导数几何意义
- ❗3.求导
- 3.1复合函数
- 3.2隐函数
- 3.3参数方程
- 3.4反函数
- 3.5对数求导法
- 3.6高阶导数
- 4.导数应用
- 4.1单调性、极值、最值
- 4.1.1求极值
- 4.1.2求最值
- 4.2曲线凹凸性、拐点、渐近线、曲率
- 4.2.1渐近线
- 4.2.2曲率
- 4.3方程的==根==的存在性和个数
- 4.4证明:不等式
- 4.5证明:微分中值定理
- 4.5.1证明∃ξ∈(a,b),使得F[ξ, f(ξ), f'(ξ)]=0成立
- 4.5.2证明存在两个中值点η,ξ∈(a,b),使得F[ξ, f(ξ), f'(ξ), η, f(η), f'(η)]=0成立
- 4.5.3证明∃ξ∈(a,b),使得F[ξ, f^(n)^(ξ)]≥0成立
- 三、一元函数积分学
- 1.不定积分
- ❗2.定积分
- 2.1定积分概念、性质、几何意义
- 2.2定积分计算
- 2.3变限积分
- 2.4积分不等式
- 3.反常积分
- 3.1反常积分敛散性
- 3.2反常积分计算
- 4.定积分应用
- 4.1求面积 S
- 4.2求体积 V
- 4.3弧长 s
- 4.4旋转体的侧面积 S
- 4.5物理问题
- 四、常微分方程
- 1.微分方程
- 2.高阶方程降阶
- 3.高阶微分方程
- 4.综合题
- 4.1积分方程
- 4.2函数方程
- 五、多元函数微分学
- 1.重极限、连续
- 1.1求极限
- 1.2证明极限不存在
- 2.偏导数、全微分
- 2.1偏导数
- 2.1.1偏导数定义
- 2.1.2高阶偏导数
- 2.2.全微分
- 2.2.1全微分判断
- 2.2.1全微分计算
- 2.3复合函数
- 2.4隐函数
- 题型(求偏导数与全微分)
- 1)求一点处的偏导数与全微分
- 2)求已给出具体表达式函数的偏导数与全微分
- 3)含有抽象函数的复合函数的偏导数与全微分
- 4)隐函数的偏导数与全微分
- 4.极值、最值
- 4.1求无条件极值
- 4.2条件最值(拉格朗日乘数法)
- 六、二重积分
- 1.计算二重积分
- 2.累次积分:交换次序&计算
- 3.综合、证明
一、函数
❗1.极限
可用方法:
- 两个基本极限
- 洛必达法则
- 等价无穷小(x→0)
- 上下同除最大变量(无穷大)(x→∞)
- 泰勒公式
- 拉格朗日中值定理 p21
- 夹逼法则
- 定积分定义 p19
- 单调有界准则
【注意】从负方向趋近于1,那么实际上就是比1小;从正方向趋近于1,那么实际上就是比1大。
lim x → 1 + 1 x − 1 = + ∞ lim x → 1 − 1 x − 1 = − ∞ \lim_{x \rightarrow1^+} \frac1{x-1} = +\infty \\ \lim_{x \rightarrow1^-} \frac1{x-1} = -\infty \\ x→1+limx−11=+∞x→1−limx−11=−∞
e ∞ ≠ ∞ e^{\infty} ≠ \infty e∞=∞ 因为:
e + ∞ = + ∞ e − ∞ = 0 e^{+\infty} = +\infty \\ e^{-\infty} = 0 e+∞=+∞e−∞=0
同理:
arctan ( + ∞ ) = π 2 arctan ( − ∞ ) = − π 2 \arctan(+\infty) = \frac \pi 2 \\ \arctan(-\infty) = -\frac \pi 2 arctan(+∞)=2πarctan(−∞)=−2π
1.1求常见极限
- 首先,运用极限的运算法则(四则运算,连续函数的极限,复合函数的极限),确定极限是不是未定式极限。
- 两种基本的未定式极限是 0 0 \cfrac 00 00 型 和 ∞ ∞ \cfrac ∞∞ ∞∞ 型,这两种情形一般可以用洛必达法则来求。
- 其它未定式极限( 0 ⋅ ∞ , ∞ − ∞ , 1 ∞ , 0 0 , ∞ 0 0⋅∞,∞−∞,1^∞,0^0,∞^0 0⋅∞,∞−∞,1∞,00,∞0),要先化成上面的两种基本情形来求,然后用洛必达法则或者其它方法来求。
常用方法:
- 洛必达法则
- 等价无穷小
- 泰勒公式
【技巧】出现函数作为次方时候,可以提取一个同类型的到括号外面,构建出 ( a ψ − a ϕ ) = a ϕ ( a ψ − ϕ − 1 ) (a^{\psi}-a^\phi) = a^{\phi}(a^{\psi-\phi}-1) (aψ−aϕ)=aϕ(aψ−ϕ−1). 例如p20
1.2求数列极限
数列不连续,所有不可以直接使用洛必达法则,要先把不连续的数列变成连续的函数,使其可导。
【技巧】可以把最大无穷大的拿到括号外面来,让括号里面出现 1 ∞ \cfrac 1 ∞ ∞1 的形式。
1.2.1 n项和数列极限
-
夹逼法则
-
定积分定义 p19
前两者也会先用夹逼法则,再用定积分定义。
-
级数求和(数一三)
1.2.2 n项连乘数列极限
p33(《辅导讲义》)
1.2.3 递推关系定义的数列极限
p34
1.3确定极限式中的参数
可提出非零极限因子。分别先求a,再求b。
【技巧】当有 x → − ∞ x→-∞ x→−∞那么要提 − x -x −x;不想提 − x -x −x,就要令 x = − t x=-t x=−t,改变符号。
p38
1.4无穷小量阶的比较
比较两个无穷小等于 0 0 \cfrac 00 00 型的极限。所以常用方法:
- 洛必达法则
- 等价无穷小
- 泰勒公式
- 变化率
当然,最重要的是背的等价无穷小转换。
【技巧】只要有 x 在幂次方,例如:
( 1 + m ) x − 1 (1+m)^x-1 (1+m)x−1
那么就可以使用 e x − 1 ∼ x e^x - 1 \sim x ex−1∼x 和 ln ( 1 + x ) ∼ x \ln(1+x) \sim x ln(1+x)∼x:
e x ln ( 1 + m ) − 1 ∼ e x ⋅ m − 1 ∼ x m e^{x\ln(1+m)}-1 \sim e^{x·m}-1 \sim xm exln(1+m)−1∼ex⋅m−1∼xm
2.连续
连续:左右连续且相等,则函数连续。四则运算不影响连续性。
不连续那么中断:4类间断点。
初等函数在定义域都连续。
复合函数:
- 内外都连续,则复合函数连续;
- 内外都间断,则复合函数间断;
- 内外不一样,那么复合函数不一定。
2.1判断是否连续,不连续则判断间断点类型
把疑似间断点带进去,求极限。
2.2证明题
- 有界性定理
- 介值定理
- 最值定理
- 零点定理
二、一元函数微分学
1.导数、微分的定义
常考3种形式:
1.1导数定义求极限
f ′ ( x 0 ) = 增量 lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = Δ y Δ x = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 \begin{split} f'(x_0) &\stackrel{增量}=\lim_{\Delta x\rightarrow 0} \frac{f(x_0 + \Delta x) \color{blue}-\\ f(x_0)}{\Delta x} \\\\ &= \frac{\Delta y}{\Delta x} = \lim_{x\rightarrow x_0} \frac{f(x) \color{blue}-\\ f(x_0)}{x \color{blue}-\\ x_0} \end{split} f′(x0)=增量Δx→0limΔxf(x0+Δx)−f(x0)=ΔxΔy=x→x0limx−x0f(x)−f(x0)
特别的,当 f ( 0 ) = 0 f(0)=0 f(0)=0,则:
lim x → 0 f ( x ) x = f ′ ( 0 ) \lim_{x\rightarrow 0} \frac{f(x)}x=f'(0) x→0limxf(x)=f′(0)
求 f ′ ( x 0 ) f'(x_0) f′(x0):
lim Δ x → 0 f ( x 0 + a Δ x ) − f ( x 0 + b Δ x ) c Δ x = a − b c ⋅ f ′ ( x 0 ) \lim_{\Delta x\rightarrow0} \frac{f(x_0 + \color{red}a\\ \Delta x) \color{blue}-\\ f(x_0 + \color{red}b\\\Delta x)}{\color{red}c\\\Delta x} = \frac{a\color{blue}-\\b}c · f'(x_0) Δx→0limcΔxf(x0+aΔx)−f(x0+bΔx)=ca−b⋅f′(x0)
【技巧】
- 极限(可导)存在,那么如果 Δx→0,则 Δy→0 才可以连续。
- 如果导数在一个区间有界,那么原函数也在这个区间有界.
1.2导数定义求导数
连乘的导数,可以设后面一段有规律的连乘为 g(x).
1.3导数定义判定可导性
【频繁考点】
- 1.3.1
f ′ ( 0 ) = lim x → 0 f ( x ) − f ( 0 ) x f'(0) = \lim_{x\rightarrow 0} \frac{f(x) -f(0)}{x} f′(0)=x→0limxf(x)−f(0)
判断是否可导,就是判断这个极限是否存在.
就是看两个方向的极限是否相等:
f + ′ ( 0 ) = lim x → 0 + f ( 0 + x ) − f ( 0 ) x f − ′ ( 0 ) = lim x → 0 − f ( 0 ) − f ( 0 − x ) x f'_+(0) = \lim_{x\rightarrow 0^+} \frac{f(0+x) -f(0)}{x} \\\\ f'_-(0) = \lim_{x\rightarrow 0^-} \frac{f(0) -f(0-x)}{x} f+′(0)=x→0+limxf(0+x)−f(0)f−′(0)=x→0−limxf(0)−f(0−x)
- 1.3.2极限(可导)存在,那么如果 Δx→0,则 Δy→0 才可以连续.
判断下面这个类型是否可导:
lim x → 0 f ( ϕ ( x ) ) ψ ( x ) \lim_{x\rightarrow 0} \frac{f(\phi(x))}{\psi(x)} x→0limψ(x)f(ϕ(x))
两个条件:
- ϕ ( x ) \phi(x) ϕ(x) 要满足2点:
- ϕ ( x ) → 0 ( 是正负 0 都趋近 ) \phi(x) → 0\ (是正负0都趋近) ϕ(x)→0 (是正负0都趋近)
- ϕ ( x ) ≠ 0 \phi(x) \ne 0 ϕ(x)=0
- ϕ ( x ) \phi(x) ϕ(x) 与 ψ ( x ) \psi(x) ψ(x) 同阶.
- 1.3.3
当出现 f ( x ) = g ( x ) ∣ x − a ∣ f(x)=g(x)|x-a| f(x)=g(x)∣x−a∣ 类型,问 f ( x ) f(x) f(x) 可导?
因为左导=右导,那么 f ( a ) f(a) f(a) 可导的充要条件就是:
g ( a ) = − g ( a ) g(a)=-g(a) g(a)=−g(a),即为 g ( a ) = 0 \color{red} g(a)=0 g(a)=0.
p57
- 1.3.4
若 f ( x ) ≠ 0 f(x)\ne 0 f(x)=0,则 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣ 在 x 0 x_0 x0 可导 <=> f ( x ) f(x) f(x) 在 x 0 x_0 x0 可导.
若 f ( x ) = 0 f(x)=0 f(x)=0,则 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣ 在 x 0 x_0 x0 可导 <=> f ′ ( x ) = 0 f'(x)=0 f′(x)=0.
必须为 0,如果 f ′ ( x ) ≠ 0 f'(x)\ne 0 f′(x)=0 那么 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣ 就不可导.

2.导数几何意义
几何意义:导数 f ′ ( x 0 ) f'(x_0) f′(x0) 表示该点的斜率,切线。可导就说明有切线。
切线 f ′ ( x 0 ) f'(x_0) f′(x0): y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y-y_0 = f'(x_0)(x-x_0) y−y0=f′(x0)(x−x0)
法线 k k k:因为 切线×法线 = -1, k = − 1 f ′ ( x 0 ) k= -\cfrac1{f'(x_0)} k=−f′(x0)1
在切点处,相切的函数x, y相等,切线相等。
❗3.求导
3.1复合函数
原函数是偶函数,那导函数是奇函数;原函数是奇函数,那导函数是偶函数。
奇函数 f ′ ( 0 ) = 0 f'(0)=0 f′(0)=0.
3.2隐函数
F ( x , y ) = 0 F(x,y)=0 F(x,y)=0
有两种方法:
-
等式两边同时对自变量x求导.
【注意】这种方法,y 是关于 x 的中间变量,所以 y 也要作为复合函数求导.
【技巧】使用对数求导法简化乘除为加减形式(因为加减求导比乘除简单).
-
多元函数微分学,隐函数求导法:
【注意】这种方法,y 和 x 就是独立变量了,所以在 Fx 与 Fy 中单独求导。
d y d x = − F ′ x F ′ y \frac{dy}{dx} = -\frac{F'x}{F'y} dxdy=−F′yF′x
3.3参数方程
{ x = ϕ ( t ) y = ψ ( t ) \begin{cases} x=\phi(t)\\ y=\psi(t) \end{cases} {x=ϕ(t)y=ψ(t).一阶导:
d y d x = ψ ′ ( t ) ϕ ′ ( t ) = d y d t d x d t \frac{dy}{dx} =\frac{\psi'(t)}{\phi'(t)} =\cfrac{ \cfrac{dy}{dt} }{\cfrac{dx}{dt}} dxdy=ϕ′(t)ψ′(t)=dtdxdtdy
二阶导:
d 2 y d x 2 = d d t ⋅ ( d y d x ) ⋅ 1 d x d t \frac{d^2y}{dx^2} =\frac d{dt} ·(\frac{dy}{dx})·\cfrac{1}{\cfrac{dx}{dt}} dx2d2y=dtd⋅(dxdy)⋅dtdx1
3.4反函数
反函数 x = f − 1 ( y ) x=f^{-1}(y) x=f−1(y) 的导数 = 直接函数 y = f ( x ) y=f(x) y=f(x) 的导数的倒数。
令 x = f − 1 ( y ) = ϕ ( x ) ϕ ′ ( x ) = 1 f ′ ( x ) 令x=f^{-1}(y) = \phi(x)\\ \phi'(x) = \frac 1 {f'(x)} 令x=f−1(y)=ϕ(x)ϕ′(x)=f′(x)1
3.5对数求导法
两边同时取对数,适用于幂指函数、连乘除、开方、乘方。
3.6高阶导数
- 公式
- 归纳
- 泰勒级数
一些公式:
( u ⋅ v ) ( n ) = ∑ k = 0 n C n k ⋅ u ( k ) ⋅ v ( n − k ) ( u + v ) ( n ) = u ( n ) + v ( n ) (u·v)^{(n)}=\sum^n_{k=0}C^k_n·u^{(k)}·v^{(n-k)} \\ (u+v)^{(n)}=u^{(n)}+v^{(n)} (u⋅v)(n)=k=0∑nCnk⋅u(k)⋅v(n−k)(u+v)(n)=u(n)+v(n)
4.导数应用
-
罗尔定理
-
拉格朗日中值定理
-
柯西定理
4.1单调性、极值、最值
驻点: f ′ ( x ) = 0 f'(x)=0 f′(x)=0
f ′ ( x ) > 0 f'(x)>0 f′(x)>0,原函数单增 f ( x ) ↑ f(x)↑ f(x)↑
驻点就是临界点,极值点不一定是驻点,驻点不一定是极值点,eg. y = x 3 y=x^3 y=x3
极值点也可能是不可导点,eg. y = ∣ x ∣ y=|x| y=∣x∣
拐点: f ′ ′ ( x ) = 0 f''(x)=0 f′′(x)=0
如果驻点有二阶导数,那么:
f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0,凹函数,有极小值;
f ′ ′ ( x ) < 0 f''(x)<0 f′′(x)<0,凸函数,有极大值。
4.1.1求极值
步骤:
-
确定定义域;
-
求导找驻点、不可导点;
-
判断极大值、极小值;
-
根据左右单调性判断,可以画图。
-
根据:
f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0,凹函数,有极小值;
f ′ ′ ( x ) < 0 f''(x)<0 f′′(x)<0,凸函数,有极大值。
-
4.1.2求最值
步骤:
- 求出极值;
- 求两个端点的值;
- 比较极值和端点值。
4.2曲线凹凸性、拐点、渐近线、曲率
4.2.1渐近线
-
水平渐近线
有2条,趋近 + ∞ +∞ +∞ 和 − ∞ -∞ −∞
lim x → ∞ f ( x ) = A 水平渐近线 : y = A \lim_{x→∞}f(x)=A \\ 水平渐近线:y=A x→∞limf(x)=A水平渐近线:y=A -
垂直渐近线
lim x → x 0 f ( x ) = ∞ 垂直渐近线 : x = x 0 \lim_{x→x_0}f(x)=∞ \\ 垂直渐近线:x=x_0 x→x0limf(x)=∞垂直渐近线:x=x0 -
斜渐近线
lim x → ∞ f ( x ) x = a , lim x → ∞ ( f ( x ) − a x ) = b 斜渐近线 : y = a x + b \lim_{x→∞}\frac{f(x)}x=a\ ,\ \lim_{x→∞}(f(x)-ax)=b\\ 斜渐近线:y=ax+b x→∞limxf(x)=a , x→∞lim(f(x)−ax)=b斜渐近线:y=ax+b
【注意】水平渐近线和斜渐近线,不能共存,因为前者斜率为0,后者斜率为a.
- 步骤:
- 先看垂直渐近线。找无定义的点。
- 再看水平渐近线和斜渐近线
4.2.2曲率
-
直角坐标系 y = y ( x ) y=y(x) y=y(x).
曲率 K = ∣ y ′ ′ ∣ ( 1 + y ′ 2 ) 3 2 曲率K=\frac{|y''|}{(1+y'^2)^{\frac 32}} 曲率K=(1+y′2)23∣y′′∣ -
参数方程 { x = x ( t ) y = y ( t ) \begin{cases} x=x(t)\\ y=y(t) \end{cases} {x=x(t)y=y(t).
曲率 K = ∣ y ′ ′ x ′ − y ′ x ′ ′ ∣ ( x ′ 2 + y ′ 2 ) 3 2 曲率K=\frac{|y''x'-y'x''|}{(x'^2+y'^2)^{\frac 32}} 曲率K=(x′2+y′2)23∣y′′x′−y′x′′∣
得到曲率之后,可以求曲率半径R
曲率半径 R = 1 K 曲率半径R=\frac 1K 曲率半径R=K1
根据谁不是参数,把半径放到谁那里
e g . 通过关于 x 的方程 f ( x ) 得到 R = 1 2 曲率圆方程 : x 2 + ( y − 1 2 ) 2 = 1 4 eg.通过关于x的方程f(x)得到R=\frac12 \\ 曲率圆方程:x^2+(y-\frac12)^2=\frac14 eg.通过关于x的方程f(x)得到R=21曲率圆方程:x2+(y−21)2=41
4.3方程的根的存在性和个数
类型:
- 讨论有没有零点(根)
- 零点定理
- 罗尔定理
- 根的个数
- 单调性
- 罗尔定理推论:在区间 I I I上 f ( n ) ( x ) ≠ 0 f^{(n)}(x) \ne 0 f(n)(x)=0,则方程 f ( x ) f(x) f(x) 在该区间最多有 n 个实根。
【技巧】当有参数(例如a),把参数分离出来。p77
4.4证明:不等式
- 步骤:
- 用大的函数减去小的函数,定义为新函数
- 证明这个函数大于0成立,就是证明不等式
常用方法:
- 单调性
- 最大最小值
- 拉格朗日中值定理
- 泰勒公式
- 凹凸性
【技巧】当不等式有两个参数 a, b,那么可以把一个参数令为 x x x,把问题转化成一个未知数、一个参数的函数不等式。
4.5证明:微分中值定理
(重难点)
【技巧】
- 题干给出的条件要都用上,少用一般缺点。
- 证明在(0,1)上存在,那么如果有c∈(0, 1),那么在(0,c)上存在也可以。
4.5.1证明∃ξ∈(a,b),使得F[ξ, f(ξ), f’(ξ)]=0成立
p81
- 步骤:
- 构造辅助函数
- 分析法(还原法)
- 微分方程法:一般是解一个一阶微分方程
- 罗尔定理
另一种变式: F [ ξ , f ( ξ ) , f ′ ( ξ ) ] = 0 F[ξ, f(ξ), f'(ξ)]=0 F[ξ,f(ξ),f′(ξ)]=0 中没有导数: F [ ξ , f ( ξ ) ] = 0 F[ξ, f(ξ)]=0 F[ξ,f(ξ)]=0
- 零点定理,异号之间,存在 F ( ξ ) = 0 F(ξ)=0 F(ξ)=0.
- 拉格朗日中值定理
- 罗尔定理推论
4.5.2证明存在两个中值点η,ξ∈(a,b),使得F[ξ, f(ξ), f’(ξ), η, f(η), f’(η)]=0成立
p86
函数里面的 f ′ ( ξ ) , f ′ ( η ) f'(ξ),f'(η) f′(ξ),f′(η) 必须同时出现,才是双中值点。
- 步骤:
-
把含有的 f ′ ( ξ ) , f ′ ( η ) f'(ξ),f'(η) f′(ξ),f′(η) 分别放到两端
-
分为2种情况:
-
不要求 ξ ≠ η ξ \ne η ξ=η,在同一区间 [ a , b ] [a,b] [a,b] 中,根据两端的导数,分别使用两次中值定理:
- 拉格朗日中值定理
- 柯西中值定理
-
要求 ξ ≠ η ξ \ne η ξ=η(两个不同的点),把区间 [ a , b ] [a,b] [a,b] 分成两个子区间 [ a , ξ ] , [ ξ , b ] [a,ξ],[ξ,b] [a,ξ],[ξ,b],根据两端的导数,分别在两个子区间内使用两次拉格朗日中值定理.
其中,关键点在于 ξ ξ ξ的选取,使用“逆推法”。(介值定理)p88
-
4.5.3证明∃ξ∈(a,b),使得F[ξ, f(n)(ξ)]≥0成立
含有n阶导数。使用:
- 带拉格朗日余项的泰勒公式;
- x 0 x_0 x0 选择题目中提供函数值、导数值信息多的点。
三、一元函数积分学
1.不定积分
【注意】同一个不定积分,得到的结果不一定相同。
方法:
-
一类换元(凑微分法)
-
二类换元(去根号)
-
分部积分法:用于两类不同函数的相乘
∫ u d v = u v − ∫ v d u \int udv = uv - \int vdu ∫udv=uv−∫vdu
优先放到 d 后面的函数类型(优先级高到低):- 三指幂对反
- 其中 e x e^x ex 和三角函数一样优先
❗2.定积分
【注意】定积分 就是 常数。
方法:
-
积分中值定理(微分中值定理)p114
∫ a b f ( x ) d x = f ( ξ ) ( b − a ) = F ′ ( ξ ) ( b − a ) = F ( b ) − F ( a ) \int_a^b f(x)dx = f(ξ)(b-a) = F'(ξ)(b-a) = F(b)-F(a) ∫abf(x)dx=f(ξ)(b−a)=F′(ξ)(b−a)=F(b)−F(a)延伸:
∫ a b f ( x ) g ( x ) d x = f ( ξ ) ∫ a b g ( x ) d x \int_a^b f(x)g(x) dx = f(ξ)\int_a^b g(x)dx ∫abf(x)g(x)dx=f(ξ)∫abg(x)dx -
牛顿-莱布尼茨公式
-
换元积分法
-
分部积分法
常搭配换元。p108
-
奇偶性
∫ − a a f ( x ) d x = { 0 , f ( x ) 是奇函数 2 ∫ 0 a f ( x ) d x , f ( x ) 是偶函数 \int^a_{-a} f(x)dx= \begin{cases} 0, &f(x)是奇函数\\[2ex] 2\displaystyle \int^a_0 f(x)dx, &f(x)是偶函数 \end{cases} ∫−aaf(x)dx=⎩ ⎨ ⎧0,2∫0af(x)dx,f(x)是奇函数f(x)是偶函数 -
周期性
∫ a a + T f ( x ) d x = ∫ 0 T f ( x ) d x ∫ 0 k T f ( x ) d x = k ∫ 0 T f ( x ) d x \int_{a}^{a+T} f(x)dx= \int_{0}^{T} f(x)dx \\[2ex] \int_{0}^{kT} f(x)dx= k\int_{0}^{T} f(x)dx \\ ∫aa+Tf(x)dx=∫0Tf(x)dx∫0kTf(x)dx=k∫0Tf(x)dx -
华里士公式(点火公式)
倒计时从下面开始。
∫ 0 π 2 sin n x d x = ∫ 0 π 2 cos n x d x = { n − 1 n ⋅ n − 3 n − 2 . . . 1 2 ⋅ π 2 , n 为偶数 n − 1 n ⋅ n − 3 n − 2 . . . 2 3 ⋅ 1 , n 为大于 1 的奇数 \int_{0}^{\displaystyle\frac \pi 2} \sin^{\color{red}n} x dx= \int_{0}^{\displaystyle\frac \pi 2} \cos^{\color{red}n} x dx=\\[2ex] \begin{cases} \cfrac{n-1}n · \cfrac{n-3}{n-2}...\cfrac 12 · \cfrac {\pi}2 , & n为偶数 \\[2ex] \cfrac{n-1}n · \cfrac{n-3}{n-2}...\cfrac 23 · 1, & n为大于1的奇数 \\[2ex] \end{cases} ∫02πsinnxdx=∫02πcosnxdx=⎩ ⎨ ⎧nn−1⋅n−2n−3...21⋅2π,nn−1⋅n−2n−3...32⋅1,n为偶数n为大于1的奇数
- 其他公式
∫ 0 π f ( sin x ) d x = 2 ∫ 0 π 2 f ( sin x ) d x ∫ 0 π x f ( sin x ) d x = π 2 ∫ 0 π f ( sin x ) d x \int_{0}^{\pi} f(\sin x)dx = 2\int_{0}^{\displaystyle\frac \pi 2} f(\sin x)dx \\[2ex] \int_{0}^{\pi} {\color{red}x} f(\sin x)dx = \frac {\pi}2 \int_{0}^{\pi} f(\sin x)dx ∫0πf(sinx)dx=2∫02πf(sinx)dx∫0πxf(sinx)dx=2π∫0πf(sinx)dx
2.1定积分概念、性质、几何意义
方法:
- 积分中值定理(微分中值定理)
- 对数求导法
- 夹逼定理(放大放小)
2.2定积分计算
-
定积分几何意义
- 华里士公式
-
∫ a b f ( x ) d x = x = a + b − t ∫ a b f ( a + b − t ) d t \displaystyle \int_a^b f(x)dx \stackrel{x=a+b-t}= \int_a^b f(a+b-t)dt ∫abf(x)dx=x=a+b−t∫abf(a+b−t)dt
上下限相加,减去t。p110
-
定积分,看作常数,求导 = 0。p111
2.3变限积分
- 变上限积分求导:
[ ∫ ϕ ( x ) ψ ( x ) f ( t ) d t ] ′ = f ( ψ ) ⋅ ψ ′ ( x ) − f ( ϕ ) ⋅ ϕ ′ ( x ) [\ \int _{\phi(x)}^{\psi(x)} f(t)dt\ ]' = f(\psi)·\psi'(x)\ - \ f(\phi)·\phi'(x) [ ∫ϕ(x)ψ(x)f(t)dt ]′=f(ψ)⋅ψ′(x) − f(ϕ)⋅ϕ′(x)
- 导函数 f ( x ) f(x) f(x) 可积,原函数 ∫ f ( x ) \int f(x) ∫f(x) 连续。
- 导函数 f ( x ) f(x) f(x) 连续,原函数 ∫ f ( x ) \int f(x) ∫f(x) 可导( F ′ ( x ) = f ( x ) F'(x)=f(x) F′(x)=f(x))
- 奇偶性:进行微分、积分后,则奇偶性改变。
f ( x ) f(x) f(x) 是导函数, F ( x ) F(x) F(x) 是原函数:
- F ( x ) → f ( x ) F(x)→f(x) F(x)→f(x):
- F ( x ) F(x) F(x) 为偶, f ( x ) f(x) f(x) 为奇;
- F ( x ) F(x) F(x) 为奇, f ( x ) f(x) f(x) 为偶;
- F ( x ) F(x) F(x) 为周期, f ( x ) f(x) f(x) 为周期。
- f ( x ) → F ( x ) f(x)→F(x) f(x)→F(x):只有一个
- f ( x ) f(x) f(x) 为奇, F ( x ) F(x) F(x) 为偶。
- 导数=0,原函数是常数。
2.4积分不等式
题型:
-
比较积分大小顺序
3种方法:
- 基本不等式
- 带点进去,比较大小
- 使 x → 0 x→0 x→0,然后使用等价无穷小
-
证明不等式(难)
- 令 F ( x ) = 大的 − 小的 F(x) = 大的 - 小的 F(x)=大的−小的,即证 F ( x ) > 0 F(x)>0 F(x)>0,变成 二、4.4函数不等式。
- 变上限积分
方法:
-
定积分不等式性质
-
x x x 在 [a,b] 上有 f ( x ) ≤ g ( x ) f(x)≤g(x) f(x)≤g(x),则:
∫ a b f ( x ) d x ≤ ∫ a b g ( x ) d x \displaystyle \int_a^b f(x)dx ≤ \int_a^b g(x)dx ∫abf(x)dx≤∫abg(x)dx
-
(估值定理) f ( x ) f(x) f(x) 在 [a,b] 上连续,其中有 M , m M,m M,m 是 [a,b] 上的最大值、最小值,则:
m ( b − a ) ≤ ∫ a b f ( x ) d x ≤ M ( b − a ) m(b-a)≤ \displaystyle\int_a^b f(x)dx ≤M(b-a) m(b−a)≤∫abf(x)dx≤M(b−a)
-
∫ a b f ( x ) d x ≤ ∣ ∫ a b f ( x ) d x ∣ ≤ ∫ a b ∣ f ( x ) ∣ d x \displaystyle \int_a^b f(x)dx ≤ | \int_a^b f(x)dx| ≤ \int_a^b |f(x)|dx ∫abf(x)dx≤∣∫abf(x)dx∣≤∫ab∣f(x)∣dx
-
-
变量代换
-
积分中值定理
∫ a b f ( x ) d x = f ( ξ ) ( b − a ) \displaystyle \int_a^b f(x)dx = f(ξ)(b-a) ∫abf(x)dx=f(ξ)(b−a)
-
变上限积分(出现函数单调时常用)p121
通常会给出 f ( 0 ) = 0 f(0)=0 f(0)=0,例如证明里面有一个 ∫ 0 1 f ( x ) \int_0^1 f(x) ∫01f(x),根据积分中值定理,则:
∫ 0 x f ′ ( x ) d x = f ( x ) − f ( 0 ) f ( x ) = ∫ 0 x f ′ ( x ) d x \int_0^x f'(x)dx =f(x)-f(0) \\ f(x) = \int_0^x f'(x)dx ∫0xf′(x)dx=f(x)−f(0)f(x)=∫0xf′(x)dx -
柯西积分不等式(出现平方)p121
[ ∫ a b f ( x ) g ( x ) d x ] 2 ≤ ∫ a b f 2 ( x ) d x ⋅ ∫ a b g 2 ( x ) d x [\int_a^b f(x)\ g(x)dx]^2 ≤ \int_a^b f^2(x)dx · \int_a^bg^2(x)dx [∫abf(x) g(x)dx]2≤∫abf2(x)dx⋅∫abg2(x)dx -
基本不等式
sin x < x < tan x ( 0 < x < π 2 ) x 1 + x < ln ( 1 + x ) < x ( x > 0 ) {\color{red} \sin x<x<\tan x} (0<x<\cfrac\pi2) \\ \frac x {1+x} < \ln(1+x) < x (x>0) sinx<x<tanx(0<x<2π)1+xx<ln(1+x)<x(x>0)
3.反常积分
分为两类:
-
无穷区间上的反常积分
∫ a + ∞ f ( x ) d x = lim b → + ∞ ∫ a b f ( x ) d x \int_a^{+∞}f(x)dx = \lim_{b→+∞} \int_a^b f(x)dx \\ ∫a+∞f(x)dx=b→+∞lim∫abf(x)dx
当此时极限存在,那么收敛;若不存在(极限积分是无穷or不是常数),则发散。
∫ − ∞ + ∞ f ( x ) d x = ∫ − ∞ 0 f ( x ) d x + ∫ 0 + ∞ f ( x ) d x (3-3) \int_{-∞}^{+∞}f(x)dx = \int_{-∞}^{0}f(x)dx + \int_{0}^{+∞}f(x)dx \tag{3-3} ∫−∞+∞f(x)dx=∫−∞0f(x)dx+∫0+∞f(x)dx(3-3)
当上下限都是无穷,那么拆成两个同时都收敛,原积分才收敛。 -
无界函数的反常积
若 a 为函数的瑕点(无界点),无界函数的反常积分也称为瑕积分。
∫ a b f ( x ) d x = lim t → a ∫ t b f ( x ) d x \int_a^b f(x)dx = \lim_{t→a} \int_t^b f(x)dx \\ ∫abf(x)dx=t→alim∫tbf(x)dx
其余同 无穷区间上的反常积分 完全对应。
3.1反常积分敛散性
方法(级数):
- 比较判别法:大收小收
- 比较判别法极限形式
- P级数(无穷区间、无界函数两种不一样)
- 趋近 ∞ ∞ ∞, ∫ a + ∞ 1 x p d x \displaystyle\int_a^{+∞} \cfrac 1{x^p}dx ∫a+∞xp1dx, p > 1 p>1 p>1收敛;
- 趋近一个点, ∫ a b 1 ( x − a ) p d x \displaystyle\int_a^b \cfrac 1{(x-a)^p}dx ∫ab(x−a)p1dx, p < 1 p<1 p<1收敛。(这里x-a是趋近b,也可以b-x趋近a)
一些总结:
∫ 0 1 1 x a ( 1 − x ) b d x , a < 1 , b < 1 收敛 因为 ln x ∼ x − 1 , 除下来 , 所以下面就变成了 b − 1 ∫ 0 1 ln x x a ( 1 − x ) b d x , a < 1 , b < 2 收敛 因为 ln ( 1 − x ) ∼ x , 除下来 , 所以下面就变成了 a − 1 ∫ 0 1 ln ( 1 − x ) x a ( 1 − x ) b d x , a < 2 , b < 1 收敛 ∫ a + ∞ ln x x p d x , p > 1 收敛 \begin{split} \int_0^1 \cfrac 1{x^a(1-x)^b}dx, &\quad a<1,b<1\quad收敛 \\\\ 因为\ln x \sim x-1, 除下来, &所以下面就变成了b-1\\ \int_0^1 \cfrac {\ln x}{x^a(1-x)^b}dx, &\quad a<1,b<2\quad收敛 \\\\ 因为\ln (1-x) \sim x, 除下来, &所以下面就变成了a-1\\ \int_0^1 \cfrac {\ln (1-x)}{x^a(1-x)^b}dx, &\quad a<2,b<1\quad收敛 \\\\ \int_a^{+∞} \cfrac {\ln x}{x^p}dx,&\quad p>1\quad收敛 \end{split} ∫01xa(1−x)b1dx,因为lnx∼x−1,除下来,∫01xa(1−x)blnxdx,因为ln(1−x)∼x,除下来,∫01xa(1−x)bln(1−x)dx,∫a+∞xplnxdx,a<1,b<1收敛所以下面就变成了b−1a<1,b<2收敛所以下面就变成了a−1a<2,b<1收敛p>1收敛
【技巧】一般求极限都是一个极限,也就是积分上下有一个无界、一个有界的,但是如果上下都无界,那么就需要把它们分成两个积分极限。如公式3-3。
3.2反常积分计算
方法:
- 换元
- 分部积分
4.定积分应用
4.1求面积 S
二重积分
- 直角坐标
- 参数方程
- 极坐标
4.2求体积 V
-
旋转体 的体积 p127
-
二重积分
(p130例题3)
- 两个公式
-
微元法
-
-
已知横截面S 的体积
V = ∫ S ( x ) d x V = \int S(x)\ dx V=∫S(x) dx
4.3弧长 s
-
直角坐标
s = ∫ 1 + y ′ 2 ( x ) d x s=\int \sqrt{1+y'^2(x)}dx s=∫1+y′2(x)dx
-
参数方程
s = ∫ x ′ 2 ( t ) + y ′ 2 ( t ) d t s=\int \sqrt{x'^2(t)+y'^2(t)}dt s=∫x′2(t)+y′2(t)dt -
极坐标
s = ∫ r 2 ( θ ) + r ′ 2 ( θ ) d θ s=\int \sqrt{r^2(θ)+r'^2(θ)}dθ s=∫r2(θ)+r′2(θ)dθ
4.4旋转体的侧面积 S
S = 2 π ∫ a b f ( x ) d s 也就是 S = 2 π ∫ a b f ( x ) ( 弧长 s ) d x e . g . S = 2 π ∫ a b f ( x ) 1 + y ′ 2 ( x ) d x S=2 \pi \int_a^b f(x) ds \\ 也就是\\ S=2 \pi \int_a^b f(x) (弧长s)\ dx \\ e.g.\\ S=2 \pi \int_a^b f(x) \sqrt{1+y'^2(x)}dx S=2π∫abf(x)ds也就是S=2π∫abf(x)(弧长s) dxe.g.S=2π∫abf(x)1+y′2(x)dx
4.5物理问题
-
液体压力
压强 P = ρ g h P=ρgh P=ρgh
压强 P = 压力 F 面积 S P=\cfrac {压力F}{面积S} P=面积S压力F
-
变力沿直线所作的功
功 W = F x W=Fx W=Fx
四、常微分方程
1.微分方程
-
可分离变量的微分方程
g ( y ) d y = f ( x ) d x g(y)dy=f(x)dx g(y)dy=f(x)dx
当出现 y 2 y^2 y2 时,一般考虑可分离。 -
齐次 微分方程
y ′ = d y d x = f ( y x ) y' = \frac{dy}{dx} = f(\frac yx) y′=dxdy=f(xy) -
一阶 线性 微分方程
y ′ + P ( x ) y = Q ( x ) y'+P(x)y = Q(x) y′+P(x)y=Q(x)
【常见题型、技巧】
- 上下对调。当如 y ′ = 1 x y + y 3 y'=\cfrac 1{xy+y^3} y′=xy+y31,式子在分母。对调之后, d y d x 变 d x d y \cfrac{dy}{dx}变\cfrac{dx}{dy} dxdy变dydx,原本关于x的方程变为关于y的。
- 变量代换。当出现如 c o s ( x + y ) 或 ( x + y ) 2 cos(x+y)或\, (x+y)^2 cos(x+y)或(x+y)2,这种没法分离的,设 u = x + y u=x+y u=x+y,利用齐次微分方程的思想。
2.高阶方程降阶
令 y ′ = p y'=p y′=p
p138
3.高阶微分方程
联系:线性代数 - 线性方程组
-
二阶 常系数 齐次 微分方程
y ′ ′ + p y ′ + q y = 0 y'' + py' + qy = 0 y′′+py′+qy=0 -
二阶 常系数 非齐次 微分方程
y ′ ′ + p y ′ + q y = f ( x ) y'' + py' + qy = f(x) y′′+py′+qy=f(x)
【常见题型、技巧】p143
-
y ′ ′ + p y ′ + q y = f ( x ) y'' + py' + qy = f(x) y′′+py′+qy=f(x) 中的 f ( x ) f(x) f(x) 是有多个 P m ⋅ e λ x ⋅ sin β x P_m·e^{λx}·\sinβx Pm⋅eλx⋅sinβx,把这几部分拆开来看,最后再加起来。
-
(q4)齐次、非齐次的特解、通解:
齐次解:有多个
- 齐次解 = 非齐次特解 - 非齐次特解
- 非齐次通解 = 齐次解 + 齐次解 + 非齐次特解
- 非齐次通解 = 齐次解 + 非齐次特解
-
(q5)已知非齐次特解,求非齐次方程:
(步骤)
-
用非齐次特解,求两个齐次解,得到特征根 r;
特征方程: ( r − r 1 ) ( r − r 2 ) = 0 (r-r_1)(r-r_2)=0 (r−r1)(r−r2)=0
-
根据特征根得到齐次方程;
-
把一个非齐次特解带入齐次方程,得到 f ( x ) f(x) f(x),得到非齐次方程。
-
-
(q6)已知非齐次方程(方程给出,但又未知量)一个通解,求方程里面的未知量、非齐次方程通解:
- 分析已知的这个“一个解”,根据非齐次通解 = 齐次解 + 齐次解 + 非齐次特解,找出那个是齐次解,找出特征根 r;
- 根据特征根得到齐次方程;
- 把一个非齐次特解带入齐次方程,得到 f ( x ) f(x) f(x),得到非齐次方程;
4.综合题
4.1积分方程
题目给出一个积分方程:
-
当有积分号 ∫ \int ∫,存在式子中,使用两边同时求导,来消去积分,变成微分方程。
-
当积分不能直接求导时,考虑变量代换。
一般是 ∫ f ( u ) \int f(u) ∫f(u),但是这个u不是单个 x,这个时候就把里面内容设为 u,目的是删去 t。
-
-
求这个微分方程的通解(含有常数 C C C)。
-
然后通过上面原式子or求导过程中的式子,带入特殊点,求得通解里面的常数 C C C。
4.2函数方程
-
导数定义
f ′ ( x ) = lim f ( x + Δ x ) − f ( x ) Δ x f'(x)=\lim \cfrac {f(x+\Delta x)-f(x)}{\Delta x} f′(x)=limΔxf(x+Δx)−f(x)
-
转换成微分方程
五、多元函数微分学
- 重极限
- 连续
- 偏导数
- ❗全微分
1.重极限、连续
二重极限: lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = A \displaystyle \lim_{(x,y)→(x_0,y_0)}f(x,y)=A (x,y)→(x0,y0)limf(x,y)=A.
1.1求极限
常用的方法(原理):
- 利用极限性质(四则运算法则,夹逼原理);
- 消去分母中极限为零的因子(有理化,等价无穷小代换);
- 局部有界性
- 可以在函数中,找到一部分是有界量,那么需要求极限的就是另一部分。p151
- 无穷小量与有界变量之积仍为无穷小量
1.2证明极限不存在
二重极限 : lim ( x , y ) → ( x 0 , y 0 ) x p ⋅ y q x m + y n 二重极限:\lim_{(x,y)→(x_0,y_0)} \frac{x^p·y^q}{x^m+y^n} 二重极限:(x,y)→(x0,y0)limxm+ynxp⋅yq
- m、n 不全是偶数,极限不存在。
- 计算 p m + q n \cfrac pm + \cfrac qn mp+nq
- p m + q n > 1 \cfrac pm + \cfrac qn >1 mp+nq>1,则极限 = 0.
- p m + q n ≤ 1 \cfrac pm + \cfrac qn ≤1 mp+nq≤1,则极限不存在.
2.偏导数、全微分
2.1偏导数
2.1.1偏导数定义
某一点偏导存在:左右导存在且相等
lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = lim Δ x → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) Δ y \lim_{Δx→0} \frac {f(x_0+Δx, y_0) - f(x_0, y_0)}{Δx} \\ =\lim_{Δx→0} \frac {f(x_0, y_0+Δy) - f(x_0, y_0)}{Δy} Δx→0limΔxf(x0+Δx,y0)−f(x0,y0)=Δx→0limΔyf(x0,y0+Δy)−f(x0,y0)
【计算技巧】先代后算
先代后求:实际求偏导数时候,通常给出两个变量,然后求一个偏导。那么就可以把不是所求偏导的那个变量先代进去再求,如求 x的偏导 f x ( 0 , 1 ) f_x(0,1) fx(0,1),可以先把y的值代进去:
∂ f ∂ x = f x ′ ( 0 , 1 ) = d d x [ f ( x , 1 ) ] ∣ x = 0 \frac{∂f}{∂x} = f'_x(0,1) = \frac d{dx} [f(x,1)] |_{x=0} ∂x∂f=fx′(0,1)=dxd[f(x,1)]∣x=0
2.1.2高阶偏导数
如对 x 求两次偏导:
∂ ∂ x ( ∂ z ∂ x ) = ∂ 2 z ∂ x 2 = f x x ( x , y ) \frac{∂}{∂x}(\frac{∂z}{∂x}) = \frac{∂^2z}{∂x^2} = f_{xx}(x,y) ∂x∂(∂x∂z)=∂x2∂2z=fxx(x,y)
- 顺序很重要
如:先对x求导,再对y求导。那么合并起来写就是 ∂ x ∂ y ∂x∂y ∂x∂y,是从左到右依次的。
∂ ∂ y ( ∂ z ∂ x ) = ∂ 2 z ∂ x ∂ y = f x y ( x , y ) \frac{∂}{∂y}(\frac{∂z}{∂x}) = \frac{∂^2z}{∂x∂y} = f_{xy}(x,y) ∂y∂(∂x∂z)=∂x∂y∂2z=fxy(x,y)
2.2.全微分
2.2.1全微分判断
全微分存在的条件:
- f x 、 f y f_x、f_y fx、fy两个偏导存在;
- f x 、 f y f_x、f_y fx、fy两个偏导在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)连续;
- 可以使用重极限:p155
lim ( Δ x , Δ y ) → ( x 0 , y 0 ) Δ z − f x ′ Δ x − f y ′ Δ y ( Δ x ) 2 + ( Δ y ) 2 = 0 \lim_{(Δx,Δy)→(x_0,y_0)} \frac {Δz - f'_xΔx - f'_yΔy} {\sqrt{(Δx)^2+(Δy)^2}} =0 (Δx,Δy)→(x0,y0)lim(Δx)2+(Δy)2Δz−fx′Δx−fy′Δy=0
Δz 则是 z 的变化量,即全增量: d z = f ( x + Δ x , y + Δ y ) − f ( x , y ) dz= f(x+Δx, y+ Δy)-f(x,y) dz=f(x+Δx,y+Δy)−f(x,y).
lim ( Δ x , Δ y ) → ( x 0 , y 0 ) f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) − f x ′ Δ x − f y ′ Δ y ( Δ x ) 2 + ( Δ y ) 2 = 0 \lim_{(Δx,Δy)→(x_0,y_0)} \frac {f(x_0+Δx, y_0+Δy)-f(x_0,y_0) - f'_xΔx - f'_yΔy} {\sqrt{(Δx)^2+(Δy)^2}} =0 (Δx,Δy)→(x0,y0)lim(Δx)2+(Δy)2f(x0+Δx,y0+Δy)−f(x0,y0)−fx′Δx−fy′Δy=0
2.2.1全微分计算
d z = ∂ z ∂ x d x + ∂ z ∂ y d y dz = \frac {∂z}{∂x}dx + \frac{∂z}{∂y}dy dz=∂x∂zdx+∂y∂zdy
2.3复合函数
-
复合函数求导法 u、v
d z d x = ∂ z ∂ u d u d x + ∂ z ∂ v d v d x \frac {dz}{dx} = \frac {∂z}{∂u} \frac {du}{dx} + \frac{∂z}{∂v}\frac {dv}{dx} dxdz=∂u∂zdxdu+∂v∂zdxdv -
全微分形式的不变性
d z = ∂ z ∂ x d x + ∂ z ∂ y d y = ∂ z ∂ u d u + ∂ z ∂ v d v dz = \frac{∂z}{∂x}dx + \frac{∂z}{∂y}dy \\ =\frac{∂z}{∂u}du + \frac{∂z}{∂v}dv dz=∂x∂zdx+∂y∂zdy=∂u∂zdu+∂v∂zdv -
复合函数二阶微分
2.4隐函数
隐函数求导的方法:
-
公式:隐函数 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0:( F x ′ F'_x Fx′ 是指关于 x 的偏导)
d y d x = − F x ′ F y ′ \frac{dy}{dx} = - \frac{F'_x}{F'_y} dxdy=−Fy′Fx′ -
微分形式不变性:
- 在 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0 下:
F x ′ d x + F y ′ d y + F z ′ d z = 0 F'_xdx + F'_ydy + F'_zdz = 0 Fx′dx+Fy′dy+Fz′dz=0
- 在 F ( x , y , z ) = u F(x,y,z)=u F(x,y,z)=u 下:
∂ F ∂ x d x + ∂ F ∂ y d y + ∂ F ∂ z d z = d u \frac{∂F}{∂x}dx + \frac{∂F}{∂y}dy + \frac{∂F}{∂z}dz = du ∂x∂Fdx+∂y∂Fdy+∂z∂Fdz=du
-
(取对数)等式两边同时求导
题型(求偏导数与全微分)
1)求一点处的偏导数与全微分
- 分段函数的分界点,偏导一般用定义;
- 先代后求。
2)求已给出具体表达式函数的偏导数与全微分
- 复合函数求偏导法
- 已知偏导逆运算(倒退回)表达式 p161
3)含有抽象函数的复合函数的偏导数与全微分
-
抽象复合 f ( f 1 , f 2 ) f(f_1,f_2) f(f1,f2) 的导数:
【注意】题干中有时候也会给出 fx 就是 f1,fy 就是 f2
d f = f 1 ′ ⋅ ( f 1 里面的函数的关于变量的导数 ) + f 2 ′ ⋅ ( f 2 里面的函数的关于变量的导数 ) df = f_1'·(f_1里面的函数的关于变量的导数) + f_2'·(f_2里面的函数的关于变量的导数) df=f1′⋅(f1里面的函数的关于变量的导数)+f2′⋅(f2里面的函数的关于变量的导数)
-
例1: d f ( x + 1 , e x ) = f 1 ′ ( x + 1 , e x ) + f 2 ′ ( x + 1 , e x ) e x df(x+1,e^x) = f_1'(x+1,e^x)+f_2'(x+1,e^x)e^x df(x+1,ex)=f1′(x+1,ex)+f2′(x+1,ex)ex,或者简写: d f ( x + 1 , e x ) = f 1 ′ + e x f 2 ′ df(x+1,e^x) = f_1'+e^xf_2' df(x+1,ex)=f1′+exf2′.
-
例2: f ( y x , x 2 + y 2 ) f(yx,x^2+y^2) f(yx,x2+y2) 的:
∂ z ∂ x = y f 1 ′ + 2 x f 2 ′ \displaystyle \frac{∂z}{∂x}= yf_1'+2xf_2' ∂x∂z=yf1′+2xf2′.
-
复合函数二阶微分:可以把 y f 1 ′ yf_1' yf1′ 再看作一个复合函数,而其中的 f 1 ′ f_1' f1′也是一个 f 1 ′ ( y x , x 2 + y 2 ) f_1'(yx,x^2+y^2) f1′(yx,x2+y2),所以:
∂ 2 z ∂ x ∂ y = f 1 ′ + y ( x f 11 ′ ′ + 2 y f 12 ′ ′ ) + 2 x ( x f 21 ′ ′ + 2 y f 22 ′ ′ ) \displaystyle \frac{∂^2z}{∂x∂y}= f_1'+y(xf_{11}''+2yf_{12}'') + 2x(xf_{21}''+2yf_{22}'') ∂x∂y∂2z=f1′+y(xf11′′+2yf12′′)+2x(xf21′′+2yf22′′).
-
- 当遇到要求的二阶偏导是其他非x,y变量,那么直奔主题求目标。p166
4)隐函数的偏导数与全微分
隐函数求导看2.4
-
当给出多个抽象函数关系,然后求一个偏导(且函数之间变量关系不好找清楚),可以使用微分形式不变性。p170
步骤:
- 把给出的函数关系转换成全微分形式;
- 消去不需要的变量。OK
4.极值、最值
多元函数极值、最值
4.1求无条件极值
无条件极值就对应一元函数的极值。
步骤:
- 确定定义域;
- 求导找驻点,偏导数为0: { ∂ z ∂ x = 0 ∂ z ∂ y = 0 \begin{cases} \cfrac{∂z}{∂x}=0 \\[1em] \cfrac{∂z}{∂y}=0 \end{cases} ⎩ ⎨ ⎧∂x∂z=0∂y∂z=0,得到可能多个驻点的(x0,y0)。
- 把(x0,y0)带入二次偏导,判断极大值、极小值。
令 f x x ′ ′ = A f_{xx}''=A fxx′′=A,
f x y ′ ′ = f y x ′ ′ = B f_{xy}''=f_{yx}''=B fxy′′=fyx′′=B,
f y y ′ ′ = C f_{yy}''=C fyy′′=C,
- AC - B2 > 0:有极值,A > 0:是极小值;A < 0:是极大值。(A>0开口向上)
- AC - B2 < 0:无极值;
- AC - B2 = 0:不一定,需要讨论。
- 隐函数求导,当偏导数式子里面有多个变量,先令其他变量为0或者什么值,求出x,y,然后把x,y代回原方程,得到z(可能有多个z)。p174
4.2条件最值(拉格朗日乘数法)
求最大最小值
- 只有x,y两个变量,可以使用线性代数求解拉格朗日函数。
- 目标函数简化。p179
- 画图找几何解法,例如是一个圆。
六、二重积分
1.计算二重积分
-
直角坐标
-
极坐标(圆)
-
奇偶性 p183
-
x是奇,看区域D是否关于y轴对称,是则D=0;
-
y是奇,看区域D是否关于x轴对称,是则D=0。
-
奇偶性的平移
p187方法三、p188方法三
-
-
变量对称性:D关于 y = x y=x y=x 对称。
p184
-
y 和 x 可以对调
-
适合简化极坐标,然后在使用极坐标
-
【技巧】
- 画辅助线,分成多个区域,利用奇偶性,使得积分=0.
- 当极坐标圆心(a,b)不在xy坐标轴上,考虑使用新的 { x − a = r cos θ y − b = r sin θ \begin{cases} x-a=r\cos θ \\[0.5em] y-b=r\sin θ \end{cases} ⎩ ⎨ ⎧x−a=rcosθy−b=rsinθ.
【特殊考点】
- 摆线
2.累次积分:交换次序&计算
就是画出图形,看图形的特点,分区域求积分然后加和。
3.综合、证明
技巧:
- 先积分x,还是先积分y,可以交换顺序。
相关文章:

【考研数学 - 数二题型】考研数学必吃榜(数二)
数学二 suhan, 2024.10 文章目录 数学二一、函数❗1.极限1.1求常见极限1.2求数列极限1.2.1 n项和数列极限1.2.2 n项连乘数列极限1.2.3 递推关系定义的数列极限 1.3确定极限式中的参数1.4无穷小量阶的比较 2.连续2.1判断是否连续,不连续则判断间断点类型2.2证明题 二…...

Redis生产问题(缓存穿透、击穿、雪崩)——针对实习面试
目录 Redis生产问题什么是缓存穿透?如何解决缓存穿透?什么是缓存击穿?如何解决缓存击穿?缓存穿透和缓存击穿有什么区别?什么是缓存雪崩?如何解决缓存雪崩? Redis生产问题 什么是缓存穿透&#x…...

android openGL中模板测试、深度测试功能的先后顺序
目录 一、顺序 二、模板测试 1、概念 2、工作原理 3、关键函数 三、深度测试 1、概念 2、工作原理 3、关键函数 三、模板测试和深度测试的先后顺序 一、顺序 在Android OpenGL中,模板测试(Stencil Testing)是在深度测试࿰…...

CCF PTA 编程培训师资认证2021年7月真题- C++兑换礼品
【题目描述】 小零和小壹是两个爱玩游戏的小孩,他俩平时最擅长的是解谜游戏,可今天 遇到了一个有点难的算法问题,希望能得到你的帮助。 他们面对的是一个电子装置,正面有 n 个排成一列的按钮,按钮上贴着编号 1~n 号的…...

火山引擎云服务docker 安装
安装 Docker 登录云服务器。 执行以下命令,添加 yum 源。 yum update -y yum install epel-release -y yum clean all yum list依次执行以下命令,添加Docker CE镜像源。更多操作请参考Docker CE镜像。 # 安装必要的一些系统工具 sudo yum install -y yu…...

【taro react】 ---- 常用自定义 React Hooks 的实现【六】之类渐入动画效果的轮播
1. 效果 2. 场景 css 效果实现:可以看到效果图中就是一个图片从小到大的切换动画效果,这个效果很简单,使用 css 的 transform 的 scale 来实现图片的从小到大的效果,切换就更加简单了,不管是 opacity 还是 visibility 都可以实现图片的隐藏和显示的切换。React.Children.m…...

基础算法练习--滑动窗口(已完结)
算法介绍 滑动窗口算法来自tcp协议的一种特性,它的高效使得其也变成了算法题的一种重要考点.滑动窗口的实现实际上也是通过两个指针前后遍历集合实现,但是因为它有固定的解题格式,我将其单独做成一个篇章. 滑动窗口的解题格式: 首先,定义两个指针left和right,与双指针不同的…...

深度学习经典模型之ZFNet
1 ZFNet 1.1 模型介绍 ZFNet是由 M a t t h e w Matthew Matthew D . Z e i l e r D. Zeiler D.Zeiler和 R o b Rob Rob F e r g u s Fergus Fergus在AlexNet基础上提出的大型卷积网络,在2013年ILSVRC图像分类竞赛中以11.19%的错误率获得冠军(实际…...

Linux系统-ubuntu系统安装
作者介绍:简历上没有一个精通的运维工程师。希望大家多多关注作者,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 这是Linux进阶部分的最后一大章。讲完这一章以后,我们Linux进阶部分讲完以后,我们的Linux操作部分就…...

2-Ubuntu/Windows系统启动盘制作
学习目标: 掌握使用Win32DiskImager、Rufus等工具制作系统启动盘的基本步骤。独立将ISO镜像文件写入USB闪存驱动器,确保在需要时顺利安装或修复系统。通过学习如何选择正确的源文件和目标驱动器,理解启动盘的使用场景和注意事项,…...

你使用过哪些MySQL中复杂且使用不频繁的函数?
在MySQL中,除了常用的SELECT、INSERT、UPDATE等基本操作外,还有许多复杂且功能强大的函数,它们能够处理各种复杂的数据处理需求。这些函数虽然在日常开发中可能不常使用,但在特定场景下却能够发挥巨大的作用。下面,我将…...

Redis-07 Redis哨兵
操作实现 此处应该6台虚拟机,其中3台是哨兵,但因为内存限制没有那么多 1.将sentinel文件拷贝到/myredis目录下 2.sentinel.conf文件重要参数 新建配置文件sentinel26379.conf sentinel26380.conf sentinel26381.conf bind 0.0.0.0 daemonize yes pr…...
7.qsqlquerymodel 与 qtableview使用
目录 qtableview 委托QStyledItemDelegateQAbstractItemDelegateCheckBoxItemDelegate使用qtableview控制列宽,行高,隐藏拖拽行列 qtableview 委托 //设置单元格委托 void setItemDelegate(QAbstractItemDelegate *delegate); QAbstractItemDelegate *it…...
详解)
状态模式(State Pattern)详解
1. 引言 在很多软件系统中,对象的行为往往依赖于其内部状态,而状态的变化又会影响对象的行为。状态模式(State Pattern)为解决这一问题提供了一种优雅的方法。通过将状态的行为封装到独立的状态对象中,可以使得对象在…...

ajax微信静默登录不起效不跳转问题
问题描述: 今天通过ajax调用方式做微信静默登录,发现本地可以跳转,到线上地址死活都不跳转,就像没起作用一般,经许久排查发现,是因为https和http域名的问题,线上只配置了http域名࿰…...
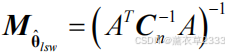
参数估计理论
估计理论的主要任务是在某种信号假设下,估算该信号中某个参数(比如幅度、相位、达到时间)的具体取值。 参数估计:先假定研究的问题具有某种数学模型, 如正态分布,二项分布,再用已知类别的学习样…...

mybatis插入数据运行成功但数据库没有数据,id却在增长,是什么原因??
错误描述: mybatis插入数据运行成功,但是数据库却没有数据,id也在增加 原因:在测试方法上面加了 Transactional 虽然日志显示插入语句执行成功,但可能事务在提交过程中出现了问题。比如在后续的操作中有异常抛出导…...

Hadoop简介及单点伪分布式安装
目录 1. 大数据2. Hadoop简介3. Hadoop伪分布式安装4. Hadoop启动参考 1. 大数据 大数据的定义:一种规模大到在获取、存储、管理、分析方面大大超出传统数据库软件工具能力范围的数据集合。 特征: 1.海量的数据规模 2.快速的数据流转 3.…...

网站架构知识之Ansible模块(day021)
1.Ansible模块 作用:通过ansible模块实现批量管理 2.command模块与shell模块 command模块是ansible默认的模块,适用于执行简单的命令,不支持特殊符号 案列01,批量获取主机名 ansible all -m command -a hostname all表示对主机清单所有组…...

是时候用开源降低AI落地门槛了
过去三十多年,从Linux到KVM,从OpenStack到Kubernetes,IT领域众多关键技术都来自开源。开源技术不仅大幅降低了IT成本,也降低了企业技术创新的门槛。 那么,在生成式AI时代,开源能够为AI带来什么?…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
